高速铁路列车运行调整优化模型研究

蔡 涛

CAI Tao

（中国铁道科学研究院 通信信号研究所，北京 100081）

(Communication and Signaling Research Institute， China Academy of Railway Sciences， Beijing 100081， China)

高速铁路列车运行调整优化模型研究

蔡 涛

CAI Tao

（中国铁道科学研究院 通信信号研究所，北京 100081）

(Communication and Signaling Research Institute， China Academy of Railway Sciences， Beijing 100081， China)

在阐述铁路列车运行调整研究现状的基础上，针对日常列车运行调整问题，根据高速铁路列车运行资源占用的特点，为每列列车赋予 1 个价值，以整体价值最大化为优化目标，建立基于时空网络资源占用的数学模型，并运用改进拉格朗日松弛算法对该模型进行化简求解，以京沪高速铁路进行实例分析，结果表明该算法能够满足实际应用的需要。

运行计划；价值函数；拉格朗日松弛；最优化

铁路运输调度是指为使运输生产控制在正常状态，根据具体运输工作条件调整车辆分布及列车运行，以解决可能或发生的困难。调度实践证明，调度指挥的主要问题是在列车不按图运行时，根据列车和设备的状态快速进行最优决策[1]；在区段通过能力使用紧张和高速行车的条件下，通常还需要对临近区段进行考虑，增加列车调度员进行最优决策的困难。因此，如何有效利用现有的线路资源，快速找到全局最优或较优高速铁路行车调整方案，是铁路运输组织管理和优化研究领域亟需解决的问题[1]。在国内研究中，许红等[2]将列车分为 A类本线列车、B 类跨线列车和 C 类本线城际列车分别进行建模，并采用遗传算法进行求解。谢美全等[3]结合我国客运专线的实际情况，针对运营情况复杂的线路提出基于定序的周期性列车运行图模型。汪波等[4]等将安排列车运行线的问题看作周期事件安排问题，借助周期约束图及周期势差模型，建立周期运行图网络模型。在国外研究中，XIE M 等[5]主要讨论高速铁路运行图调整问题，提出在发到时间确定情况下的整数线性规划模型，以优化循环动车组。Vansteenwegen P 等[6]考虑实时调度环境下的随机扰动，基于列车不确定的运行时间及制订中期时刻表过程中的调度原则问题，提出随机优化模型。由于拉格朗日松弛算法 (Lagrangian Relaxation) 已经在许多实际工程问题的研究中得到应用，虽然其对模型的构建和算法设计要求严格，但拥有优秀的鲁棒性和高效性特点，可以求解大规模的线性规划问题，并且能给出明确的对偶间隙用于评价当前解的质量，因而仍然考虑将拉格朗日松弛算法用于求解日常列车运行调整问题，并且以京沪高速铁路 (以下简称“京沪高铁”) 实际数据为背景进行案例研究，对其适用性、可靠性进行验证。

1　列车运行计划编制模型的构建

1.1问题描述

列车运行计划编制问题可以通过时空网络进行说明，如图 1 所示。纵轴为时间，考虑将连续的时间离散化，形成 1 个列车时刻表。在我国铁路系统中，时刻表通常以 1 min 为最小单位，横轴表示资源 (车站和区间)。当安排 1 列列车从始发站发出，根据基本列车运行图可以得到列车的最佳发车时间范围，称这个时间段是该列车在该车站的允许发车时间范围。允许发车时间范围越长，列车出发时间的选择越多。

图1　运行计划编制问题说明

在图 1 中，假设列车 j 在每个车站的允许发车时间范围均为 α min，如果时刻表以 1 min 为最小时间单位，那么列车 j 在每个车站的可选发车时间有 α 个，列车 j 到达终到站需要通过 β 个车站，可以编制出列车 j 的所有可行行车方案。列车 j 从始发站开始允许发车时间范围为 α min，以此类推，最终列车 j 的可行方案有 αβ个。随着列车数量和车站数量的增加，变量和约束的数量呈指数增长，那么优化路网中列车运行计划将会在一个指数级增长的搜索空间内寻找最优解。

RT 是指列车在相邻 2 个站间的纯运行时间，对于 1 列列车，RT 是 1 个定值，TT 是旅行时间，包括列车启停时间和停站时间，一旦列车停站，则产生启停车附加时分，为建模方便，将启停车附加时间和停站时间合并，如图 1 中的 ST。因此，列车经过途中车站有 2 种选择：①列车在途经车站不停车(RT)；②由于运行计划或其他约束的影响，列车需要在中途车站停车作业 (TT)。

在时空网络中，如果同时考虑 2 列或 2 列以上的列车，列车之间会出现冲突，一旦发生冲突，就需要调整列车的发车时间和占用股道时间。考虑将区间、车站股道作为列车竞争的资源，并且对每个资源在每个时间点赋予 1 个价格，那么不同的运行计划就会花费不同的资源和费用，当多个列车之间出现冲突时，可以通过改变在冲突时间点的资源价格来对多个列车的占用进行排序。在迭代过程中，通过更新资源价格矩阵，找到列车由始发站到终到站利润最大的路径。每列车的利润为列车收益减去列车在运行途中占用资源的成本，从而构建列车运行计划编制模型。

1.2模型构建

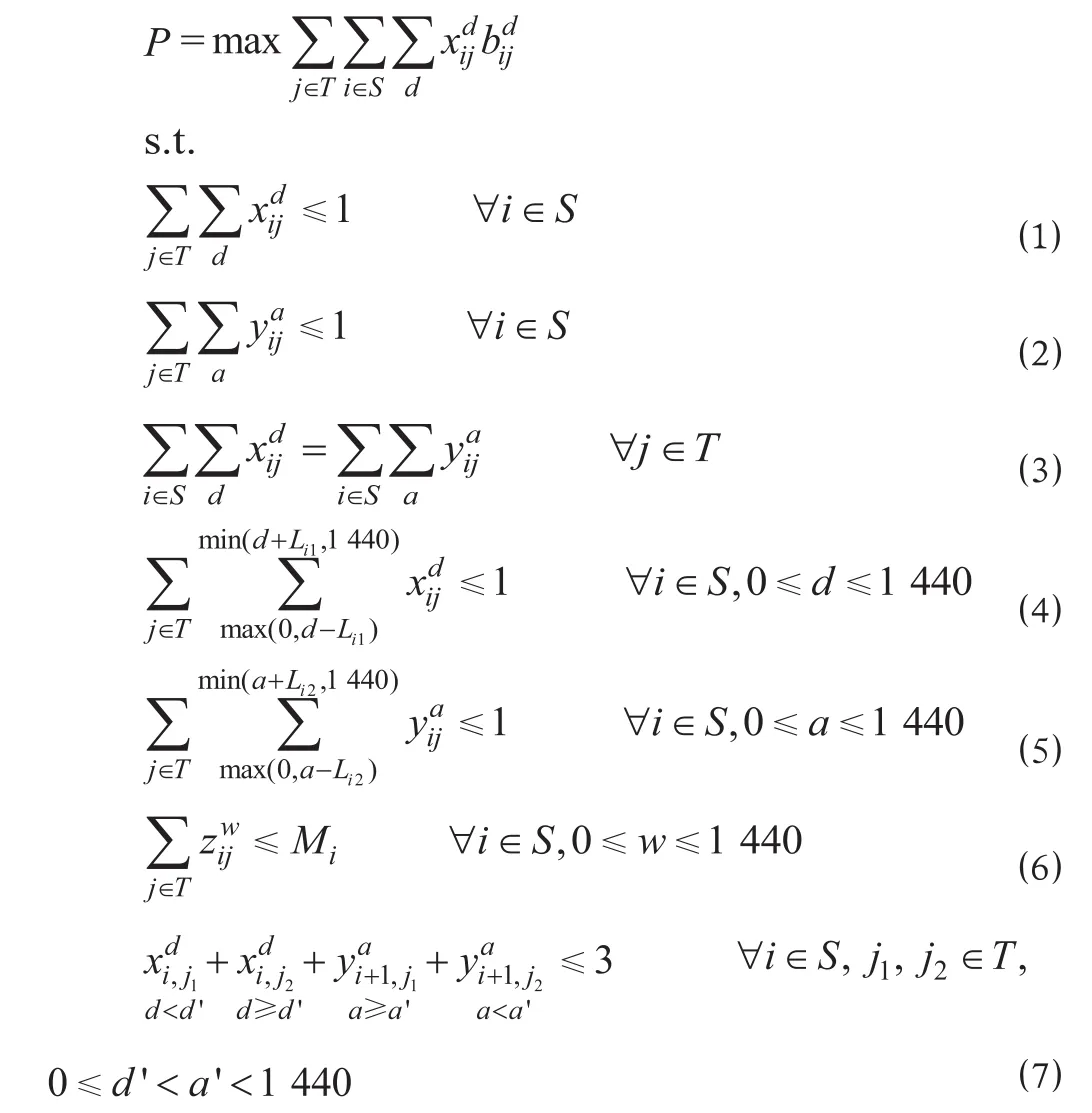
式中：P 为优化目标函数，即所有列车在各个车站的发车时间价值最大，通过运行图铺画实现所有移动设备、固定设备及人工投入能够取得最大化利益；j 为列车，j ∈ T，T 包含所有可能被铺画上运行图列车的集合，列车分为 2 个等级，分别用集合G，D 表示；i 为车站，i ∈ S，S 为线路沿线的所有车站的集合；设 dij为列车 j ( j ∈ T ) 在 i ( fi≤i≤lj) 站的发车时刻，d ∈ D，0 ≤d≤1 440，为对应于 dij的 0-1 决策变量，当且仅当时间点 dij(0 ≤dij＜1 440， d ∈ Di， j ∈ T，fi≤i ＜lj) 被选作最优解时，值为1；bij为列车 j 在车站 i 发车的价值；设 aij为列车j ( j ∈ T ) 在 i ( fi＜i≤lj) 站的到达时刻，a ∈ A，0 ≤a≤ 1 440，为对应于 aij的 0-1 决策变量，当且仅当时 间点 aij(0 ≤aij≤1 440，a ∈ Ai，j ∈ T，fi≤i≤lj) 被选作最优解时，值为 1；Li1为车站 i 的最小发车间隔时间；Li2为车站 i 的最小接车间隔时间；设 wij为列车 j ( j ∈ T ) 在 i ( fi≤i≤lj) 站的等待时刻，w ∈ W， 0 ≤w≤1 400，zwij为对应于 wij的 0-1 决策变量，当且仅当时间点 wij(0 ≤wij＜1 440，w ∈ Wi，j ∈ T， fi≤i ＜lj) 被选作最优解时，的值为 1；Mi为车站 i 的股道限制； j1为在 i 站于时间点 d 之前发车的某趟列车； j2为在 i 站于时间点 d 之后发车的某趟列车。

⑴ 式表示同一车站相同方向的发车时间点最多只能被占用 1 次；⑵ 式表示同车站同方向的接车时间点最多只能被占用 1 次；⑶ 式表示每趟列车的发车时刻数与到达时刻数相等，即保证运行线的连续性；⑷ 式表示最小发车间隔约束；⑸ 式表示最小接车间隔约束；⑹ 式表示车站股道占用限制，同一车站同一时间不可停留过多列车；⑺ 式表示区间资源占用约束，即列车在区间内不得越行。

dij，aij，wij及 0-1 变量之间的关系如下。

式中：j ∈ T ，fi＜i≤lj，Ri,i+1为列车 j 在 i 站与 i +1 站之间站间区间的运行时间标尺；如果 dij对应的变量xd= 1，则对应于满足 ⑻ 式中 a 的变量

iji+1,j，表示列车 j 于 ai+1,j时刻到达 i + 1 站。

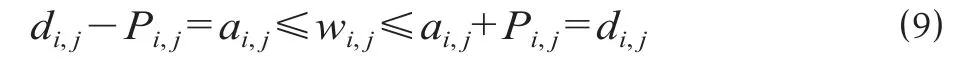
式中：j ∈ T ，fi＜i≤lj，Pi,j为列车 j 在 i 站的停车时间标准，即如果 dij对应的变量= 1，则对应于满足 ⑼ 式的 wi,j变量 zwij= 1，表示列车 j 于 wi,j时刻占用 i 站股道。

每一趟列车在所有途经车站 (终到站除外) 都有1 个最佳发车时间 (图定发车时刻)，该发车时刻带来的效益最大，其价值也最大，表示时间点 dij发车的价值，越偏离最佳发车时间价值衰减越大。各时间点的价值既可以通过人为合理定义，也可以按照某一函数曲线确定。通过线性价格函数来确定不同发车时间的价值，如图 2 所示，为在图定时刻发车能获得最大效益，α1为早点范围，α2为晚点范围。

该模型的构建基础为在已有线路条件下，股道运用方案为已知。因此，同一时间站内能够停靠的列车数有限。中间站需要为列车运行提供停车避让的股道，如果某车站 i 上行有 h 条专用股道，下行有 g 条专用股道，同时有 r (r≥0) 条上下行共用的股道，则上行股道限制为 Mis= h + r，下行为 Mix= g + r；如果上行股道被占用数 Cs= h + p (0 ≤p≤r)，下行股道被占用数 Cx≤g，则上行限制仍然为 Mis= h + r，下行限制变为 Mix= h + r - p，反之亦然；如果上行股道被占用数为 Cs= h + p ，下行股道被占用数为 Cx= g + q，0 ≤p + q≤r，则上行限制变为 Mis= h + r - q，下行限制变为 Mix= g + r - p。

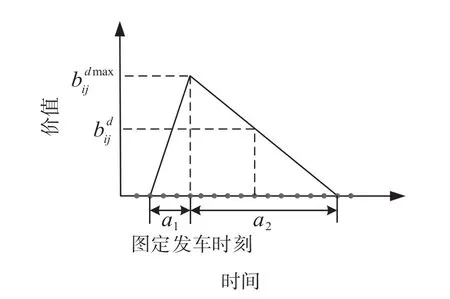
图2　时间价值函数线

2　基于拉格朗日算法的模型求解过程

该模型的约束条件多而复杂，求解比较困难。模型包含 3 种变量，总变量数计算公式为Nv= 3 |T |×|S |，约束条件个数计算公式为 Nc= 2 |S | + |T | + 3×1 440×|S | + |S |×|T |2×1 440。对京沪高铁的实际案例而言，如果对于 23 个车站，100 对列车进行调整优化，变量将达到 1.4 万个，约束达到3.3亿个，直接精确求解该问题有一定难度。

2.1拉格朗日松弛算法

拉格朗日松弛算法是一种分解协调算法，具有可以快速收敛到可行解，震荡收敛到最优解的特点[7]。拉格朗日乘子可以看作是每个车站在某时刻发车的时间占用价格。基于拉格朗日松弛理论，如果将约束松弛，可以将原问题变成不考虑列车之间相互影响的若干个子问题。松弛约束条件 ⑷ 式至⑹ 式为拉格朗日松弛问题，给定 1 组非负的拉格朗日乘子，则高速铁路运行计划编制问题的拉格朗日松弛问题记为 PL，则

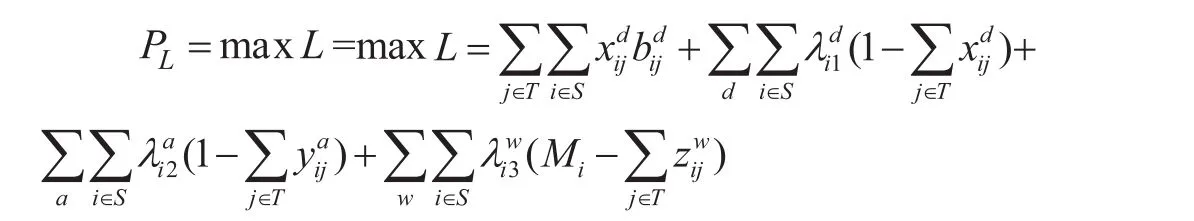
为简化问题求解，可以设 PLD为 PL的拉格朗日对偶问题，计算公式为

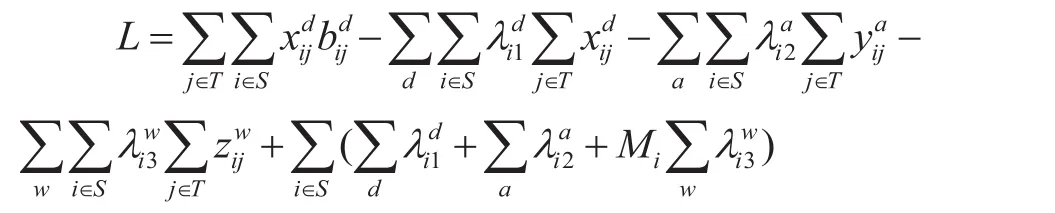
进一步简化得到

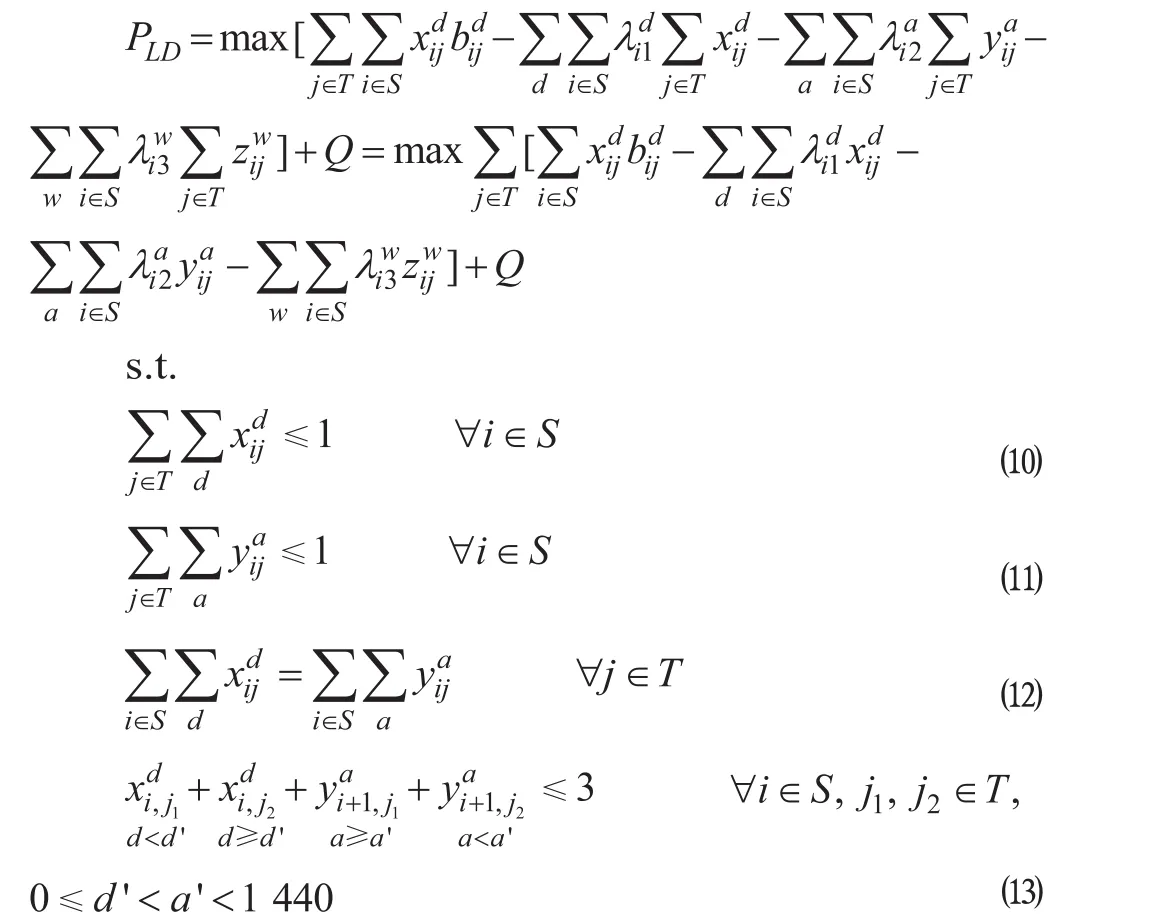
式中：每一个子问题 qj表示 1 次列车的最优调整方案，此时未考虑列车之间的相互影响，具体物理含义是该列车的价值减去占用各资源的费用，各资源的占用费用即为各拉格朗日乘子的取值；Q 表示仅与拉格朗日乘子相关而与决策变量无关的数值，在每一步迭代过程中，拉格朗日乘子通过算法先确定下来，此时 Q 值是 1 个定值，如果每个子问题均能取得最优值，即得到最优解。通过多次迭代改变拉格朗日乘子的取值，理论上当拉格朗日乘子固定下来，即资源占用的费用平稳时系统达到最优状态。

2.2模型求解

在列车的站间区间运行标尺确定的情况下，按照约束条件 ⑽ 式至⒀ 式，将所有列车在可调整范围内的所有可行解列出，并计算其总价值 PLD，从中找出目标值最优方案。

对于模型 PL= max L，在每次迭代中，拉格朗日乘子都被更新。依据实际问题的特性，还可以选取特定节点来简化问题。①节点选择原则。根据我国高速铁路的特点，选择一些枢纽站、其他线路(支线)接入站作为节点，只有被选为节点的车站才能作为列车的始发站或终到站。②分支、剪枝。为减少工作量，可以利用目标函数值进行剪枝。③搜索最优解。每两个节点之间的线路都得到 1 个最优解，通过搜索始发站到终到站的最优路径，形成 1个完整的列车运行调整方案，最终得到 1 个子问题的解。

2.3算法步骤

运用拉格朗日松弛算法，松弛掉列车之间的影响约束，从而将求多次列车的整体最优调整方案的复杂问题转变为求每一次列车的最优调整方案。算法的具体步骤如下。

步骤 1：初始化。将时间间隔设为 1 min，即 1天有 1 440 个时刻可供选择。迭代次数 n = 0。建立1 440×S 阶 0 矩阵 λ1440×S，其中元素 λm×S为m (0≤m ＜1 440) 时刻从 i (1≤i ＜s) 车站发车所对应的拉格朗日乘子。建立 t (列车数) 个 1 440×(lj－ fj+ 1) 阶 0 矩阵，分别表示为列车 j ( j ∈ T)在 i (i ∈ S) 车站所安排的发车时刻、到达时刻和停车时刻。设定价值参数 B、轨道限制参数 Mi、步长调节因子 γ0。

步骤 2：安排高等级列车在各站的发车时间。高等级列车无需避让，可以按照各自最佳发车时间运行。用矩阵记录列车的发车时刻，并且通过区间运行标尺及中间站停站时间推算到站时刻矩阵和停站时间矩阵，重复该步骤直至高等级列车完成安排。

步骤 3：安排低等级列车。低等级列车往往需要在中间站停车避让，通常不能按照最佳发车时间发车，用分支定界方法在最佳发车时间邻域搜寻利益最大点 (较之最佳发车时间其价值次之、负影响小) 作为实际发车时间，并用矩阵记录，以此推算矩阵和，重复该步骤直至低等级列车完成安排。

步骤 4：判断是否满足迭代停止标准。计算拉格朗日问题目标值，再计算，如果 Δ≤ε (ε 为可接受的误差值) 则进行步骤 7，否则进行步骤 6。

步骤 5：判断是否达到最大迭代次数，如果n ＞ N，则进行步骤 7，否则进行步骤 6。

步骤 6：用 Bundle 算法更新拉格朗日乘子，n = n + 1，转步骤 3。

步骤 7：运用可行化方法将初始序列可行化，算法结束。

算法结束后，所有列车的运行时间表 (发车时间 X，到站时间 Y 和停站时间 Z) 确定，可以将其输出到列车时刻表上，或者按照运行时刻铺画在列车运行图上。

3　算例分析

3.1数据整理

以京沪高铁主要技术参数为例[8]，首先将京沪高铁沿线的车站进行编号，上海虹桥站为 01 号，按照上行方向依次编号直到 23 号北京南站。基本数据包括列车运行标尺，即列车区间运行时分、启停车附加时分和图定停站时间；车站基本信息，即车站的上下行股道数，以及车站接车、发车最小间隔时间；价值函数参数；基本图数据等。不同等级的列车其可调整范围不同，等级越低可调整范围越大。目标函数的主要参数如表 1 所示。

表1　价值函数参数及可调整范围

3.2案例设计

基本列车运行图根据京沪高铁现行列车时刻表改编而来，保留原有的车次名称、各中间站的停站时间及列车始发站和始发时间，其他各中间站的发车时间均根据列车运行标尺进行推算。

根据京沪高铁现行列车时刻表，在京沪全线范围内，包括本线列车和跨线列车作为整体调整优化，场景 1 为 9 : 00—9 : 10 的 10 min 内，运行图中包含的列车数是 9 列，场景 2 为 9 : 00—9 : 30 时间段运行图中包含的列车数是 26 列，场景 3 为 9 : 00—10 : 00 时间段内运行图中包含的列车数是 34 列，场景 4 为 9 : 00—11 : 00 的时间段内运行图中包含的列车数是 54 列。

为增加运行调整的难度，场景设计为大面积运行紊乱，通过计算机程序随机生成扰动，每一次列车的始发时间均进行调整，随机生成 10% 的中间站股道故障，使可用股道数减少 1 条，该车站相邻区间运行时分增加 4 min。

3.3计算结果与分析

基于以上各项参数及数据的设定，最大迭代 80 步统计计算结果。当列车数量为 9 列时，曲线“最优值”为每一步迭代的最优值；曲线“下界”为截至当前迭代步为止，所出现的最好值。最优上界为 5 302，最优下界为 5 087，上下界之间的差值为 215，对偶间隙百分比是 4.1%，在实际工程应用上可以认为已经找到最优列车运行调整方案。当开行 26 列车时，下界值为 16 573；当开行列车数为 34 列时，下界值为 28 924；当开行列车数为 54列时，下界值为 42 538，下界值变化趋势如图 3 所示。在图 3 中，在开始 40 步之内曲线缓慢上升，这是由于列车之间的冲突较多，在某些时间点存在竞争，拉格朗日乘子值不断变大，需要通过乘子的不断调整，减少列车之间的冲突点，需要的迭代步数较多。随着乘子的不断调整，原问题目标值不断变大，并且不断趋于稳定，表示已经消除列车之间的冲突点。

图3　下界值变化趋势图

不同场景调整结果比较如表 2 所示，上下界之间差值的相对百分比不超过 10%，在工程应用中认为得到比较精确到解决方案。此外，其计算时间也比较短，最复杂的场景也能在 1 min 时间内求得较优解。综上所述，使用拉格朗日算法可以在较短的时间内对列车运行调整方案进行优化，方便调度员实时调整列车运行图。

表2　调整结果

4　结束语

通过采用基于时空网络方法对高速铁路列车运行调整问题进行建模，将复杂的调度调整问题抽象化，运用基于拉格朗日松弛算法的快速启发式求解算法，通过简化优化条件，并且引入 Bundle 算法获得更精确的拉格朗日乘子，大大提高算法精度。以京沪高速铁路的实际数据为背景进行案例研究，计算结果表明，该模型和算法能够在较短的计算时间(1 min) 内，为数十次列车的运行调整提供接近全局最优解的方案 (对偶间隙不超过10%)，为将来大规模的调度调整问题提供新的解决思路和计算方法。但是，为提高算法速度，在构建模型时对实际问题进行简化和抽象，以车站和区间作为资源，而不是以进路作为资源建模，虽然对于一般高速铁路车站而言，该模型已经完全能够适应列车运行调整的需要，可以疏解资源占用冲突情况，但对枢纽站具有一定局限性，可以在将来的研究过程中细化模型约束条件，使其更加符合实际情况。

[1] 王宏刚，张 琦，王建英，等. 基于遗传算法的高速铁路行车调整模型[J]. 中国铁道科学，2006，27(3)：96-100. WANG Hong-gang，ZHANG Qi，WANG Jian-ying，et al. GA-based Model of Train Operation Adjustment for High-Speed Railway[J]. China Railway Science，2006，27(3)：96-100.

[2] 许 红，马建军，龙建成. 客运专线列车运行图编制模型及计算方法的研究[J]. 铁道学报，2007，29(2)：1-7. XU Hong，MA Jian-jun，LONG Jian-cheng. Research on the Model and Algorithm of the Train Working Diagram of Dedicated Passenger Line[J]. Journal of the China Railway Society，2007，29 (2)：1-7.

[3] 谢美全，聂 磊. 周期性列车运行图编制模型研究[J]. 铁道学报，2009，31(4)：7-13. XIE Mei-quan，NIE Lei. Model of Cyclic Train Timetable[J]. Journal of the China Railway Society，2009，31(4)：7-13.

[4] 汪 波，杨 浩，牛 丰，等. 周期运行图编制模型与算法研究[J]. 铁道学报，2007，29(5)：1-6. WANG Bo，YANG Hao，NIU Feng，et al. Study on Model and Algorithm of Periodic Train Diagram Generation[J]. Journal of the China Railway Society，2007，29(5)：1-6.

[5] XIE M，LI X. Railway Timetable Rescheduling based on the Feedback of Train-set Circulation[J]. Procedia-Social and Behavioral Sciences，2012，43(43)：781-789.

[6] Vansteenwegen P，Oudheusden D V. Decreasing the Passenger Waiting Time for an Intercity Rail Network[J]. Transportation Research：Part B，2007，41(4)：478-492.

[7] 康 宁，武小悦. 基于拉格朗日松弛的航天测控调度上界求解算法[J]. 国防科技大学学报，2011，33(3)：38-43. KANG Ning，WU Xiao-yue. TT&C Scheduling Upper Bound Solution Algorithm based on Lagrangian Relaxation[J]. Journal of National University of Defense Technology，2011，33(3)：38-43.

[8] Wikipedia. Beijing-Shanghai High-Speed Railway[EB/OL]. (2015-10-08) [2016-02-19]. https://en.wikipedia.org/wiki/ Beijing%E2%80%93Shanghai_High-Speed_Railway.

责任编辑：吴文娟

成都铁路局增加运力满足市民踏青游需求

随着天气转暖，外出踏青游玩的旅客日益增多，成都铁路局扩增短途运能，灵活调整动车组上线运用模式，保证日均可以增加 1.8 万张票额，满足市场需求。

2016年2月29日—3月3日期间，成都铁路局将以成渝达三角区和四川省内高铁路网为重点，进一步扩增短途运能，灵活调整动车组上线和入库检修数量，最大限度满足旅客出游需求。

成都铁路局将增开成都东至江油 C6214 次、江油至峨眉山 C6317 次、峨眉山至成都东 C6270次、成都东至峨眉山 C6269 次、峨眉山至成都东 C6272 次、成都东至峨眉山 C6271 次等7趟绵成乐城际动车组；重联加开重庆北至内江北G8622 次、内江北至成都东 G8624 次、成都东至永川东 G8621 次、永川东至成都东 G8626 次、成都东至内江北 G8623 次等 6 趟成渝高铁动车组，并将重庆北至成都东 G8508 次、G8513 次等 7 趟动车实行重联运行，保证日均可以增加 1.8 万张票额。

（摘自《人民铁道》报）

Study on Optimization Model of High-speed Railway Train Operation Adjustment

Based on expounding study status of train operation adjustment, targeting with problems existing in daily train operation adjustment, according to characteristics of resources occupation of high-speed railway train operation, each train is given a value, and taking maximum overall value as the optimization object, the mathematical model of resources occupation based on time-space network is established, the model is simplified and solved by using improved Lagrangian relaxation algorithm, and then, taking Beijing-Shanghai high-speed railway as an example, the result shows the algorithm could satisfy the demand of actual application.

Operation Plan; Cost Function; Lagrangian Relaxation; Optimization

1003-1421(2016)03-0034-07+1；U284.59

A

U292.4

10.16668/j.cnki.issn.1003-1421.2016.03.07

2016-02-19

中国铁道科学研究院基金项目(2015YJ054)