驾驶员制动和转向避撞极限

李 霖， 朱西产， 陈海林

(1.同济大学 智能型新能源汽车协同创新中心, 上海 201804；2. 上海国际汽车城(集团)有限公司，上海 201804)



驾驶员制动和转向避撞极限

李 霖1,2， 朱西产1， 陈海林2

(1.同济大学 智能型新能源汽车协同创新中心, 上海 201804；2. 上海国际汽车城(集团)有限公司，上海 201804)

结合驾驶员避撞行为特征和车辆动力学特性，对驾驶员的制动和转向避撞极限进行了研究，得到了制动避撞和转向避撞的临界TTC(time-to-collision)值，并对比分析了两种避撞方式的适用性以及道路摩擦系数、重叠率等因素的影响.结果表明，转向避撞在高相对速度、低附着系数、低重叠率等工况下相比于制动避撞更有优势.

制动； 转向； 避撞极限

先进驾驶辅助系统(Advanced Driver Assistance Systems, ADAS)是智能汽车安全技术的重要组成部分，在紧急工况下，当前最有代表性的ADAS系统是自动紧急制动系统(Autonomous Emergency Braking, AEB).AEB系统在碰撞危险非常高时通过紧急制动来避免碰撞或减轻碰撞程度，这类系统已经较为成熟，但当前的AEB系统只能在驾驶员无避撞行为或只有制动行为时才能够有效帮助驾驶员避免事故或减轻事故的伤害，如果在介入时驾驶员有非预期行为(比如转向、加速等)，无论驾驶员的操作是否正确，AEB系统都会自动取消介入，将控制权完全交还给驾驶员.

但驾驶员行为分析结果表明，在紧急工况下，相当部分驾驶员存在转向避撞行为[1]，同时由于转向避撞在高相对速度、低附着系数、低重叠率等工况下相对于制动避撞所需的纵向距离更小，避撞效能更高[2-4]，因此有必要对驾驶员的紧急转向行为进行辅助.目前国际上已经开始了对紧急转向避撞技术的研究[1,5].

在开发AEB及紧急转向避撞系统时，需要对制动和转向所需的最短纵向距离，也就是临界避撞距离，进行准确的定量分析，以确定在特定的工况下某种避撞方式是否可行，以及某种避撞方式是否相对于另一种避撞方式更有优势.这些分析结果是危险估计的基础.目前已经有不少研究人员进行了这方面研究，但分析的基础要么基于单自由度质点模型，忽略了车辆动力学特性的影响，得出的值只适用于定性分析[3]；要么只是从车辆的动力学出发，分析车辆的避撞极限[2,4]，但由于智能汽车安全系统的作用是对驾驶员提供辅助，因此最短纵向距离分析应当结合驾驶员的行为特性，探索驾驶员的极限状态.因此，本文将结合驾驶员避撞行为特征对制动和转向避撞的临界避撞距离进行定量分析，作为开发集成紧急制动和转向避撞控制的基础.

1 制动避撞临界距离

实际危险工况下驾驶员的极限紧急制动避撞行为产生的车辆减速度响应可用图1表示.设车辆初始减速度为a0，驾驶员开始制动后，由于制动器的延迟，在时间td后车辆的制动减速度才开始发生变化，然后以梯度jmax达到最大制动减速度amax并保持amax不变直到车辆停止或成功避免碰撞.

根据文献[6]中对危险工况下驾驶员制动行为的分析结果[6]，虽然大部分驾驶员不能充分利用车辆的制动潜能，但驾驶员最大制动减速度绝对值的90百分位值在0.8g左右，说明仍然有部分驾驶员达到了车辆的最大制动减速度.为了避免误作用，这里设定驾驶员制动能够达到的最大制动加速度与车辆能够达到的最大制动减速度一致.而95%的驾驶员制动梯度小于20.82 m·s-3，因此设定加速度梯度jmax=21 m·s-3.

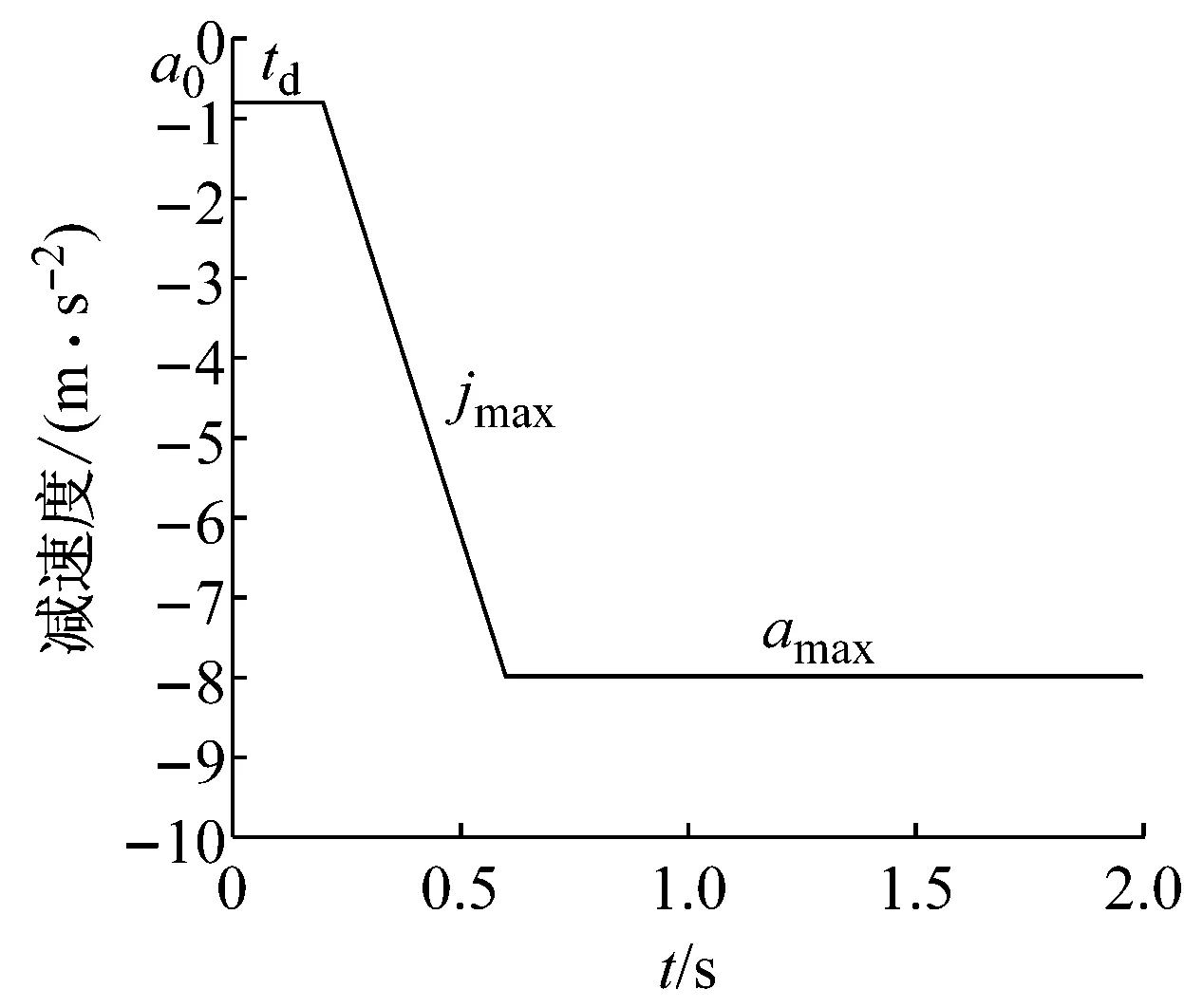
图1 驾驶员制动输入示意图

制动器延迟时间td随车辆不同而不同，但装配AEB系统的车辆基本都带有制动辅助(braking assist, BA)功能，在紧急情况下制动辅助系统可通过预蓄压将td减小到0，因此这里设定td=0.不失一般性，以两车追尾工况为例，目标车(前车)静止，本车(后车)初始速度为v0，初始制动减速度a0=0，本车通过紧急制动避撞操作停止后与目标车距离SM=0.1 m，设道路摩擦系数μ=0.8，本车能够达到的最大制动减速度绝对值amax=μg.

当车速很低时(小于5.3 km·h-1)，车辆还未达到最大制动减速度时车辆就已经停止，这种情况下本车危险性较低，因此不做考虑，则

(1)

(2)

(3)

(4)

式(1)～(4)中：t1为达到最大制动减速度所需要的时间；t2为从达到最大制动减速度到车辆停止的时间；S为车辆制动距离；tc为临界TTC(time-to-collision)值.图2为不同车辆初速度下的tc值，可见考虑和不考虑减速度梯度时tc的差异随着车速升高而增大，当本车车速为100 km·h-1时，两者之间的差异达到0.20 s(图2)，在紧急工况下，0.20 s的差异会导致完全不同的避撞效果.

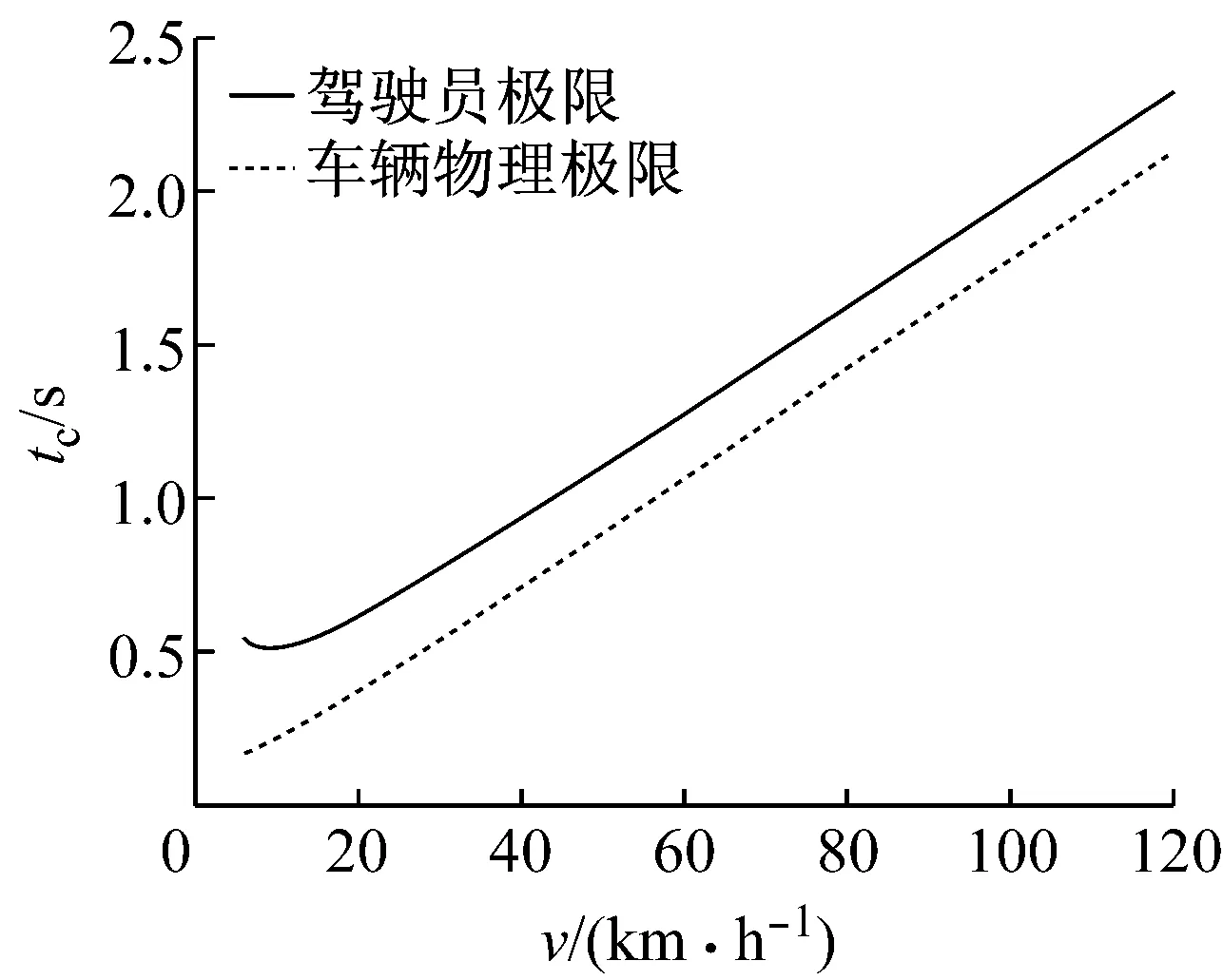
图2 制动避撞的临界TTC值

2 转向避撞临界距离

Biral等[7]、Bertolazzi等[8]的研究结果表明，驾驶员在规划转向路径时大致可用最优控制进行描述，即遵循“最大方向盘转速最小(minimum jerk)”的原则，让驾驶过程尽量平滑.因此，本文采用最优控制方法模拟驾驶员的转向避撞行为，分析驾驶员转向避撞所需的最短纵向距离.

不失一般性，考虑图3所示的前车静止工况.将两车都视作相同大小矩形，长5.2 m，宽2.0 m，两车重叠率为100%.车辆质心到车辆最前端的距离为2.5 m，到车辆最后端距离为2.7 m.

图3 转向避撞示意图

2.1 车辆模型

为了获得更为准确的结果，这里采用二自由度单轨车辆模型，状态变量为质心侧偏角β和横摆角速度γ.由于转向避撞过程时间很短，且为了保持车辆避撞后的机动性需尽量减少速度损失，因此这里设车速恒定为u0，即不考虑制动的影响.车辆的状态方程为

(5)

式中：m为车辆质量；Iz为车辆绕z轴的转动惯量；lf为车辆质心到前轴的距离；lr为车辆质心到车辆后轴的距离；Fxf,Fyf分别为单个前轮的轮胎力在车辆坐标系下的分量，由于不考虑车轮的左右载荷转移，因此左右两个车轮的轮胎力相等；同理，Fxr,Fyr分别为单个后轮的轮胎力在车辆坐标系下的分量.

采用Pacejka轮胎模型，并将车辆坐标系变量转换到大地坐标系，得到非线性单轨车辆模型为

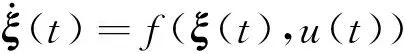
(6)

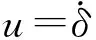
2.2 安全约束

如图4所示，车辆质心在大地坐标系中坐标为(X,Y)，航向角为ψ，车辆质心到车辆最前端距离为Lf，到车辆最后端距离为Lr，车辆宽度为W，则车辆4个角点的坐标为

(7)

式中：下标lf,rf,lr,rr分别代表左前、右前、左后、右后4个角点.

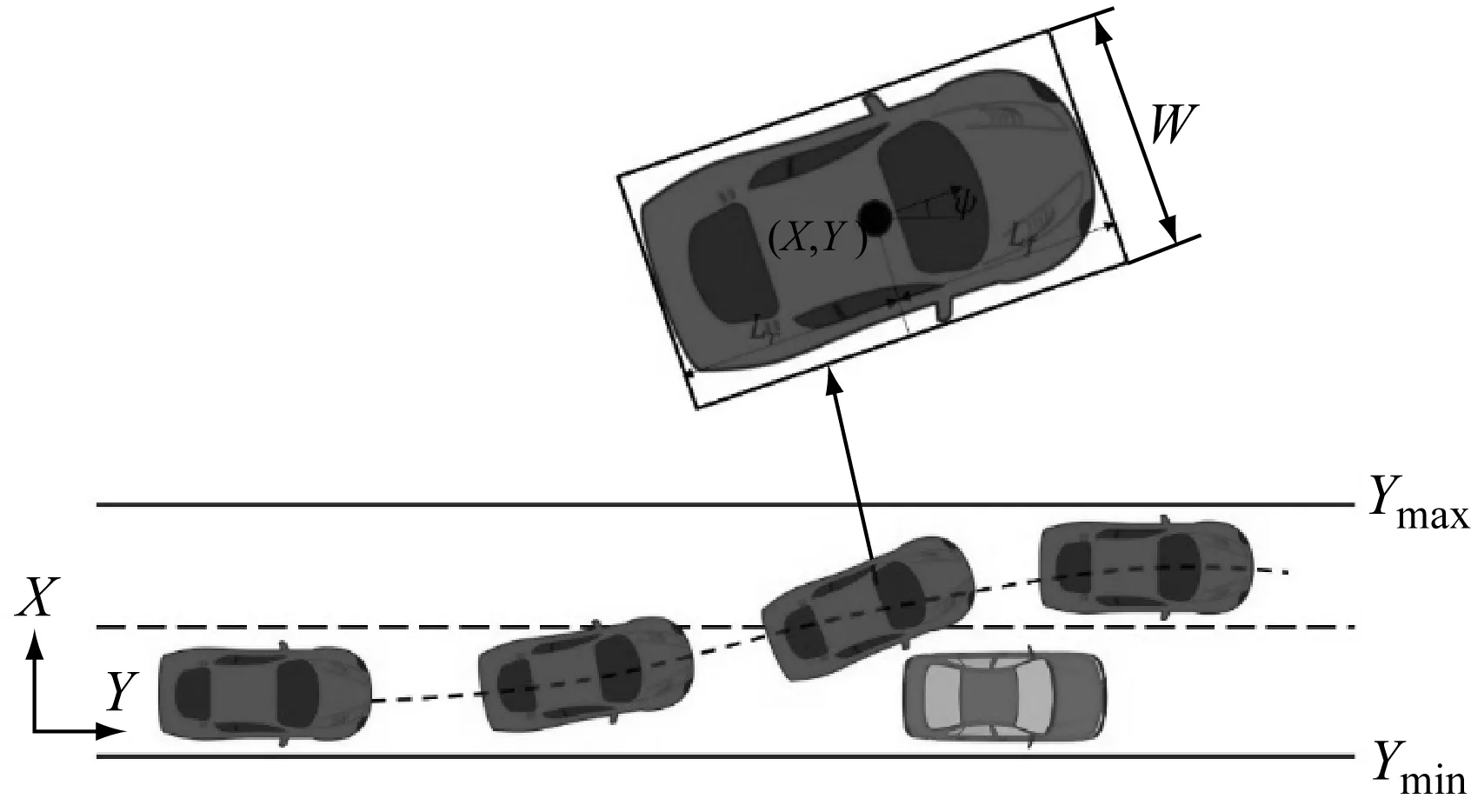
图4 安全约束示意图

在转向避撞时，车辆必须保持在规定的道路上，则必须满足

(8)

式中：Ymax，Ymin分别为道路的上下边界，由道路边缘、路肩、护栏等决定.

驾驶员在转向避撞时车辆的侧向加速度不能超过一定的限值，否则不仅会使驾驶员产生不适，而且可能导致车辆失稳.因此侧向加速度必须满足|ay|≤ay,max，即

(9)

ay,max由道路摩擦系数、车辆的抗侧翻能力、驾驶员生理限制等决定，通常情况下ay,max≤μg.

如图5所示，以向左转向避撞为例，在本车通过目标车时，目标车左后角点(XO,YO)到本车右侧边界的距离D必须大于一定的安全距离DSM，即

(10)

式中：k为本车右侧边界所在直线的斜率，k=tanψ.

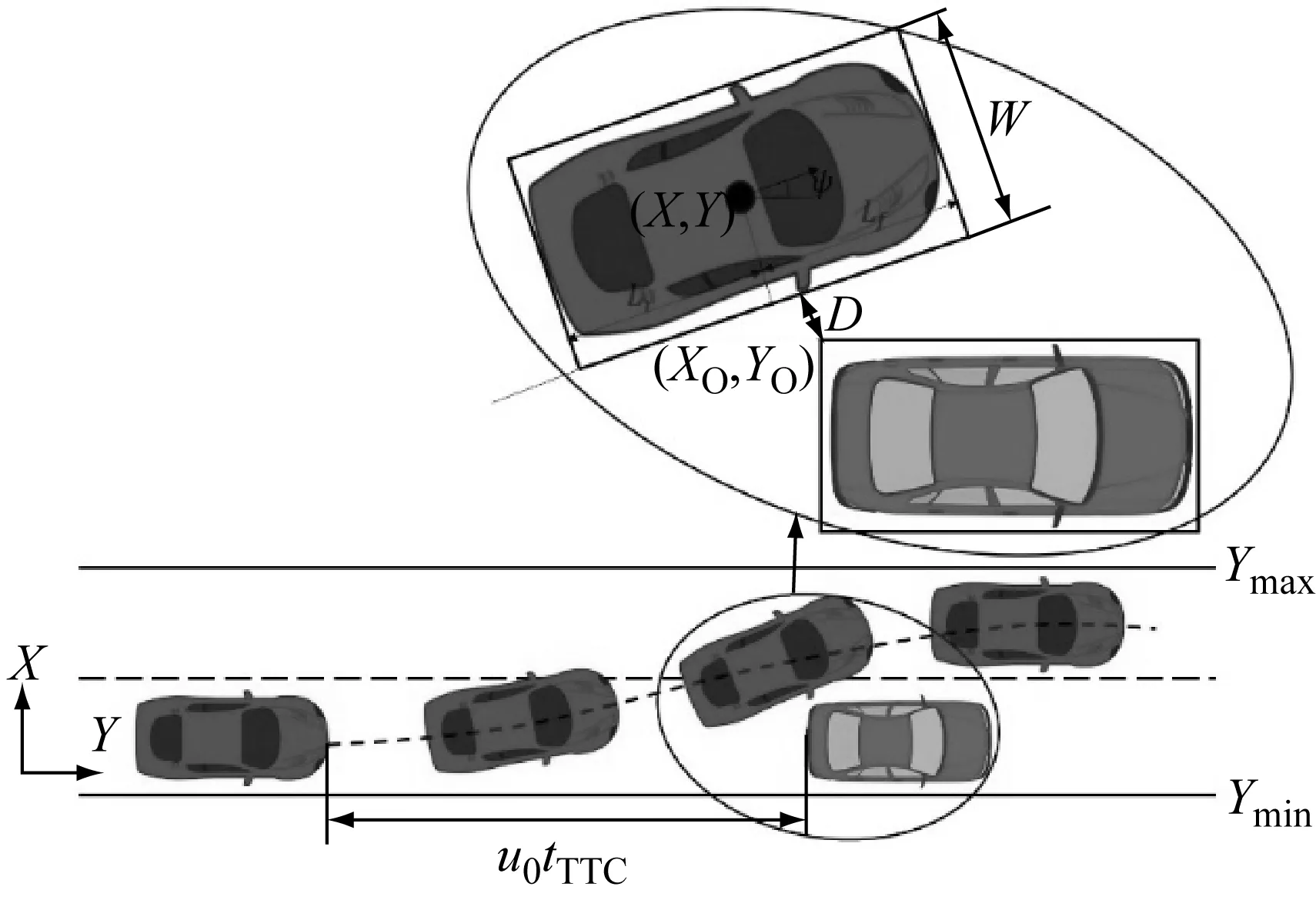
图5 避撞约束示意图

2.3 执行器约束

在通过紧急转向进行避撞时，由于车辆的结构以及驾驶员的生理能力限制，转向角和转向角速度都不能超过一定的限值，即

(11)

将安全约束和执行器约束综合在一起，可以用下式表示:

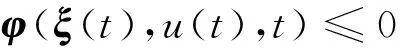
(12)

式中：ξ(t)为车辆状态变量;u(t)为车辆输入.

为了保证最优化计算的稳定性，此处对约束条件进行松弛，得到

(13)

式中：ε为松弛变量，是很小的非负常数.

2.4 最优控制问题求解

本文将转向避撞过程分为两个阶段，第一个阶段起始时刻t01=0，终止时刻tf1=tTTC(TTC值)，第二个阶段起始时刻t02=tTTC，终止时刻tf2不加限制.

第一节阶段的目标函数为

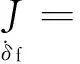
(14)

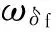
第一阶段的边界条件为

(15)

在tf1时刻，除满足安全约束、执行器约束外，目标车辆左后角点到本车右侧边界的距离D(tf1)要满足以下事件约束

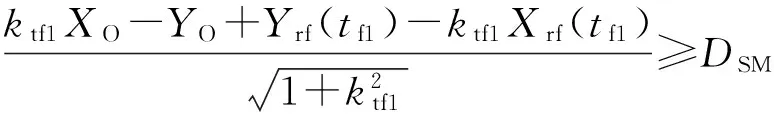
(16)

式中：ktf1=tanψ(tf1).

第二阶段的目标函数为

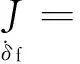
(17)

式中：ωf为第二阶段终值目标函数加权系数，该值越大表示要求tf2越小.

第二个阶段的初值边界条件与第一阶段的终值边界条件相同，第二阶段的终值边界条件为

(18)

式中：Yref为期望侧向位移.

将上述过程转换为以下最优控制问题：

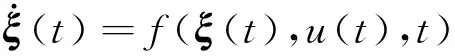
φ(ξ(t),u(t),t,ε)≤0，

ε≥0，l(ξ(t0),t0,ξ(tf),tf)=0，

t∈[t0,tf]

(19)

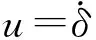
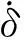
采用上述最优控制算法，计算不同车速下的转向避撞所需tc值，最终结果如图7所示.可以看出，在一定类型工况下，tc值随着车速升高而降低，这是因为最大侧向加速度以及侧向加速度梯度都随着车速升高而增大，使得通过转向避撞更容易，因此tc值减小到一定速度后，最大侧向加速度以及侧向加速度梯度都饱和，因此tc值不再变化.

3 制动和转向临界避撞距离对比

将制动避撞以及转向避撞所需的tc值绘制在一起，如图8所示.在相对车速较低(小于43.05 km·h-1)时，制动避撞的tc值比转向避撞所需的tc值低，因此自动紧急制动系统在相对车速较低时是一个最优的选择，因为此时通过转向无法避免碰撞.

当相对车速较高时(大于43.05 km·h-1)，转向避撞所需的tc值更低，说明此时虽然制动无法避免碰撞，但通过转向还能够避免碰撞，因此紧急转向避撞控制在相对车速较高时相比于紧急制动控制可以提供更好的避撞效果.

在道路摩擦系数不同，重叠率不同时，制动避撞与转向避撞所需的tc值对比如图9所示.可见当道路摩擦系数从0.8降低到0.3时，临界相对速度从43.05 km·h-1降低到24.73 km·h-1，说明在湿滑路面上，转向避撞相对于制动避撞的优势更大.保持道路摩擦系数为0.8不变，本车与目标车重叠率从100%降低到50%时，临界相对速度从43.05 km·h-1降低到34.84 km·h-1，说明在小重叠率时，转向避撞的有效性更高.

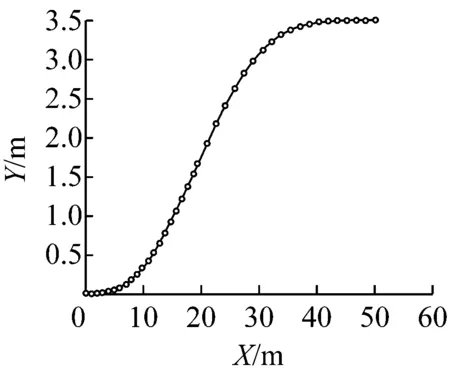
a 车辆轨迹

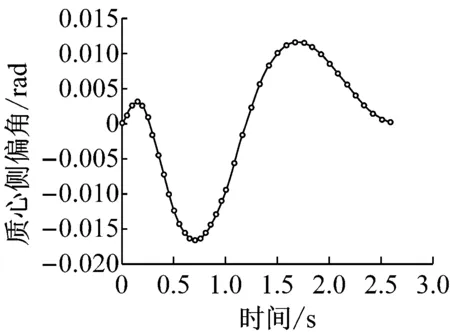
b 质心侧偏角

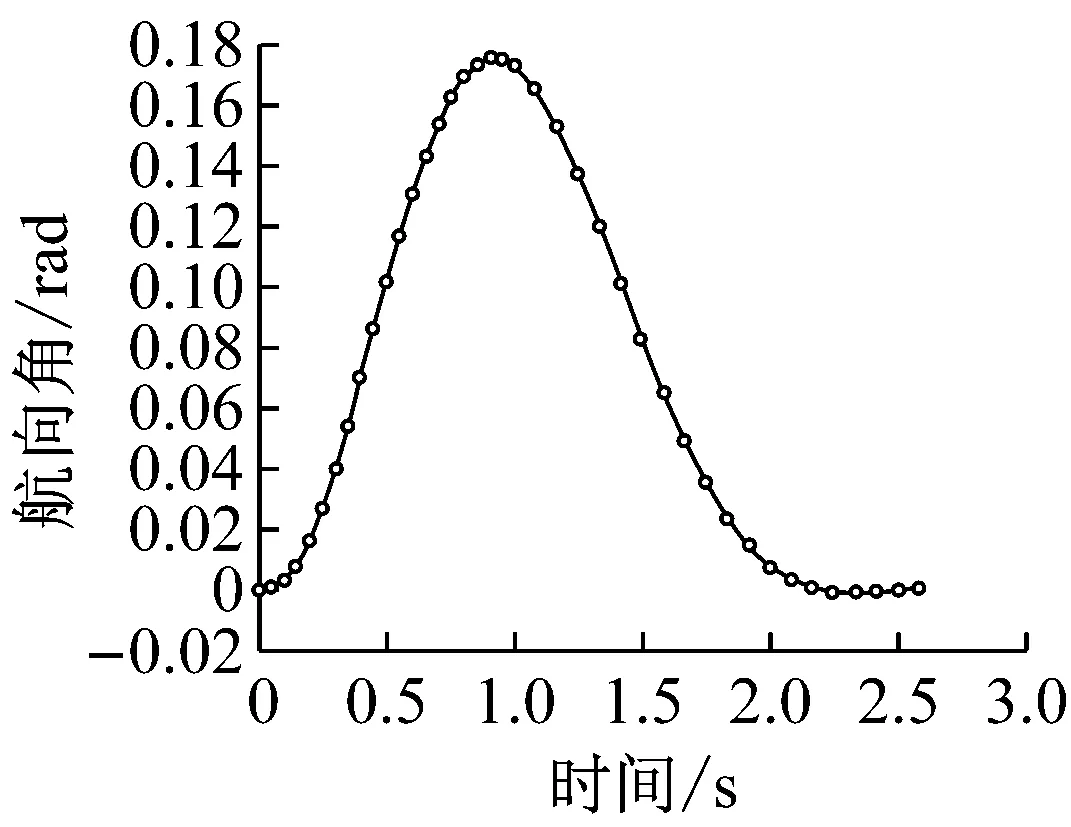
c 航向角

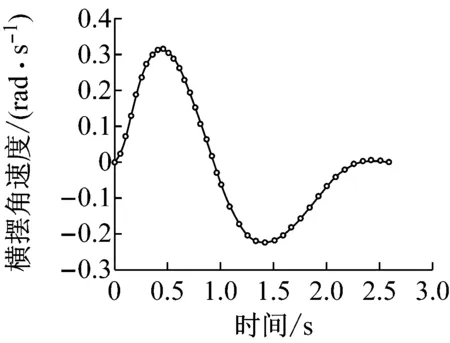
d 横摆角速度

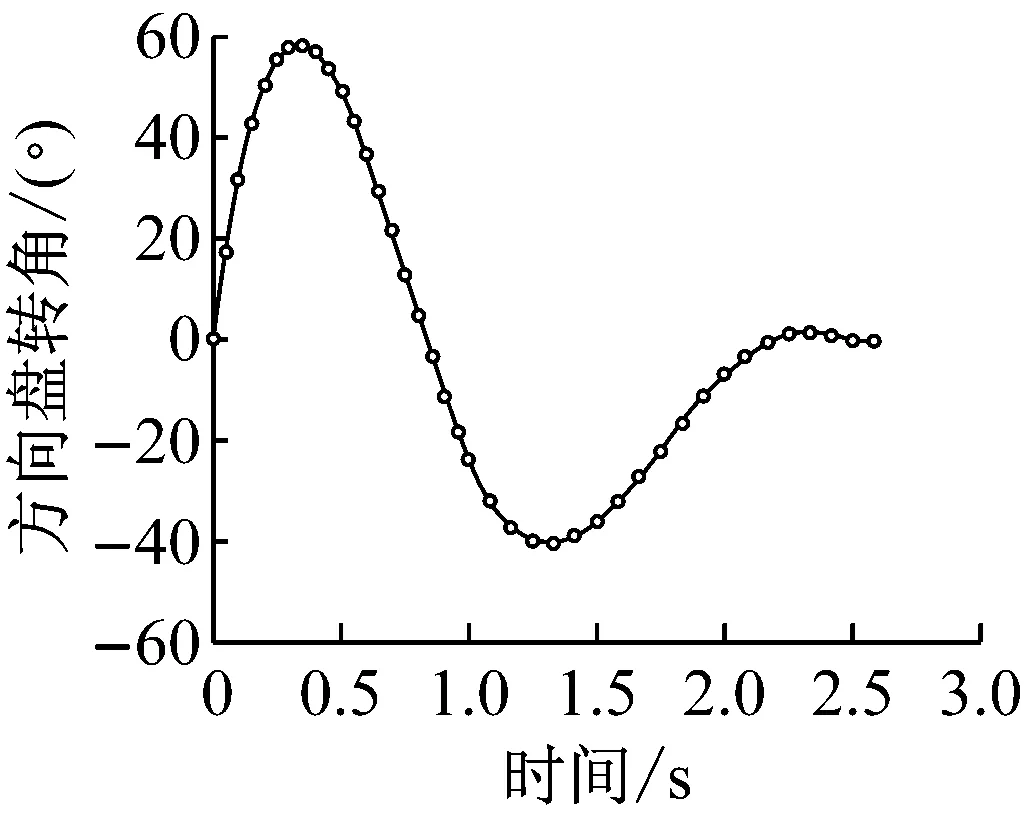
e 方向盘转角输入

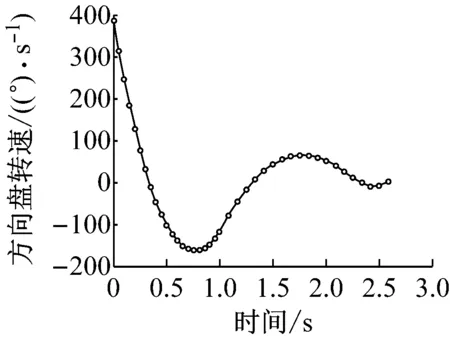
f 方向盘转速输入

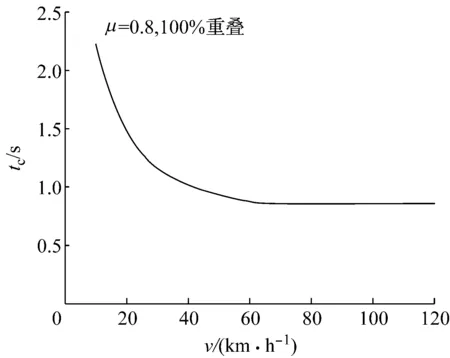
图7 不同车速下转向避撞所需的tc值

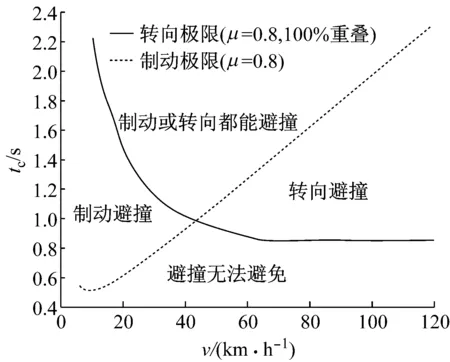
图8 tc值对比

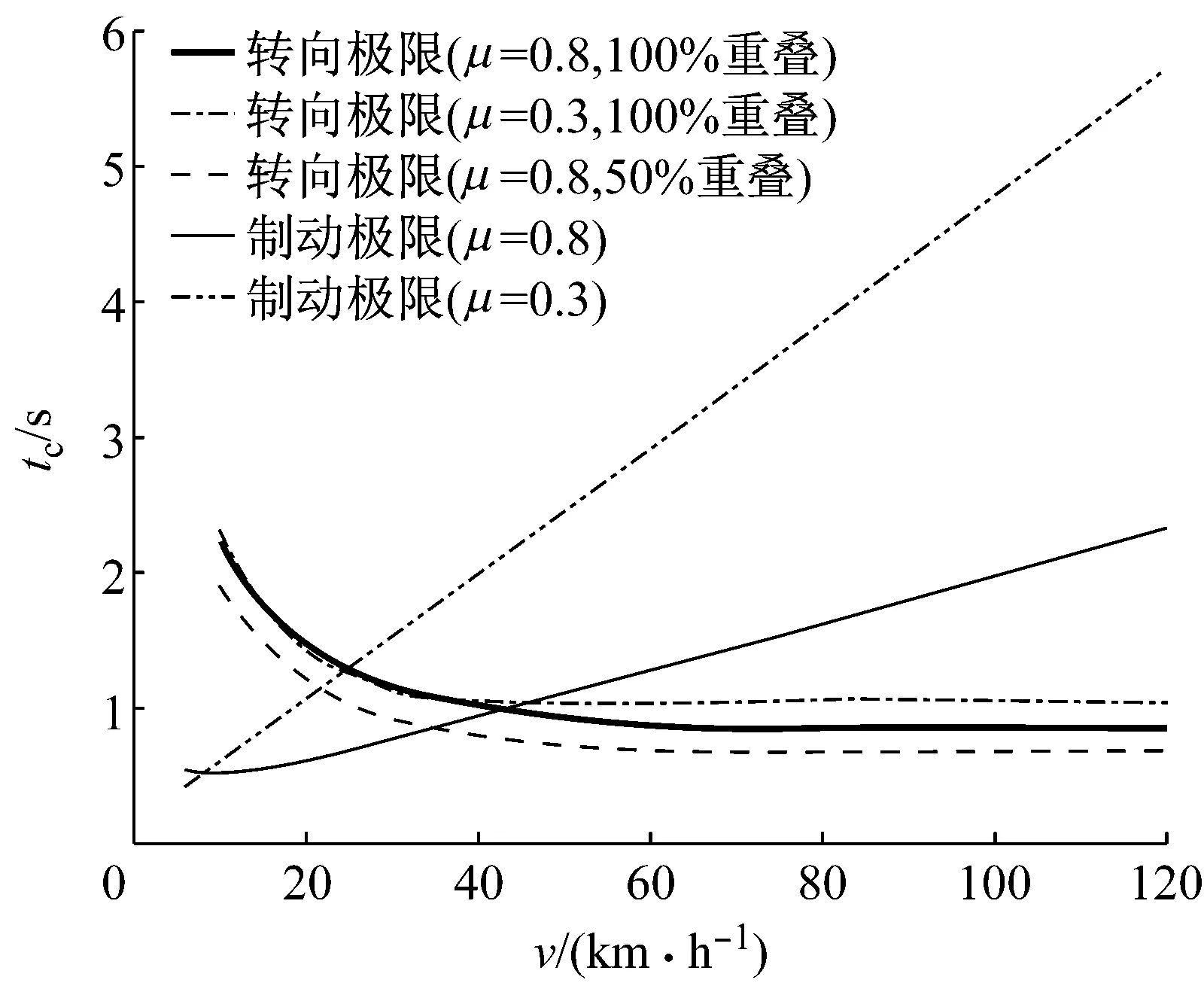
图9 不同工况下制动避撞和转向避撞所需的tc值

4 结论

本文结合驾驶员避撞行为特征和车辆动力学特性，对驾驶员的制动和转向避撞极限进行了定量分析和对比.首先通过驾驶员的紧急制动避撞特性对制动避撞所需的tc值进行了分析，然后结合车辆动力学模型和驾驶员紧急转向避撞行为特征参数，构建最优控制问题并采用高斯伪谱法求解，得到了驾驶员转向避撞的tc值，最后对比了制动和转向两种避撞方式的适用性以及车速、道路摩擦系数、重叠率等的影响.本文的研究结果可以为开发制动和转向避撞控制策略提供参考，同时计算驾驶员转向避撞极限的方法也可用于转向避撞控制的路径规划算法开发.

[1] Eckert A, Hartmann B, Sevenich M,etal. Emergency steer & brake assist: a systematic approach for system integration of two complementary driver assistance systems[C/CD]//Proceedings of the 22nd International Technical Conference on the Enhanced Safety of Vehicles (ESV). Washington D C: NHTSA, 2011.

[2] Bevan G P, Gollee H, O’Reilly J. Trajectory generation for road vehicle obstacle avoidance using convex optimization[J]. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 2010, 224(4):455.

[3] Hattori Y, Ono E, Hosoe S. Optimum vehicle trajectory control for obstacle avoidance problem [J]. IEEE/ASME: Transactions on Mechatronics, 2006, 11(5):507.

[4] Mårtensson J, Nybacka M, Jerrelind J,etal. Evaluation of safety distance in vehicle platoons by combined braking and steering[C/CD]//11th International Symposium on Advanced Vehicle Control. Seoul: Japan Society of Mechanical Engineers (JSAE), 2012.

[5] Fausten M. Accident avoidance by evasive manoevres[C/CD]//Proceedings of the 4th Tagung Sicherheit durch Fahrerassistenz (TVSD). Munich: TVSD, 2010.

[6] Li L, Zhu X, Ma Z. Driver braking behaviour under near-crash scenarios [J]. International Journal of Vehicle Safety, 2014, 7(3): 374.

[7] Biral F, Da Lio M, Bertolazzi E. Combining safety margins and user preferences into a driving criterion for optimal control-based computation of reference maneuvers for an ADAS of the next generation[C]// Proceedings of 2005 IEEE Intelligent Vehicles Symposium. Las Vegas : IEEE, 2005: 36-41.

[8] Bertolazzi E, Biral F, Da Lio M,etal. Supporting drivers in keeping safe speed and safe distance: the SASPENCE subproject within the European framework programme 6 integrating project PReVENT[J].IEEE Transactions on Intelligent Transportation Systems, 2010, 11(3):525.

[9] 刘英杰, 赵又群, 许健雄, 等. 基于 Gauss 伪谱法的紧急避让汽车操纵逆动力学[J]. 机械工程学报, 2012, 48(22): 127.

LIU Yingjie, ZHAO Youqun, Xu Jianxiong,etal. Vehicle handling inverse dynamics based on gauss pseudospectral method while encountering emergency collision avoidance[J]. Chinese Journal of Mechanical Engineering, 2012, 48(22): 127.

[10] Patterson M A, Rao A V. GPOPS-II: A MATLAB software for solving multiple-phase optimal control problems using hp-adaptive gaussian quadrature collocation methods and sparse nonlinear programming[J]. ACM Transactions on Mathematical Software (TOMS), 2014, 41(1):1.

Drivers’ Collision Avoidance Limit by Braking and Steering

LI Lin1,2, ZHU Xichan1, CHEN Hailin2

(1.Collaborative Innovation Center of Intelligent New Energy Vehicle, Tongji University, Shanghai 201804，China; 2. Shanghai International Automobile City Group Co.,Ltd., Shanghai 201804, China)

The limit of drivers’ capacity of collision avoidance by braking and steering were analyzed in this paper based on the charateristics of drivers’ collision avoidance manervers and vehicle dynamics. The critical values of time-to-collision(TTC) of these two different collision avoidance manervers were obtained and compared. The influences of road coefficient and overlap rate were also analyzed. The results quantitatively show that under certain conditions such as high relative speed, low friction coefficient, and small lateral overlap, the collision avoidance by steering is easier than by braking.

braking; steering; collision avoidance limit

2015-12-09

李 霖(1986—)，男，工学博士，主要研究方向为智能网联汽车技术.E-mail:pengxililin@gmail.com

朱西产(1962—)，男，教授，博士生导师，工学博士，主要研究方向为汽车主动、被动安全技术.E-mail:xczhu@163.com

U461.9

A