重载铁路轨道路基系统动位移空间分布特征

杨新文， 龙天航， 周顺华

(同济大学 道路与交通工程教育部重点实验室，上海 201804)



杨新文， 龙天航， 周顺华

(同济大学 道路与交通工程教育部重点实验室，上海 201804)

建立了重载货车-有砟轨道-路基系统耦合动力学模型.分析计算了在轨道随机不平顺激励下30 t轴重重载铁路轨道-路基系统动位移的分布规律.计算结果表明：①轨道-路基系统各结构层动位移状态较为复杂，在重载货车通过的过程中，所受荷载也处于循环往复的加载和卸载状态.②在有砟轨道-路基系统的动位移的3个位移分量中，竖向动位移的幅值较大，横向动位移以及纵向动位移的幅值均不超过竖向动位移幅值的6%；而沿横向，动位移的分布较为缓和，其最大波动幅值不超过0.2 mm，可近似看做均匀分布.③轨道-路基系统动位移沿竖向的变化，大体分为3个阶段：在钢轨到轨枕之间，出现明显突变；在轨枕层区域的衰减幅度较小；在道床层至基床表层及下部结构，竖向动位移表现为沿深度方向不断衰减，并且衰减速率随着深度的增加也在不断减小.

重载铁路； 轨道结构； 路基； 动位移； 空间分布

重载铁路在服役过程中会经历重载货车荷载的反复加/卸载，这对于重载铁路轨道结构的疲劳抗性以及下部基础的沉降都会产生很大的影响.Knothe[1]和Grassie[2]早在1995年就指出，充分考虑轨道、路基和结构物的有效动态分析模型是今后的主要研究方向之一.Powrie等[3-5]对有砟轨道的动力响应进行了参数分析，并将现场实测得到的数据对模型进行了验证.梁波等[6]用一种带频变特征的激振力模拟列车动荷载，对路基在不平顺条件下的动态响应进行了分析，并在随后的研究中对已有的列车荷载表达式进行了修正与完善[7].高建敏等[8-9]根据车辆-轨道耦合动力学理论建立了重载车辆-有砟轨道系统耦合动力学模型，分析了轨道结构参数以及运营条件对有砟轨道下沉破坏的影响规律.近年来高亮等[10-11]建立考虑多车效应的重载列车-轨道系统精细化动力分析模型，对重载铁路曲线地段列车-轨道系统动力性能及曲线参数影响规律进行了深入研究.薛继连等[12-14]针对朔黄铁路开行30 t轴重时既有轨道的适应性与强化措施等问题，采用动力仿真分析与实车试验相结合的方法，分析了30 t轴重下轨道结构的动力学适应性，进一步分析了朔黄铁路中的隧道、桥梁对开行30 t轴重列车的适应性.

翟婉明等[15-20]针对重载铁路低动力设计、重载货车轴重与速度匹配关系、开行大轴重列车的适用条件以及列车对轨道和路基的动力影响等方面开展了一系列研究，其研究为我国重载铁路的建设与维护提供了有益的参考.

近年来对轨道动力学的研究方法主要有两类，一是利用有限元方法建立精细化轨道模型，将列车荷载看作一列受激振影响的移动荷载;二是利用车-轨耦合动力学理论建立车辆-轨道耦合模型，考虑车辆各结构的耦合振动，对轨道和路基的处理则采用多层支撑梁模型.前者对车辆系统的考虑不够全面，后者无法分析轨道-路基系统动力响应的空间分布.

本文基于车辆-轨道耦合动力学理论，采用有限元方法建立了车辆-有砟轨道-路基耦合动力学模型，车辆系统被视为多刚体系统，有砟轨道-路基系统采用梁-实体单元来模拟，通过轮轨关系将车辆与轨道-路基系统联系在一起.在计算分析时，采用新型快速显式积分法与Newmark积分法相结合的方法进行仿真，其中车辆系统采用较为快速的新型快速显示积分法进行动力学求解，而有砟轨道-路基耦合系统动力解采用相对精确的Newmark积分法求得.利用建立的模型计算分析了30 t轴重重载货车通过时重载铁路轨道-路基系统的动位移的空间分布规律，并与相关文献结果进行了对比，验证了模型的正确性.

1 重载货车轨道路基耦合模型

1.1 耦合模型

根据重载铁路特点建立了重载货车-有砟轨道-路基耦合动力学模型，耦合系统从上至下依次为车辆子系统、有砟轨道子系统和路基子系统.

车辆子系统中，车辆被视为一个以一定速度运行在轨道上的多刚体系统，重载货车模型采用二系悬挂形式建模，如图1所示.模型考虑了车体的沉浮和点头自由度，前后转向架的沉浮和点头自由度，以及4个轮对的沉浮自由度，一共10个自由度.车体与两个转向架之间用二系弹簧悬挂联结，每台转向架与两个轮对之间为一系弹簧悬挂联结.本文在动力加载时，各节车辆的轴重均视为相同，由于关注的是垂向力对轨道与路基动力学性能的影响，故本文车辆系统只考虑一节车.

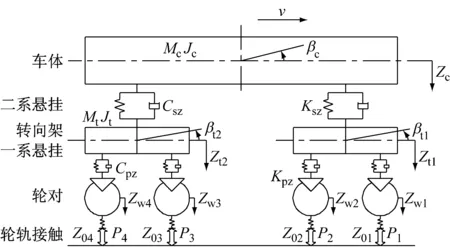
图1 重载货车子系统模型

有砟轨道系统主要由钢轨、扣件、轨枕和道床所组成.模型中，钢轨视为连续弹性离散点支承基础上的有限长Euler梁，具有垂向自由度；轨枕和道床采用实体单元进行精细化建模；钢轨与轨枕之间用线性弹簧阻尼单元联结.

路基子系统由路基表层和路基底层构成，路基表层是主要的受力部位，而列车荷载传递到路基底层时衰减至很小，故本文着重以路基表层的动力响应来揭示其与轨道结构的相互影响，建模时用实体单元模拟，路基底层以及下部结构用线性弹簧和黏性阻尼单元来模拟，如图2所示.

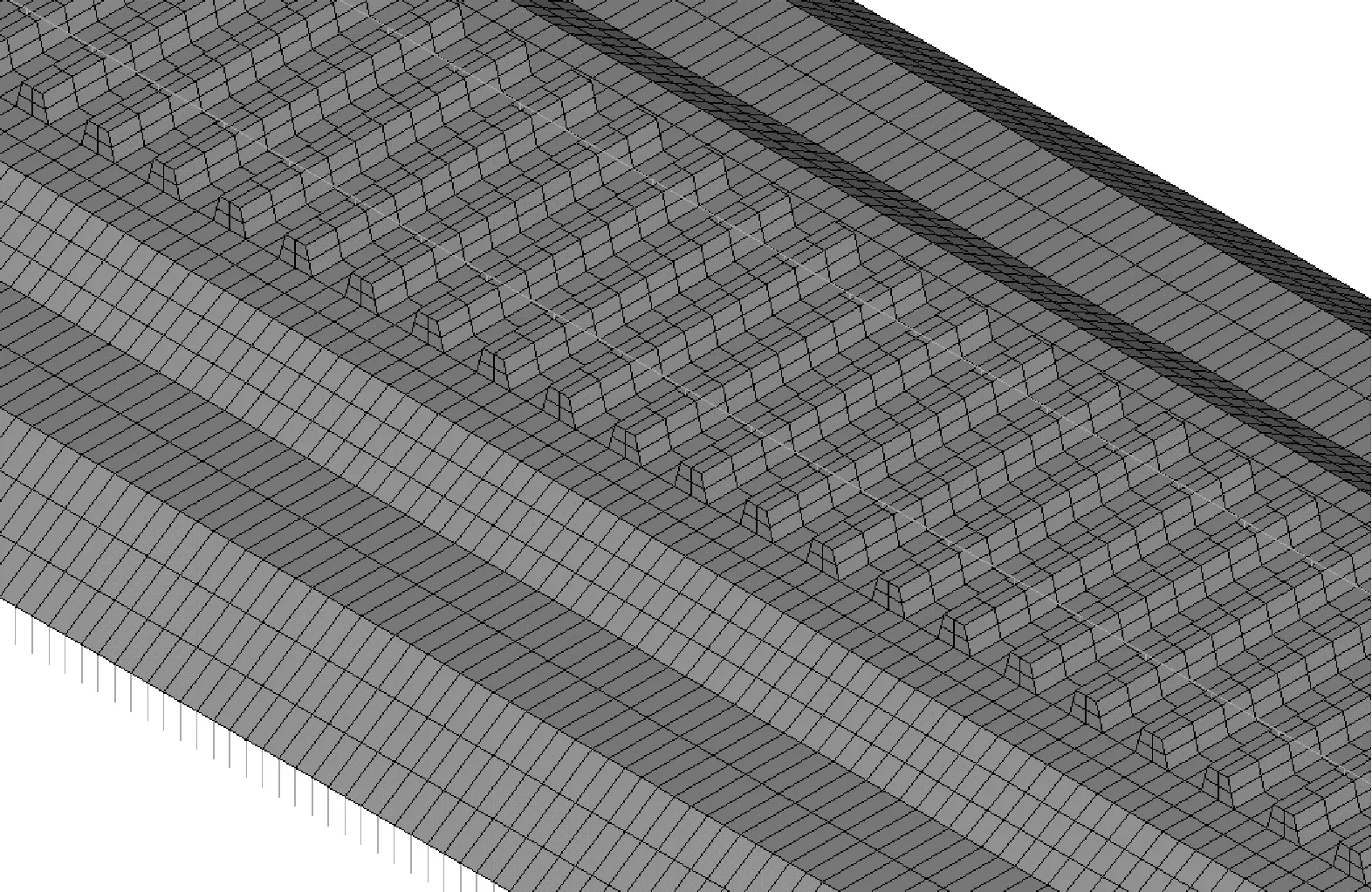
图2 轨道路基系统有限元模型

轨道和路基系统模型沿纵向长50 m，总单元数为23 655，模型选取为半结构，对纵断面施加对称约束，对模型底部施加全约束.

1.2 耦合系统动力学方程

重载货车系统可根据达朗贝尔原理得到其运动微分方程为

(1)

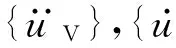
利用有限元方法建立有砟轨道-路基耦合系统运动微分方程为

(2)

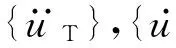
车辆与轨道两个子系统之间通过轮轨滚动接触理论来联系，轮轨接触力成为联系两个子系统的纽带.车辆系统和轨道系统通过轮轨力来相互耦合，fV和fT均含有轮轨垂向力Pwk，其计算公式如下：

(3)

式中：Zw，Zr和Ze分别为车轮的位移、车轮下钢轨位移与轨道不平顺；G为轮轨接触常数.当车轮处在钢轨节点时，Zr=Zri,Zri为钢轨梁单元节点i处垂向位移；当车轮处在钢轨节点之间时，用样条插值函数把钢轨相邻两节点上位移等效到车轮作用点处，Zr=H(Zri，Zrj)，Zri，Zrj分别为钢轨梁单元节点i，j处的垂向位移，H为插值函数.

由于钢轨通过梁单元来离散，其轮轨力作用时通过节点力来等效，其原理如图3所示.

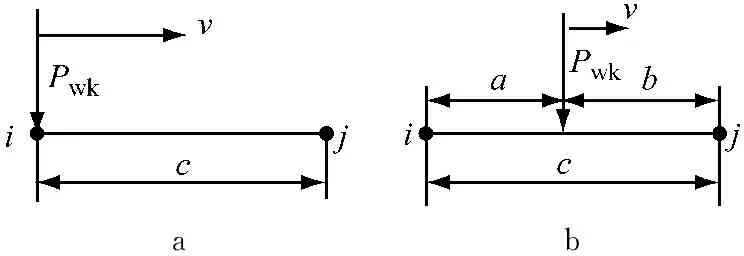
ab

图3 轮轨力等效到钢轨节点

Fig.3 Equivalent wheel rail force applied to rail nodes

当第k个车轮恰好处在钢轨节点i上，如图3a所示，那么轮轨力就等效在i节点上，则有

(4)

当第k个车轮处于钢轨两节点i，j之间，如图3b所示，那么轮轨力Pwk要分配到相邻节点i，j上.

(5)

(6)

(7)

(8)

综上所述，本文利用ANSYS中的APDL语言对车辆多刚体系统方程进行代码编写，选取新型快速显示积分法对车辆系统进行数值积分；对轨道-路基系统也采取同样的方法进行代码编写，选取隐式Newmark-β法求解；通过轮轨接触将车辆与轨道系统统一起来，通过数值积分实现车辆与轨道系统动力学响应的同步计算.

2 结果分析

2.1 参数选取

为研究重载列车作用下有砟轨道-路基系统动位移的空间分布，本文选取车辆-轨道-路基系统动力学参数如表1和表2所示，其中货车行驶速度为100 km·h-1，积分步长为0.0001 s.

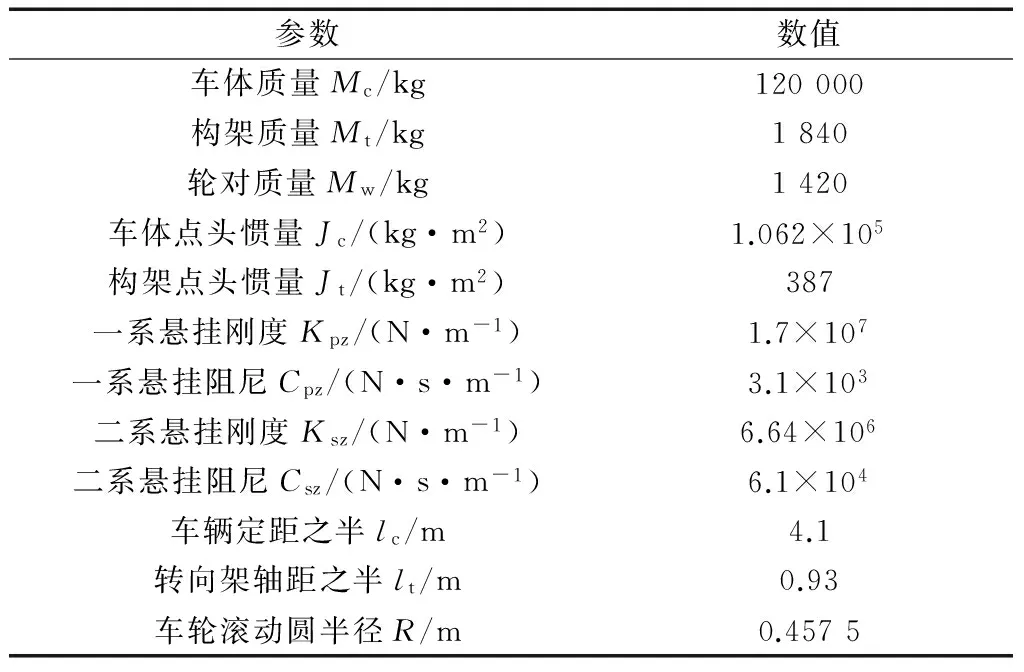
表1 30 t轴重货车车辆计算参数

轨道随机不平顺采取某重载铁路实测数据，以不平顺位移的形式输入计算，如图4所示.该不平顺数据能够考虑0.2 m以上波长的轨道随机不平顺.

2.2 模型验证

为验证上述模型的正确性，选择文献[21]中重载铁路轨道与路基计算结果进行对比分析，选取与文献[21]相近的动力学参数进行计算，将相同工况时的动力响应幅值对比如表3所示.

由表3可见，本文计算结果与文献[21]计算结果处于同一个数量级上，计算结果表明，轨枕加速度值略小，主要由轨枕结构的材料特性取值略有不同造成，其余数据指标与文献[21]相比误差均在5%以内，可见本文所建立模型的计算结果是准确可靠的.

表2 轨道路基系统模型参数

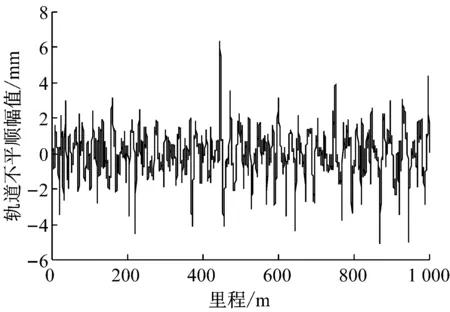
图4 本文计算所采用的轨道不平顺数据

Tab.3 Comparison of calculation results obtained in this paper and those given in[21]

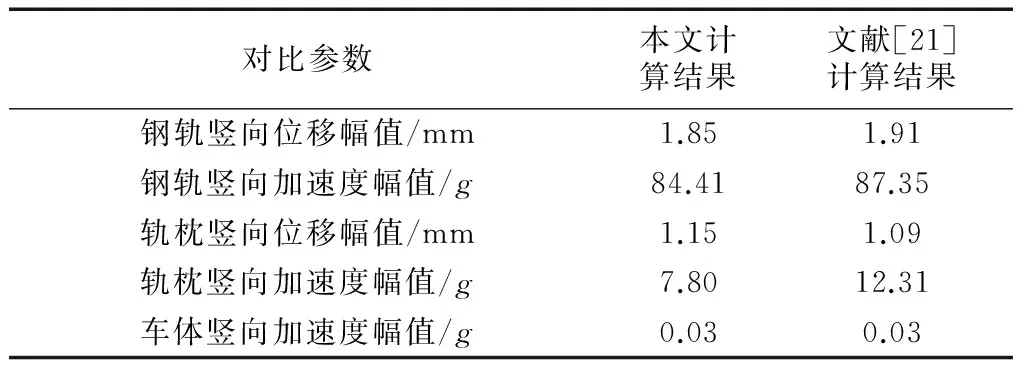
对比参数本文计算结果文献[21]计算结果钢轨竖向位移幅值/mm1.851.91钢轨竖向加速度幅值/g84.4187.35轨枕竖向位移幅值/mm1.151.09轨枕竖向加速度幅值/g7.8012.31车体竖向加速度幅值/g0.030.03

2.3 轨道动位移时程特性

选取道床表层上某一点，在荷载移动过程中，对其3个位移分量时程进行分析，如图5所示.图5中，U1，U2，U3分别对应于道床表层监测点纵向、竖向和横向的的动位移.

图5 道床表层监测点3个方向位移时程

由图5可知，纵向位移U1最大幅值为0.045 mm，竖向位移U2最大幅值为0.830 mm，横向U3最大幅值为0.017 mm.其中纵向最大动位移和横向最大动位移分别是竖向最大动位移的5.4%和2.0%.由此看出，3个分量中以U2为主，其他2个方向的分量在动位移的分析过程中的影响相对较小，因此在后续的动位移分析中，侧重于竖向动位移.

图6描述了0.5 s时刻道床表层竖向动变形的空间分布.

图6 道床层动位移

图7～10给出了某一时刻车辆下方道床和基床表层部分的动位移云图.

由图6～10可以看到，在所选取的道床、基床表层的断面测点上，在一节车厢通过的过程中大致会出现两次峰值，其峰值出现的时间节点分别对应于前后转向架通过的时间.

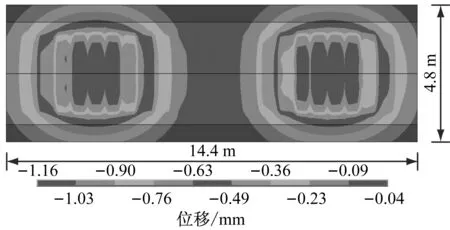
图7 轨枕下道床表层动位移云图

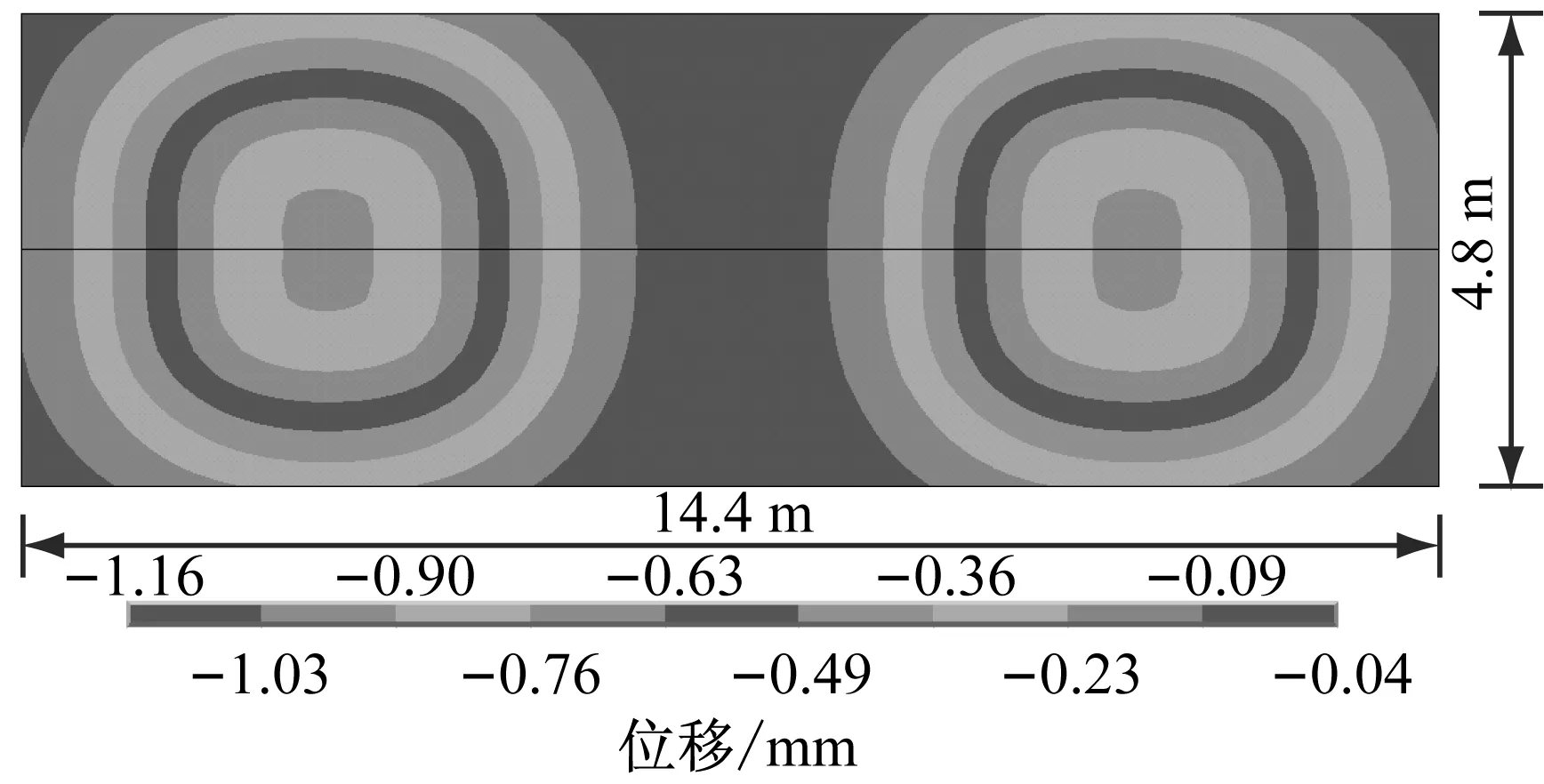
图8 道床底层下基床表层动位移云图

图9 钢轨下方道床及基床表层纵断面动位移云图

图10 钢轨及基床表层横断面动位移云图

2.4 竖向动位移沿横向分布规律

轨道-路基系统各阶层位置关系如图11所示.其中轨枕、道床面砟层、底砟层以及基床表层皆采用实体单元描述，而基床底层和下部结构采用弹簧单元进行等效模拟，并不进行分析计算.

如图11所示，取轨道-路基系统的一半对称结构进行分析，图中轨道-路基系统横断面的中心轴定为y坐标轴，监测点距轨道-路基系统横断面中心轴的距离定为x轴.轨道-路基系统基床表层及其上部结构等不同结构层竖向动位移沿横向的分布，如图12～15所示.

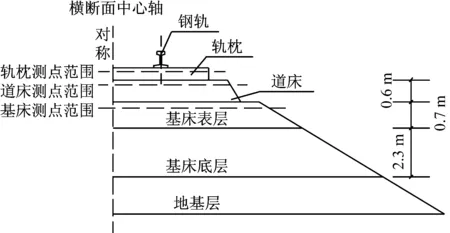
图11 轨道路基系统各结构层位置示意图

图12 轨枕中部竖向动位移分布

图13 道床面砟层竖向动位移分布

选取3个典型时刻，分析轨道-路基系统沿横向的竖向动位移的分布，其中0.407 9 s时刻竖向动位移出现峰值且为最大，0.703 0 s时刻竖向动位移也出现峰值且接近最大，0.451 8 s和0.623 0 s时刻则表示任意时刻.所取轨枕宽度为2.6 m，则半结构轨枕长度为1.3 m.从图12～15可以看出，在轨枕宽度范围内，沿横向，轨枕中部的竖向动位移的波动幅值为0.19 mm，道床面砟层竖向动位移的波动幅值为0.15 mm，道床底砟层竖向动位移的波动幅值为0.13 mm，基床表层竖向动位移的波动幅值为0.08 mm.

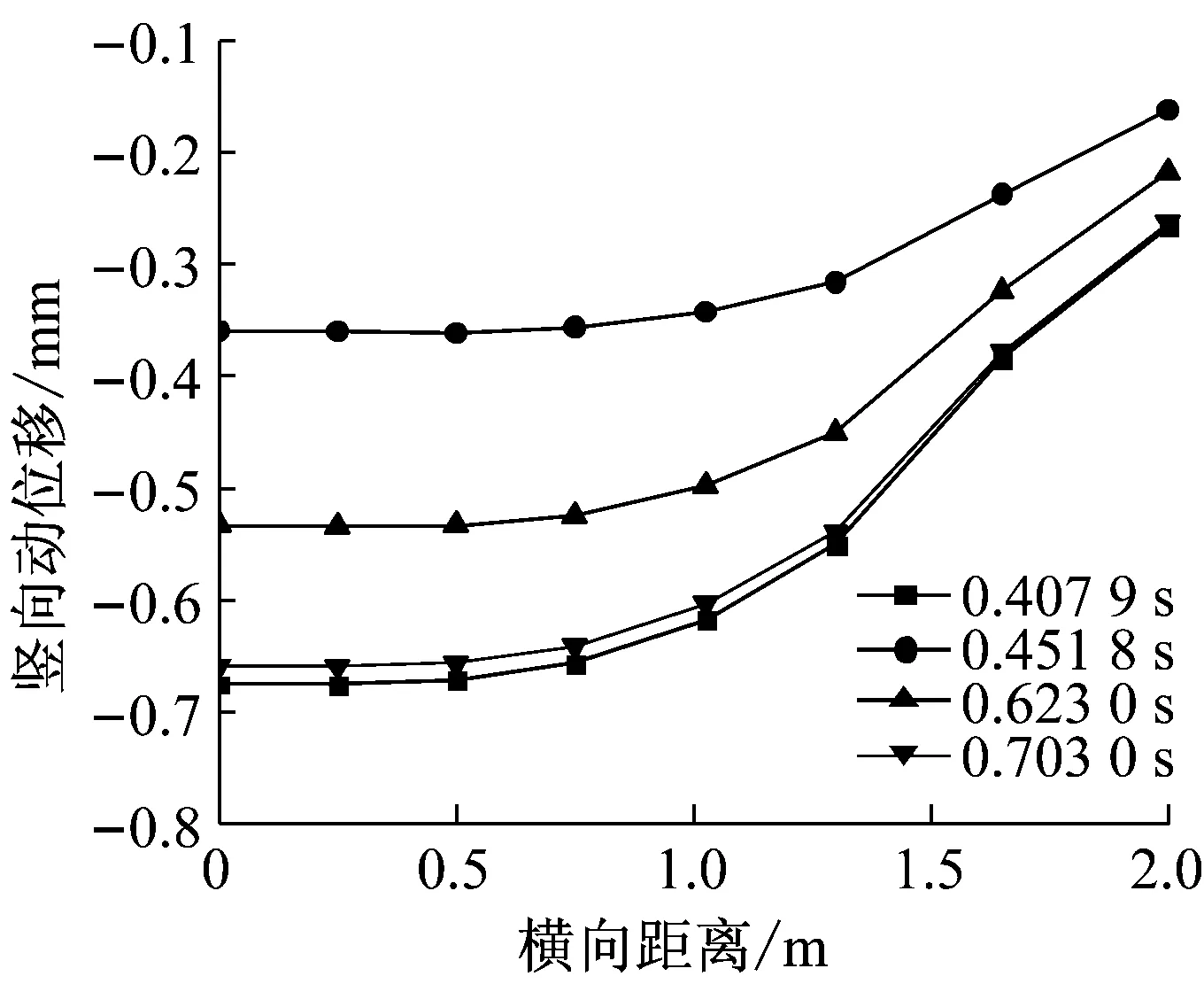
图14 道床底砟层竖向动位移分布

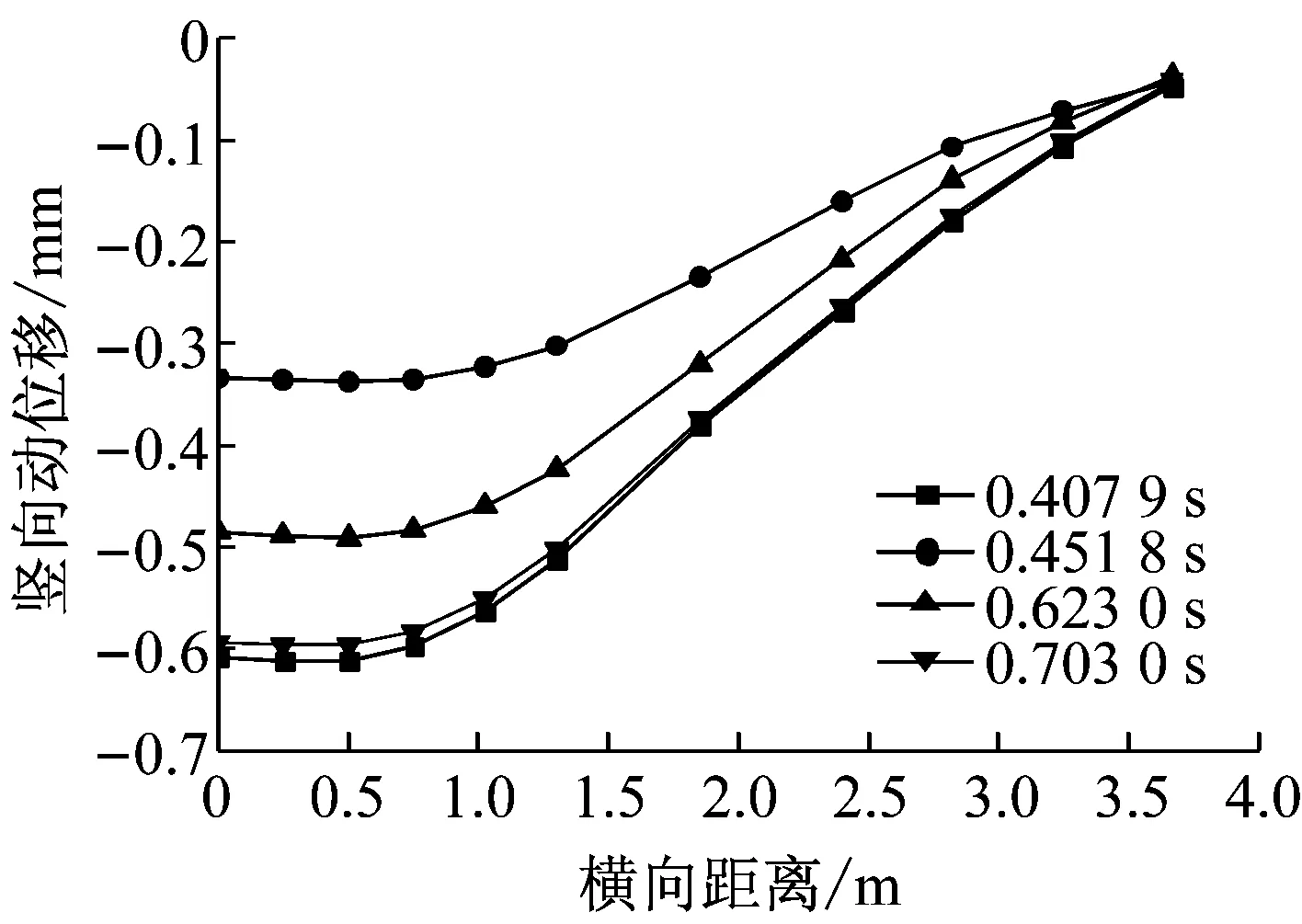
图15 基床表层竖向动位移分布

综上所述，轨道-路基系统竖向动位移沿横向的分布较为平缓，不同时刻分布形态相似，但有小幅波动，但最大波动值不超过0.2 mm，可近似看做平均分布.每一时刻最大动位移峰值出现在钢轨正下方区域，沿深度方向，轨道-路基系统最大竖向动位移出现在轨枕中部约为0.95 mm处，在容许范围内，满足正常使用要求.

2.5 竖向动位移沿竖向分布规律

钢轨下方不同时刻竖向动位移沿深度方向的分布如图16所示.由图16可知，不同时刻的竖向动位移沿深度的分布呈现相似的分布规律.钢轨竖向动位移最大值在0.4～1.9 mm之间，轨枕、道床、基床表层部分竖向动位移的最大值在0.3～1.0 mm之间.在钢轨与轨枕间动位移发生突变，这是由扣件和轨下胶垫的缓冲作用造成的.由于混凝土轨枕弹性模量较大，在轨枕高度的范围内，竖向动位移近似于维持不变.从道床层开始，竖向动位移开始减小，其减小速度沿深度方向不断衰减.

图16 不同时刻竖向动位移沿深度的分布

3 结论

基于车辆-轨道耦合动力学理论，采用有限元方法建立了重载货车-有砟轨道-路基系统耦合动力学模型，模型中充分考虑了机车车辆、有砟轨道和路基的相互耦合作用.利用新型快速显式积分法与Newmark隐式积分法相结合的数值仿真方法计算分析了在轨道不平顺激励下30 t轴重重载铁路轨道-路基系统动位移的分布规律.有如下结论：

(1)轨道-路基系统各结构层动位移状态较为复杂，在重载货车通过的过程中，所受荷载也处于循环往复的加载和卸载状态.

(2)在有砟轨道-路基系统的动位移3个分量中，竖向动位移的幅值较大，为0.83 mm，横向动位移以及纵向动位移的幅值均不超过竖向动位移幅值的6%；故重载货车经过引起的有砟轨道-路基系统动位移响应以竖向分量为主. 横向动位移的分布较为平缓，在轨枕层的波动最大，为0.19 mm，峰值出现在钢轨下方区域，基床表层及下部结构的动位移波动不超过0.08 mm.

(3)轨道-路基系统的竖向动位移变化，大体分为3个阶段.在钢轨到轨枕之间，出现明显突变，这是由于轨下胶垫的缓冲作用；在轨枕层区域的衰减幅度较小，这是由于轨枕的弹性模量较大；在道床层至基床表层及下部结构，竖向动位移表现为沿深度方向不断衰减，并且衰减速率随着深度的增加也在不断减小.

[1] Knothe K. Past and future of vehicle/track interaction [J]. Vehicle System Dynamic Supplement, 1995, 45(24): 1.

[2] Grassie S L. Review of workshop: aims open questions [J]. Vehicle System Dynamic Supplement, 1995, 45(24): 380.

[3] Powrie W, Yang L A, Clayton C R I. Stress changes in the ground below ballasted railway track during train passage [J].Journal of Rail and Rapid Transit, 2007, 221(2): 247.

[4] Yang L A, Powrie W, Priest J A. Dynamic stress analysis of a ballasted railway track bed during train passage [J]. Journal of Geotechnical and Geo-environmental Engineering, 2009, 135(5): 680.

[5] Sun Y Q, Dhanasekar M. A dynamic model for the vertical interaction of the rail track and wagon system [J]. International Journal of Solids and Structures, 2002, 39(5): 1337.

[6] 梁波,蔡英.不平顺条件下高速铁路路基的动力分析[J].铁道学报,1999, 21(2): 110.

LIANG Bo, CAI Ying. Dynamic analysis on subgrade of high speed railways in geometric irregularity condition [J]. Journal of the China Railway Society, 1999, 21(2): 110.

[7] 梁波,罗红,孙常新.高速铁路振动荷载的模拟研究[J].铁道学报, 2006, 28(4): 89.

LIANG Bo, LUO Hong, SUN Changxin. Simulated study on vibration load of high speed railway [J]. Journal of the China Railway Society, 2006, 28(4): 89.

[8] 高建敏,翟婉明,徐涌.有砟轨道下沉破坏变形参数影响分析[J].交通运输工程学报, 2007,7(4): 15.

GAO Jianmin, ZHAI Wanming, XU Yong. Analysis of parameters’ effects on settlement of ballasted track [J]. Journal of Traffic and Transportation Engineering, 2007,7(4):15.

[9] 高建敏,翟婉明.铁路有砟轨道下沉破坏进展[J].铁道学报, 2008, 30(5): 15.

GAO Jianmin, ZHAI Wanming. Advance in track settlement destruction of ballasted railway track[J]. Journal of the China Railway Society, 2008, 30(5): 15.

[10] 高亮,王璞,蔡小培,等.基于多车精细建模的曲线地段重载列车-轨道系统动力性能研究[J].振动与冲击,2014, 33(22): 1.

GAO Liang，WANG Pu，CAI Xiaopei，etal. Dynamic characteristics of train- track system in curved track sections based on elaborate multi-vehicle model [J]. Journal of Vibration and Shock, 2014, 33(22): 1.

[11] 王璞,高亮,蔡小培.重载铁路钢轨磨耗演变过程的数值模拟[J].铁道学报,2014, 36(10): 70.

WANG Pu, GAO Liang, CAI Xiaopei. Numerical simulation of rail wear evolution of heavy-haul railways[J]. Journal of the China Railway Society, 2014, 36(10): 70.

[12] 薛继连.30 t 轴重下朔黄铁路轨道结构强化技术试验研究[J].铁道学报,2015, 37(2): 70.

XUE Jilian. Experimental study on strengthening method of track structure for 30 t axle load in Shuo—Huang railway [J]. Journal of the China Railway Society, 2015, 37(2): 70.

[13] 薛继连.30 t 轴重下隧底密实度对隧底结构受力的影响及隧底加固效果分析[J].中国铁道科学,2015, 36(1): 90.

XUE Jilian. Analysis of the influence of tunnel bottom compactness on structure stress and strengthening measures under 30 t axle load train [J]. China Railway Science, 2015, 36(1): 90.

[14] 狄宏规,冷伍明,薛继连,等.朔黄铁路重载扩能的路基强度评估[J].铁道学报,2015, 36(8): 84.

DI Honggui, LENG Wuming, XUE Jilian,etal. Assessment of subgrade for transport capacity enlargement of Shuo—Huang heavy-haul railway [J]. Journal of the China Railway Society, 2015, 36(8): 84.

[15] 翟婉明.车辆-轨道耦合动力学[M].3版.北京:科学出版社, 2007.

ZHAI Wanming. Vehicle-track coupled dynamics[M]. 3nd ed. Beijing: China Science Press, 2007.

YANG Chunlei, LI Fu, FU Maohai,etal. Reasearch on the matching relationship between the axle[J]. China Railway Science, 2012, 33(3): 92.

[17] 刘信立.30 t及以上轴重货车动力性能仿真研究[J].铁道建筑技术，2013(10): 90.

LIU Xinli. Research on dynamic performance simulation of 30 t and above axle-load freght wagon [J]. Railway Construction Technology, 2013 (10):90.

[18] 耿志修,李学峰,张波.大秦线重载列车运行仿真计算研究[J].中国铁道科学, 2008, 29(2): 87.

GENG Zhixiu, LI Xuefeng, ZHANG Bo. Simulation study of heavy haul train operation on Datong—Qinhuangdao Railway [J]. China Railway Science, 2008, 29(2): 87.

[19] 王永成.既有铁路开行重载列车研究[J].交通运输工程与信息学报, 2014, 9(3): 64.

WANG Yongcheng. Research of heavy haul train operation on the existing lines [J]. Journal of Transportation Engineering and Information, 2014, 9(3): 64.

[20] 肖世伟,雷长顺.重载铁路路基荷载特征和路基动力响应分析[J].铁道工程学报, 2014, 4(4): 51.

XIAO Shiwei, LEI Changshun. Loading characteristics and dynamic response analysis of subgrade for heavy haul railway [J]. Journal of Railway Engineering Society, 2014, 4(4): 51.

[21] Jin Shi, Andrew H Chan, Michael PN Burrow. Influence of unsupported sleepers on the dynamic response of a heavy haul railway embankment [J]. Journal of Rail and Rapid Transit, 2013, 227(6): 657.

Spatial Distribution Characteristics of Displacement of Heavy Haul Railway Ballasted Track-Subgrade System Under 30 t Axle Freight Vehicle Running

YANG Xinwen, LONG Tianhang, ZHOU Shunhua

(Key Laboratory of Road and Traific Engineering of the Ministry of Education, Tongji University, Shanghai 201804, China)

A dynamical interaction model of the ballasted track, subgrade and heavy haul train system was developed. The distribution of displacement of the heavy haul railway ballasted Track-subgrade system under 30 t axle freight vehicle running are solved using the combination of the new rapid explicit integration method and the Newmark integration method. The results show that the dynamical displacement state of each structure layer of the track-subgrade system is complex, and the load is in the cyclic loading and unloading during heavy haul vehicle passing. The amplitude of vertical dynamic displacement is the largest in three components of the displacement of the track-subgrade system, while the amplitude of the lateral displacement and longitudinal displacement are less than 6% of the amplitude of the vertical dynamic displacement. The dynamic displacement distribution in lateral direction, of which the amplitude fluctuation is less than 0.2 mm, is relatively moderate and could be approximated as uniform distribution. The changes of the dynamic displacement of the track-subgrade system in vertical direction could be divided into three phases: for the first part between the rail and the sleeper, the amplitude of dynamic displacement attenuates distinctly; for the second part, the amplitude of dynamic displacement attenuates gently in the sleeper region; and for the third part under the ballast bed, the amplitude of dynamic displacement attenuates continuously along the vertical direction, and the rate of attenuation is continuously decreasing with the increase of the depth.

heavy haul railway; ballasted track; subgrade; dynamic displacement; spatial distribution

2016-01-04

国家自然科学基金(51378395)；牵引动力国家重点实验室开放课题(TPL1602)

杨新文(1973—)，男，副教授，博士生导师，工学博士，主要研究方向为轨道交通振动与噪声，车辆-轨道耦合动力学.

E-mail：xinwenyang@tongji.edu.cn

周顺华(1964—)，男，教授，博士生导师，工学博士，主要研究方向为岩土工程和铁道工程.E-mail:zhoushh@tongji.edu.cn

TB533.1；U270

A