基于因果关系的列控系统模型约简方法

周庭梁， 许 婧， 陈小红， 赵时旻

(1.同济大学 道路与交通工程教育部重点实验室， 上海 201804；2.卡斯柯信号有限公司， 上海 200071;3.华东师范大学 上海市高可信计算重点实验室, 上海 200062)



基于因果关系的列控系统模型约简方法

周庭梁1,2， 许 婧2， 陈小红3， 赵时旻1

(1.同济大学 道路与交通工程教育部重点实验室， 上海 201804；2.卡斯柯信号有限公司， 上海 200071;3.华东师范大学 上海市高可信计算重点实验室, 上海 200062)

在基于安全需求对验证问题进行投影的方法基础上，针对投影出的验证子问题，提出了基于因果关系的变量约简方法，定义了环境变量间的因果关系，归纳出基本的因果关系组合，并提炼出变量约简规则，通过变量约减减少了验证问题的状态空间.采用国内某地铁线路的相关数据进行建模和验证，结果表明，该方法能够有效降低系统验证复杂度.

需求验证； 变量约简； 因果关系； 列车运行控制系统

作为一种安全攸关系统，列车运行控制系统(简称列控系统)必须经过验证.目前列车运行控制系统的建模和验证方法主要有以下3种：① 基于逻辑的方法.这类方法基于集合论和一阶逻辑，采用逻辑推理或者定理证明的方式精化系统的功能，证明系统的正确性，典型代表是Z，VDM，B和Event-B方法[1]等，其中B方法已经在法国巴黎RER线路所采用的SACEM系统[2]中得到成功应用.② 基于进程代数的方法.进程代数关注并行行为，强调对不同模块并发过程之间的交互进行建模.例如，Zou等[3]调研了如何对CTCS-3(Chinese Train Control System 3)的系统需求规约(system requirement specification，SRS)进行形式化的描述和验证.③ 基于形式化模型与规约的方法.在列控系统的需求阶段，多种类型的模型被用于系统建模和验证过程中.例如，基于有色Petri网(coloured Petri nets，CPNs)，Horste等[4]对欧洲列控系统ETCS进行了针对系统功能的形式化描述.

虽然现有的这些需求建模方法能有效避免二义性，并且能成功实现对需求规约的验证，但是这些方法并没有考虑到环境的影响.列控系统所处环境的复杂性以及环境自身的其他特性，会带来系统模型验证空间急剧爆炸的问题，导致在复杂环境中难以保证系统的可信度.因此，在需求模型的可信构造和验证过程中，需要研究如何对环境相关的约束进行调整，从而提高复杂环境下列控系统模型的可验证性.

为了解决这个问题，组合验证方法应运而生[5].组合验证方法先将系统分解为子系统，然后分别验证各子系统，最后分析集成的系统.这类方法在很多大型系统中得到成功的应用，例如McMillan[6-7]将该方法应用于微处理器的乱序执行单元和多处理机的缓存一致性协议.但是传统的组合验证的分解方法只能对系统进行划分，不允许子系统中存在重叠的部分.然而在列控系统中，由于环境共享，不可避免地存在子系统之间的部分重叠.基于问题框架方法的投影[8]是一种有效的处理有重叠部分的分解方法.它能够对复杂的问题通过投影进行分解，降低大型系统的复杂度.

基于问题框架方法，本文作者提出了一种基于安全需求的验证问题投影方法[9]，以列车控制验证系统的安全子属性作为投影维度，将列控系统验证问题投影为若干子问题.该方法可以有效地降低复杂度，但还是不能完全避免验证问题状态空间过大的问题.在研究投影出的子问题时，发现在列控系统中，变量之间存在因果关系，而变量的减少可以有效减小状态空间.因此，本文通过找出存在因果关系的变量，并根据不同的因果关系类型对这些变量进行约简，进一步降低验证系统的状态空间.最后采用国内某地铁线路的相关数据进行建模和验证，结果表明，该方法可以有效地降低验证系统的复杂度，降低形式化模型验证中的状态空间爆炸问题发生的可能性，并且提升了形式化验证的效率.

1 列控系统的需求模型验证问题及投影

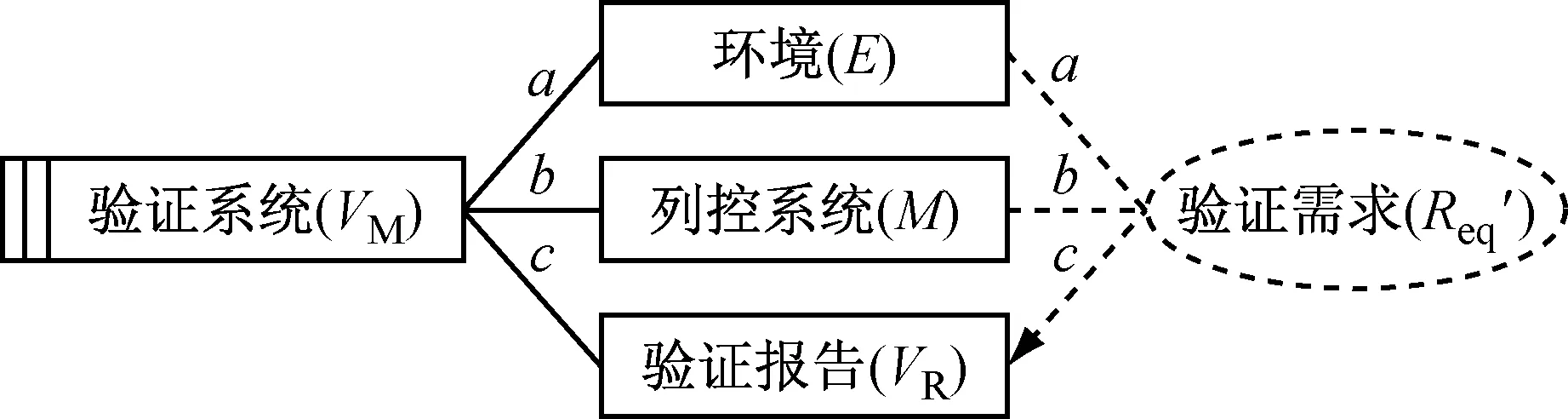
IS=a∪b∪ca:E!{p11,p12,…,pnm}b:M!{q11,q12,…,qnm}c:VM!{true, false}

图1 列控系统验证问题

Fig.1 Verification problem of automatic train

control system

在这些元素中，环境(E)实际上是与列控系统进行交互的设备集合，每个设备可以用一组变量描述.因此，本文将E定义为一组设备变量Di(0≤i≤n)的集合，而每个设备变量又有一组属性变量Vij(0≤i≤n,0≤j≤m)表示，可形式化定义为E={D1,D2,…,Di,…,Dn}，其中，Di={Vi1,Vi2,…,Vij,…,Vim}.

E与M有共享的交互集合a和交互集合b，其中a为由E控制的交互pij(0≤i≤n,0≤j≤m)的集合，b为由M控制的交互qij(0≤i≤n,0≤j≤m)的集合.在列控系统问题中，因为E和M间共享的是设备的属性变量，所有的交互都是值交互，所以可以将交互定义为由设备的属性变量的取值所确定的函数值，因此将与设备Di的属性变量有关的交互pij,qij定义为，pij=fij(Vi1,Vi2,…,Vim)，qij=gij(Vi1,Vi2,…,Vim).

安全需求(Req)描述了M需要满足的条件.Req引用了交互b，这是一个约束引用，约束环境的行为必须按照安全需求所规定的方式改变.安全需求由一组安全属性构成，只有当每个安全属性Pi(0≤i≤n)都成立时，安全需求Req才能成立.安全需求定义为(其中∧表示与)：Req=P0∧P1∧…∧Pi∧…∧Pn.

在这些定义基础上，提出了基于安全需求对列控系统的验证问题进行投影[9]，将原验证问题投影成多个子问题进行验证，从而得到了新的子问题的验证系统、验证环境和验证需求.由于安全需求Req与问题的5个描述元素都有关系，所以可将Req作为投影的维度.因此，可以基于安全子属性对整个验证问题进行投影.采用关系代数类似的表达，问题投影的形式可以表示如下：

(1)

在这4个辅助算子的基础上，结合系统M，可以定义列控系统形式化验证问题的投影为

(2)

在对投影结果进一步分析时发现，在对子问题的环境进行投影时只是将与待验证的安全需求无关的设备进行约简，保留下所有与待验证的安全需求相关的设备参数.因此，只要与待验证的安全需求产生了交互，该设备的所有变量都会被加入到环境中，但并不是所有加入的变量都真正会对验证结果产生影响.因此，本文提出基于因果关系的约简方法，尝试找出设备内部的各个变量间可能存在的关系，并基于变量间的因果关系进一步降低系统的复杂度，从而进一步减小系统的状态空间，提高系统的验证效率.

2 基于因果关系的变量约简

2.1 列控系统的变量因果关系分析

在对列控系统验证问题进行投影后，将原验证问题投影成多个子问题进行验证，能有效地降低系统验证复杂度[11].但在投影后，只要与验证需求产生了交互，该设备的所有变量都会被加入到环境中.但事实上，并不是所有变量都会对验证结果产生影响[12]，这为进一步约简验证系统提供了可能.

在未对变量进行任何约简前，环境中所有设备的属性变量都与验证系统共享.分析各变量间的关系后可以发现，在某些设备内部的变量之间存在直接的因果关系.

设C,R为E中的变量或者E中变量间任意的与、或组合.根据因果关系理论，因果关系共分为4种：①C→R；② ￢C→R；③C→￢R；④ ￢C→￢R.

在情况①中，即当C存在时，R一定存在，且R可由C推导得出，因此可设R=S(C)，此时可直接用C来表示R.

例如，在描述列车车尾的位置时，有两个变量：最大车尾MaxTrainTailPos和最小车尾MinTrainTailPos.最大车尾和最小车尾之间的距离固定为TailLength，所以有

MaxTrainTailPos=MinTrainTailPos+

TailLength

则MinTrainTailPos → MaxTrainTailPos可表示为MaxTrainTailPos = S(MinTrainTailPos).

此时，所有与MaxTrainTailPos相关的变量均可由S(MinTrainTailPos)替代.

在情况②中，当C不存在时，R一定存在.在情况③中，当C存在时，R一定不存在.在列控系统的环境中，设备的属性变量很少出现互斥的关系，所以在列控系统中，这两种因果关系很少存在.即使存在，在情况②中，由于C不存在，R无法由C推导得出，所以无法约简.在情况③中，由于R本身就不存在，所以同样无法约简.在情况④中，当C不存在时，R一定不存在.这种情况下，由于C，R都不存在，这种因果关系对约简状态空间没有实际意义.

总结上述4种情况分析, 只有C→R这类因果关系会对列控系统验证过程中的变量约简产生直接影响.由于系统验证时会对所有变量进行全状态空间的遍历，可用R=S(C)替代R，在R的取值范围较大的情况下可明显减小状态空间，提升系统的验证效率.由于变量的因果关系不一定是一一对应的，也可能存在多个变量之间的因果关系.设C,R为E中的变量或者E中变量间任意的与、或组合，由上文可知，只有C→R类因果关系能用于变量约简.

2.2 列控系统的因果关系定义

为了表达出所有能用于变量约简的因果关系，基于巴克斯范式(Backus-Naur Form，BNF)[13]对比类因果关系进行如下定义：

<因果关系> ::= <变量表达式> → <变量表达式>

<变量表达式> ::= <变量> | <变量表达式> <运算符> <变量表达式>

<运算符> ::= ∧ | ∨

<变量> ::=V1|V2|…|Vi| …|Vn

变量间的组合型因果关系有7种最基本的情况，设Vi,Vj,Vk,Vl∈E，这7种基本情况分别为

(3)

(1)Vi→Vl

由上文可知，这种情况下可以用Vl=S(Vi)替代Vl.

(2)Vi∧Vj→Vl

需要同时知道Vi和Vj，才能推导出Vl.这种情况下Vl可表示为Vl=S(Vi,Vj).

(3)Vi∨Vj→Vl

只需知道Vi和Vj中任意一个变量，就能推出Vl.这种情况下Vl可表示为Vl=S(Vi)或Vl=S(Vj)，从中任取一种即可.从变量约简的角度看，替换Vl时选择Vi和Vj没有区别，所以可以比较Vl=S(Vi)和Vl=S(Vj)，从中选择较为简单的一种表示方法对Vl进行替换.

这种情况下，需要知道Vi∧Vj或者Vl，就能推出Vl.则Vl可表示为Vl=S(Vi,Vj)或Vl=S(Vk)，从中任取一种即可.由于Vl=S(Vk)的表示方法更简洁，用S(Vk)替换Vl会使之后的验证过程更为简单.

这种情况下，需要知道Vi∧Vk或者Vj∧Vk，才能推出Vl.所以Vl可表示为Vl=S(Vi,Vk)或Vl=S(Vj,Vk)，从中任取一种即可.

(6)Vi→Vj∧Vl

在这种情况下，只需知道Vi，就可以推出Vj和Vk，因此等价于Vi→Vj且Vi→Vk.

(7)Vi→Vj∨Vl

在这种情况下，因无法确定推出的结果是Vj还是Vk，所以无法进行约简.如果有其他信息能辅助判断推出的结果具体为哪个变量，则可以将问题转化为Vi→Vj或者Vi→Vk进行处理.

2.3 变量表达式的约减规则

在提炼出的7种基本情况中，情况(1)是一对一的情况，即一种原因推出一个结果；情况(2)至(5)是多对一的情况，即多种原因可以推出一个结果.这5种情况中变量Vl都可以由其他变量推出，因此可以用其他变量进行替代.情况(6)和(7)是一对多的情况，用一个变量能够推导出多个结果，即变量Vj和Vk都可以用变量Vi推导得到，因此在变量约简后，可以用更少的变量来定义交互，由此可以降低验证复杂度.除了上述7种最基本的情况外，式(3)所定义的其他情况都是这7种情况的组合，并可以通过依次迭代最终化简为这7种情况中的一种，再对变量进行约简.

设C,C1,C2,C3,R,R1,R2是式(3)所定义的变量表达式，通过对这7种最基本情况的分析，可以总结出4个约简规则：

(4)

根据基本情况(3)可知，只需知道C1和C2中任意一个变量表达式，就能推出R，所以原因中的C1∨C2可以直接用C1或C2替换.

(5)

根据基本情况(6)可知，只需知道C，就可以推出R1和R2，因此等价于C→R1且C→R2，可以拆成这两种情况分别进行讨论.

(6)

根据基本情况(4)可知，只需要知道C1∧C2或者C3，就能推出R.由于用C3推导R会更为简洁，所以 (C1∧C2)∨C3直接用C3替换.

(7)

根据基本情况(5)可知，只需要知道C1∧C3或者C2∧C3，就能推出R.所以(C1∨C2)∧C3可用C1∧C3或者C2∧C3替换.

在对列控系统的变量进行分析时，如果变量之间存在可以用于约简的因果关系，则一定在式(4)所定义的范围内.而式(4)所定义的因果关系，又可以通过上述4个化简规则转化成最基本的7种变量间的组合型因果关系之一进行处理，所以对所有可能情况都可以进行相应的变量约简操作.在约简的过程中，由于交互并未发生改变，但验证过程中实际使用到的变量个数减少了，从而降低了系统验证复杂度.

3 实例分析

以卡斯柯信号有限公司的轨旁列控系统区域控制器iZC为例，应用基于因果关系的约简方法，降低系统验证的复杂度.与上一代列控系统有所不同，CBTC系统通过移动闭塞来追踪并保护列车.iZC根据轨道上各列车的精确位置，来计算各列车之间的安全区间，并通过无线车地通信传递给列车.这些安全区间被称为移动授权(MA).MA属于列控系统的核心安全功能，其安全等级达到SIL4要求，必须通过形式化验证来确保该功能的正确性及安全性.

iZC会在每个计算周期内为其管辖范围内的所有列车计算移动授权MA的范围，起点一般为列车的最小车头，计算得到的终点称之为EOA(end of authority).EOA是指授权列车移动的最大距离，EOA的计算依赖于列车自身的位置、速度，同时还依赖于轨道上的信号设备和特殊区段，例如包括信号机、缓冲区、重叠区等.

根据IEEE 1474.1标准[14]，当遇到8种特殊情况时列车EOA计算将会终止，例如列车前方出现另外一辆CBTC列车、缓冲区、重叠区等等.这些情况可能导致列车运行发生事故，因此这些情况也被称为非安全状态点.根据这8种情况，本文将EOA分为8种类型.同时，在iZC发给列车的MA报文中，包含EOA_TYPE字段，主要描述选取当前点作为EOA的原因.

3.1 EOA验证问题描述

EOA模型的形式化验证问题可以表示为:

ProblemEOA=

其中，EOA为待验证的系统模型，共有8种类型，在验证过程中为“黑盒”，不可更改.EnvEOA为问题所处的环境，包含车、闭塞、分支、信号机、BZ(buffer zone)、OL(overlap)、TD(traffic direction)等，即

EnvEOA=

VeriEOA为需要创建的EOA验证系统.IntEOA为EnvEOA与各问题领域交互的集合Int1∪Int2∪Int3.SafeR′为EOA的验证需求，验证EOA的安全需求SafeR=P0∧P1∧P2.

针对不同的EOA系统类型j，每个安全需求Pi仅需满足对应的安全子属性Pij，因此有

SafeR=P01∧P02∧…∧P08∧P11∧…∧P18∧P21∧…∧P28

由于系统EOA不可变动，所以投影后结果不会变化.另外的4个元组可以借助投影算子分别进行投影.下面以第8种类型EOA为例进行投影，并对投影后的子问题进行约简.该类型EOA表示非安全状态点为重叠区，即前方搜索到闭塞轨道边界.根据文献[9]中的投影方法，以安全子属性SafeR8为投影维度，对 ProblemEOA进行投影，投影结果为

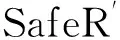
SProblemEOA8是由原问题ProblemEOA投影出的子问题.安全需求SafeR8是原问题安全需求SafeR的子集，验证时可直接跳过与当前类型无关的安全需求的验证过程，因此，根据投影后的安全需求设计出的验证系统的规模也相应减小.

3.2 EOA验证变量约简

列控系统一般采用两种坐标定位方式.一种是基于闭塞(block)的，例如一组道岔的位置可以表示为一个二元组(Block_Index, OffsetOnBlock)，其中Block_Index表示道岔所处的闭塞索引，OffsetOnBlock表示精确的位置偏移.另外一种是基于分支(branch)的，分支是一组闭塞连接而成的连续轨道，一组道岔的位置可以表示为一个二元组(Branch_Index, OffsetOnBranch)，其中Branch_Index表示道岔所在的分支索引，OffsetOnBranch表示在该分支上的精确的位置偏移.因此，所有的基于闭塞的位置坐标都可以转化为基于分支的位置坐标.

以列车内部变量关系为例，列车位置由4个坐标决定：最大(MaxTrainHeadPos)/最小(Min-TrainHeadPos)车头位置和最大(MaxTrain-TailPos)/最小(MinTrainTailPos)车尾位置.值域[MinTrainHeadPos, MaxTrainHeadPos]代表列车车头的可能位置.值域[MinTrainTailPos, Max-TrainTailPos]代表列车车尾的可能位置.同时，每辆列车被一个列车在轨道上的虚拟占用区域(VTP)包络.iZC系统被设计用于计算VTP的碰撞概率，并防止这些VTP发生碰撞.由于VTP的位置与列车的位置相互关联，VTP的位置变量与列车的位置变量会相互影响.VTP位置也由4个坐标决定：最大(MaxVTPHeadPos)/最小(MinVTPHeadPos)VTP头位置和最大(MaxVTPTailPos)/最小(MinVTP-TailPos)VTP尾位置，如图2所示.

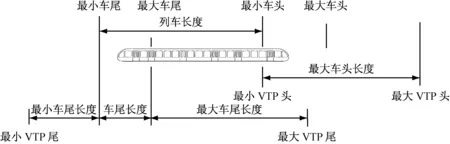
图2 列车定位相关坐标点

另外还有1个列车状态变量(TrainMonitor-Modes)用来表示列车当前的运行模式.由此可知，

Train={MinVTPTailPos, MaxVTPTailPos,

MinVTPHeadPos, MaxVTPHeadPos,

MinTrainTailPos, MaxTrainTailPos,

MinTrainHeadPos, MaxTrainHeadPos,

TrainLength, TrainMonitorModes}

在问题投影过后生成的子问题SProblemEOA8中，列车的位置坐标点全部随机，即它们可能为任意一个block中的任意一个点.但实际情况中，车的位置坐标之间存在几组等价关系，由图2可以推导出：

(1) 最小VTP尾与最小车尾间距离为固定值MinTailLength，所以

MinTrainTailPos → MinVTPTailPos

(2) 最小车尾与最小车头之间距离为固定长度，所以

MinTrainTailPos∧MinTrainHeadPos→

TrainLength

(3) 最小车头与最小VTP头的位置一致，所以

MinTrainHeadPos → MinVTPHeadPos

(4) 最大VTP头与最小VTP头间距离为固定值MaxHeadLength，所以

MinVTPHeadPos→MaxVTPHeadPos

又因为MinTrainHeadPos→

MinVTPHeadPos

所以

MinTrainHeadPos→MaxVTPHeadPos

(5) 最大车尾与最小车尾间距离为固定值TailLength，所以

MinTrainTailPos → MaxTrainTailPos

(6) 最大车尾与最大车头间距离为车长，所以

MaxTrainTailPos∧TainLength→

MaxTrainHeadPos

又因为MinTrainTailPos → MaxTrainTailPos

MinTrainTailPos∧MinTrainHeadPos→

TainLength

所以

MinTrainTailPos∧MinTrainHeadPos→

MaxTrainHeadPos

(7) 最大车尾与最大VTP尾间距离为固定值MaxTailLength，所以

MaxTrainTailPos → MaxVTPTailPos

又因为MinTrainTailPos → MaxTrainTailPos

所以

MinTrainTailPos → MaxVTPHeadPos

由此，一旦确定了最小车尾和最小车头的具体坐标，就能得到车长，另外6个列车的相关坐标点位置也能相应固定.所以Train可以约简为

Train′={MinTrainTailPos,

MinTrainHeadPos, TrainMonitorModes}

此时，Train中的10个变量可约简为Train’中的3个变量，系统验证状态空间得到了极大的约简，有效降低了验证复杂度.

3.3 EOA验证实验及分析

以图3所示的国内某地铁线路数据作为环境，线路中共有6个block，并涵盖2个道岔.在此环境下，基于SCADE工具直接对iZC系统模型进行验证.

图3 验证环境

按照文献[5]中的投影方法，基于安全需求对验证问题进行投影后， iZC系统顺利通过了形式化验证.图4展示了投影生成的SProblemEOA8的验证结果.由图4的结果可以看出，复杂环境下系统验证状态空间仍然较大，形式化验证耗时较长.

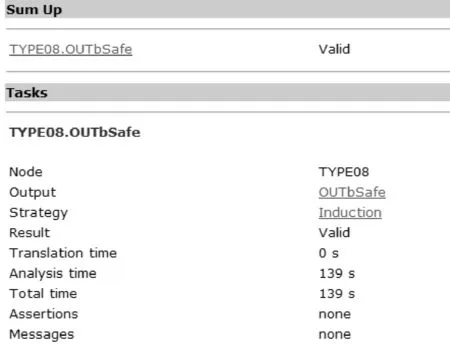
图4 投影后系统的验证结果

按照第2节中的约简方法，基于因果关系对变量进行约简后，环境输出的变量减少，系统的复杂度进一步降低，状态空间进一步缩小，形式化验证的效率得到提高.由于消耗时间可能与工具运行状态有关，可能存在一定的随机性，所以每种类型在约简前后均多次验证，最终结果取多次验证所耗时间的平均值进行分析.变量约简前后每种类型的待验证系统进行验证所耗的时间如图5所示.

图5 变量约减前后验证效率对比

由实验结果可知，对于系统过于复杂，验证时间较长的iZC系统，在对每种类型的验证子系统分别进行验证时，基于因果关系对变量进行约简，使验证所需的时间缩短，验证效率得到了有效提高.由此在对整个iZC系统进行验证时，所需的总体时间明显缩短，验证效率显著提升.

4 结论

本文针对列控系统的特点，在对列控系统进行形式化验证的过程中，提出可以利用列控系统各设备变量间的因果关系对验证系统进行化简，形成基于因果关系的列车运行控制系统模型约简方法.通过分析变量间的因果关系，在基于安全需求的列控系统投影方法的基础上，针对投影得到的子系统，根据设备内各变量之间存在的因果关系进一步对环境的输出变量进行了约简，从而减少了验证系统的状态空间.

本文以轨旁列控系统iZC的安全功能EOA为例，进行EOA形式化验证问题的投影及变量约减，并对8种EOA类型的验证子系统分别进行验证.实验结果表明，采用基于因果关系的列控系统模型约简方法，能够有效地提高形式化验证的效率.

[1] Abrial J R. Modeling in Event-B: system and software engineering[M]. New York: Cambridge University Press, 2010.

[2] DaSilva C, Dehbonei B, Mejia F. Formal specification in the development of industrial applications: subway speed control system[C]//Proceedings 5th IFIP Conference on Formal Description Techniques for Distributed Systems and Communication Protocols (FORTE’92). North-Holland: Perros-Guirec, 1993:199-213.

[3] Zou L, Lv J, Wang S,etal. Verifying Chinese control system under a combined scenario by theorem proving [C]//International Conference on Verified Software: Theories, Tools, Experiments (VSTTE). Berlin: Springer-Verlag, 2013: 262-280.

[4] Horste M, Hungar A, Schnieder E. Modelling functionality of train control systems using petri nets[R]. Madrid: FM-RAIL-BOK Workshop, 2013.

[5] Giannakopoulou D. Model checking for concurrent software architectures[D]. London: University of London, 1999.

[6] McMillan K L. Microarchitecture verification by compositional model checking[C/CD]∥Proceedings of the 13th International Conference Computer-aided Verification. Livingston: Springer-Verlag, 2011.

[7] McMillan K L. Parameterized verification of the FLASH cache coherence protocol by compositional model checking[C/CD]∥Correct Hardware Design and Verification Methods. Lecture Notes in Computer Science. Livingston: Springer-Verlag, 2001.

[8] JIN Zhi, CHEN Xiaohong, Zowghi Didar. Performing projection in problem frames using scenarios[C]//16th Asia-Pacific Software Engineering Conference. Piscataway: IEEE, 2009: 252-256.

[9] XU Jing, CHEN Xiaohong, ZHOU Tingliang, et al. Decomposing automatic train control verification system with projection[C]//22th Asia-Pacific Software Engineering Conference. Los Alamitos: IEEE Computer Society, 2015: 301-308.

[10] 陈小红，尹斌，金芝. 基于问题框架方法的需求建模：一个本体制导的方法[J]. 软件学报，2011, 22(2): 177.

CHEN Xiaohong, YIN Bin, JIN Zhi. Ontology-guided requirements modeling based on problem frames approach [J]. Journal of Software, 2011, 22(2): 177.

[11] Sanaz Yeganefard, Michael Butler. Problem decomposition and sub-model reconciliation of control systems in Event-B[C]//IEEE 14th International Conference on Information Reuse & Integration (IRI). Piscataway: IEEE, 2013: 528-535.

[12] Alebrahim Azadeh, Faβbender Stephan. Problem-based requirements interaction analysis[C]//20th International Working Conference. Cham: Springer International Publishing, 2014: 200-215.

[13] Backus J W. The syntax and semantics of the proposed international algebraic language of the Zurich ACM-GAMM Conference[C]//Proceedings of the International Conference on Information Processing. Paris: UNESCO, 1959: 125-132.

[14] IEEE. IEEE Std 1474.1 Standard for communications-based train control (CBTC) performance and functional requirements[S]. [S.l.]: IEEE, 2004.

Automatic Train Control System Model Reduction Based on Causal Relation

ZHOU Tingliang1,2, XU Jing2, CHEN Xiaohong3,ZHAO Shimin1

(1.Key Laboratory of Road and Traffic Engineering of the Ministry of Education, Tongji University,Shanghai 201804, China; 2.CASCO Signal Ltd., Shanghai 200071, China; 3. Shanghai Key Laboratory of Trustworthy Computing, East China Normal University, Shanghai 200062, China)

Based on the previous work about verification problem projection according to the safety requirements, a variable reduction approach was proposed based on causal relation for the projected sub-problems. First, the causal relations among the environment variables of the projected sub-problems were defined. Then, the basic causal relation combination of variables and the reduction rules were concluded. Through variable reduction, the state space of the verification problem was reduced. Finally, with configuration of a domestic metro line, an experiment of modeling and verification was demonstrated to show that the variable reduction approach efficiently reduces the verification complexity.

requirement verification; variable reduction; causal relation; automatic train control system

2016-03-29

国家自然科学基金(91418203)

周庭梁(1980—)，男，博士生，主要研究方向为轨道交通列车列控系统研制、测试及安全评估.E-mail:Leon_ztl@163.com

TP311

A