降雨条件下城市快速路车速模糊神经网络预测方法

孙洪运， 杨金顺， 李林波， 吴 兵

(1.同济大学 道路与交通工程教育部重点实验室，上海 201804；2.青岛理工大学 汽车与交通学院，山东 青岛 266555)



降雨条件下城市快速路车速模糊神经网络预测方法

孙洪运1， 杨金顺2， 李林波1， 吴 兵1

(1.同济大学 道路与交通工程教育部重点实验室，上海 201804；2.青岛理工大学 汽车与交通学院，山东 青岛 266555)

为了提高降雨条件下快速路车速短时预测的准确性，考虑到各影响因素的模糊性以及影响作用非线性变化特点，提出了一个以交通量、占有率和降雨量为输入，以车速为输出的模糊神经网络预测方法.利用上海市快速路的交通流与气象数据确定了最优模型结构，并与自回归积分滑动平均模型、反向传播神经网络模型和支持向量机模型进行对比分析.该方法的预测均方根误差为3.05 km·h-1，预测平均误差为3.95%，均优于其他3种方法.

快速路； 车速预测； 模糊神经网络； 交通状态； 降雨

车速是宏观交通流参数之一，是计算道路行程时间和评价交通拥挤的基础，也是主动交通管理和出行信息发布的依据，因此准确预测车速的重要性不言而喻.居民出行和交通运输都是暴露在自然环境之下的，难免不受恶劣气象条件的干扰.特别在日益频繁的强降雨条件下，较小路面摩擦系数和较低能见度条件改变了降雨天快速路交通流特性，比如自由流车速下降、运行速度方差增大、交通流量-密度-速度三参数呈现不同函数关系[1].这些结果表明降雨天气条件下快速路车速变化的不确定性增加，车速准确预测的难度上升.

基于大量详实气象数据，Kyte 等[2]、Zhao等[3]、Akin等[4]使用回归技术建立了车速与气象要素的定量关系.他们发现运行车速既受大型车流量、小型车流量、密度等交通因素的显著影响，又受能见度、路面条件、降水强度、风力、天气类型、气温和地面温度等气象因素的显著影响.然而这些城市快速路车速回归模型形式和效果差异较大，决定系数R2在0.4～0.9之间不等，他们更适合于车速的离线估计而非动态预测.后来一些恶劣天气下车速预测方法研究开始涌现出来.Tsirigotis等[5]把天气信息和大车比例作为外部变量输入，对比了传统的自回归积分滑动平均模型(Autoregressive Integrated Moving Average,ARIMA)和向量自回归移动平均模型(Vector Autoregressive Moving Average,VARMA)等两类预测模型，发现在传统ARIMA模型中引入天气信息能提高预测精度，但不及采用后者模型提高效果明显.Huang等[6]则使用反馈传播神经网络模型(Back Propagation Neutral Network,BPNN)预测了速度，其输入变量多达45个，包括能见度、气温、湿度、天气类型、时段变量、当前时段实时车速等.他们的研究证实了神经网络用于恶劣天气下车速预测的可行性.Jeong等[7]利用历史数据和实时数据建立了一个三部分组成的加权移动平均预测方法，用于预测降雪条件下高速公路的速度.Thakuriah等[8]进一步比较了线性回归和支持向量机(Support Vector Machines,SVM)两种车速预测方法性能，发现融入预测天气数据和下游路段实时交通数据的支持向量机模型能有效提高实时预测精度.综合这些研究发现，神经网络和支持向量机等智能预测方法比线性系统理论方法的预测效果好.然而这两个智能方法虽具有良好的非线性逼近能力，但是缺少推理判断和知识表达能力，不容易选择合适的影响因素作为输入变量，易陷入维数灾难.另外传统的神经网络收敛速度较慢，对于实时预测应用来说也是一个缺陷.

模糊神经网络(Fuzzy Neural Networks，FNN)是模糊逻辑与神经网络相混合的综合系统，它兼具两者的优点，且物理意义明确，收敛速度快.它使用神经网络来实现模糊推理，用神经网络的权值表示模糊推理参数，并设定神经网络初值接近全局极值点，提高网络的学习性能[9].模糊神经网络根据推理过程分为前提和结论两个部分.根据结论部分差异，可分为结论是常数、线性函数和模糊变量等三种类型，其中结论为线性函数的T-S(Takagi-Sugeno)模糊神经网络具有更好的适应性[10-11].因此本文选择了主要交通流状态和气象要素指标，建立一种基于T-S模糊神经网络系统的雨天下车速预测方法.

1 降雨条件下车速预测模糊神经网络建立

1.1 基本原理

参考周忠寿[10]和何伟[11]等人的相关论述，设有n个输入变量组成的输入向量x=[x1,x2,…,xn]T，每个分量xi均为模糊语言变量，且语言变量集合为T(xi)={Ai,1,Ai,2,…,Ai,mi}i=1,2,…,n，其中Ai,si是xi的第si个语言变量值，它是定义xi在论域上的一个模糊集合，其对应的隶属度函数记为μAi,si(xi)i=1,2,…,n;si=1,2,…,mi.常用的隶属函数主要有高斯函数和钟型函数，本文使用的高斯函数如下：

(1)

式中：高斯函数中心ci和宽度δi两个参数称为前件参数.

若模型有r个输出变量组成的输出向量y=[y1,y2,…,yr]T，则T-S模型的模糊规则形式[10-11]如下(以第j系规则为例)：

如果x1是A1,s1j,…,xn是An,snj，则

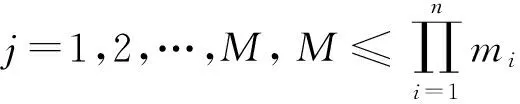
若输入量采用单点模糊集合的模糊化方法，则对于给定的输入，可利用模糊取小运算求得每条规则的适用度uj，即

(2)

则模糊系统的第k个输出量yk为每条规则的输出量ykj的加权平均，即

(3)

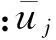
1.1.1 网络结构

为了实现基于T-S模型模糊神经网络的学习过程，一般将其转化为自适应模糊神经网络，即ANFIS(Adaptive-Network-based Fuzzy Inference Systems).假定系统为n个输入和一个输出，采用单值模糊产生器对网络进行模糊化、模糊隶属度函数采用高斯隶属函数、乘积推理规则和中心平均模糊消除器，对应的ANFIS网络结构如图1所示[12].它共有5层，前4层构成前件网络，最后1层构成后件网络.第1层计算各个输入变量的模糊隶属度；第2层计算每条规则的适用度；第3层计算适用度的归一化值；第4层计算每一条规则的输出；第5层计算所有输入数据的总输出.

1.1.2 混合学习算法

针对模糊神经网络，最常用高效的学习算法是最小二乘估计法与BP反馈算法的混合算法[11,13].他们分别用来调整系统的后件参数和前件参数，并能自动产生规则.其主要思想是首先固定前向通道中前提参数的值，利用最小二乘估计对结论参数进行优化；然后通过保持优化后结论参数恒定不变，进而利用最速梯度下降法对前提参数进行优化处理，如表1所示.

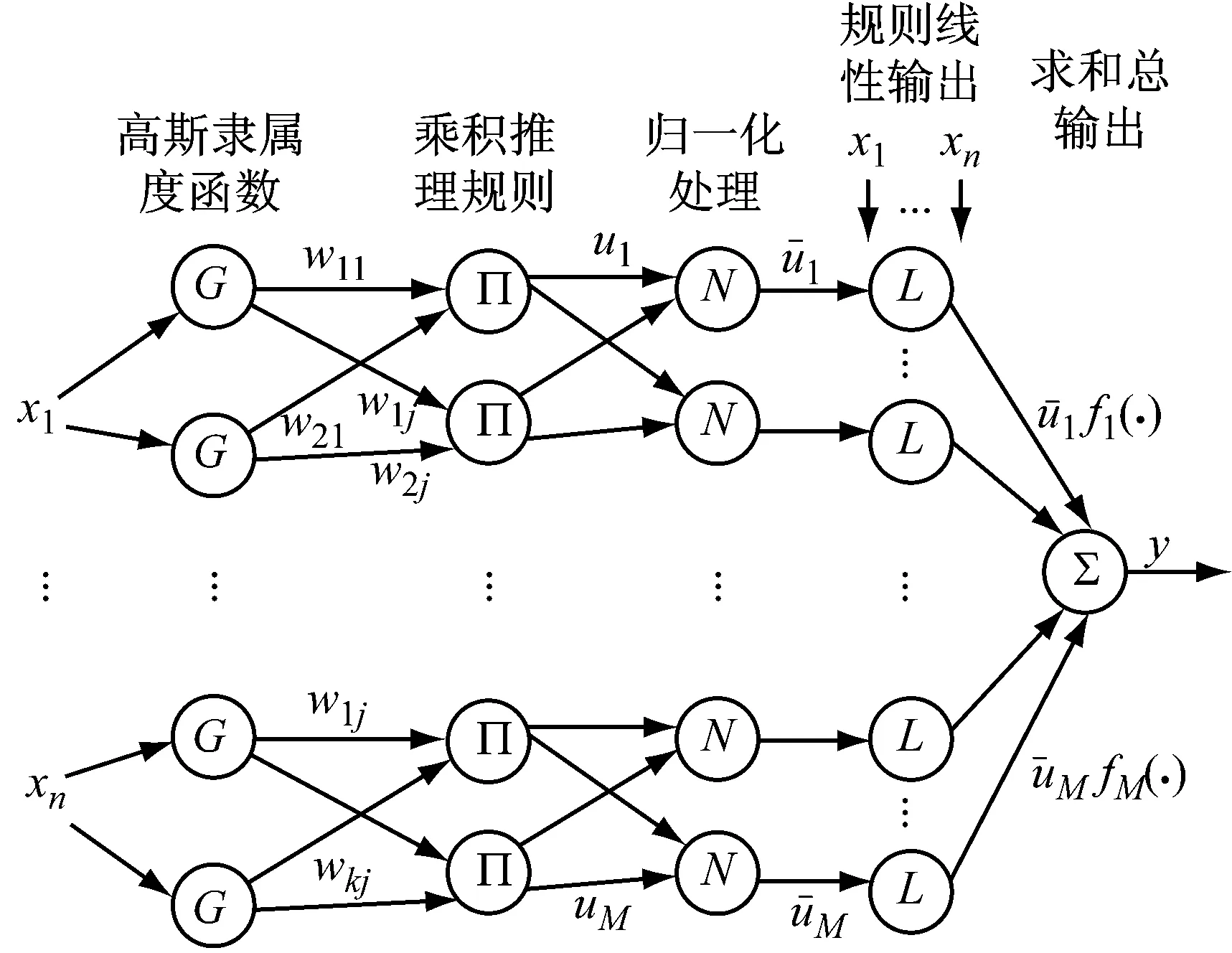
图1 多输入单输出ANFIS系统一般结构

Fig.1 General structure of ANFIS with multiple inputs single output

表1 ANFIS学习过程

1.2 自适应模糊神经网络模型建立

网络模型输入参数的选择：理论上，当交通处在拥挤状态时，车辆相互运行干扰大，此时车速主要受制于密度和流量；而当交通处于非拥挤状态时，气象的作用更为明显[14].表2为2012年8月8日东侧徐家汇上匝道至淮海中路下匝道路段(A5)的速度、流量、占有率和降雨量的相关系数.由表2可知，这3个输入参数和速度之间均存在着较高的相关性.所以选择流量、占有率和降雨量作为模型输入参数.

表2 速度、流量、占有率和降雨量的相关系数

本文建立的3输入单输出的自适应神经网络-模糊推理系统结构如图2所示.它以交通量、占有率和降雨量作为输入变量，每个变量假设有3个模糊水平，以车速作为输出变量，基于t时段的输入数据来预测t+1时段的输出值.

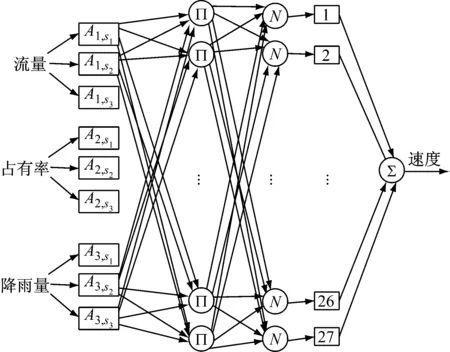
图2 雨天下车速预测的自适应神经网络模糊推理系统结构

从模糊化到输出向量共有5层，下面分别介绍各层的作用及输出：

第1层，计算各个输入变量的模糊隶属度.记ok,j为第k层第j个节点的输出，i为输入变量的模糊隶属度函数下标，流量、占有率、降雨量3个输入变量分别为x1,x2和x3，其对于不同区间的隶属度函数为μA1,si(x1)，μA2,si(x2)和μA3,si(x3)，均为高斯函数.以x1的si区间为例，其隶属度函数如下：

(4)

式中：高斯函数中心ci和宽度δi两个参数通过模糊神经网络自动调整.

这里假设流量和占有率分别有高、中、低3个区间，所以i取1～3；而降雨量也分高、中、低3个区间，因此i也取1～3.因此第1层的各节点输出结果(即隶属度)为

(5)

第2层，计算每条规则的适用度(activity intensity)，也称激励强度.该层共有27个节点，每一个节点j对应一条模糊规则，该层第j个节点的输出o2,j为所有输入o1,j相应组合的乘积.

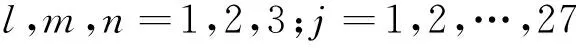
(6)

(7)

第4层，计算每一条规则的输出.若第j条规则的后件结论是yj，则第4层第j个节点的输出为

(8)

式中：ajn(j=1,2,…,27;n=0,1,2,3)为该节点的参数集, 称为后件参数.

第5层，计算有且仅有一个节点上的所有输入数据的总输出

(9)

1.3 模型参数与求解

模糊水平划分对于模糊神经网络的预测有重要影响.现有交通流状态把流量和占有率分为高、中、低3种水平；而气象行业标准把降雨量分为小雨、中雨、大雨和暴雨4种水平.考虑到变量至少有2个模糊水平，所以流量和占有率可以有2个或3个模糊水平2种划分，降雨量则有2个、3个或者4个模糊水平3种划分.因此设计了12个模糊神经网络进行比选，来确定最优的模型结构.模型命名规则为字母M与3个输入变量的模糊水平个数，比如M222表示该模型的3个输入变量均为2个模糊水平.

以模型M334为例分析网络参数.它的前件网络有(3+3+4)×2=20个参数，后件网络有(3×3×4)×(1+3)=144个参数，总计164个参数.根据前人经验，对一个神经网络而言，为了达到好的训练效果，训练的样本数要为网络参数个数的5倍，即训练样本数至少为820个.

本文利用MATLAB中anfis 函数来完成自适应模糊神经网络系统的训练和检验，包含6个步骤[12]：①输入训练数据和检验数据；②确定输入变量的隶属函数的类型和个数；③由genfis函数产生初始的Fuzzy Inference System结构；④设定Adaptive-Network-based Fuzzy Inference Systems训练的参数；⑤利用anfis 函数训练ANFIS；⑥检验得到的Adaptive-Network-based Fuzzy Inference Systems的性能.

2 算法应用

2.1 数据采集和性能指标

采用了上海市徐家汇气象自动观测站2012-08-08,2013-10-07和2013-10-08的降雨量数据，24 h降雨量分别为175.5，106.2和120.3 mm.采集了上海市南北高架上6个路段的交通流数据.研究路段和自动气象站位置如图3所示.

每个断面双环线圈检测器采集数据以每5 min为间隔汇总，每条记录包括了流量、占有率、车速等信息.提取流量、占有率、车速和降雨量数据进行匹配并统计得到交通气象数据总计为2 880条，交通流数据时间序列构成是2013年10月7日A4，A3，A1路段上全天交通流数据+2013年10月8日A4，A3，A1路段上全天交通流数据+2012年8月8日A5，A6，A2，A3路段上全天交通流数据.使用前2 592条交通气象数据训练网络模型，并使用最后的288条数据来验证模型.需要说明的是，首先需要对线圈检测的交通流数据进行异常筛选与恢复等预处理，然后再对预处理数据进行归一化处理.

本文采用3个预测性能指标.首先是均方根误差R，它表示误差数据的离散程度[15]，计算公式为

(10)

式中：N为时段数；vt为时段t实测车速；v(t)为时段t预测车速.

(11)

(12)

2.2 模型比选与结果分析

网络训练参数设置如下：输入变量的隶属函数均为高斯函数；最大训练批数为100；目标误差为0.01；初始步长为0.01；步长减少率为0.9；步长增长率为1.1；训练方法选项为混合学习算法.

2.2.1 模型比选

对12个模糊神经网络逐一训练，得到不同模糊水平数下FNN模型均方根误差如图4所示.可以看到模型M222的均方根误差R是最小的，所以是最优模型结构.因此流量、占有率、降雨量等影响因素均分为高、低2个模糊水平.下面所有结果分析均来自模型M222.

图4 不同模糊水平下FNN模型的均方根误差比较

2.2.2 训练结果分析

该模型训练误差目标值(均方根误差R的平方)从开始时的0.09很快收敛到第55步时的0.07.虽然无法达到0.01，但已具有较好的泛化能力.图5给出了网络训练输出与实际输出比较，可以看到网络实际输出能较好地跟踪训练数据变化趋势.图5中量纲一速度是指速度减去最小速度的差值与最大速度减去最小速度的差值的比值,时间间隔是指每5 min数据在时间序列中的位置序号.

图5 训练数据输出与网络实际输出比较

2.2.3 检验结果分析

对验证组车速进行预测，预测值和真实值比较如图6所示.经计算发现全天预测均方根误差R为3.05 km·h-1.早高峰(7:00—9:00)、晚高峰(17:00—19:00)、平峰(10:00—16:00和20:00—6:00)3个时段下的均方根误差分别为3.09,2.03和1.57 km·h-1.

图6 车速预测值与实测值对比

在22:00—24:00以及0:00—6:00期间预测值较平稳，而后期7:00—21:00预测震荡比较明显.这是因为夜间交通畅通，速度较高并且波动小，所以预测值也相应平稳；而白天早晚高峰交通从畅通到拥挤再恢复到畅通，速度低且波动大，因此预测值也震荡明显.另一方面降雨存在较强的时空差异性，本文仅使用单个气象站采集的小时降雨量数据，同时为了得到5 min级别的数据进行了线性插值处理，这在一定程度上也降低了预测精度.

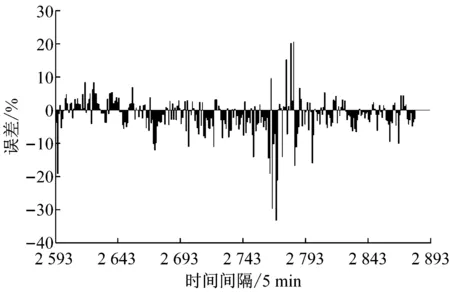
图7 误差序列

造成部分间隔误差较大的原因有：一方面模型中未考虑到不同路段交通流存在的其他影响因素，比如路段横断面、几何设计等道路条件，以及路面积水、能见度等环境条件；另一方面研究表明的天气对交通流影响的延迟效应、交通流突变现象等也没有在预测模型中有所体现.

3 相关讨论

3.1 线圈检测误差影响

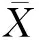
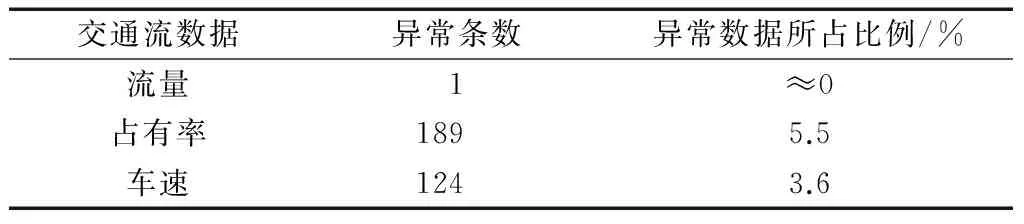
表3 交通流异常数据统计

3.2 与现有方法预测性能比较

为了说明本文模糊神经网络方法(FNN)的优越性，研究也分别实现了基于自回归求和滑动平均(ARIMA)的、基于BP神经网络(BPNN)的和基于支持向量机(SVM)的3种常用交通流预测方法[5-8].ARIMA有自回归阶数(p)、差分次数(d)和移动平均阶数(q)等3个参数.观察时间数据序列的自相关和偏相关函数图，确定数据序列模型参数.BPNN是具有同样3个影响因素的输入层，7个神经元的中间隐层和1个车速输出层的3层网络结构.其中修正权值的学习速率为0.05，最大循环次数为100，期望误差最小值为0.001.SVM 输入也是同样3个影响因素.根据经验和实验，核函数选用Gauss RBF函数，核参数σ=0.33，惩罚因子C=0.8.

图8 不同预测方法性能比较

4 结论

为了提高雨天条件下快速路车速的短时预测精度，研究了基于模糊神经神经网络的雨天条件下快速路车速短期预测方法.首先选择了流量、占有率、降雨量作为影响雨天下车速的主要因素，建立了一个3输入单输出的自适应模糊神经网络模型.然后借助MATLAB工具箱利用上海市快速路交通流和气象数据进行训练，使用均方根误差、平均误差等指标检验了模型预测效果.最后讨论了线圈检测误差的影响以及对比分析了与现有3种常用方法预测效果.本文得到以下两点结论：

(1)流量、占有率、降雨量等影响因素均分为高、低2个模糊水平比较合适.

(2)利用模糊神经网络来预测车速是可行的，且预测精度要高于自回归积分滑动平均模型、反向传播神经网络模型和支持向量机模型的预测效果.

[1] 施莉娟.不良天气对快速路交通运行影响研究[D].上海：同济大学，2012.

SHI Lijuan. The effects of adverse weathers on urban freeway traffic flow[D]. Shanghai: Tongji University, 2012.

[2] Kyte M, Khatib Z. Effect of environmental factors on free-flow speed[J]. Transportation Research Circular, 2000, 56(2):181.

[3] Zhao Y, Sadek A W, Fuglewicz D. Modeling the impact of inclement weather on freeway traffic speed at macroscopic and microscopic levels[J]. Transportation Research Record: Journal of the Transportation Research Board, 2012, 2272(1): 173.

[4] Akin D, Sisiopiku V P, Skabardonis A. Impacts of weather on traffic flow characteristics of urban freeways in Istanbul[J]. Procedia-Social and Behavioral Sciences, 2011, 16(1): 89.

[5] Tsirigotis L, Vlahogianni E I, Karlaftis M G. Does information on weather affect the performance of short-term traffic forecasting models?[J]. International Journal of Intelligent Transportation Systems Research, 2012, 10(1):1.

[6] Huang S, Ran B. An application of neural network on traffic speed prediction under adverse weather condition[C/CD]//Submitted to Transportation Research Board 2003 Annual Meeting. Washington D C: Transportation Research Board, 2003:00944270.

[7] Jeong E, Oh C, Kim Y,etal. A framework to predict freeway traffic speed in snowy weather: integration of historical and real-time patterns[C/CD]// Transportation Research Board 93rd Annual Meeting. Washington D C: Transportation Research Board, 2014: 0517559.

[8] Thakuriah P V, Tilahun N. Incorporating weather information into real-time speed estimates: comparison of alternative models [J]. Journal of Transportation Engineering, 2012,39(4): 379.

[9] 张化光，何希勤.模糊自适应控制理论及应用[M].北京：北京航空航天大学出版社,2002.

ZHANG Huaguang, HE Xiqin. Fuzzy adaptive control: theory and application [M].Beijing: Beijing University of Aeronautics and Astronautics Press, 2002.

[10] 周忠寿. 基于T-S模型的模糊神经网络在水质评价中的应用[D].南京：河海大学,2007.

ZHOU Zhongshou. The application of fuzzy neural network based on T-S model in water quality evaluation[D].Nanjing: Hohai University,2007.

[11] 何伟. 模糊神经网络在交通流量预测中的应用研究[D].兰州：兰州交通大学,2012.

HE Wei. Research on prediction of traffic flow using fuzzy neural networks [D].Lanzhou: Lanzhou Jiaotong University,2012.

[12] 曾庆茂. 基于神经网络和模糊推理的信息融合技术[D].西安：西安科技大学,2005.

ZENG Qingmao. Information fusion technique based on neural network and fuzzy inference[D].Xi’an: Xi’an University of Science and Technology, 2005.

[13] 王雅琳. 智能集成建模理论及其在有色冶炼过程优化控制中的应用研究[D].长沙：中南大学,2001.

WANG Yalin. Study on intelligent integrated modeling theory and its applications to optimal control of nonferrous metallurgical process[D]. Changsha: Central South University, 2001.

[14] 肖琳. 特殊需求下网络交通拥挤传播机理及态势评估[D].上海：同济大学，2013.

XIAO Lin. Propagation mechanisms and trends assessment of traffic congestion under special conditions[D]. Shanghai: Tongji University, 2013.

[15] Zhang Y, Ge H. Freeway travel time prediction using takagi-sugeno-kang fuzzy neural network[J]. Computer-Aided Civil and Infrastructure Engineering, 2013,28(8):594.

[16] 吴兴华,周晖. 基于减法聚类及自适应模糊神经网络的短期电价预测[J]. 电网技术,2007,19(31):69.

WU Xinghua, ZHOU Hui. Short-term electricity price forecasting based on subtractive clustering and adaptive neuro-fuzzy inference system[J]. Power System Technology, 2007, 19(31):69.

Fuzzy Neural Network System for Urban Expressway Speed Prediction on Rainy Days

SUN Hongyun1, YANG Jinshun2, LI Linbo1, WU Bing1

(1.Key Laboratory of Road and Traffic Engineering of the Ministry of Education, Tongji University, Shanghai 201804, China; 2.School of Automobile and Transportation, Qingdao University of Technology, Qingdao 266555, China)

A fuzzy neural network system was developed to improve urban expressway short-term speed prediction accuracy on rainy days, taking fuzzy influencing factors such as traffic volume, occupancy and precipitation, as well as their non-linear interaction into account. Based on the traffic flow and weather data of Shanghai, the best model structure was determined and its performance was evaluated against those of the existing autoregressive integrated moving average model, the back propagation neutral network, and the support vector machines model. The results show that the root mean square error and mean absolute percent error of the fuzzy neural network system are 3.05 km·h-1and 3.95% respectively, which outperform those of the other three prediction models.

urban expressway; speed prediction; fuzzy neural network; traffic state; rainfall

2015-10-06

孙洪运(1985—)，男，博士生，主要研究方向为交通运输规划与管理.E-mail：shy1985tj@163.com

吴 兵(1960—)，男，教授，博士生导师，工学博士，主要研究方向为交通运输规划与管理.E-mail:wubing@tongji.edu.cn

U491.2

A