REGULAR SPACE-LIKE HYPERSURFACES IN THE DE SITTER SPACEWITH PARALLEL BLASCHKE TENSORS

LI Xing-xiao,SONG Hong-ru

(School of Mathematics and Science Information,Henan Normal University,Xinxiang 453007,China)

REGULAR SPACE-LIKE HYPERSURFACES IN THE DE SITTER SPACEWITH PARALLEL BLASCHKE TENSORS

LI Xing-xiao,SONG Hong-ru

(School of Mathematics and Science Information,Henan Normal University,Xinxiang 453007,China)

In this paper,we introduce two conformal non-homogeneous coordinate systems. Modeled on the de Sitter space,we cover the conformal space.The conformal geometry of regular space-like hypersurfaces incan be treated as in the Mbius geometry of hypersurfaces in the sphere Sm+1.As a result,we give a complete classification of the regular space-like hypersurfaces with parallel Blaschke tensors.

conformal form;parallel Blaschke tensor;conformal metric;conformal second fundamental form;maximal hypersurfaces;constant scalar curvature

2010 MR Subject Classification:53A30;53B25

Document code:AArticle ID:0255-7797(2016)06-1183-18

1　Introduction

where the dot“·”is the standard Euclidean inner product either on Rsor on Rm.

Denote by RPm+2the real projection space of dimension m+2.Then the so called conformal spaceis defined as(see[1])

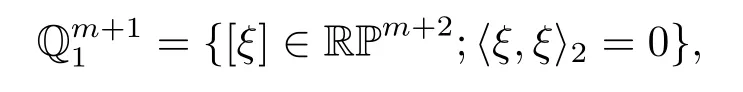
while,for any a＞0,the de Sitter space(a)and the anti-de Sitter spaceare defined respectively by

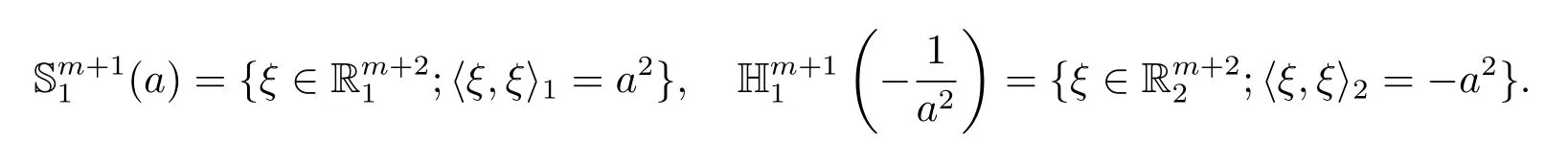
Then there are three conformal diffeomorphisms from the Lorentzian space forms into the conformal space

In the reference[1],Nie at al.successfully set up a unified framework of conformal geometry for both regular surfaces and hypersurfaces in Lorentzian space forms by introducing the conformal spaceand some basic conformal invariants,including the conformal metric g,the conformal form Φ,the Blaschke tensor A and the conformal second fundamental form B.Later,all of these were generalized to regular submanifolds of higher codimensions(see [2]).Under this framework,several characterization or classification theorems were obtained for hypersurfaces with some special conformal invariants,see for example(see[1,3]).The achievement of these certainly proves the efficiency of the above framework.In particular,as the main theorems,regular hypersurfaces with parallel conformal second fundamental forms, and conformal isotropic submanifolds were classified in[1]and[2],respectively.Note that, a regular submanifold in the conformal spacewith vanishing conformal form is called conformal isotropic if its Blaschke tensor A is parallel to the conformal metric.For the later use,we rewrite these two theorems applied in the special case of space-like hypersurfaces as follows.

Theorem 1.1[1]Let x:Mm→be a regular space-like hypersurface with parallel conformal second fundamental form.Then x is locally conformal equivalent to one of the following hypersurfaces

Theorem 1.2[2]Any regular,space-like and conformal isotropic hypersurface inis conformal equivalent to a maximal,space-like and regular hypersurface inorwith constant scalar curvature.

Motivated by the above theorems,we aims in the present paper at a complete classification of regular space-like hypersurfaces inwith parallel Blaschke tensors.To this end, we would like to make a direct use of the ideas and technics with which we previously studied the Mbius geometry of umbilc-free hypersurfaces in the unit sphere(see[6-9]).So we firstly define two conformal non-homogeneous coordinate systems(with the coordinate mapsrespectively)covering the conformal space,which are modeled on the de Sitter space,so that the conformal geometry of the hypersurfaces incorresponds right to that of the hypersurfaces in the de Sitter space.It follows that the conformal geometry of regular hypersurfaces in each ofandis made unified with that in.This shows that we only need to consider and study the conformal invariants of the hypersurfaces inwhich plays the same role as the unit sphere does in the Mbius geometry of umbilic-free submanifolds.With this consideration,we only focus here on the study of the conformal invariants of regular space-like hypersurfaces in the de Sitter space.As a result,we are able to establish a complete classification for all the regular space-like hypersurfaces with parallel Blaschke tensors.

Note that the above two conformal non-homogeneous coordinate mapsandare conformal equivalent where both of them are defined.Therefore we can use Ψ to denote either one ofand.By this,the main theorem of the present paper is stated as follows.

Theorem 1.3 Let x:Mm→,m≥2,be a regular space-like hypersurface.If the Blaschke tensor A of x is parallel,then one of the following holds.

1.x is conformal isotropic and thus is locally conformal equivalent to a maximal spacelike regular hypersurface inwith constant scalar curvature,or the conformal image under Ψ◦σ-1of a maximal regular hypersurface inwith constant scalar curvature,or the conformal image under Ψ◦σ0of a maximal regular hypersurface inwith constant scalar curvature;

2.x is of parallel conformal second fundamental form B and thus is locally conformal equivalent to

(c)the image under Ψ◦σ-1of Hk0＜a＜1,k= 1,···m-1;or

3.x is non-isotropic with a non-parallel conformal second fundamental form B and is locally conformal equivalent to

(a)one of the maximal hypersurfaces as indicated in Example 3.2;or

(b)one of the non-maximal hypersurfaces as indicated in Example 3.3.

Remark 1.1 It is directly verified in Section 3 that each of the regular space-like hypersurfaces stated in the above theorem has a parallel Blaschke tensor.

2　Necessary Basics on Regular Space-Like Hypersurfaces

This section provides some basics of the conformal geometry of regular space-like hypersurfaces in the Lorentzian space forms.The main idea comes originally from the work of Wang on the Mbius geometry of umbilic-free submanifolds in the unit sphere(see[10]), and much of the detail can be found in a series of papers by Nie at al(see for example[1-3]).

Let x:Mm→be a regular space-like hypersurface in.Denote by h the(scalar-valued)second fundamental form of x with components hijand H=the mean curvature.Define the conformal factor ρ＞0 and the conformal position Y of x, respectively,as follows

Then Y(Mm)is clearly included in the light cone Cm+2⊂,where

The positivity of ρ implies that Y:Mm→is an immersion of Mminto theClearly,the metric g:=〈dY,dY〉2≡ρ2〈dx,dx〉1on Mm,induced by Y and called the conformal metric,is invariant under the pseudo-orthogonal group O(m+3,2)of linear transformations onreserving the Lorentzian product〈·,·〉2.Such kind of things are called the conformal invariants of x.

Definition 2.1(see[1-3])Let x,:Mm→be two regular space-like hypersurfaces with Y,their conformal positions,respectively.If there exists some T∈O(m+3,2) such that=T(Y),then x,are called conformal equivalent to each other.

For any local orthonormal frame field{ei}and the dual{θi}on Mmwith respect to the standard metric〈dx,dx〉1,define

Then{Ei}is a local orthonormal frame field with respect to the conformal metric g with {ωi}its dual coframe.Let n be the time-like unit normal of x.Define ξ=(-H,-Hx+n), then〈ξ,ξ〉2=-1.Let∆denote the Laplacian with respect to the conformal metric g. Define N:Mm→by

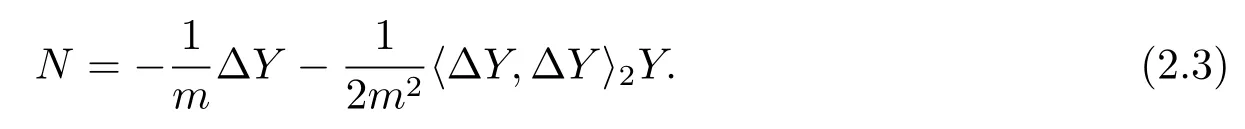
Then it holds that

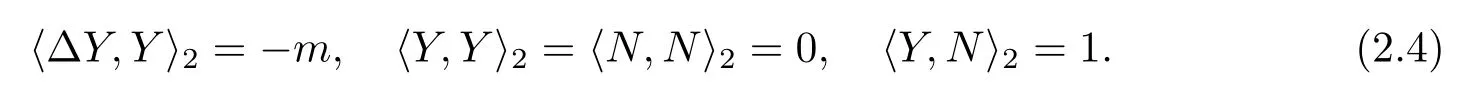
Furthermore,{Y,N,Yi,ξ,1≤i≤m}forms a moving frame inalong Y,with respectto which the equations of motion is as follows

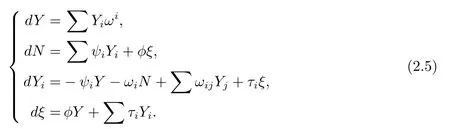
By the exterior differentiation of(2.5)and using Cartan's lemma,we can write

Then the conformal form Φ,the Blaschke tensor A and the conformal second fundamental form B defined by

are all conformal invariants.By a long but direct computation,we find that

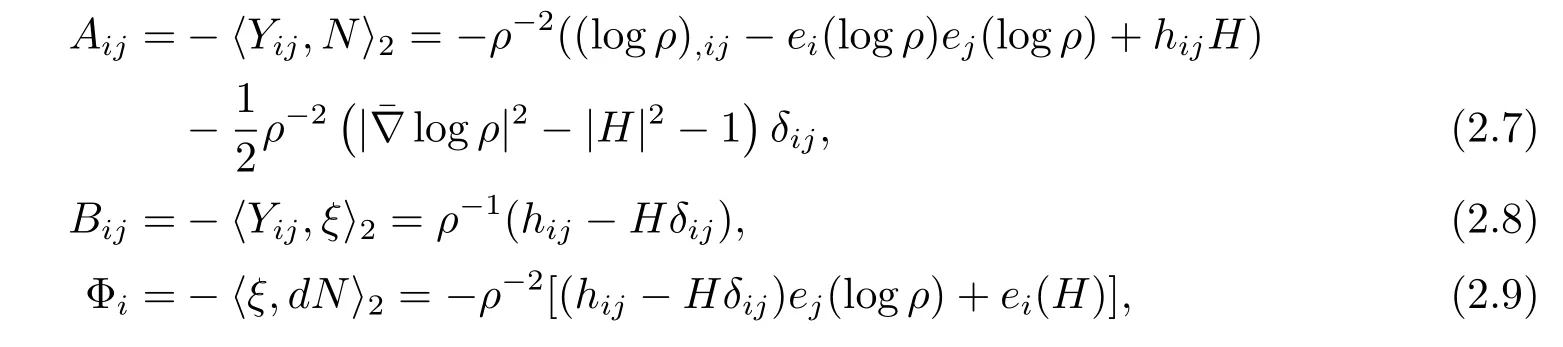
where Yij=Ej(Yi),is the Levi-Civita connection of the standard metric〈·,·〉1,and the subscript,ijdenotes the covariant derivatives with respect to.The differentiation of(2.5) also gives the following integrability conditions

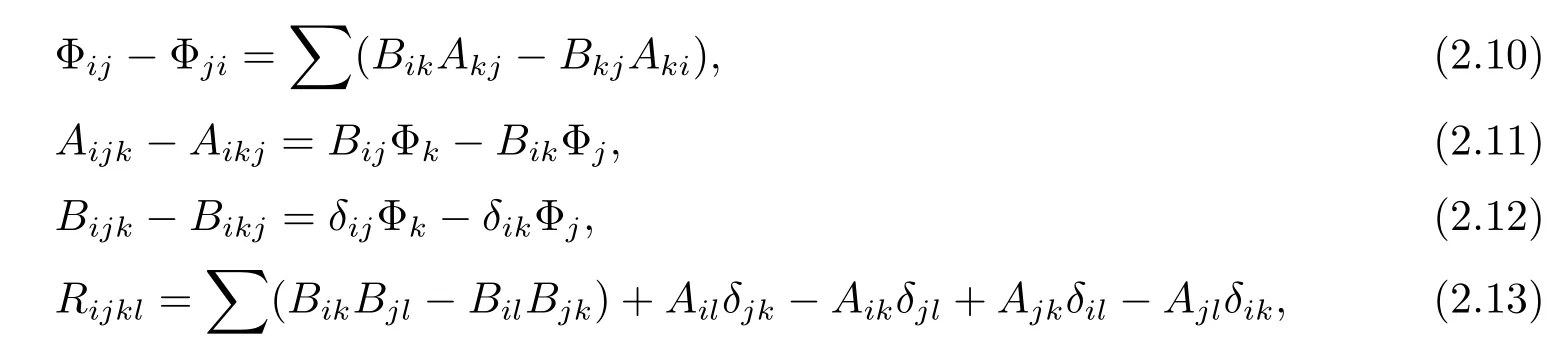
where Aijk,Bijk,Φijare respectively the components of the covariant derivatives of A,B, Φ,and Rijklis the components of the Riemannian curvature tensor of the conformal metric g.Furthermore,by(2.1)and(2.8)we have

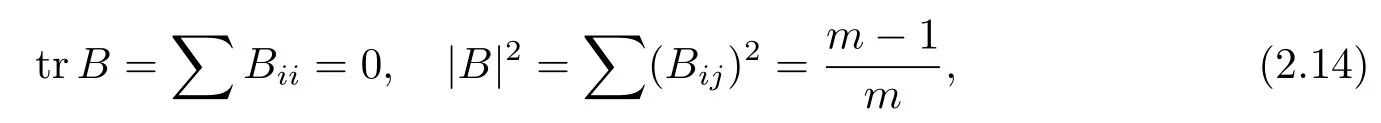
and by(2.13)we find the Ricci curvature tensor

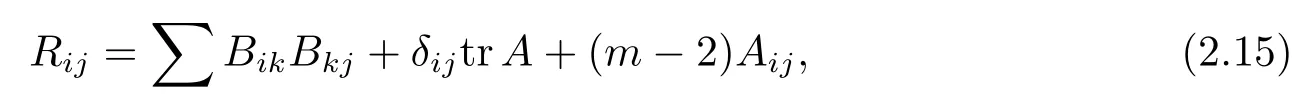
which implies that

with κ being the normalized scalar curvature of g.

It is easily seen[1]that the conformal position vector Y defined above is exactly the canonical lift of the composition map=σ1◦x:Mm→,implying that the conformal invariants g,Φ,A,B defined above are the same as those ofintroduced by Nie at al.in[1].

On the other hand,the conformal spaceis clearly covered by the following two open sets

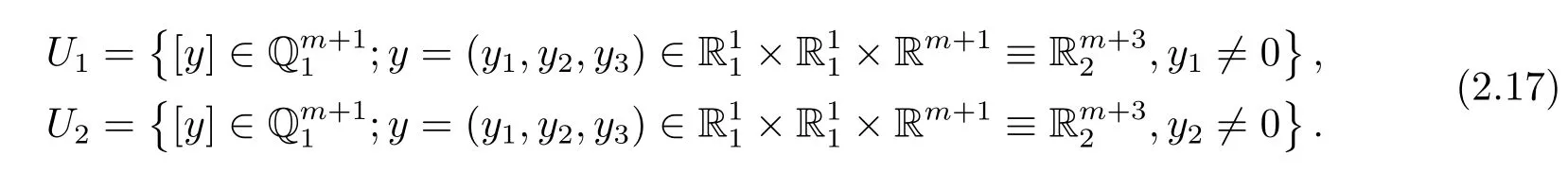
Define the following two diffeomorphisms

by

Then with respect to the conformal structure onintroduced in[1]and the standard metric on,bothandare conformal.

Now for a regular space-like hypersurfacewith the canonical lift

write Y=(Y1,Y2,Y3)∈×Rm+1.Then we have the following two composed hypersurfaces

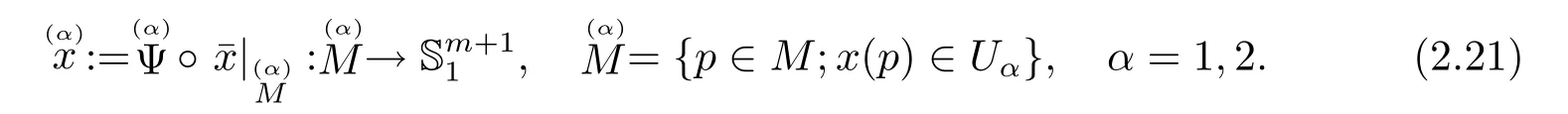
Then Mm=and the following lemma is clearly true by a direct computation:

Lemma 2.1 The conformal position vectoris nothing butwhile the conformal position vectoris given by

Corollary 2.2 The basic conformal invariants g,Φ,A,B ofcoincide accordingly with those of each ofon whereis defined,respectively.

On the other hand,all the regular space-like hypersurfaces in the three Lorentzian space forms can be viewed as ones invia the conformal embeddings σ1,σ0and σ-1defined in(1.1).Now,usingone can shift the conformal geometry of regular space-like hypersurfaces into that of regular space-like hypersurfaces in the de Sitter spaceIt follows that,in a sense,the conformal geometry of regular space-like hypersurfaces can also be unified as that of the corresponding hypersurfaces in the de Sitter space.Concisely, we can achieve this simply by introducing the following four conformal maps

where

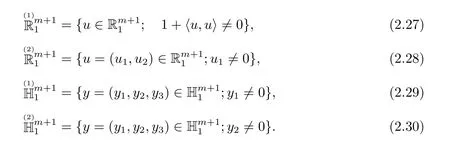
The following theorem will be used later in this paper.

Theorem 2.4[2]Two hypersurfaces x:Mm→(m≥3) are conformal equivalent if and only if there exists a diffeomorphism f:M→which preserves the conformal metric and the conformal second fundamental form.

3　Examples

Before proving the main theorem,we first present some regular space-like hypersurfaces inwith parallel Blaschke tensors.

Example 3.1(see[1,4])Let R+be the half line of positive real numbers.For any two given natural numbers p,q with p+q＜m and a real number a＞1,consider the hypersurface of warped product embedding

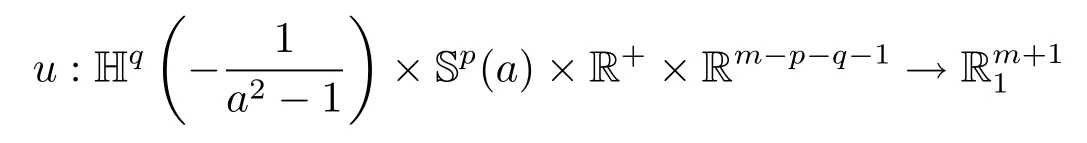
defined by

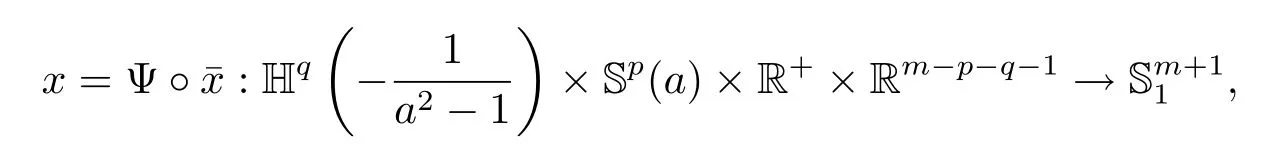
The similar example of WP(p,q,a)in Mbius geometry was originally found by[4]and denoted by CSS(p,q,a).

Example 3.2 Given r＞0.For any integers m and K satisfying m≥3 and 2≤K≤ m-1,letbe a regular and maximal space-like hypersurface with constant scalar curvature

and

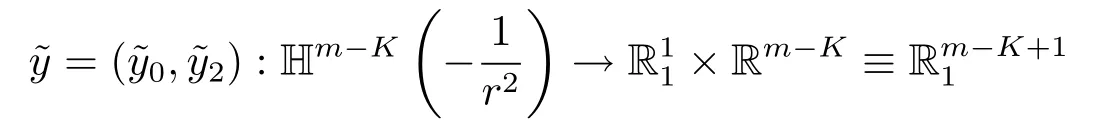
be the canonical embedding,where0＞0.Set

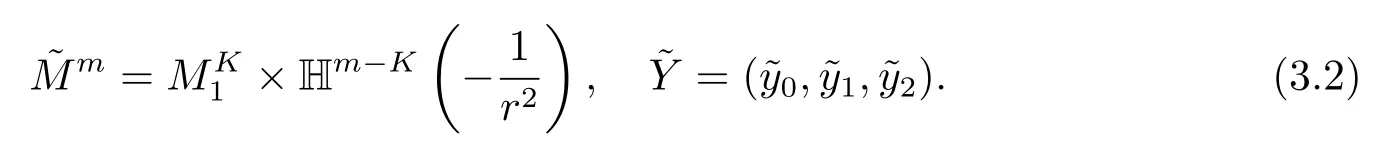
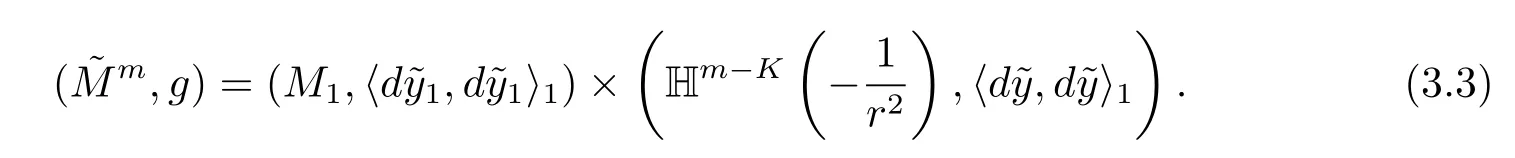
Define

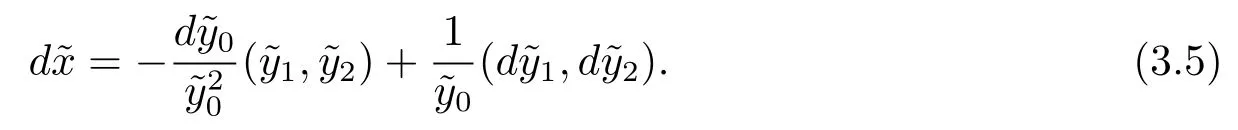
Therefore the induced“metric”=d·dis derived as

where h is the second fundamental form of

Let{Ei;1≤i≤K}(resp.{Ei;K+1≤i≤m})be a local orthonormal frame field onThen{Ei;1≤i≤m}gives a local orthonormal frame field oni=1,···,m.Then{ei;1≤i≤m}is a orthonormal frame field along.Thus we obtain

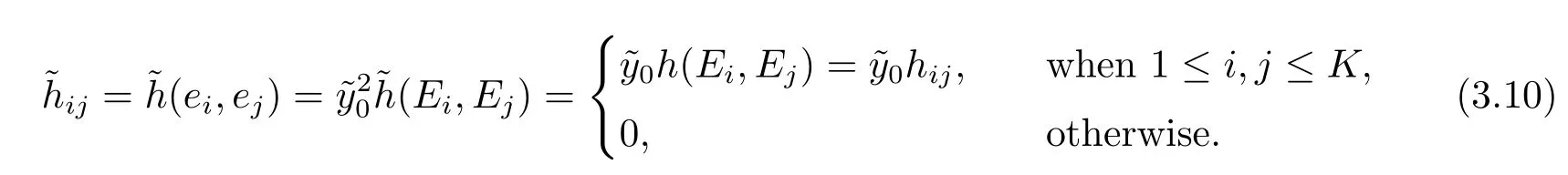
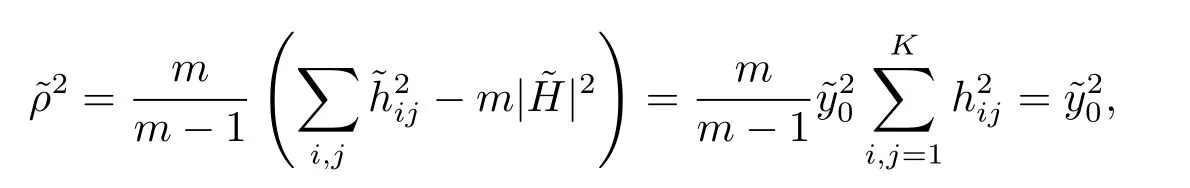
where we have used the Gauss equation and(3.1).It follows thatis regular and its conformal factor=0.Thus,given in(3.2),is exactly the conformal position vector of,implying the induced metric g byis nothing but the conformal metric of.Furthermore, the conformal second fundamental form ofis given by

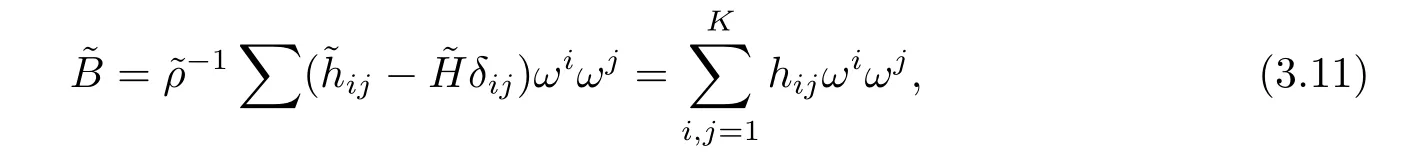
where{ωi}is the local coframe field on Mmdual to{Ei}.

On the other hand,by(3.3)and the Gauss equations of1and,one finds that the Ricci tensor of g is given as follows

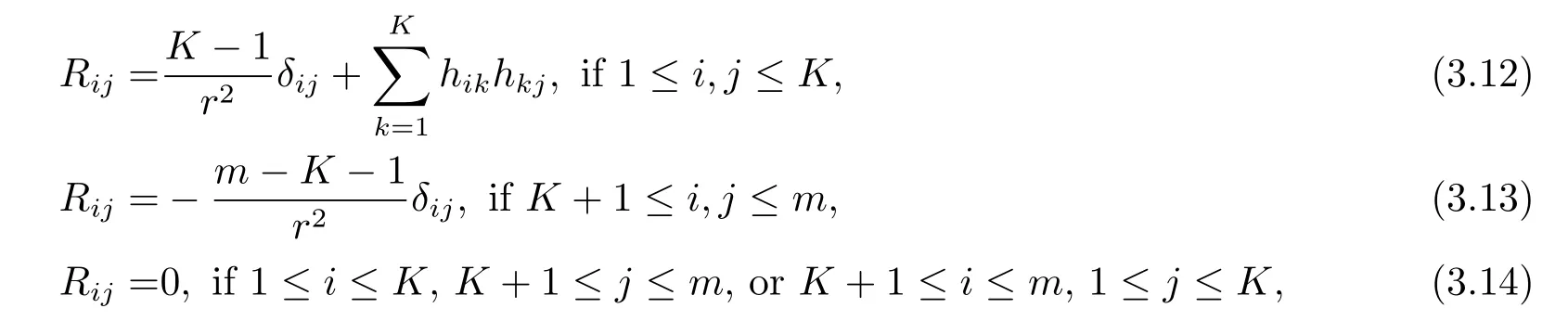
which implies that the normalized scalar curvature of g is given by

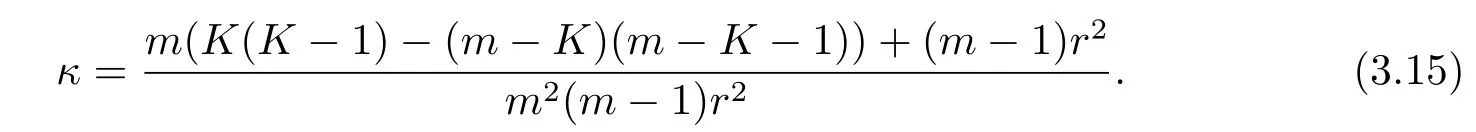
Thus

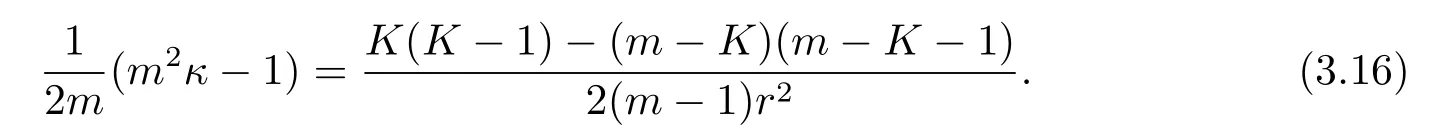
Since m≥3,it follows from(2.15)and(3.11)-(3.16)that the Blaschke tensor ofis given by A=∑Aijωiωj,where

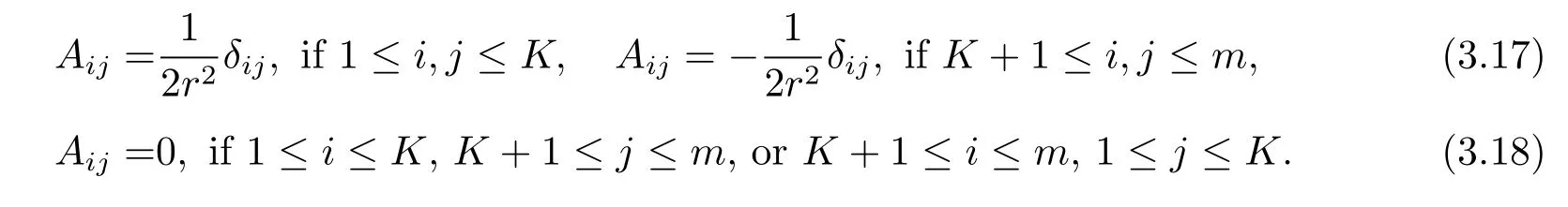
Clearly,A has two distinct eigenvalues,which are constant.Thus by (3.3),A is parallel.

Example 3.3 Given r＞0.For any integers m and K satisfying m≥3 and 2≤K≤m-1,let

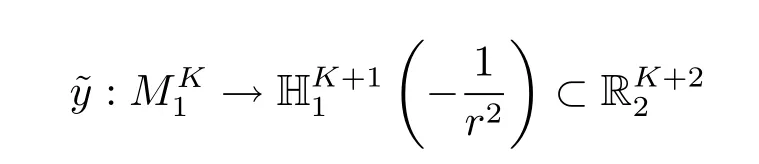
be a regular and maximal space-like hypersurface with constant scalar curvature

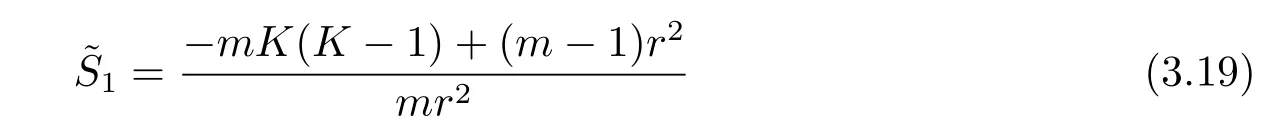
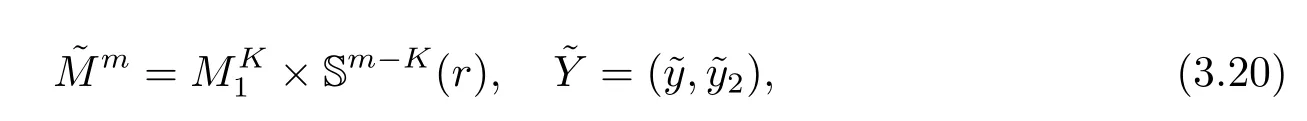
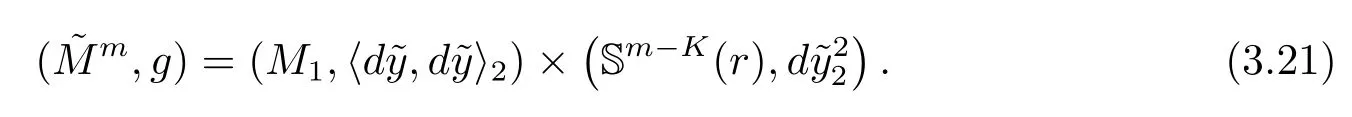
Suitably choose the time-like unit normal vector field(0,1)of,define

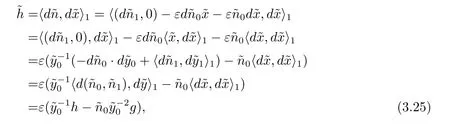
where h is the second fundamental form of.

Let{Ei;1≤i≤K}(resp.{Ei;K+1≤i≤m})be a local orthonormal frame field on (M1,d2)(resp.on Sm-K(r)).Then{Ei;1≤i≤m}is a local orthonormal frame field on (Mm,g).Put ei=ε0Ei,i=1,···,m.Then{ei;1≤i≤m}is a local orthonormal frame field with respect to the metric=〈d,d〉1.Thus

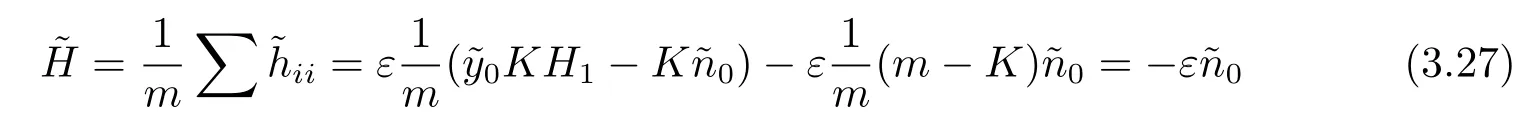
and

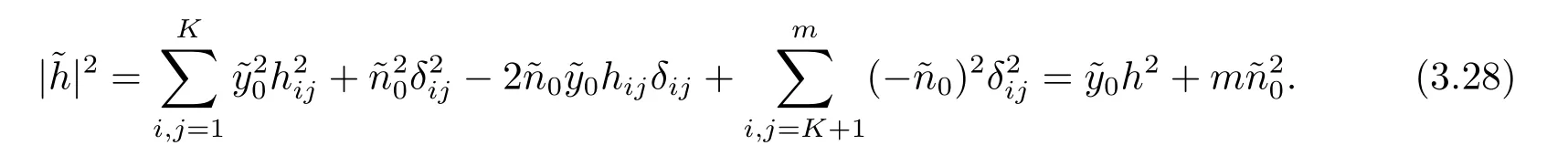
Therefore,by definition,the conformal factorofis determined by

where we have used the Gauss equation and(3.19).Hence=|0|=ε0＞0 and thus=(1,)is the conformal position vector of.Consequently,the conformal metric ofis defined by〈d,d〉2=g.Furthermore,the conformal second fundamental form ofis given by

where{ωi}is the local coframe field on Mmdual to{Ei}.

On the other hand,by(3.21)and the Gauss equations of1and,one finds the Ricci tensor of g as follows

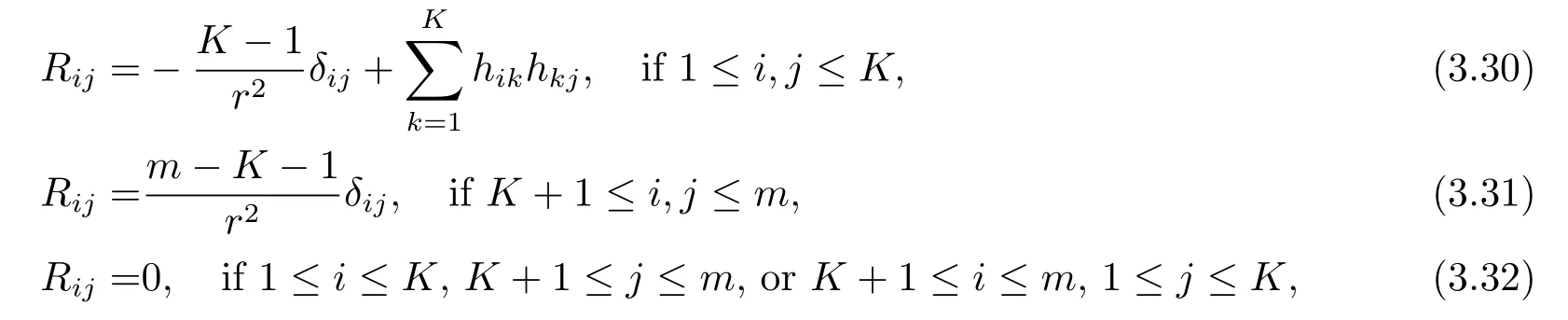
which implies that the normalized scalar curvature of g is given by

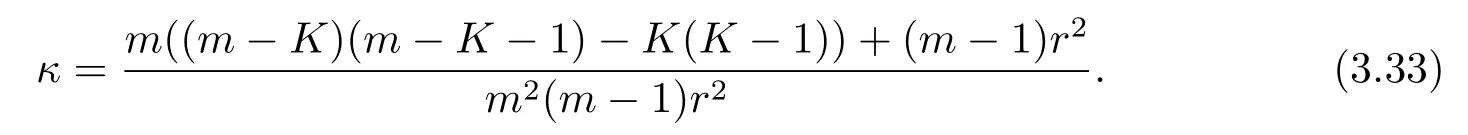
Thus

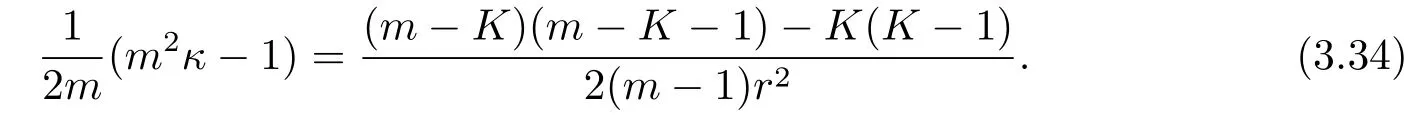
Since m≥3,it follows from(2.15)and(3.29)-(3.34)that the Blaschke tensor ofis given by A=∑Aijωiωj,where

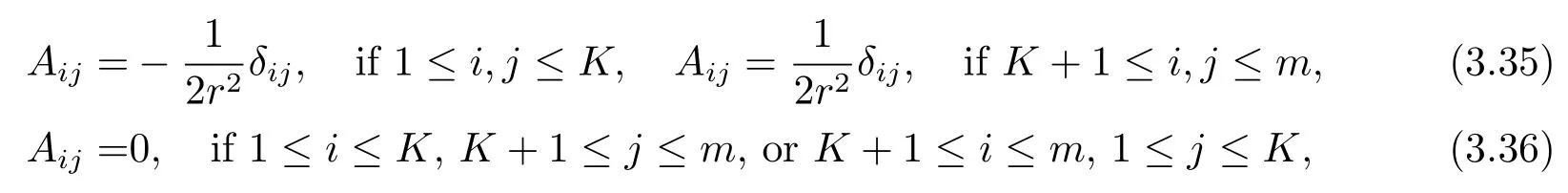
which,once again,implies that A is parallel with two distinct eigenvalues λ1=-λ2=

4　Proof of Main Theorem

To make the argument more readable,we divide the proof into several lemmas.

Let x:Mm→be a regular space-like hypersurface.

Lemma 4.1 If the Blaschke tensor A is parallel,then the conformal form Φ vanishes identically.

Proof For any given point p∈Mm,take an orthonormal frame field{Ei}around p with respect to the conformal metric g,such that Bij(p)=Biδij.Then it follows from(2.11) that

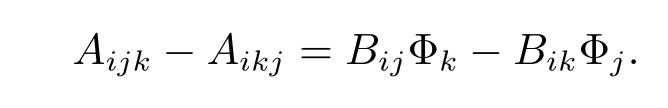
Since A is parallel,Aijk=0 for any i,j,k.Thus at the given point p,we have

By(2.14),there are different indices i1,i2such that Bi10 and Bi20.Then for any indices i,j,we have

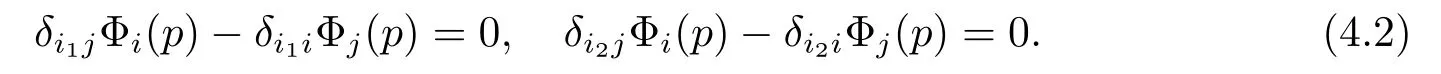
If i=i1,put j=i2;if ii1,put j=i1.Then it follows from(4.2)that Φi(p)=0.By the arbitrariness of i and p,we obtain that Φ≡0.

Remark 4.1Since A is parallel,then all eigenvalues of the Blaschke tensor A of x are constant on Mm.From the equation

we obtain that

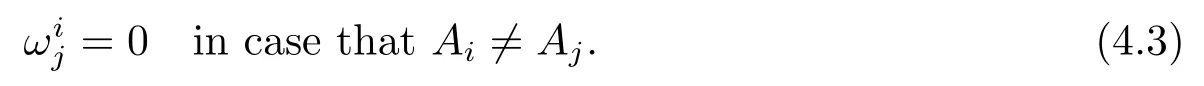
Lemma 4.2 If A is parallel,then Bij=0 as long as AiAj.

Proof Since A is parallel,there exists around each point a local orthonormal frame field{Ei}such that

It follows from(2.10)and Lemma 4.1 that=0.Then we have Bij(Aj-Ai)=0.

Now,let t be the number of the distinct eigenvalues of A,and λ1,···,λtdenote the distinct eigenvalues of A.Fix a suitably chosen orthonormal frame field{Ei}for which the matrix(Aij)can be written as

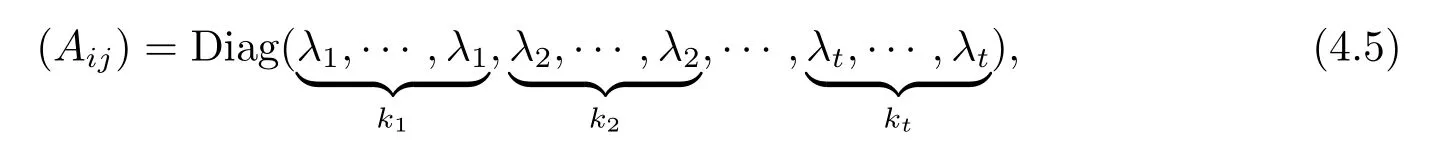
or equivalently,

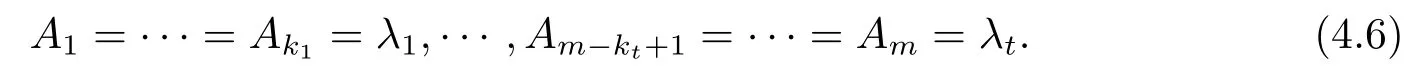
Lemma 4.3 Suppose that t≥3.If,with respect to an orthonormal frame field{Ei}, (4.5)holds and at a point p,Bij=Biδij,then Bi=Bjin the case that Ai=Aj.

Proof By(4.3),for any i,j satisfying AiAj,we have=0.Differentiating this equation,we obtain from(2.13)that 0=Rijji=B2ij-BiiBjj+Aii-Aijδij+Ajj-Aijδij. Thus at p,it holds that

If there exist indices i,j such that Ai=Ajbut BiBj,then for all k satisfying AkAi,we have

It follows from(4.8)that(Bi-Bj)Bk=0,which implies that Bk=0.Thus by(4.8),we obtain Ak=-Ai=-Aj.This implies that t=2,contradicting the assumption.

Corollary 4.4 If t≥3,then there exists an orthonormal frame field{Ei}such that

Furthermore,if(4.5)holds,then

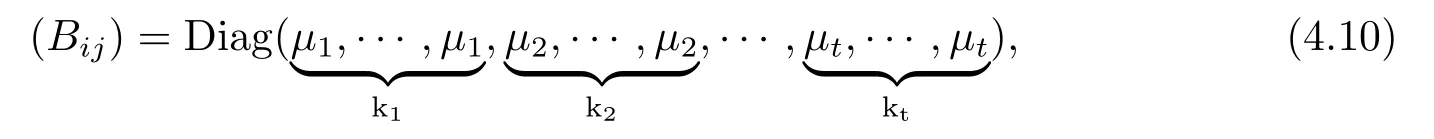
that is

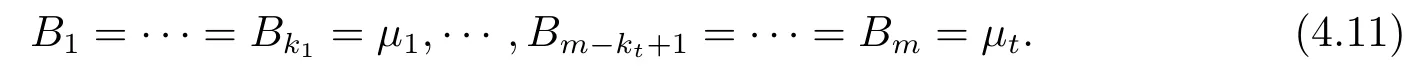
Proof Since A is parallel,we can find a local orthonormal frame field{Ei},such that (4.5)holds.It then suffices to show that,at any point,the component matrix(Bij)of B with respect to{Ei}is diagonal.Note that k1,...,ktare the multiplicities of the eigenvalues λ1,···,λt,respectively.By Lemma 4.2,we can write(Bij)=Diag(B(1),···,B(t)),where B(1),···,B(t)are square matrices of orders k1,···,kt,respectively.For any point p,we can choose a suitable orthogonal matrix T of the form T=Diag(T(1),···,T(t)),with T(1),···,T(t)being orthogonal matrices of orders k1,···,kt,such that

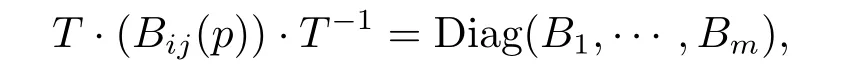
where B1,···,Bmare the eigenvalues of tensor B at p.It then follows from Lemma 4.3 that B1=···=Bk1:=µ1,···,Bm-kt+1=···=Bm:=µt.Hence

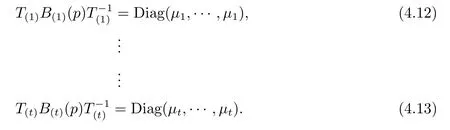
Therefore

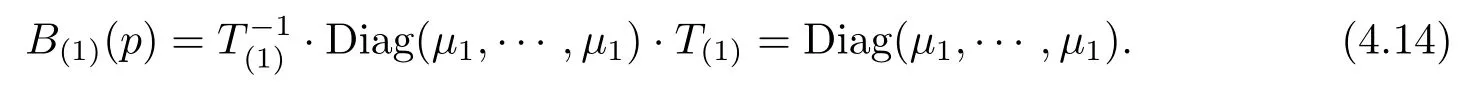
In the same way,

Thus

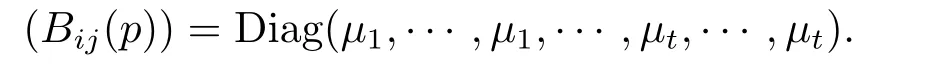
Lemma 4.5 If t≥3,then all the conformal principal curvaturesµ1,···,µtof x are constant,and hence x is conformal isoparametric.

Proof Without loss of generality,we only need to show thatµ1is constant.To this end,choose a frame field{Ei}such that(4.5)and(4.10)hold.Note that,by(4.3),when 1≤i≤k1and j＞k1,we have

which implies that Bijk=0.

By Lemma 4.1,Φ≡0.Hence from(2.12)one seen that Bijkis symmetric with respect to i,j,k.It follows that Bijk=0,in case that two indices in i,j,k are less than or equal to k1with the other index larger than k1,or one index in i,j,k is less than or equal to k1with the other two indices larger than k1.In particular,for any i,j satisfying 1≤i,j≤k1,

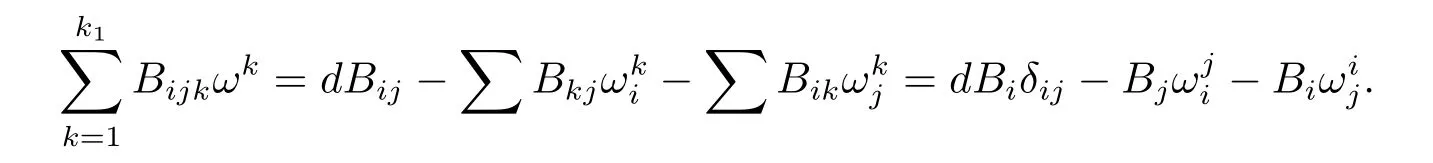
Putting j=i,one obtains

which implies that

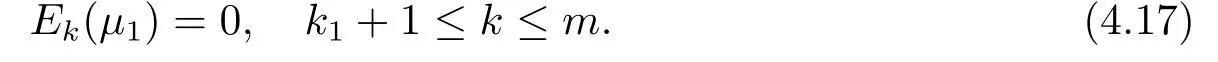
Similarly,

On the other hand,we see from(4.7)that

hold identically.Differentiating(4.19)in the direction of Ek,1≤k≤k1,and using(4.18), we obtain

By(2.14)there exists some index j such that k1+1≤j≤m and Bj0.Therefore, Ek(µ1)=0 for 1≤k≤k1.This together with(4.17)implies thatµ1is a constant.

Corollary 4.6If t≥3,then t=3 and B is parallel.

Proof Indeed,the conclusion that B is parallel comes from(4.3),Corollary 4.4 and Lemma 4.5.

If t＞3,then there exist at least four indices i1,i2,i3,i4,such that Ai1,Ai2,Ai3,Ai4are distinct each other.Then it follows from(4.7)that

Consequently,we obtain(Ai1-Ai4)(Ai2-Ai3)=0,a contradiction.

Lemma 4.7If t≤2 and B is not parallel,then one of the following cases holds:

(1)t=1 and x is conformal isotropic;

(2)t=2,λ1+λ2=0 and Bi=0 either for all 1≤i≤k1,or for all k1+1≤i≤m.

Proof Note that Φ≡0.Thus x is conformal isotropic if and only if t=1.

If t=2,then for any point p∈Mm,we can find an orthonormal frame field{Ei}such that(4.9)holds at p.

By(4.3),we see that

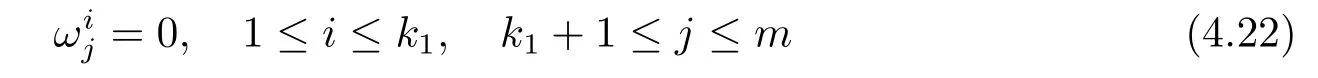
hold identically.Taking exterior differentiation of(4.22)and making use of(2.13),we find that,at p

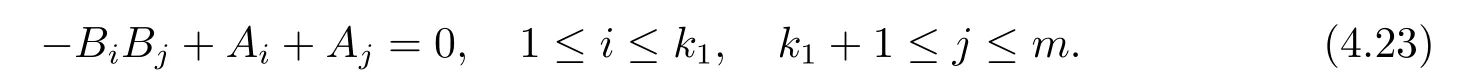
If there exist one pair of indices i0,j0satisfying 1≤i0≤k1,k1+1≤j0≤m such that BiO0 and BjO0,then for each index i satisfying 1≤i≤k1,we obtain

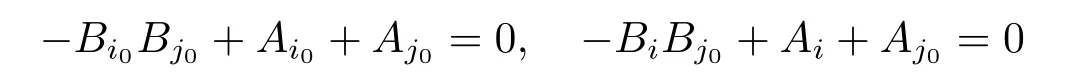
from which it follows that(Bi-BiO)BjO=0,or equivalently Bi=BiO,1≤i≤k1. Similarly,we obtain Bj=BjO,k1+1≤j≤m.Consequently,(4.10)also holds in the case that t=2.Now,an argument similar to that in the proof of Lemma 4.5 shows that the conformal principal curvatures Biare all constant.Therefore B is parallel by(4.22), contradicting to the assumption.Thus either Bi=0 for all indices i satisfying 1≤i≤k1, or Bj=0 for all indices j satisfying k1+1≤j≤m.In both cases we have,by(4.23), λ1+λ2=0.

Proof of Theorem 1.2 By Theorem 1.1 and Theorem 1.2,it clearly suffices to consider the case that x neither is conformal isotropic nor has parallel conformal second fundamental form.Hence from those Lemmas proved in this section,we can suppose without loss of generality that

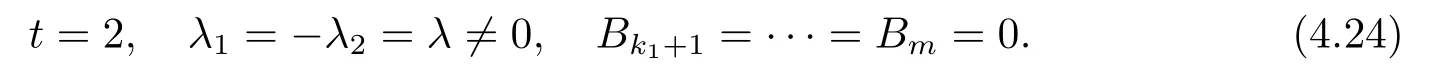
Let{Ei;1≤i≤k1}and{Ej;k1+1≤j≤m}be orthonormal frame fields for subbundles V1and V2,respectively.Then{Ei;1≤i≤m}is an orthonormal frame field on Mmwith respect to the conformal metric g.Then(4.22)implies that both V1and V2are integrable,and thus Riemannian manifold(Mm,g)can be locally decomposed into a direct product of two Riemannian manifolds(M1,g1)and(M2,g2),that is,as a Riemannian manifold,locally

It follows from(2.13),(4.5),(4.24)and(4.25)that the Riemannian curvature tensors of (M1,g1)and(M2,g2)have the following components,respectively,

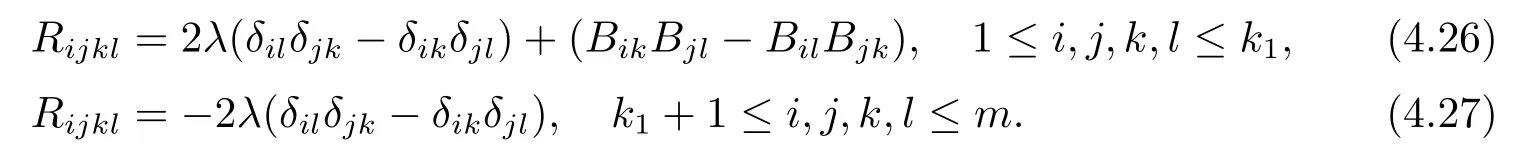
Thus(M2,g2)is of constant sectional curvature-2λ.

Next we consider the following cases separately.

Case(1)λ＞0.In this case,set r=(2λ)-1/2.Then(M2,g2)can be locally identified withbe the canonical embedding.

which has h as its second fundamental form.Clearly,1has constant scalar curvature

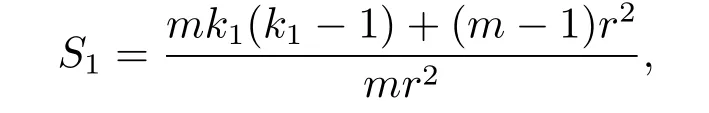
and Mmcan be locally identified with

Case(2)λ＜0.In this case,set r=(-2λ)-1/2,then(M2,g2)can be locally identified with Sm-k1(r).Let2:Sm-k1(r)→Rm-k1+1be the canonical embedding.

which has h as its second fundamental form.Clearly,has constant scalar curvature

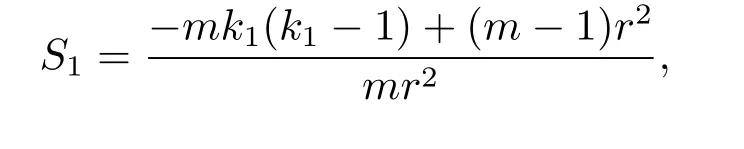
and Mmcan be locally identified with

Assume without loss of generality that00.Define ε=Sgn(0)and let1=ε1/0,2=ε2/0and=(1,2).Then,by the discussion in Example 3.3,:defines a regular space-like hypersurface with the given g and B as its conformal metric and conformal second fundamental form,respectively.It follows by Theorem 2.4 that x is conformal equivalent to.

References

[1]Nie Changxiong,Wu Chuanxi.Space-like hypersurfaces with parallel conformal second fundamental forms in the conformal space(in Chinese)[J].Acta Math.Sinica,Chin.Ser.,2008,51(4):685-692.

[2]Nie Changxiong,Wu Chuanxi.Regular submanifolds in the conformal space[J].Chin.Ann. Math.,2012,33:695-714.

[3]Nie Changxiong,Li Tongzhu,He Yijun,Wu Chuanxi.Conformal isoparametric hypersurfaces with two distinct conformal principal curvatures in conformal space[J].Sci.China Math.,2010,53(4): 953-965.

[4]Hu Zejun,Li Haizhong.Classification of hypersurfaces with parallel Mbius second fundamental form in Sn+1[J].Sci.China Ser.A,2004,47:417-430.

[5]Han Yingbo,Feng Shuxiang.On complete hypersurfaces in hyperbolic space form Hn+1(-1)[J].J. Math.,2013,33(5):767-772.

[6]Hu Zejun,Li Xingxiao,Zhai Shujie.On the Blaschke isoparametric hypersurfaces in the unit sphere with three distinct Blaschke eigenvalues[J].Sci.China Math.,2011:54:2171-2194.

[7]Li Xingxiao,Zhang Fengyun.A classification of immersed hypersurfaces in spheres with parallel Blaschke tensors[J].Tohoku Math.J.,2006,58:581-597.

[8]Li Xingxiao,Zhang Fengyun.Immersed hypersurfaces in the unit sphere Sm+1with constant Blaschke eigenvalues[J].Acta Math.Sinica,Engl.Ser.,2007,23(3):533-548.

[9]Li Xingxiao,Zhang Fengyun.On the Blaschke isoparametric hypersurfaces in the unit sphere[J]. Acta Math.Sinica,Engl.Ser.,2009,25(4):657-678.

李兴校,宋虹儒

(河南师范大学数学与信息科学学院,河南新乡453007)

本文引入两个以de Sitter空间为模型的非齐性坐标来覆盖共形空间.利用球面Sm+1中超曲面的Mbius几何的方法,本文研究了中正则类空超曲面的共形几何.作为其结果,本文对所有具有平行Blaschke张量的正则类空超曲面进行了完全分类.

共形形式;平行Blaschke张量;共形度量;共形第二基本形式;极大超曲面;常数量曲率

MR(2010)主题分类号:53A30;53B25O186

∗date:2015-07-04Accepted date:2016-02-19

Supported by National Natural Science Foundation of China(11171091; 11371018).

Biography:Li Xingxiao(1958-),male,born at Jiyuan,Henan,professor,major in differential geometry.