厄兰极值混合模型的有效估计及其在保险中的应用

殷崔红,林小东,2,袁海丽

(1.厦门大学数学科学学院,福建厦门361005)

(2.多伦多大学统计系,加拿大多伦多M5S 3G3)

(3.武汉大学数学与统计学院,湖北武汉430072)

厄兰极值混合模型的有效估计及其在保险中的应用

殷崔红1,林小东1,2,袁海丽3

(1.厦门大学数学科学学院,福建厦门361005)

(2.多伦多大学统计系,加拿大多伦多M5S 3G3)

(3.武汉大学数学与统计学院,湖北武汉430072)

本文研究了Erlang混合分布和广义帕累托分布混合模型的估计问题.通过引入iSCAD惩罚函数,利用EM算法极大化iSCAD惩罚似然函数的方法,获得了混合序和参数的估计值,计算出有效的度量风险指标value-at-risk(VaR)和tail-VaR(TVaR),通过模拟实验和实际数据说明了模型和算法的有效性.推广了有限Erlang极值混合模型在保险数据拟合中的应用.

极值理论;极值混合模型;iSCAD惩罚;EM算法;似然函数

1　引言

Erlang混合分布广泛应用于保险损失数据的建模,在保险破产理论和保险损失数据的拟合中都有良好的表现.保险破产理论中,当利用混合Erlang分布对保险损失的严重程度建模时,通常关注的一些指标将有明确的解析式,比如无限破产概率,随机破产时刻的拉普拉斯变换等,这方面的研究可参考文献[3,17,21,29];近几年,学者更多关注于将Erlang混合分布用于拟合保险实际损失数据,得到了很多令人满意的分布性质,比如分布函数和矩都有解析式,使得相关的风险测度value-at-risk(VaR)和tail VaR(TVaR)比较容易计算.Verbelen[30]等将双边截断引入Erlang混合分布,计算了再保险合同的纯保费.类似研究见文献[9, 10,19,26,30]等.Lee和Lin[20]提出Erlang混合分布的多元形式,多元混合Erlang分布保留了一元Erlang混合分布的大部分有用的分布性质,同时建模相依性,与copula方法相呼应.关于多元Erlang混合分布的研究见文献[2,16,31,32]等.

混合模型的首要问题是混合序的确定,Lee和Lin[19,30]等都利用BIC来确定Erlang混合分布的序,Yin和Lin[33]提出了一种新的iSCAD惩罚函数,建立惩罚似然函数,运用EM算法给出参数的估计,同时给出了混合序的估计.然而值得注意的是:Erlang分布是轻尾的,用它来拟合重尾数据时可能很难达到预期效果.其次,尾部数据相应的权重一般都很小,公式(3.11)可以看出,权重小于阈值λ的相应Erlang分布都被删除,这不利用保留拟合尾部数据的Erlang分布.为解决这些问题,本文引入极值理论拟合尾部数据,建立Erlang极值混合模型.

极值混合模型广泛应用于各领域的数据分析中,尤其在保险、金融、水文和环境科学等领域.在保险领域,大额索赔在保险公司的风险管理和产品定价,尤其是再保险产品的定价方面,有不可忽略的意义.文献[4,12,13,23,27]等将极值理论引入到保险的风险管理中.为使数据的主体和尾部都拟合的很好,Behrens[5]提出单一参数分布与一个极值分布的混合模型, Carreau和Bengio[7]讨论混合参数分布与极值分布的混合模型,类似的文献[5,6,15,22, 24]等给出多种极值混合模型.Lee[18]等最早将极值混合模型引入到保险数据中,但是所有这些混合模型都没有考虑混合序的确定.

本文建立Erlang混合分布与广义帕累托(GPD)分布的混合模型,广义帕累托(GPD)分布用于拟合数据的尾部,而Erlang混合分布用于拟合数据的主体,这样即有Erlang混合分布的优点,同时保留了极值理论的长处.引入iSCAD惩罚来估计混合Erlang分布的参数, Yin和Lin[33]已证明参数和混合序的估计都有一致性.

2　Erlang极值混合模型

首先给出Erlang分布的密度函数为

其中γ是取值为正整数的形状参数(shape parameter),θ＞0是尺度参数(scale parameter).

将m个不同的Erlang分布以权重α=(α1,···,αm)混合,则Erlang混合分布的密度函数为

相应的分布函数为F(x;α,γ,θ),其中权重参数α=(α1,···,αm)满足αj≥0和γ=(γ1,···,γm)是形状参数,为了可识别性的说明,一般有γ1≤···≤γm,而θ＞0是共有的尺度参数.

由于投保人的性别、车型、驾车经验和熟悉程度等的不同,使得索赔数据一般有明显的异质性,单一的Erlang分布可能很难给出好的拟合效果,因此数据的主体部分本文仍然选用Erlang混合分布来拟合,而尾部采用极值分布.故本文采用左右双边截断的Erlang混合分布,大部分保险损失数据都是已知截断值,比如保险中的免赔额和赔偿限额.以l和µ分别表示左右截断值(免赔额l已知),双边截断的Erlang混合分布的密度函数是

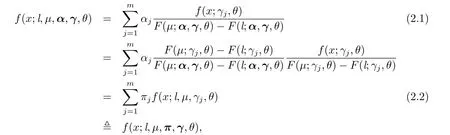
其中

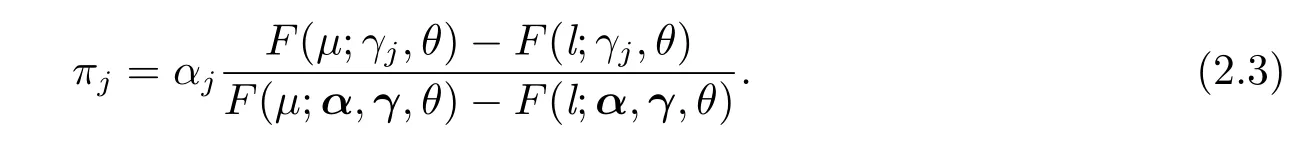
显然,(2.2)式是左右截断点为l和µ的Erlang分布f(x;l,µ,γj,θ)的混合模型,混合权重为π=(π1,···,πm),满足πj≥0和=1.密度函数(2.1)相应的分布函数为F(x;l,µ,α,γ,θ).

在统计中,广义帕累托分布(Generalized Pareto Distribution,i.e.,GPD)经常被用于拟合其他分布或实际数据的尾部,本文选用GPD拟合数据的尾部,其密度函数是

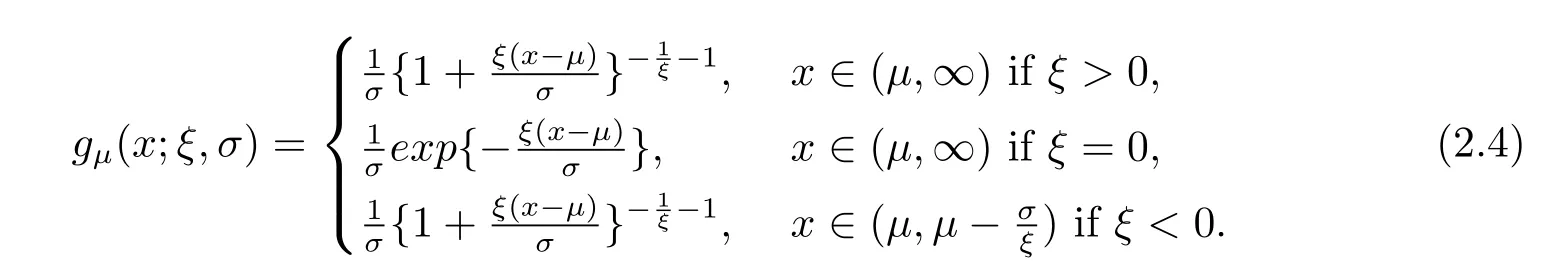
广义帕累托分布(GPD)的生存函数为

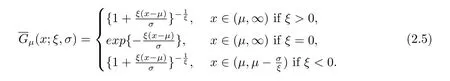
结合(2.1)和(2.4)式,为弥补引言中提过的Erlang混合模型的不足,本文建立的Erlang极值混合模型的密度函数为

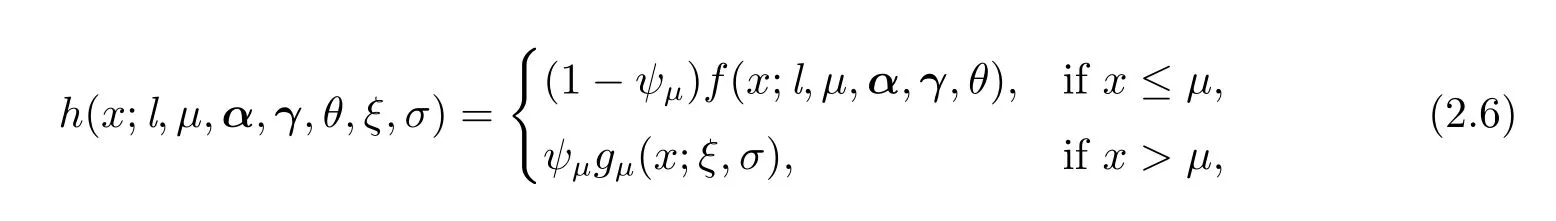
其中µ为阈值,X是服从h(x;l,µ,α,γ,θ,ξ,σ)分布的随机变量,令ψµ=P(X＞µ),其一般由大于µ的样本比例来估计.

相应的生存函数为

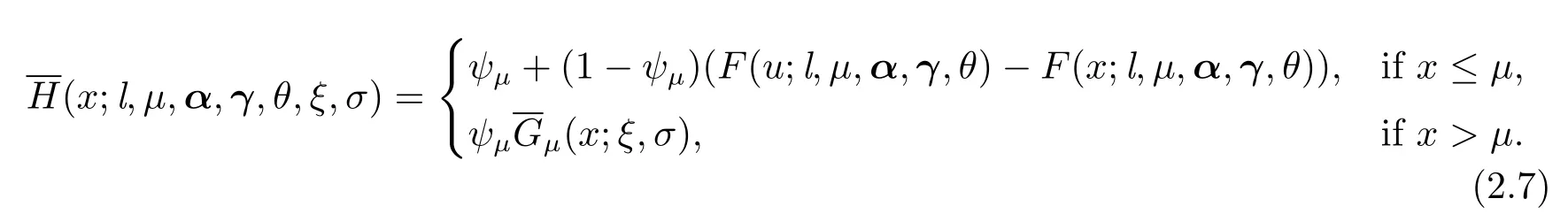
风险测度就是各种风险度量指标的总称.现行的国际标准风险管理工具VaR最初由Morgan针对银行业务风险的需要提出的,并很快被推广成为了一种产业标准.风险价值VaR是指在正常的市场条件、给定的置信水平以及给定的持有期间内,投资组合所面临的潜在最大损失.VaR是一种分位数风险测度,一般给定置信水平p,典型的p=95%或者99%.但是,VaR作为风险测度只考虑了概率为p的事件的最大损失VaRp,高于VaRp的损失并没有纳入风险测度,为克服这个缺陷,Tail Value at Risk(or TVaR)被提出来.在给定置信水平p下,TVaR就是损失落入最糟的1-p部分的平均损失.下面给出Erlang极值混合模型关于风险指标VaR和TVaR的计算.

为便于风险指标VaRp和TVaRp的计算,当X≤µ时,将生存函数(2.7)用Erlang密度函数分别表达为

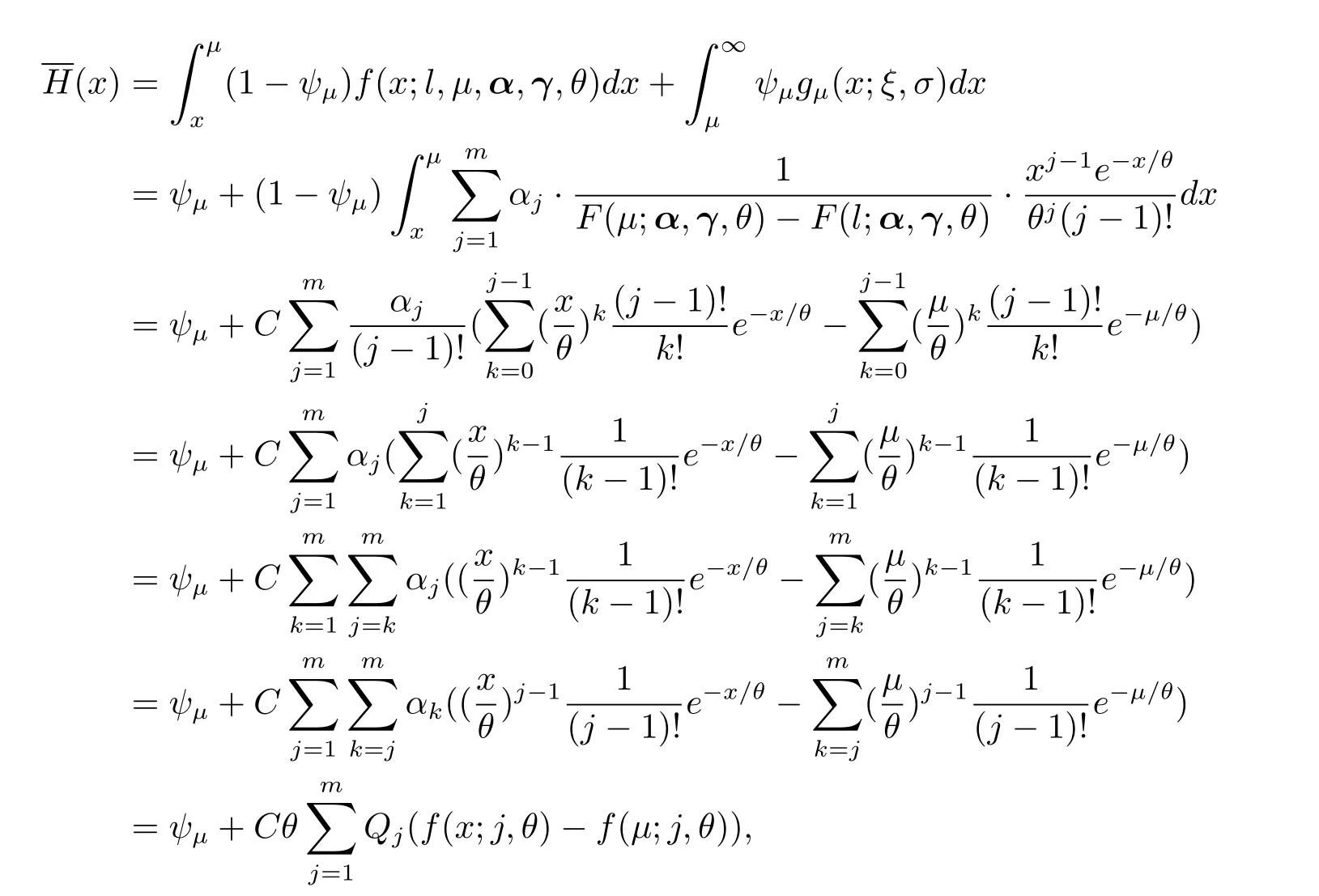
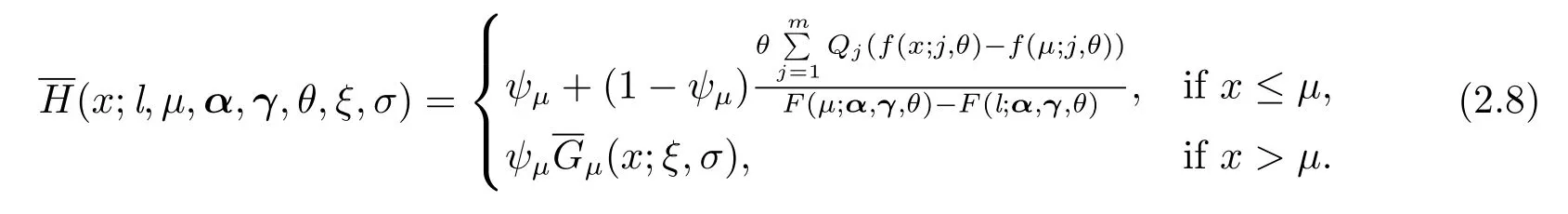
假设损失随机变量X服从Erlang极值混合分布(2.6),给定置信水平p,有

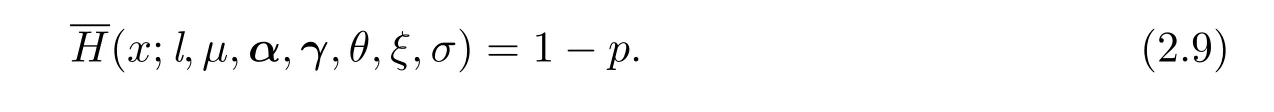
方程(2.9)的解即置信水平为p的VaRp.

计算TVaRp之前,首先研究自付责任额为R(＞l)的再保险的纯保费,当R≤µ时,

当R＞µ时,

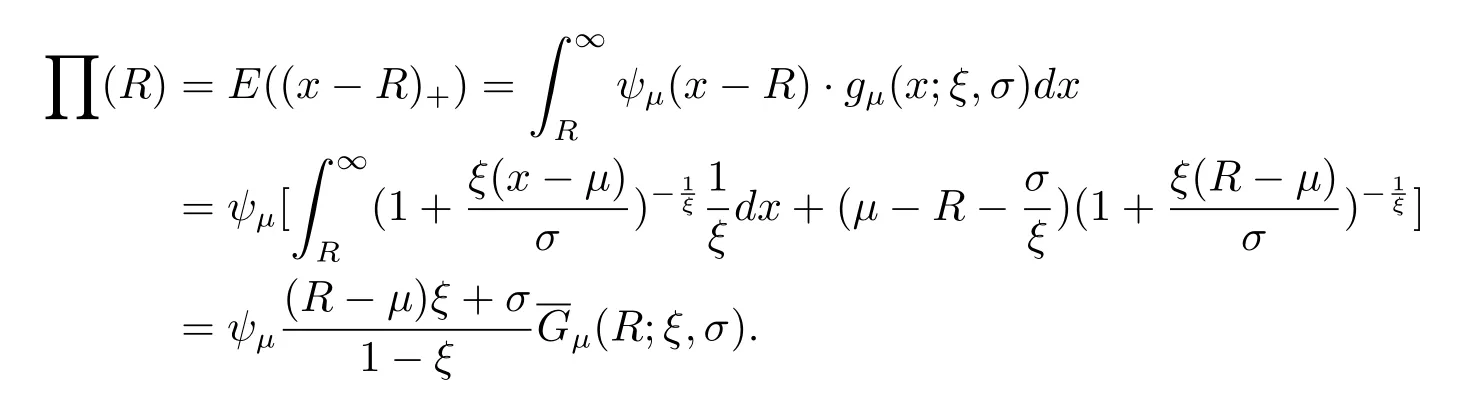
综上,自付责任额为R(＞l)的再保险的纯保费为

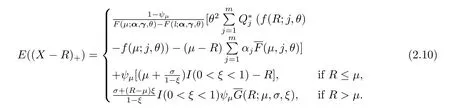
当自付责任额R=VaRp时,置信水平为p的TVaRp为

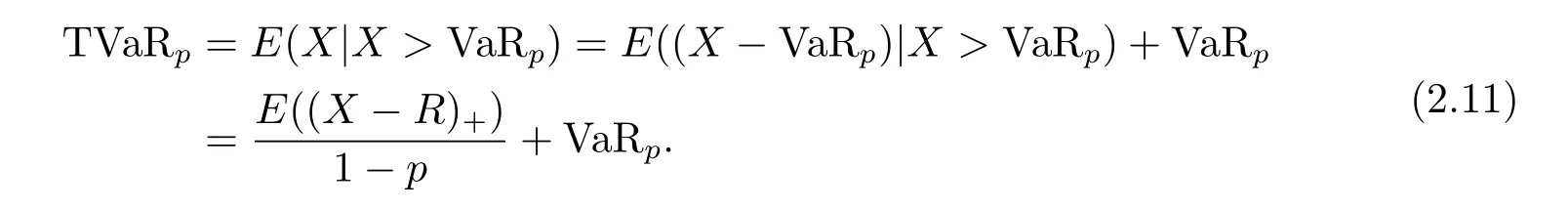
3　EM算法

文献[33]针对每一个分量权重参数πj,j=1,···,m,提出的iSCAD惩罚函数为

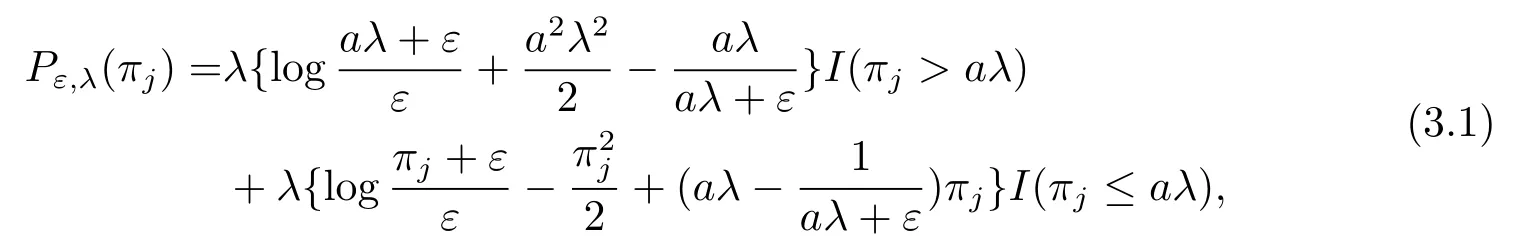
其中I(·)是示性函数.本文建立的Erlang极值混合分布中Eralng混合分布的参数估计与新引入的极值分布的参数估计互不影响,因此关于Eralng混合分布的极大惩罚似然估计仍然是一致的.

Expectation-Maximization(EM)算法最早由Dempster[11]给出比较详细的说明,当似然函数的最大值点不能直接得到时,EM算法通过迭代的方法找到最大值点.EM算法需引入隐变量,隐变量可以是未知参数,丢失的数据或者任何可以使模型简化的未观测数据量. EM算法分为E-step和M-step两步,其中E-step计算目标函数关于隐变量Z的条件期望, M-step是最大化目标函数,求得参数的极大似然估计.王继霞等[1]将EM算法用于有限混合Laplace分布的估计.

Erlang极值混合模型的所有待估参数是:拟合数据主体部分的Erlang混合分布的序m,形状参数γ=(γ1,···,γm),相应的权重参数α=(α1,···,αm),所有Erlang分布共用的尺度参数θ,拟合数据尾部的广义帕累托分布的阈值µ,尺度参数σ,形状参数ξ,下面逐一介绍它们的估计.

由公式(2.2)知,密度函数(2.6)也可以由新权重参数π表示为

假设X=(X1,···,Xn)是独立同分布的随机变量,服从密度函数h(x;l,µ,π,γ,θ,ξ,σ),即(3.2),样本观测值为x=(x1,···,xn),相应有序样本观测值为x(1)≤···≤x(n),记

Pickands[25]给出与阈值µ相应的k的选择方法,从1开始依次增加,最大值为[n/4],而µ=x(n-k),本文最终由似然函数的大小选出µ.为方便后面的说明,重新表示n＇=n-k和x＇=(x(1),···,x(n＇)).

形状参数的估计采用Yin和Lin[33]类似的方法,即预先给定一个大的混合序M,形状参数的所有可能取值是γ0=(),通过估计相应的权重参数,来实现混合序的估计和形状参数的选择.

Erlang极值混合分布的密度函数h(x;l,µ,π,γ0,θ,ξ,σ)中的部分未知参数记为φ= (π1,···,πM,θ),本文采用EM算法来估计φ.

样本x=(x1,···,xn)的对数似然函数为

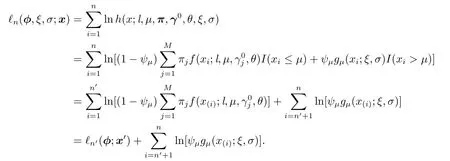
样本x=(x1,···,xn)的iSCAD惩罚对数似然函数,其中与参数φ=(π1,···,πM,θ)有关的部分是

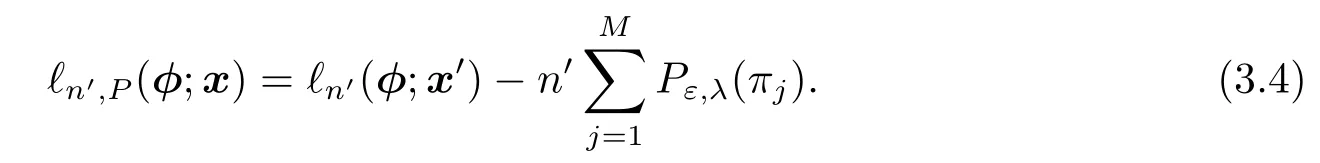
直接关于ℓn＇,P(φ;x)求极大似然估计是困难的,本文使用EM算法,引入隐变量,即Z=(Z1,···,Zn),其中Zi=(Zij|i=1,···,n,j=1,···,M),

那么完整样本(x,Z)的似然函数为

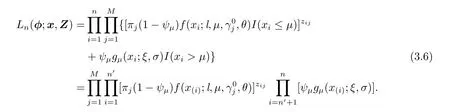
相应完整样本(x,Z)的对数似然函数为

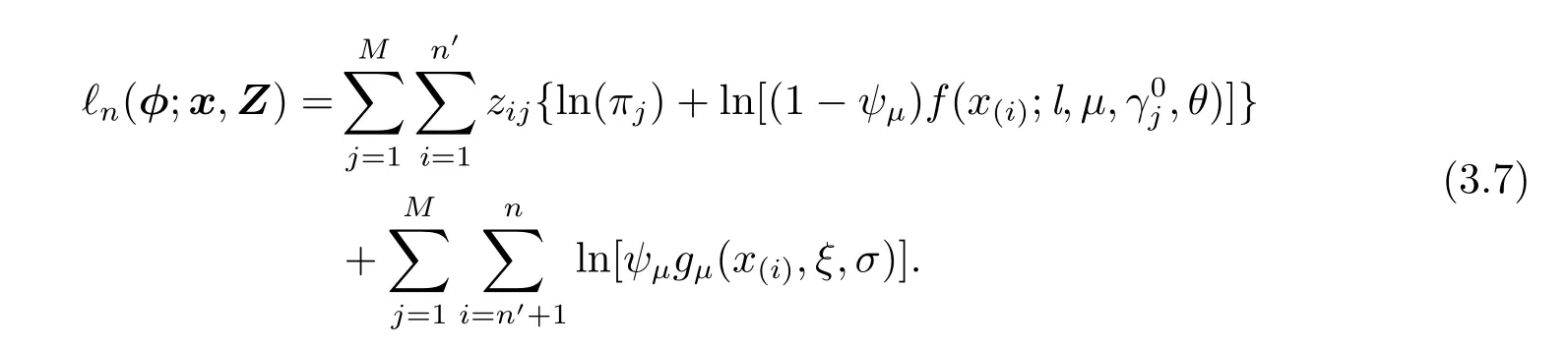
相应的完整样本(x,Z)的iSCAD惩罚对数似然函数为

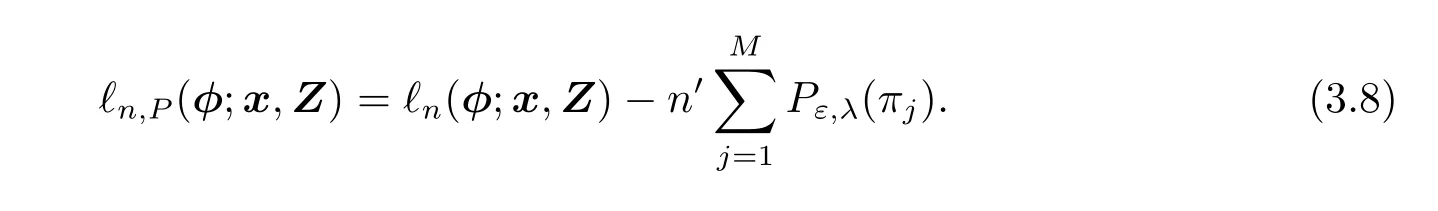
EM算法是利用迭代过程来估计参数的方法,假设已经完成第k次迭代,获得的当前估计是φ(k)=EM算法的E-step和M-step分别为

E-step ℓn,P(φ;x,Z)关于隐变量Z求条件期望,得到关于可观测样本x的边际似然函数,即

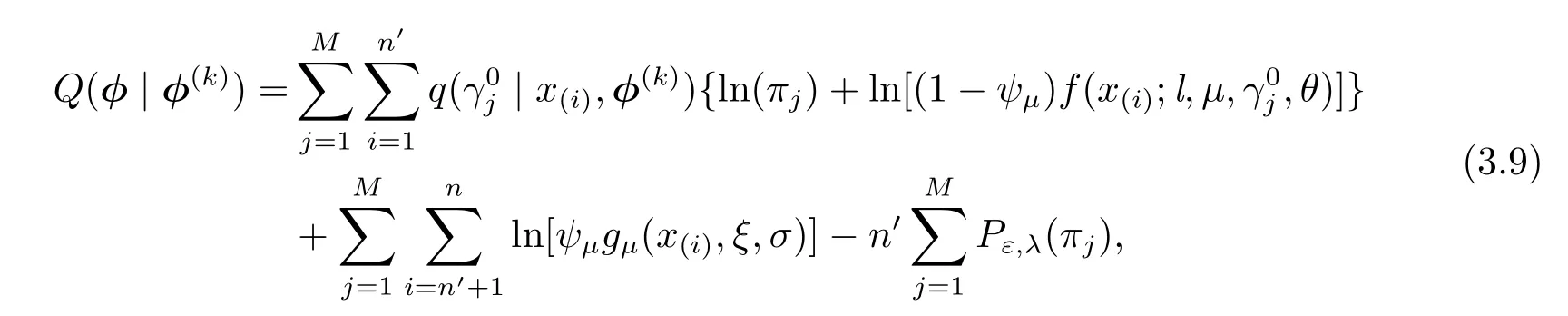
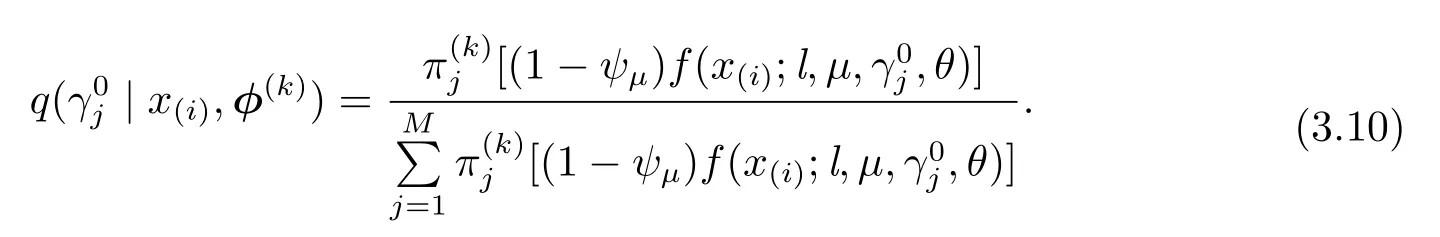
M-step(3.9)式是权重参数πj(j=1,···,M)和尺度参数θ的函数,求函数(3.9)的极大估计,即

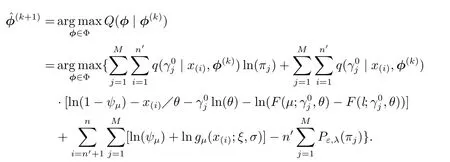
权重参数πj的第(k+1)次迭代的估计为

尺度参数θ的第(k+1)次迭代的估计为

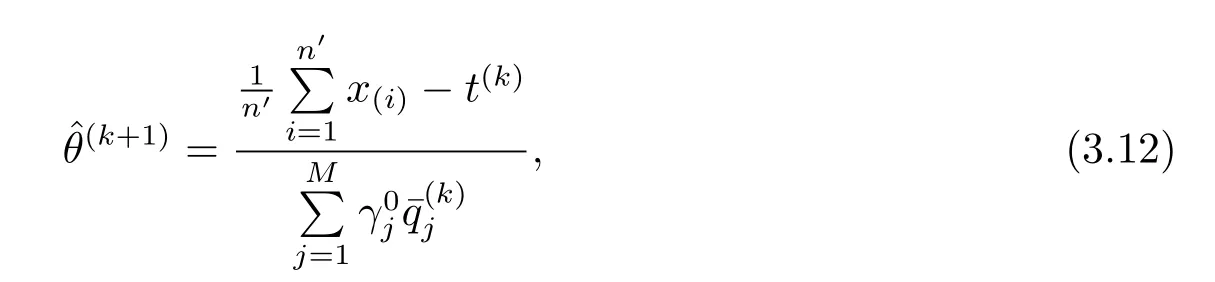
其中

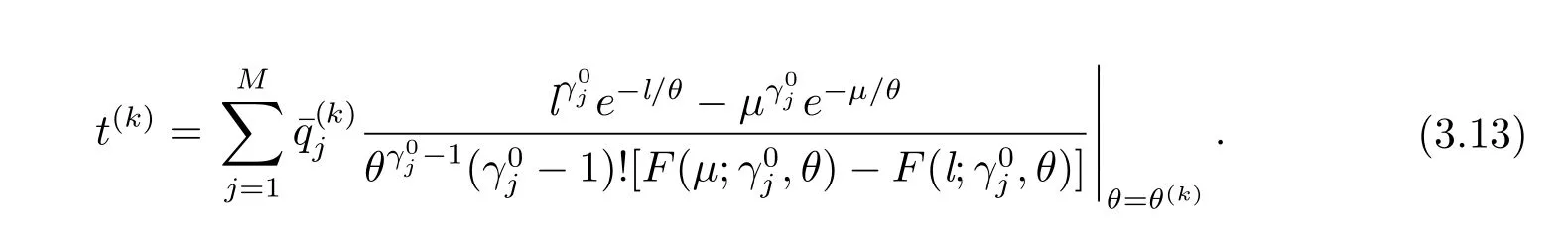
迭代过程一直持续到|Q(φ(k))-Q(φ(k-1))|小于某个既定的误差界.分别以0,j=1,···,M}和表示EM迭代的最终结果.混合模型序的估计是

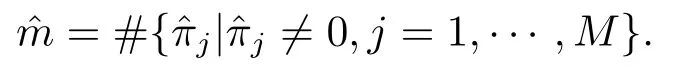
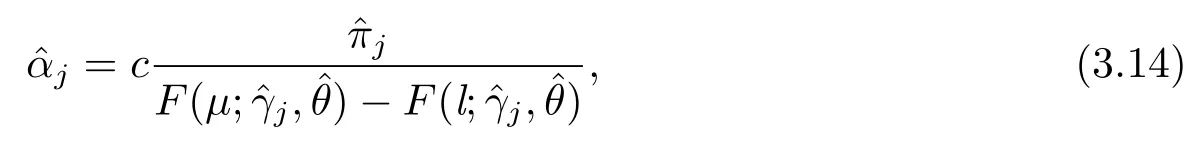
最后,关于广义帕累托分布(GPD)的尺度参数σ和形状参数ξ的极大似然估计,Coles[8]已经详细讨论过,本文就不再作重复说明.

本文利用R软件进行计算,基于Yin和Lin[33]关于Erlang混合分布的R程序和软件包“ismev”,编写本文Erlang混合分布和GPD分布混合模型的R程序,完成模拟实验和实际数据中模型参数的估计.

4　模拟实验

为验证模型和估计的有效性,本文给出一个模拟实验,从密度函数(2.6)中随机抽取了2500个随机数,其中(2.6)式中的所有参数见表1中的真实参数.

表1:真实参数与参数估计值的对比

参数的初始化主要参考文献[19,28].事先给定M=10,形状参数的备择范围即γ=(1,···,10),以Tijms[28]的方法初始化,公式(3.11)给出极大惩罚似然的权重参数估计,其稀疏性实现了在形状参数备择范围γ=(1,···,10)中进行合理选择.从表1可以看出,形状参数最终仅选中=(2,7),只有这两个形状参数对应的权重参数估计为非零的,即=(0.501,0.499),其它形状参数相应的权重参数估计均为零,即=0,j=1,3,4,5,6,8,9,10.显然,混合模型序的估计

由本实验可以看出,引入iSCAD惩罚的优势所在:通过对权重参数的估计,同时实现了对形状参数的选择和混合模型序的估计.表1列出的所有参数估计值与真实值都很接近,说明模型和算法都很有效,能够反映出数据的特征.图1很好的反应了这一点,图1中的真实曲线和拟合曲线几乎是重合的.

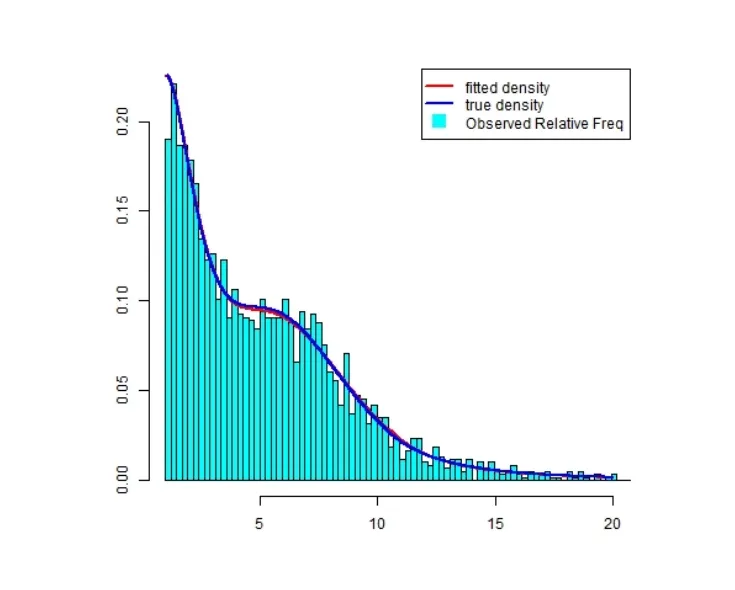
图1:模拟数据的直方图,真实曲线与拟合曲线

5　丹麦火灾数据

丹麦火灾赔偿数据有2167个观测值,Embrechts[14]和Mendes[24]等都用极值理论研究过这组数据的尾部,本文采用Erlang极值混合模型从总体上研究这组数据,不再仅仅限于研究其尾部特征.

文献[33]讨论了带左截断点l的Erlang混合分布,本文在其基础上提出了Erlang极值混合分布,在本例中将利用这两种不同的分布分别拟合丹麦火灾赔偿数据,比较两种分布的优劣.

表2给出Erlang混合分布和Erlang极值混合分布(2.6)拟合火灾损失数据得到的所有参数的估计值,其中利用Erlang极值混合分布得到的结果说明拟合数据的主体部分采用了三个Erlang分布,数据的尾部由广义帕累托分布来拟合,两部分的阈值点为4.174,尾部数据比例为0.152;而利用Erlang混合分布拟合同一组火灾数据则需要十个不同的Erlang分布的混合.

表2　:参数估计值

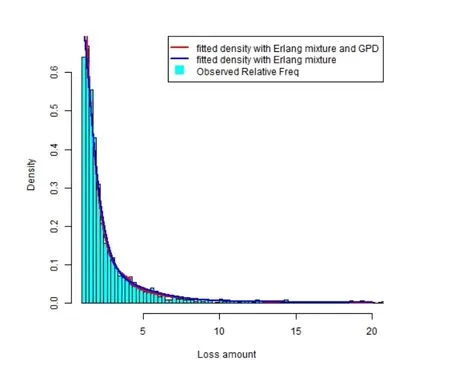
图2:丹麦火灾数据的直方图与拟合曲线

图2是丹麦火灾数据的直方图、Erlang混合分布和Erlang极值混合分布的拟合曲线,可以看出拟合效果较好.

图3和4分别给出Erlang混合分布和Erlang极值混合分布的Q-Q图,显然Erlang极值混合分布在尾部数据的拟合上更优.

本文给出VaR的非参数(nonparametric)法估计作为标杆,在置信水平为p的条件下, VaRp的非参数估计是方程Fn(VaRp)=p的解,其中Fn(x)=

表3:非参数法、Erlang混合分布和Erlang极值混合分布的VaRp值的比较

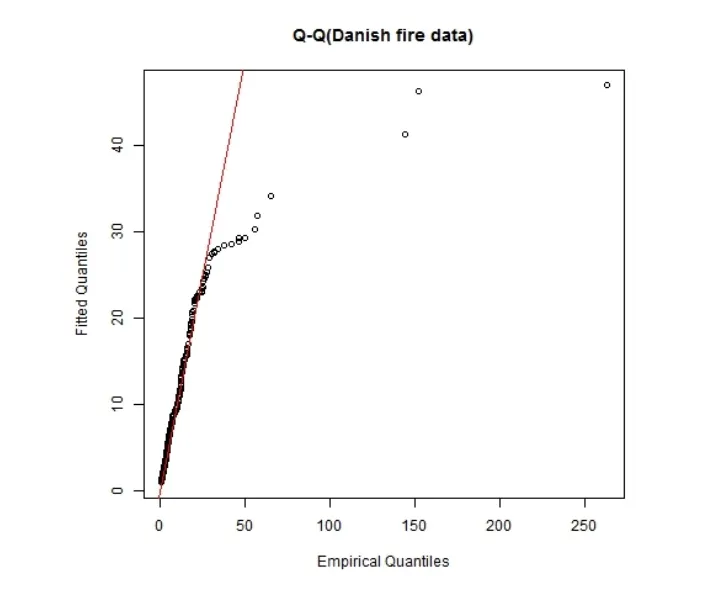
图3:丹麦火灾数据的Q-Q图(Erlang混合分布)

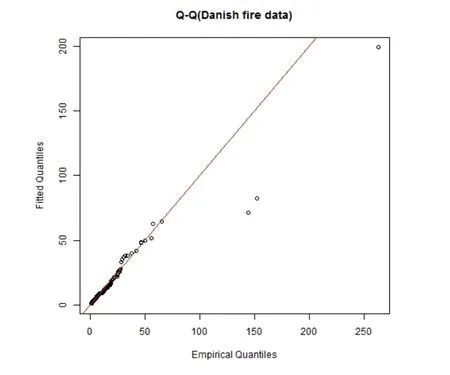
图4:丹麦火灾数据的Q-Q图(Erlang极值混合分布)

表3给出三种方法的VaRp估计值,表3可以看出,Erlang极限混合分布估计得到的VaRp与非参数法得到的VaRp非常接近,估计效果很好.

表4:非参数法、Erlang混合分布和Erlang极值混合分布的TVaRp值的比较

表4给出非参数法、Erlang混合分布和Erlang极值混合分布的TVaRp估计值,其中TVaR的非参数估计为TVaRp=.Erlang混合分布的TVaRp比非参数法的结果偏小,这主要是因为Erlang混合分布对火灾损失数据的尾部拟合不足,见图3;而Erlang极值混合分布的结果稍大,而且越到尾部,这种趋势越明显,这主要是因为估计得到的=0.661＞0,即估计的极值分布为厚尾的,而实际数据的尾部过于稀疏,不足以表现这种厚尾性.

[1]王继霞,汪春峰,苗雨.有限混合Laplace分布回归模型局部估计的EM算法(英文)[J/OL].数学杂志, 2016,36(4):667-675.

[2]Badescu A L,Lan G,Lin X S,et al.Modeling correlated frequencies with application in operational risk management[J].J.Oper.Risk,2015,10(1):1-43.

[4]Beirlant J,Goegebeur Y,Segers J,et al.Statistics of extremes:theory and applications[M].Ltd England:John Wiley&Sons,2006.

[5]Behrens C N,Lopes H F,Gamerman D.Bayesian analysis of extreme events with threshold estimation[J].Stat.Model.,2004,4(3):227-244.

[6]Carreau J,Bengio Y.A hybrid Pareto model for asymmetric fat-tail data[R].Technical Report 1283, Canada:Dept.IRO,Universitde Montral,2006.

[7]Carreau J,Bengio Y.A hybrid pareto mixture for conditional asymmetric fat-tailed distributions[J]. Neural Net.,IEEE Trans.,2009,20(7):1087-1101.

[8]Coles S,Bawa J,Trenner L,et al.An introduction to statistical modeling of extreme values[M]. London:Springer,2001.

[9]Cossette H,Mailhot M,Marceau.TVaR-based capital allocation for multivariate compound distributions with positive continuous claim amounts[J].Insur.:Math.Econ.,2012,50(2):247-256.

[10]Cossette H,CotM P,Marceau E,et al.Multivariate distribution defined with Farlie Gumbel Morgenstern copula and mixed Erlang marginals:Aggregation and capital allocation[J].Insur.: Math.Econ.,2013,52(3):560-572.

[11]Dempster A P,Laird N M,Rubin D B.Maximum likelihood from incomplete data via the EM algorithm[J].J.Royal Stat.Soc.,Ser.B(Methodological),1977:1-38.

[12]Embrechts P,Klppelberg C,Mikosch T.Modelling extremal events for insurance and finance[J]. Springer,1997,71(2):183-199.

[13]Embrechts P,Resnick S I,Samorodnitsky G.Extreme value theory as a risk management tool[J]. North Amer.Actua.J.,1999,3(2):30-41.

[14]Embrechts P,Klppelberg C,Mikosch T.Modelling extremal events:for insurance and finance[M]. Germany:Springer Sci.Business Media,2013.

[15]Frigessi A,Haug O,Rue H.A dynamic mixture model for unsupervised tail estimation without threshold selection[J].Extremes,2002,5(3):219-235.

[16]Hashorva E,Ratovomirija G.On Sarmanov mixed Erlang risks in insurance applications[J].Astin Bull.,2015,45(01):175-205.

[17]Landriault D,Willmot G E.On the joint distributions of the time to ruin,the surplus prior to ruin, and the deficit at ruin in the classical risk model[J].North Amer.Actua.J.,2009,13(2):252-270.

[18]Lee D,Li W K,Wong T S T.Modeling insurance claims via a mixture exponential model combined with peaks-over-threshold approach[J].Insur.:Math.Econ.,2012,51(3):538-550.

[19]Lee S C K,Lin X S.Modeling and evaluating insurance losses via mixtures of Erlang distributions[J]. North Amer.Actua.J.,2010,14(1):107-130.

[20]Lee S C K,Lin X S.Modeling dependent risks with multivariate Erlang mixtures[J].Astin Bull., 2012,42(01):153-180.

[21]Lin X S,Willmot G E.The moments of the time of ruin,the surplus before ruin,and the deficit at ruin[J].Insur.:Math.Econ.,2000,27(1):19-44.

[22]MacDonald A,Scarrott C J,Lee D,et al.A flexible extreme value mixture model[J].Comput.Stat. Data Anal.,2011,55(6):2137-2157.

[23]McNeil A J.Estimating the tails of loss severity distributions using extreme value theory[J].Astin Bull.,1997,27(01):117-137.

[24]Melo Mendes B V,Lopes H F.Data driven estimates for mixtures[J].Comput.Stat.Data Anal., 2004,47(3):583-598.

[25]Pickands III J.Statistical inference using extreme order statistics[J].Ann.Stat.,1975:119-131.

[26]Porth L,Zhu W,Seng Tan K.A credibility-based Erlang mixture model for pricing crop reinsurance[J].Agricul.Finance Rev.,2014,74(2):162-187.

[27]Resnick S I.Discussion of the Danish data on large fire insurance losses[J].Astin Bull.,1997,27(01): 139-151.

[28]Tijms H C.A first course in stochastic models[M].UK:John Wiley and Sons,2003.

[29]Tsai C C L,Willmot G E.On the moments of the surplus process perturbed by diffusion[J].Insur.: Math.Econ.,2002,31(3):327-350.

[30]Verbelen R,Gong L,Antonio K,et al.Fitting mixtures of Erlangs to censored and truncated data using the EM algorithm[J].Astin Bull.,2015,45(03):729-758.

[31]Verbelen R,Antonio K,Claeskens G.Multivariate mixtures of Erlangs for density estimation under censoring[J].Life.Data Anal.,2015:1-27.

[32]Willmot G E,Woo J K.On some properties of a class of multivariate Erlang mixtures with insurance applications[J].Astin Bull.,2015,45(01):151-173.

[33]Yin C,Lin X S.Efficient estimation of Erlang mixtures using iSCAD penalty with insurance application[J].Astin Bull.,Available on CJO2016,doi:10.1017/asb.2016.14.

2010 MR Subject Classification:62E15;62F10

EFFICIENT ESTIMATION OF ERLANG AND GPD MIXTURES USING ISCAD PENALTY WITH INSURANCE APPLICATION

YIN Cui-hong1,LIN Xiao-dong1,2,YUAN Hai-li3
(1.School of Mathematical Sciences,Xiamen University,Xiamen 361005,China)
(2.Department of Statistical Sciences,University of Toronto,Ontario M5S 3G3,Canada)
(3.School of Mathematics and Statistics Sciences,Wuhan University,Wuhan 430072,China)

In this paper,we study efficient estimation of Erlang&GPD mixture model.By using a new thresholding penalty function and a corresponding EM algorithm,we estimate model parameters and determine the order of the mixture model.We obtain risk measure including VaR and TVaR and show efficiency of the new mixture model in simulation studies and a real data application,which improve Erlang&extreme value mixture model in modeling insurance losses.

extreme value theory;mixture model;iSCAD penalty;EM algorithm;likelihood function

MR(2010)主题分类号:62E15;62F10O212.1

A

0255-7797(2016)06-1315-13

∗2016-04-09接收日期:2016-06-28

国家自然科学基金资助(11201352).

殷崔红(1982-),女,山东潍坊,博士,主要研究方向:非寿险精算.