基于隐式PIGPC的网络控制系统时延补偿方法

田中大， 李树江， 王艳红

(沈阳工业大学 信息科学与工程学院,辽宁 沈阳 110870)



基于隐式PIGPC的网络控制系统时延补偿方法

田中大， 李树江， 王艳红

(沈阳工业大学 信息科学与工程学院,辽宁 沈阳 110870)

网络控制系统的时延会导致系统性能下降，针对该问题提出一种基于隐式PIGPC的时延补偿方法。首先，通过历史时延数据，利用自适应变步长最小均方滤波算法对当前时刻的网络时延进行预测，将预测时延代替实际时延作为时延补偿控制器的参数。然后为改进隐式GPC的时延补偿效果，提出具有PI结构的隐式PIGPC算法。隐式PIGPC不必递推求解Diophantine方程，可节省在线计算时间，并且把PI的反馈结构与GPC的预测功能结合起来，改善了控制器的性能。利用隐式PIGPC设计控制器，结合预测时延完成基于隐式PIGPC的网络时延补偿控制器的设计,并对时延补偿算法的稳定性进行了分析。最后的仿真实验表明隐式PIGPC对网络控制系统时延具有良好的补偿效果，同时具有较少的运算时间。

网络控制系统；时延补偿；时延预测；隐式PIGPC

0 引 言

网络控制系统(NCS)是传感器、执行器和控制器之间信号通过网络传输的全分布、网络化的实时反馈控制系统。由于控制回路中网络的引入，使得NCS的分析变得复杂[1-2]，最明显的一个问题是网络诱导时延的引入，这对网络控制系统的性能产生影响，甚至造成不稳定[3]，因此非常有必要对网络控制系统中的随机时延进行补偿。

针对网络控制系统中的时延补偿问题，目前已有了大量的研究成果。很多学者采用不同的方法对网络控制系统时延进行补偿，包括智能控制[4-5]，鲁棒控制[6-7]，预测控制[8-10]等都得到了广泛的应用。但已有时延补偿算法存在过于复杂、计算量大或者对模型要求精确等缺点。而广义预测控制(GPC)是从自适应控制的研究中发展起来的预测控制算法，克服了模型不能描述不稳定过程和难以在线辨识的缺点，呈现优良的控制性能和鲁棒性，被广泛地应用于工业过程控制中，这些特点使得GPC非常适合对网络控制系统进行时延补偿。文献[11]利用AR回归模型对时延进行预测，同时采用改进的GPC算法对时延补偿。文献[12]基于时变网络随机时延，采用基于状态空间模型的网络广义预测控制，获得了有效的跟踪性能。文献[13]给出了在前向通道和反馈通道都有随机时延的情况下的预测控制方法，并且给出了闭环预测控制系统稳定的条件。但是标准的GPC算法需要Diophantine方程求解和矩阵求逆等运算而导致在线计算量过大，从而增加了计算时间, 降低了系统的实时性。

为了提高网络控制系统时延补偿效果，本文利用历史网络时延值，通过一种变步长最小方差(LMS)自适应滤波算法对时延进行预测，该预测算法具有很好的预测精度与实时性。同时在标准的GPC基础上进行改进，提出具有PI结构的隐式GPC算法(隐式PIGPC)对网络时延进行补偿。隐式PIGPC不必递推求解Diophantine方程，可节省在线计算时间，并且把PID的反馈结构与GPC的预测功能结合起来。结合预测时延，可确定执行器需要的输出控制量，达到更好的控制效果。利用True Time进行了无干扰无丢包、有干扰无丢包、既有干扰又有丢包三种情况的仿真，结果验证了本文时延补偿方法的有效性。

1 网络控制系统时延预测方法

1.1 问题描述

如图1所示，在网络控制系统中，从时延产生的不同过程来看，系统中的时延包括[14]：传感器到控制器时延τsc、控制器到执行器时延τca、控制器计算时延τc。其中：τsc和τca分别是NCS前向通道和反馈通道的传输时延；τsc是控制器计算控制量之前产生的，可通过补偿策略加以消除；而τca是控制器计算控制量之后产生的，无法测量，因此必须通过合适的方法对τca进行预测。

为方便研究，做如下假设：

1)网络控制系统中各节点时钟同步，目前已经可实现精确的网络时钟同步。

2)控制系统回路中的数据均采用单包传输。

3)传感器与执行器采用时钟驱动方式，控制器采用事件驱动方式。

4)由于硬件的发展，忽略系统中计算时延τc，同时由于(3)中的驱动方式，则系统在k时刻的总时延τ(k)可视为τsc和τca之和[11]。也即对τ(k)进行预测。

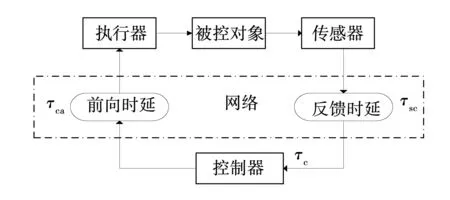
图1 网络时延的组成Fig.1 Composition of network time-delay

同时在数据传输中，受到时延影响，会出现数据包乱序、冲突以及丢失等情况，利用时间戳机制重构数据序列，控制器可辨别最新采样数据，同理执行器也可识别最新的控制数据执行对应的动作。另外，在执行器节点设定缓冲区，存储控制算法计算得到的最新控制量，保证系统控制的准确性。

一般情况下，在k时刻，由传感器到控制器时延τsc(k)是可测的，而控制器到执行器时延τca(k)是未知的，但是k时刻之前是已知的，所以可以使用之前网络时延预测当前网络时延。在消息中增加时间戳，由于网络各节点同步，因此可以得到历史网络时延数据，同时由于时延可以合并进行分析，选择合适的算法即可对系统总时延τ(k)进行预测，得到当前时刻网络的预测时延。

1.2 变步长自适应滤波时延预测算法

自适应滤波算法在系统辨识领域得到了广泛的应用，图2为自适应滤波器的原理图。由于噪声信号v(k)的存在，产生一个对未知系统输出信号d(k)的估计值y(k)，两者之差的误差信号e(k)用于修正自适应滤波器参数来逼近未知系统。目前各种自适应滤波算法中，LMS由于计算量小得到了广泛应用，但是LMS采用固定迭代步长，存在收敛速度与收敛精度之间的矛盾，因此很多的变步长自适应滤波算法被相继提出。

图2 自适应滤波原理图Fig.2 Schematic diagram of adaptive filtering

时延预测算法将网络控制系统时延看作一未知系统，利用变步长自适应LMS滤波算法[15]去逼近该未知系统。设当前时刻为k，控制器中存储了k-1时刻到k-N时刻的网络时延值，时延序列表示为T(k-1)，表达式如下:

T(k-1)=[τ(k-1),τ(k-2),…,τ(k-N)]。

(1)

(2)

采用变步长自适应LMS滤波算法调节调节权重W(k)，其算法如下：

(3)

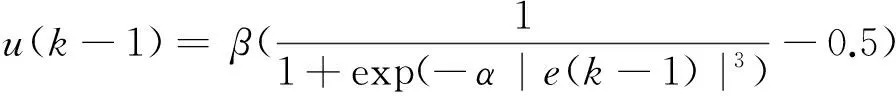
(4)

W(k)=W(k-1)+2u(k-1)e(k-1)T(k-1)。

(5)

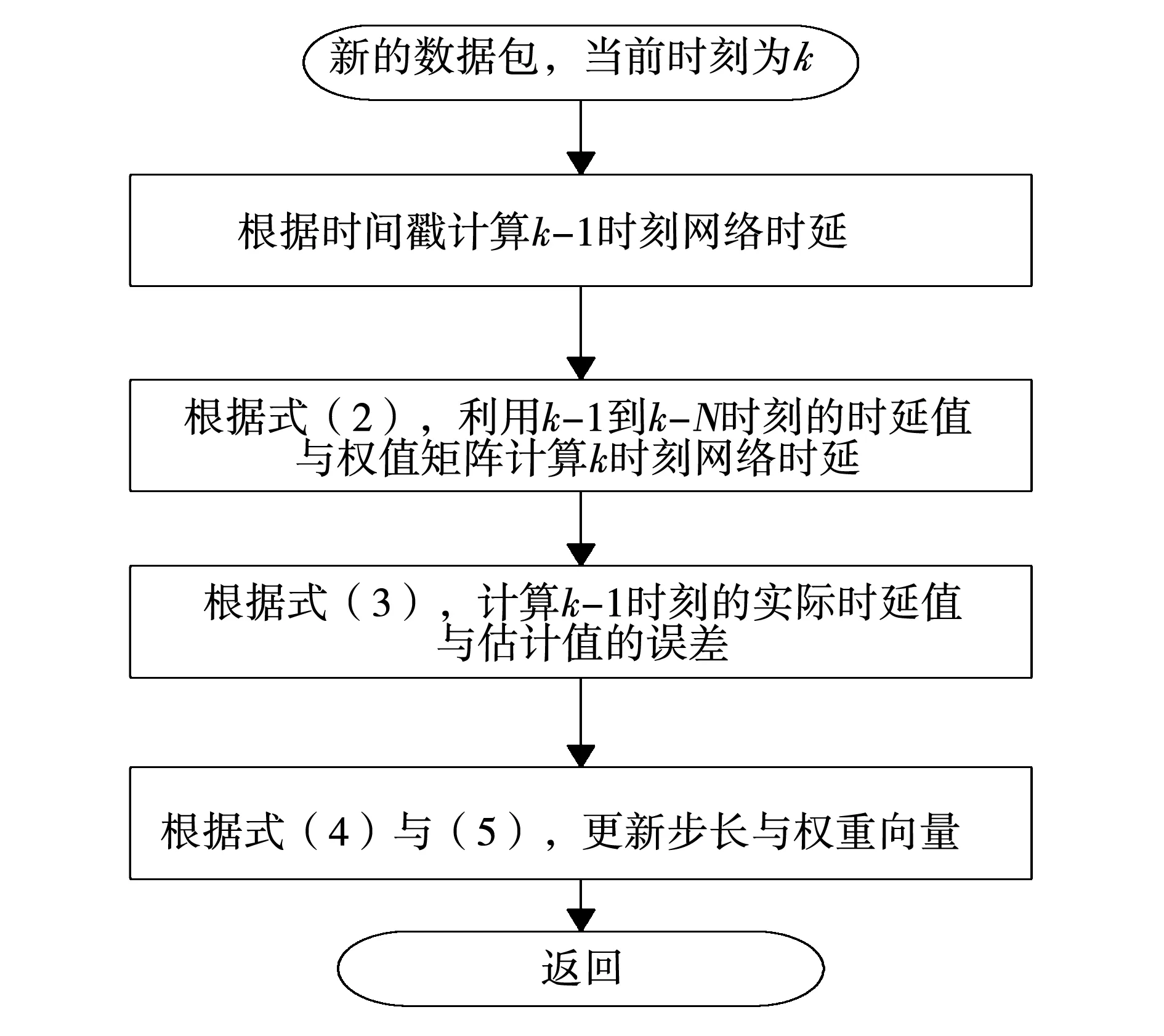
图3 网络时延预测算法Fig.3 Prediction algorithm of network time-delay

2 隐式PIGPC算法及其稳定性分析

2.1 隐式PIGPC算法

广义预测控制直接辨识原系统模型参数，则需在线递推计算Diophantine方程，解出控制器参数，才能求解控制规律，这样计算时间较长。隐式广义预测控制是一种直接辨识控制器参数G和f，而不必递推求解Diophantine方程的隐式算法[17-18]，可节省在线计算时间。

标准的广义预测控制为获得系统输出预测值，需要求解如下的两组Diophantine方程：

1=A(q-1)ΔEj(q-1)+q-jFj(q-1)，

(6)

Ej(q-1)B(q-1)=Gj(q-1)+q-jHj(q-1)。

(7)

式中：q-1为后移算子；A(q-1)，B(q-1)为后移算子的多项式；Ej、Fj、Gj、Hj是由A(q-1)和预测长度j唯一确定的多项式。

由标准GPC的最优控制律

ΔU=(GTG+λI)-1GT(w-f)。

(8)

要求解ΔU必须知道矩阵G和开环预测向量f，隐式GPC就是利用输入输出数据，根据预测直接辨识G和f的算法。根据最优控制律有j个并列预测控制器为：

由上式可知，矩阵G中的所有元素都在最后一个方程中出现，因此仅对上式的最后一个方程辨识即可求得矩阵G。避免了Diophantine方程的递推求解。

为进一步改善网络控制系统的时延补偿效果，在隐式GPC的基础上进行改进，提出具有PI结构的隐式GPC算法(隐式PIGPC)。隐式PIGPC结合PI控制与隐式GPC控制二者之长处，即把PI的反馈结构与GPC的预测功能结合起来，提出了更具有鲁棒性、更宜于工业应用的自适应控制器。这种算法仍是基于模型预报的，但是通过采用新的目标函数，可以获得一种具有PI结构的预测控制算法，以改善控制器性能。

隐式GPC控制算法采用如下目标函数：

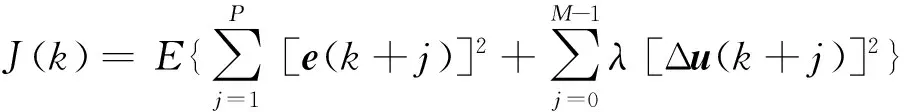
(9)

其中误差序列为e(k+j)满足：

e(k+j)=w(k+j)-y(k+j)。

(10)

式(10)中w(k+j)为系统期望输出。基于上述模型及目标函数推导出的隐式GPC 控制算法仅具有积分结构。将通过改变上述目标函数使得GPC控制算法还具有比例结构。

(11)

其中Kp≥0，Ki≥0是给定常数，分别称为比例因子与积分因子。隐式PIGPC在k+j时刻的输出预测值为：

y(k+j)= GjΔu(k+j-1)+Fjy(k)+

HjΔu(k-1) 。

(12)

记f(k+j)=Fjy(k)+HjΔu(k-1)，则上式可以写为：

y(k+j)=GjΔu(k+j-1)+f(k+j)。

(13)

使用预测值代替实际值，则j步后输出与设定值的偏差及偏差增量可定义如下：

e(k+j)=w(k+j)-f(k+j)-GjΔu(k+j-1)，

(14)

Δe(k+j)=[Δw(k+j)-Δf(k+j)]-[GjΔu(k+j-1)-Gj-1Δu(k+j-2)]。

(15)

将式(14)与式(15)代入目标函数式(11)，并且∂J/∂Δu=0，得到：

(16)

其中

ΔU(k)=RpΔE(k)+RiE(k)。

(17)

则隐式PIGPC的控制量为

U(k)=U(k+1)+RpΔE(k)+RiE(k)。

(18)

为了进一步化简目标函数，定义

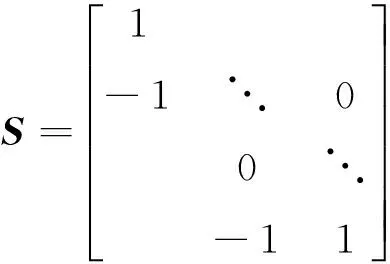
则有Gp=SGi，Δw=Sw，Δf=Sf，代入式(16)有

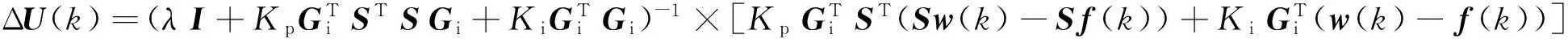
(19)

令Ω=KiI+KpSTS，则有

(20)

式(20)为控制增量的形式，同标准隐式GPC算法相比，并不增加多少计算量，却可以得到更好的控制效果。

2.2 隐式PIGPC算法稳定性分析

利用常用的CARIMA模型描述被控对象[19]：

A(z-1)y(k)=B(z-1)u(k-1)+C(z-1)ξ(k)/Δ。

(21)

式中：y(k)和u(k)分别为系统输出量和控制量；ξ(k)为零均值白噪声序列；q-1为后移算子；Δ=1-q-1为向后一阶差分算子；A(q-1)，B(q-1)与C(q-1)为后移算子的多项式。

对上式用差分算子Δ乘两边后[20]有：

LabVIEW是由美国国家仪器(NI)公司研制开发的，类似于C和BASIC开发环境，它是一种用图标代替文本行创建应用程序的图形化语言编程语言。采用数据流编程方式。

A(q-1)Δy(k)=B(q-1)Δu(k-1)+C(q-1)ξ(k)。

(22)

AY(k)+BU(k)。

(23)

取状态变量为

(24)

则被控对象状态方程[21]可表示为：

X(k+1)=ψX(k)+ΓΔu(k)，

(25)

(26)

由(16)式可得：

Φ″[w(k-1)-FY0(k-1)-

HΔU0(k-1)]。

(27)

这里有：

Y0(k)=[y(k),…,y(k-n)]T，

ΔU0(k)=[Δu(k),…,Δu(k-m)]T，

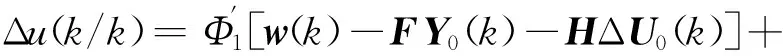
(28)

则在时刻k+1，预测控制队列如下：

⋮

(29)

u(k/k)=u(k-1/k-1)+Δu(k/k)

u(k+1/k)= u(k-1/k-1)+Δu(k/k)+

Δu(k+1/k)

⋮

u(k+N-1/k)= u(k-1/k-1)+Δu(k/k)+

(30)

若在k+1时刻，有n步采样周期时间的延迟发生，则有

Δu(k+n/k+1)= u(k+n/k+1)-

Δu(k+n/k)=

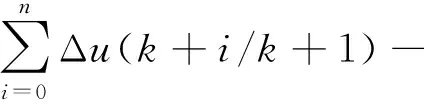
(31)

由式(29)，式(30)及式(31)可得：

HΔU0(k-1)]}。

(32)

结合状态变量，上式转换为

(33)

由式(28)可知

(34)

由于系统的给定不影响系统稳定性分析，因此令w(k-1)，w(k)，w(k+1)为零，则结合式(26)，式(33)，式(34)有

Δu(k+n/k+1)=-LX′(k)。

(35)

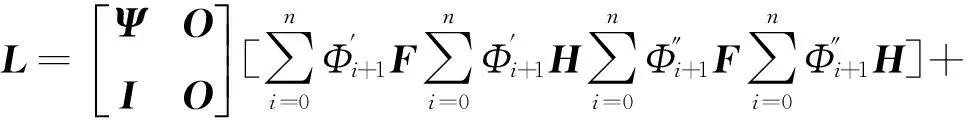
(36)

则式(35)可看作式(26)的状态反馈，闭环系统的状态方程为

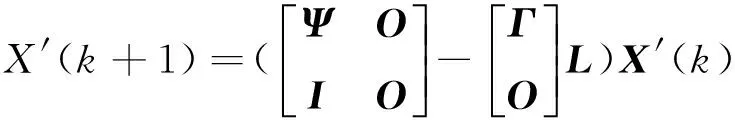
(37)

定理1 在存在随机时延的网络控制系统中，对于任意一个给定正定对称矩阵Q，若有一个正定实对称矩阵P，满足如下方程

-Q。

(38)

则闭环系统(37)是渐近稳定的。

证明 令V(k)=X(k)PX(k)则

ΔV= V(k+1)-V(k)=

XT(k+1)PX(k+1)-

XT(k)PX(k)=-XT(k)QX(k)。

(39)

由Lyapunov稳定性定理可知，若Q为正定，则ΔV为负定的，闭环系统逐渐稳定，证毕。

3 基于隐式PIGPC的时延补偿方法

网络控制系统时延补偿方法具体如下：因为控制器采用隐式PIGPC算法，所以在k时刻可以计算出未来P个周期的控制量序列(P为控制长度)，但是，具体采用控制序列中的哪个控制量作用于执行器，可根据时延和采样周期的关系来确定。

假设系统的采样周期为T，当前控制周期时延为τ。

令

(40)

选择u(k+n|k)作为当前控制量。这样当经过时延τ后，正好在k+n时刻作用于被控对象，将网络时延的控制系统变为无时延的控制系统。

综上所述，可以给出基于隐式PIGPC的网络时延补偿控制器的流程图如图4所示。

图4 网络时延补偿控制器的流程图Fig.4 Flow of network time-delay compensation controller

控制量的具体计算步骤如下所示：

1)在k时刻，使用变步长自适应LMS滤波算法对当前时刻网络时延进行预测，得到当前时刻时延τ(k)，并根据公式(40)求出n；

2)使用公式(20)，通过隐式PIGPC求取控制增量ΔU；

3)根据ΔU求取u(k+n|k)作为当前控制量，并发送到执行器，执行器将控制量作用于被控对象；

4)k+1时刻返回第一步。

4 仿 真

利用True Time搭建一IEEE802.11 b无线网络控制系统，选择无线网络的原因在于相对于有线网络，无线网络时延分布更具随机性，能够验证时延补偿的效果。图5为仿真系统结构图。

图5 仿真系统结构Fig.5 Structure of simulation systems

其中：传感器与执行器为时间驱动；控制器为事件驱动；被控对象为Gp(s)=1/(s2+100s+1)；采样周期T为0.01 s；设置网络速度为80 000 bits/s；最小帧大小80 bits；数据包大小为250 bits；系统中加入干扰节点，干扰比例为10%；系统丢包率设置为5%，干扰与丢包可使网络负载产生变化。首先确定变步长自适应LMS时延预测算法的参数，当系统中存在干扰时，网络时延会在4T之内变化，在仿真系统中采集了300组网络时延数据，前200组用于确定时延预测算法参数，后100组用于预测算法精度的验证。利用网络时延实际值与估计值之间的均方根误差(MSE)作为评价指标，经过大量的实验，确定α=3 000，β=0.2，N=10时算法能快速的收敛同时具有很好的预测效果(对于本文的时延补偿方法，时延估计并不需要特别高的精度，只需要确定当前时刻的时延几倍于采样周期即可)。同时该预测算法预测当前时刻时延只需要0.875 ms，远小于系统采样周期，可以满足实际的应用。图6给出了时延预测算法对于100组测试数据的预测效果。

在确定时延预测算法参数之后，进行基于隐式PIGPC的时延补偿效果的验证，同文献[11]中方法的时延补偿效果进行了对比。隐式PIGPC参数选取预测步长P=6，控制步长M=5，加权系数λ=1，遗忘因子μ=1，柔化系数α=0.1，Kp=0.5，Ki=0.5，文献[11]中的AR阶数p取为10，改进GPC的预测步长P=6，控制步长M=5，加权系数λ=1，输入参考信号为方波。图7为无干扰无丢包、图8为加入干扰但无丢包、图9为干扰与丢包都存在的时延补偿效果。

图6 实际时延与预测时延对比Fig.6 Comparison of actual and prediction time-delay

图7 无干扰无丢包输出跟踪效果对比Fig.7 Output tracking without interference and packet loss

图8 有干扰无丢包输出跟踪效果对比Fig.8 Output tracking with interference and without packet loss

对比算法的网络时延补偿效果，可以发现3种情况下，隐式PIGPC的控制效果都要优于文献[11]的改进GPC算法。同时，对时延补偿方法运行时间进行了计算(CPU为Intel E6550 2.33 GHz, 内存2 GB,Windows 7操作系统, 仿真软件为Matlab 2010b)，测量发现隐式PIGPC执行一个控制周期需要约为1.9 ms，而文献[11]中的方法所需要的时间为5.3 ms。可见隐式PIGPC算法在提高了控制效果的情况下减少了运算时间，更加适合实际应用中网络控制系统的时延补偿。

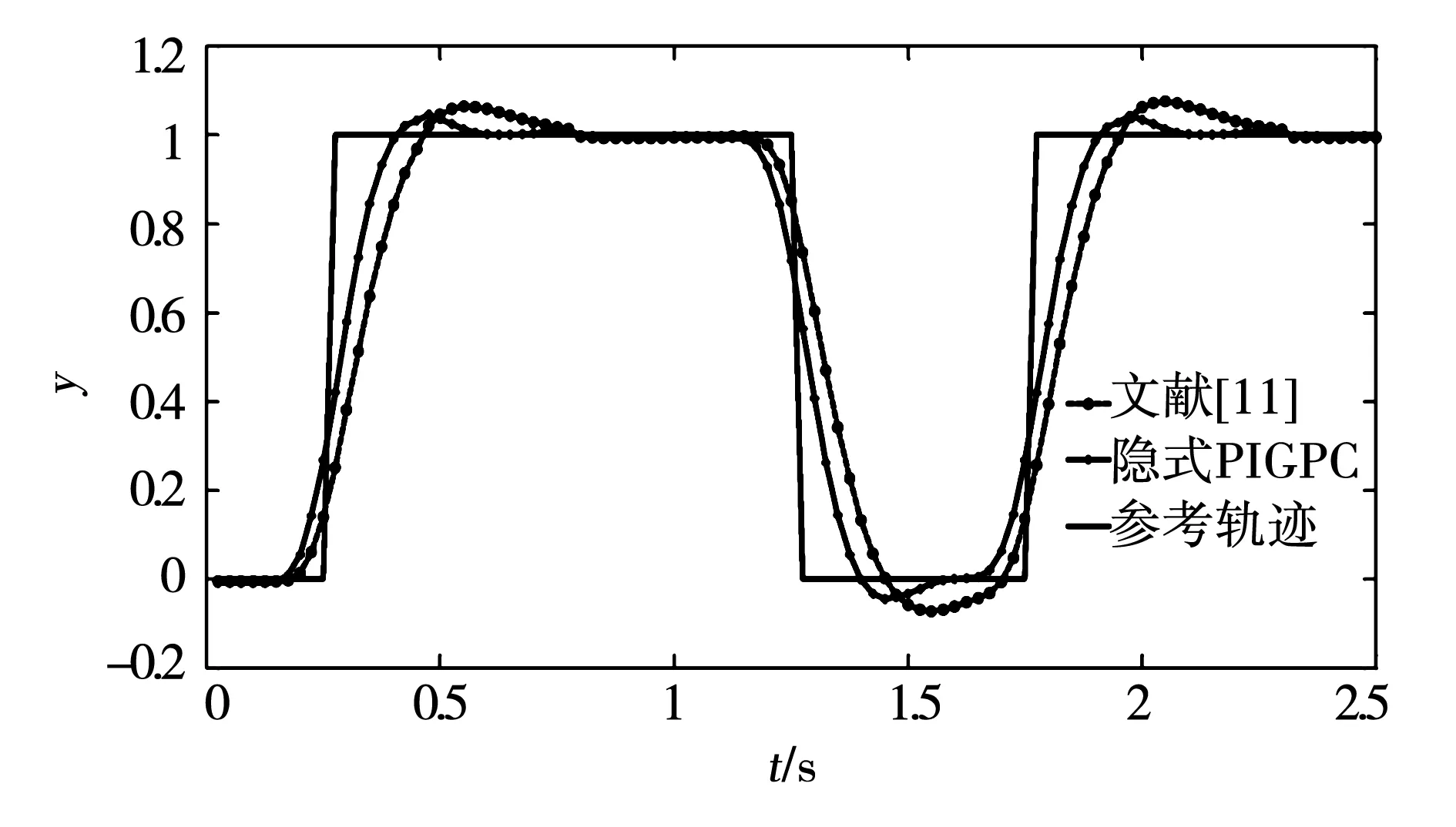
图9 存在干扰与丢包跟踪效果对比Fig.9 Output tracking with interference and packet loss

5 结 论

本文完成了基于隐式PIGPC的时延补偿控制器的设计。由于当前时刻网络时延不可测，为设计控制器，需要对当前时刻的网络时延进行预测，提出一种具有很好预测效果与实时性的变步长自适应LMS滤波算法对当前时刻网络时延进行预测。为改善时延补偿效果，将PI的反馈结构与隐式GPC的预测功能结合起来，提出具有PI结构的隐式GPC算法，结合预测时延对网络时延进行补偿，仿真结果表明隐式PIGPC对网络控制系统时延具有良好的补偿效果，同时算法具有较少的运算时间，更能满足实际应用。

本文仿真中与文献[11]中的改进GPC算法进行了对比，为了进一步验证本文方法的有效性，未来将展开与其他时延补偿方法的对比研究，并继续探讨算法参数对于补偿效果的影响。

[1] LI Weilin, ZHANG Xiaobin, LI Huimin. Co-simulation platforms for co-design of networked control systems: An overview [J]. Control Engineering Practice, 2014,(23): 44-56.

[2] TIAN Zhongda, GAO Xianwen, LI Kun. A hybrid time-delay prediction method for networked control system [J]. International Journal of Automation and Computing, 2014, 11(1): 19-24.

[3] VATANSKI N, GEORGES J P, AUBRUN C, et al. Networked control with delay measurement and estimation [J]. Control Engineering Practice, 2009, 17(2): 231-244.

[4] XU Fengxia, CHENG Yao, REN Hongliang, et al. Research on adaptive neural network control system based on nonlinear U-Model with time-varying delay [J]. Mathematical Problems in Engineering, 2014: 420713.

[5] HAN C W. Fuzzy neural network-based time delay prediction for networked control systems [J]. Applied Mathematics & Information Sciences,2014,8(1):407-413.

[6] QI Xiaomei, ZHANG Chengjin, JASON G. Robust fault detection filter for non-linear state-delay networked control system [J]. International Journal of Automation and Control, 2012, 6(3-4):215-230.

[7] SHI Yang, HUANG Ji, YU Bo. Robust tracking control of networked control systems: application to a networked DC motor [J]. IEEE Transactions on Industrial Electronics, 2013, 60 (12):5864-5874.

[8] 付伟，杨先一，冯伟，等. 网络控制系统时延的预测控制补偿方法[J].系统工程与电子技术,2011,33(9): 2066- 2071.

FU Wei, YANG Xianyi, FENG Wei, et al. Predictive control compensation for time delay in networked control systems[J]. System Engineering and Electronics, 2011,33(9): 2066-2071.

[9] YANG Rongni, LIU Guoping, SHI Peng, et al. Predictive output feedback control for networked control systems [J]. IEEE Transactions on Industrial Electronics, 2014, 61(1): 512-520.

[10] SONG Hongbo, LIU Guoping, YU Li. Networked predictive control of uncertain systems with multiple feedback channels[J]. IEEE Transactions on Industrial Electronics, 2013,60(11): 5228-5238.

[11] 时维国，邵诚，孙正阳. 基于AR模型时延预测的改进GPC网络控制算法[J].控制与决策, 2012,27(3):470-480.

SHI Weiguo, SHAO Cheng, SUN Zhengyang. Improved GPC network-control algorithm based on AR model time-delay prediction[J]. Control and Decision, 2012,27(3): 470-480.

[12] YANG Yanhua, YANG Fangping, HUA Jianning, et al. Generalized predictive control for space teleoperation systems with Long time-varying delays[C]//IEEE International Conference on Systems, Man, and Cybernetics (SMC), Oct 14-17, 2012, Seoul, South Korea. New York:IEEE,2012:3057-3062.

[13] LIU Guoping, XIA Yuanqing, CHEN Jie, et al. Networked predictive control of systems with random network delays in both forward and feedback channels [J]. IEEE Transactions on Industrial Electronics, 2007,54(3):1282-1297.

[14] 安保冉，刘国平. 基于时延补偿机理的网络化输出反馈控制器设计[J]. 物理学报，2014,63(9):090205.

AN Baoran, LIU Guoping. Using time delay compensation scheme in dynamic output feedback controller for networked control systems[J].Acta Physica Sinica,2014,63(9): 090205.

[15] 罗小东，贾振红，王强. 一种新的变步长LMS自适应滤波算法[J]. 电子学报，2006, 34(6): 1123-1126.

LUO Xiaodong, JIA Zhenhong, WANG Qiang. A new variable step size LMS adaptive filtering algorithm[J]. Acta Electronica Sinica, 2006,34(6):1123-1126.

[16] LI Ming, LI Liping, TAI Hengming. Variable step size LMS algorithm based on function control[J]. Circuits, Systems, and Signal Processing,2013,32(6):3121-3130.

[17] GAO Shuzhi, LUAN Liangliang. The PVC stripping process predictive control based on the implicit algorithm [J]. Mathematical Problems in Engineering, 2014: 838404.

[18] 田中大, 高宪文, 李琨. 基于预测控制的NCS时延补偿算法[J]. 系统工程与电子技术, 2013,35(10):2165-2169.

TIAN Zhongda, GAO Xianwen, LI Kun. Networked control system time-delay compensation algorithm based on predictive control[J]. System Engineering and Electronics, 2013,35(10):2165-2169.

[19] 申群太，陈秋凤. 时戳PI广义预测在网络控制系统中的应用[J].控制工程，2009,16(5):538-542.

SHEN Quntai, CHEN Qiufeng. Application of PI Generalized predictive control with time stamp to networked control systems[J].Control Engineering of China, 2009, 16(5): 538-542.

[20] 李韬，陈增强，张纪峰. 比例积分型广义预测控制系统的稳定性分析[J]. 控制理论与应用，2007，24(1)：19-24.

LI Tao, CHEN Zengqiang, ZHANG Jifeng. Stability analysis of systems with proportional-integral generalized predictive control[J]. Control Theory & Applications，2007，24(1):19-24.

[21] ZHANG Jinhui, LAM J, XIA Yuanqing. Output feedback delay compensation control for networked control systems with random delays[J]. Information Sciences, 2014, 265(5):154-166.

(编辑：张 楠)

Implicit PIGPC compensation method for time-delay in networked control system

TIAN Zhong-da， LI Shu-jiang， WANG Yan-hong

(College of Information Science and Engineering, Shenyang University of Technology, Shenyang 110870, China)

A network time-delay compensation method based on implicit PI-based generalized predictive controller (PIGPC)was presented.The variable step size least mean square algorithm was used for time-delay prediction. The predicted time-delay was used instead of the actual time-delay as the parameters of the network time-delay compensation controller. In order to improve the compensation effect of implicit GPC, an implicit generalized predictive control algorithm with PI structure was used to design the controller. Implicit PIGPC doesn′t need to recursive solve Diophantine function and saves online computing time. The feedback structure of PI and the prediction function of GPC were combined to improve the performance of the controller.The time-delay compensation controller was built based on implicit PIGPC and predictive time-delay,and at the same time, the stability of the time-delay compensation algorithm was analyzed.Finally,the simulation results show that the implicit PIGPC has good compensation effect for the time-delay of the networked control system with less computation time.

networked control system; time-delay compensation; time-delay prediction; implicit PIGPC

2014-03-24

国家自然科学基金(61433004)；辽宁省博士科研启动基金(20141070)；辽宁省教育厅科学研究项目(LGD2016009)

田中大(1978—)，男，博士，讲师，研究方向为网络控制系统、混沌时间序列预测；

李树江(1966—)，男，博士，教授，研究方向为复杂工业过程建模与控制；

田中大

10.15938/j.emc.2016.11.011

TP 273

A

1007-449X(2016)11-0077-09

王艳红(1967—)，女，博士，教授，研究方向为生产过程调度与优化控制。