基于三电平斩波器的双电磁铁磁浮系统控制方法

王明义， 曹继伟， 李立毅， 潘东华， 刘家曦

(哈尔滨工业大学 电气工程及自动化学院，黑龙江 哈尔滨 150001)



基于三电平斩波器的双电磁铁磁浮系统控制方法

王明义， 曹继伟， 李立毅， 潘东华， 刘家曦

(哈尔滨工业大学 电气工程及自动化学院，黑龙江 哈尔滨 150001)

在电磁悬浮系统中，由于模型的强非线性，很难实现动子在不同气隙下的稳定悬浮，需要解决系统严重的非线性问题。同时，传统的两电平斩波器驱动方式会带来较大的电流纹波，减小电流控制精度。因此针对单自由度双电磁铁磁浮平台，建立了系统的二阶电流型非线性数学模型，通过三电平控制方法，减小悬浮电流纹波，且升高母线电压后不影响电流精度。结合PID控制器，设计了精确反馈线性化的双电磁铁工作电流切换模式，提出了单自由度磁浮系统全行程悬浮的控制方法。仿真和实验结果表明，在不同悬浮气隙条件下，设计的非线性控制系统能够实现悬浮体的稳定悬浮。

磁悬浮；双电磁铁；三电平；反馈线性化；非线性

0 引 言

磁悬浮技术由于具有无摩擦力、在真空中能够应用和可调的刚度、阻尼和带宽等优点，广泛应用在交通运输、磁轴承和隔振系统中[1-5]。尤其在近年来高档数控机床和光刻机等设备的需求下，磁浮导轨具有广阔的发展前景。由于磁浮导轨兼具磁浮列车高速运动和磁轴承精密悬浮，而上述两种设备中广泛应用吸力型电磁铁悬浮系统，因此由多个电磁铁提供悬浮力的方法是目前磁浮导轨的主要结构形式[6-8]。电磁铁作为磁浮导轨磁浮单元，其本身具有开环不稳定性和模型非线性的问题，加大了控制系统的设计难度[9]。

电磁悬浮系统中电磁力、电流和气隙之间的三维关系复杂，存在严重的非线性，传统的控制策略是通过对悬浮系统在平衡点处进行线性化处理，针对近似的线性化模型进行控制，但这一方法具有一定的局限性，使得悬浮体偏离平衡位置后，控制性能下降，甚至失控[10]。为解决这一问题，文献[11]提出了近似于全局线性化的增益调度方法，该方法通过对若干个平衡点分别进行线性化处理来实现，但为了确保在全行程内获得较高的悬浮性能，需要细分悬浮气隙并将大量信息储存到查找表中，增加了控制系统的计算量。

为了实现全行程稳定悬浮，非线性控制技术应用到磁悬浮控制系统中[12-14]。反馈线性化是一种将系统的非线性模型转换成简单线性模型方法，其思想是通过对系统输出变量的反馈，将原来的非线性系统在全行程范围内精确转换成线性系统，以至于线性控制技术能够应用于非线性系统中。文献[15]、[16]将反馈线性化与鲁棒控制技术结合后应用于电磁悬浮系统中，提出的方法对参数摄动和外部扰动具有较强的鲁棒性；文献[17]、[18]利用反馈线性化得到精确线性化模型，采用状态反馈设计闭环系统控制器，但需要合理的极点配置才能实现良好的控制特性；文献[19]将反馈线性化应用于磁浮开关磁阻电机轴向悬浮力的控制中，并结合PID控制实现精确的悬浮。

由于单电磁铁悬浮系统中悬浮体只受单向吸力，当悬浮气隙小于平衡点气隙时，只能通过自身重力调节，因此控制特性较差，本文设计了双电磁铁单自由度磁浮平台，将双电磁铁非线性模型进行反馈线性化，通过PID控制器输出值调配双电磁铁的工作状态，并结合三电平控制技术减小电流内环的纹波，最后通过仿真和实验，验证了提出的控制方法能够使悬浮体在全行程范围内稳定悬浮。

1 双电磁铁系统模型

由于双电磁铁能够提供悬浮平台双向力，提高系统的刚度和动态响应能力，因此研究的单自由度磁悬浮平台是由双电磁铁构成，如图1(a)所示，电磁铁为E型结构，磁链在铁心、气隙和悬浮平台中形成闭合回路，等效磁路如图1(b)所示。

图1 双电磁铁结构Fig.1 Double-electromagnet structure

磁动势(MMF)为Ni，N为绕组匝数，i为线圈中电流，总磁阻表达式为

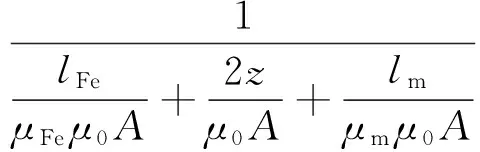
(1)

其中：RFe，Rz，Rm分别为铁心、气隙和悬浮平台对应的磁阻；μ0为真空磁导率，μFe和μm分别为铁心和悬浮平台的相对磁导率；z为悬浮间隙；lFe和lm分别为磁路在铁心和悬浮平台中的平均长度；A为电磁铁等效截面积。此外，磁路的磁通为

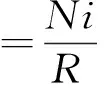
(2)

在线性磁路条件下，电磁铁电感表达为

(3)

其中ψ为磁路磁链。磁场能量为

(4)

通过能量转换原理，有

dWf=idψ-Fdz。

(5)

其中F为悬浮力。由于磁能为磁链ψ和气隙z的函数，因此有

(6)

将式(5)与式(6)对比，由于μFe和μm远大于1，忽略铁心和悬浮平台中的磁阻，由式(4)、式(6)可得

(7)

这里k=(μ0AN2)/4，对于参数一致的双电磁铁构成的悬浮系统，平台在z方向的力学方程为

(8)

(9)

2 系统控制器设计

2.1 三电平斩波器的设计

基于三电平斩波器的电流环控制系统如图2所示，其中功率放大器为H桥形式，由于吸力型电磁铁只有单向电流，因此电路由开关管S1和S2，快恢复二极管D1和D2组成。应用在电磁悬浮系统的功率放大器通常为两电平形式，这会带来较大的电流纹波，降低悬浮系统的控制精度和稳定性，而应用三电平功率放大器不仅能减小电流纹波，而且纹波不随母线电压的升高而增加，适合应用在高精度的磁悬浮系统中[20]。

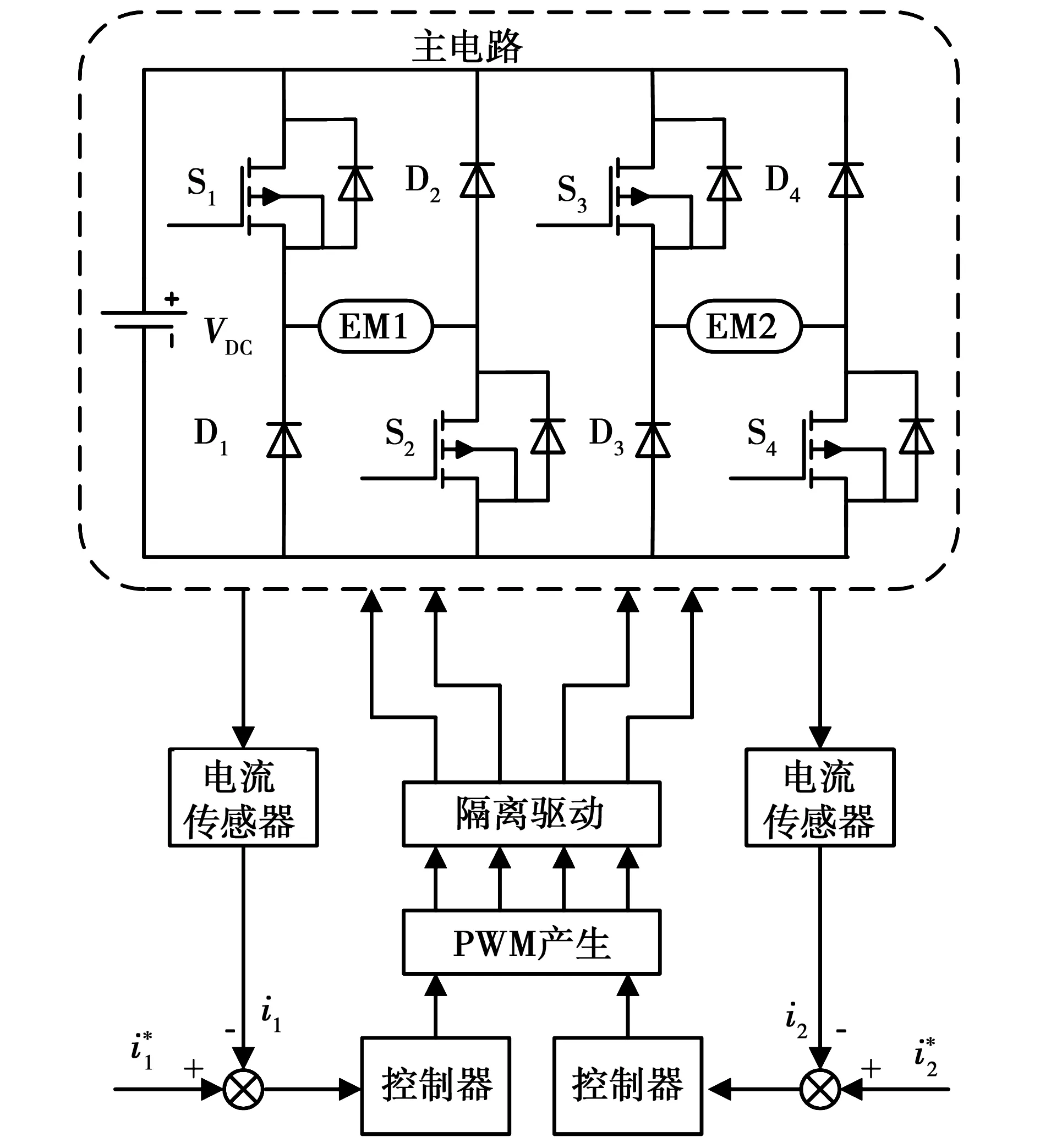
图2 基于三电平斩波器的电流环控制框图Fig.2 Block diagram of current loop based on three-level chopper

开关管的控制信号分别为U1和U2，由调制信号Ug和载波信号Vtri、VtriN比较生成，式(10)为Ug、Vtri和VtriN之间关系如式(11)所示。

(10)

Vtri+VtriN=1。

(11)

式中：Vout为预加到电磁铁上的输出电压；VDC为母线电压。令1代表开通，0代表关断，则U1和U2可以表示为：

(12)

若U1和U2同时为1，电磁铁两端电压为+VDC；若同时为0，电磁铁两端电压为-VDC；若只有一个为1，电磁铁两端电压为0。

2.2 双电磁铁反馈线性化PID控制

图3为设计的非线性控制策略，通过对双电磁铁悬浮系统进行反馈线性化处理，获得精确全局线性化模型，从而可以在非线性系统中应用线性控制技术。

图3 双电磁铁悬浮系统非线性控制图Fig.3 Nonlinear control diagram of double-electromagnet suspension system

根据状态方程式(9)，应用反馈线性化原理，定义：

(13)

其中v为控制器输出，代表作用在平台上悬浮力产生的加速度，式(13)建立了加速度v与悬浮电流i1和i2的关系式。根据式(13)可将式(9)由非线性状态方程转换为线性状态方程，即

(14)

根据给定值与实际值的控制偏差，将偏差的比例、积分和微分通过线性组合的形式构成的PID控制器作为线性控制器，即：

(15)

式中：Kp为比例系数；τi为积分时间常数；τd为微分时间常数。将式(15)代入式(13)中，可以得到两个电磁铁的控制电流，从而将非线性模型线性化。

对于双电磁铁系统，在稳定悬浮情况下，PID调节后输出的v为正值，上电磁铁提供主要悬浮力，当悬浮气隙小于给定值，此时PID调节后输出的v为绝对值较大的负值，于是下电磁铁提供的瞬间吸力快速将平台拉回给定气隙，这种工作模式不仅能够使非线性悬浮系统在全行程内稳定悬浮，还能提高系统刚度。

3 仿真与实验及其结果分析

为了验证设计方法的正确性，通过SIMULINK仿真分析和搭建的实验平台对前面的理论分析进行验证，悬浮系统的主要参数如表1所示。

表1 悬浮系统主要参数

图4为搭建的双电磁铁单自由度磁悬浮平台，采用直线导轨约束其它五自由度，利用高精度激光位移传感器测量悬浮气隙，电磁铁下表面和悬浮平台均经过精磨处理，以高精度浮点型DSP与FPGA结合方案作为控制器的主控芯片。

图4 单自由度磁浮实验平台Fig.4 Single degree of freedom magnetic suspension experimental setup

3.1 三电平斩波器

根据理论分析结果，若电磁铁与悬浮平台间气隙固定，电流环给定为正弦指令，在不同母线电压条件下，分别对两电平和三电平控制技术进行分析。

图5和图6是母线电压分别为20 V和40 V时，两电平控制和三电平控制的仿真结果。从仿真结果可以看出，在相同母线电压下，三电平方案能减小电流纹波，与此同时，随着母线电压的升高，纹波在两电平控制条件下也同时增大，而基于三电平控制的纹波基本不变。由于电流带宽限制，实际电流滞后于指令电流，指令与实际电流间存在略微偏差。

图5 母线电压为20 V的正弦指令跟踪仿真结果Fig.5 Sinusoidal command tracking simulation results when bus voltage is equal to 20 V

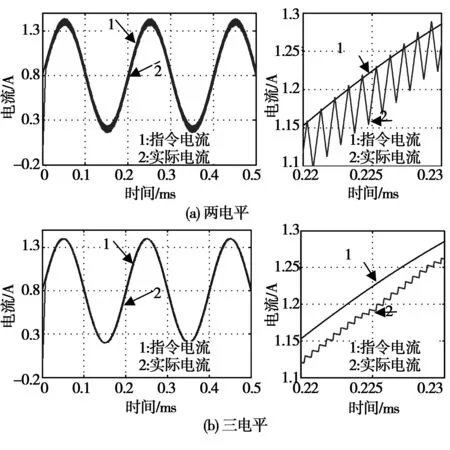
图6 母线电压为40 V的正弦指令跟踪仿真结果Fig.6 Sinusoidal command tracking simulation results when bus voltage is equal to 40 V

图7和图8是母线电压分别为20 V和40 V时，两电平控制和三电平控制的实验结果。可以看出与仿真结果基本一致。因此仿真和实验验证了前面对三电平理论分析的正确性。

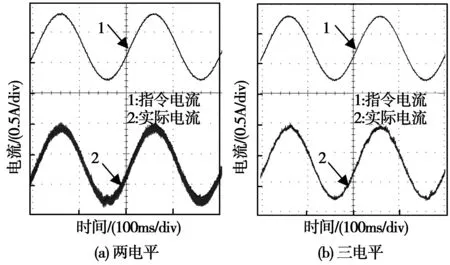
图7 母线电压为20 V的正弦指令跟踪实验结果Fig.7 Sinusoidal command tracking experimental results when bus voltage is equal to 20 V

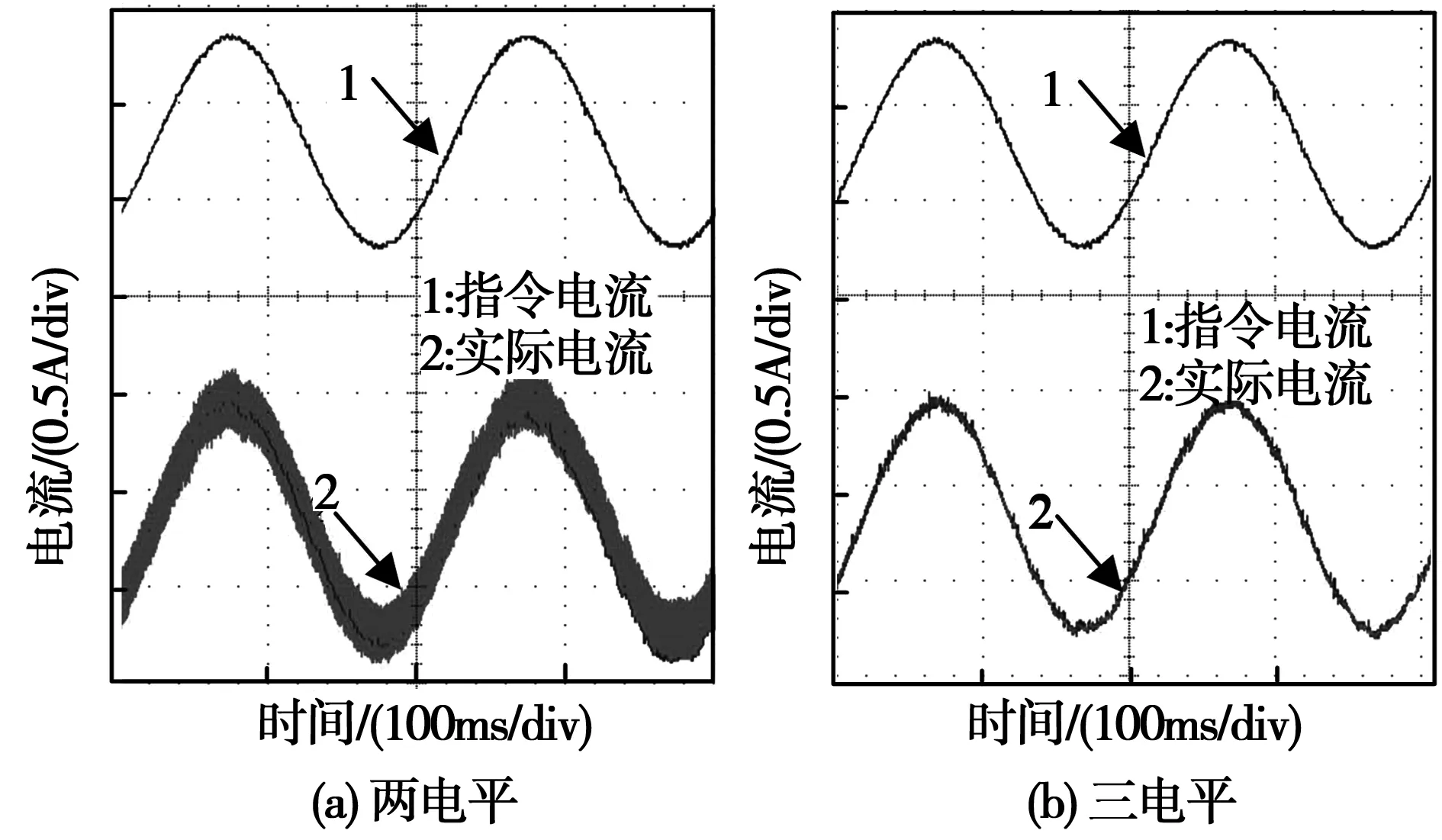
图8 母线电压为40 V的正弦指令跟踪实验结果Fig.8 Sinusoidal command tracking experimental results when bus voltage is equal to 40 V

3.2 双电磁铁方案全行程悬浮

根据设计的双电磁铁反馈线性化控制方法，进行全行程悬浮的仿真和实验。双电磁铁与磁悬浮平台之间的气隙总和为1.8 mm，起始位置为0.2 mm处，悬浮气隙变化步长为0.2 mm。

图9为全行程悬浮的仿真结果，图9(a)为悬浮气隙阶跃变化的跟踪波形，可以看出，悬浮气隙阶跃变化后，经过约60 ms的调整后，悬浮系统达到稳定；图9(b)和图9(c)分别为对应上电磁铁和下电磁铁的工作电流，可以看出在稳定悬浮时，上电磁铁提供悬浮力，下电磁铁仅在悬浮气隙变化时工作，即其提供的瞬间吸力快速将平台拉回给定气隙，验证了理论分析的正确性。

由于搭建的单自由度实验平台以直线导轨约束其它五自由度运动，而在磁浮方向存在一定的非线性摩擦力，对系统的动态特性带来一定影响，因此实验中只对全行程范围内的稳态结果进行分析。图10为全行程悬浮的实验结果，悬浮系统阶跃响应稳定后，将测量的数据存储后绘制波形，图10(a)为稳定后不同悬浮气隙的实验结果，图10(b)为对应的上电磁铁工作电流，结果表明根据设计的控制方法能够实现双电磁铁在全行程范围内稳定悬浮。

图9 全行程悬浮的仿真结果Fig.9 Simulation results of full-stroke suspension

图11为悬浮平台稳定后，上电磁铁的工作电流随气隙变化的仿真与实验结果对比。可以看出，仿真结果的电流与气隙比值接近于常数，与理论值较为接近，而实验中由于不能忽略铁心和悬浮平台磁阻、存在非线性摩擦力等因素，在不同气隙下的工作电流略大于仿真结果，另外，由于两侧导轨存在平行偏差，使得实验与仿真结果的电流偏差逐渐变大。

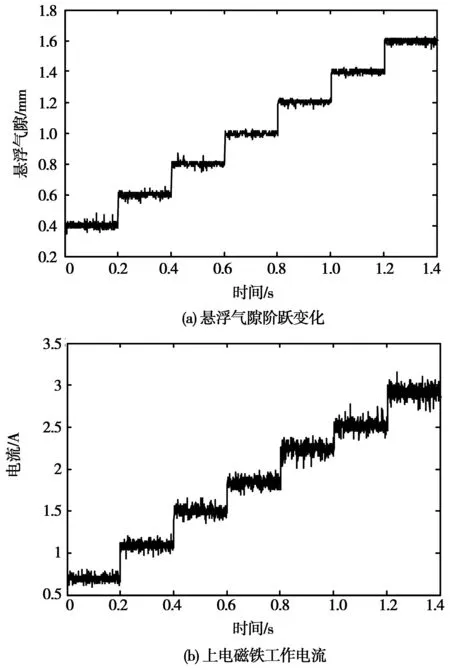
图10 全行程悬浮的实验结果Fig.10 Experimental results of full-stroke suspension

图11 上电磁铁工作电流随气隙变化曲线Fig.11 Variations of up-electromagnet current with airgap length

4 结 论

本文针对电磁悬浮系统中存在的非线性问题进行研究，通过线性PID控制器的输出值确定双电磁铁工作电流切换模式的方法，设计了一种基于三电平控制技术的双电磁铁磁浮系统控制策略，仿真和实验验证了其有效性，并得到如下结论：

1)与两电平斩波器相比，三电平控制方法能够有效降低电流纹波，且纹波不随母线电压的升高而增加。

2)以双电磁铁为模型的反馈线性化方法，可以使非线性的模型全局线性化，最终结合线性控制器能够实现磁浮系统全行程悬浮。

[1] WAI R J，LEE J D．Performance comparisons of model-free control strategies for hybrid magnetic levitation system[J]．IEEE Proceedings-Electric Power Applications，2005，152(6)：1556-1564．

[2] 刘慧娟，张奕黄．磁悬浮列车中直线发电机感应电动势的计算[J]．电机与控制学报，2002，6(3)：191-194．

LIU Huijuan，ZHANG Yihuang．Calculation of electromotive force of linear generator used in magnetic levitation vehicle[J]．Electric Machines and Control，2002，6(3)：191-194．

[3] 张立，刘坤．基于FPGA的飞轮磁轴承一体化控制系统设计[J]．电机与控制学报，2012，16(4)：84-90．

ZHANG Li，LIU Kun．Integrated control system design of magnetic bearings for flywheel based on FPGA[J]．Electric Machines and Control，2012，16(4)：84-90．

[4] CHEN M，KNOSPE C R．Feedback linearization of active magnetic bearings：current-mode implementation[J]．IEEE Transactions on Magnetics，2005，10(6)：632-639．

[5] NAGAYA K，ISHIKAWA M．A noncontact permanent magnet levitation table with electromagnetic control and its vibration isolation method using direct disturbance cancellation combining optimal regulators[J]．IEEE Transactions on Magnetics，1995，31(1)：885-896．

[6] WAI R J，LEE J D，CHANG K L．Real-time PID control strategy for maglev transportation system via particle swarm optimization[J]．IEEE Transactions on Industrial Electronics，2011，58(2)：629-646．

[7] 李奇南，徐德鸿．四电磁铁支撑钢板磁悬浮系统气隙交叉耦合控制[J]．中国电机工程学报，2010，30(33)：129-134．

LI Qinan，XU Dehong．Gap cross-coupling control for 4-Electromagnet supported steel plate magnetic suspension system[J]．Proceedings of the CSEE，2010，30(33)：129-134．

[8] 郭亮，陈本永．精密磁悬浮工作平台的力特性分析[J]．中国电机工程学报，2008，28(21)：118-122．

GUO Liang，CHEN Benyong．A study on force characteristics of precision magnetic levitation stage[J]．Proceedings of the CSEE，2008，28(21)：118-122．

[9] TRUMPER D L，OLSON S M，SUBRAHMANYAN P K．Linearizing control of magnetic suspension systems[J]．IEEE Transactions on Control Systems Technology，1997，5(4)：427-438．

[10] HURLEY W G，HYNES M，WOLFLE W H．PWM control of a magnetic suspension system[J]．IEEE Transactions on Education，2004，47(2)：165-173．

[11] KIM Y C，KIM K H．Gain scheduled control of magnetic suspension system[J]．American Control Conference，1994(3)：3127-3131．

[12] KANELLAKOPOUS I，KOKOTOVIC P V，MORSE A S．Systematic design of adaptive controllers for feedback linearizable systems[J]．IEEE Transactions on Automatic Control，1991，36(11)：1241-1253．

[13] QUEIROZ M S，DAWSON D M．Nonlinear control of active magnetic bearings: a backstepping approach[J]．IEEE Transactions on Control Systems Technology，1996，4(5)：545-552．

[14] KALOUST J，HAM C，SIEHLING J．Nonlinear robust control design for levitation and propulsion of a maglev system[J]．IEEE Proceedings Theory and Applications，2004，151(4)：460-464．

[15] FRANCO A L D，BOURLES H，De PIERI E R．Robust nonlinear control associating robust feedback linearization and H∞control[J]．IEEE Transactions on Automatic Control，2006，51(7)：1200-1207．

[16] DUAN G R，WU Z Y，BINGHAM C．Robust magnetic bearing control using stabilizing dynamical compensators[J]．IEEE Transactions on Industry Applications，2000，36(6)：1654-1660．

[17] 刘德生，李杰，张锟．基于反馈线性化的EMS型磁浮列车非线性悬浮控制器设计[J]．国防科技大学学报，2005，2(27)：96-101．

LIU Desheng，LI Jie，ZHANG Kun．The design of the nonlinear suspension controller for EMS maglev train based on feedback linearization[J]．Journal of National University of Defense Technology，2005，2(27)：96-101．

[18] JOO S J，SEO J H，BINGHAM C．Design and analysis of the nonlinear feedback linearizing control for an electromagnetic suspension system[J]．IEEE Transactions on Control Systems Technology，1997，5(1)：135-144．

[19] 王喜莲，葛宝明，赵楠．磁浮开关磁阻电机悬浮力的反馈线性化PID控制[J]．中国电机工程学报，2009，15(29)：114-118．

WANG Xilian，GE Baoming，ZHAO Nan．Axial suspending feedback linearization PID control for magnetic suspending switched reluctance motor[J]．Proceedings of the CSEE，2009，15(29)：114-118．

[20] 常肖，徐龙祥，董继勇．磁悬浮轴承数字功率放大器[J]．机械工程学报，2010，46(20)：9-14．

CHANG Xiao，XU Longxiang，DONG Jiyong．Digital power amplifier of active magnetic bearing[J]．Journal of Mechanical Engineering，2010，46(20)：9-14．

(编辑：张 楠)

Control method for magnetic suspension system of double-electromagnet based on three-level chopper

WANG Ming-yi， CAO Ji-wei， LI Li-yi， PAN Dong-hua， LIU Jia-xi

(School of Electrical Engineering and Automation, Harbin Institute of Technology, Harbin 150001, China)

In the magnetic suspension system, due to the strong nonlinearity of model, it is difficult to achieve the stable suspension of the mover over the entire operating range,and the nonlinear problem of the system has a significant impact on performance. Meanwhile, the traditional two-level chopper can produce a large current ripple, and decrease the current control precision. For single degree of freedom double-electromagnet system, the nonlinear mathematical model of a second-order current suspension was established; In order to reduce the current ripple,the accuracy of the current was improved through three-level control method; Combined with PID controller, the current switching mode based on the feedback linearization of double-electromagnet system was designed,and nonlinear control strategy for single degree of freedom magnetic suspension system was proposed. Simulation and experimental results show that the proposed nonlinear controller can achieve the stable suspension of the mover under different suspension gap.

magnetic suspension; double-electromagnet; three-level; feedback linearization; nonlinear

2015-03-09

国家自然科学基金 (51537002)；国家科技重大专项(2009ZX02207-001)；国家杰出青年科学基金项目(51225702)

王明义(1986—)，男，博士，讲师，研究方向为直线电机驱动与控制技术；

曹继伟(1983—)，男，博士，讲师，研究方向为新型高速电机的研制设计；

李立毅

10.15938/j.emc.2016.11.010

TP 273

A

1007-449X(2016)11-0070-07

李立毅(1969—)，男，教授，博士生导师，研究方向为特种电机；

潘东华(1982—)，男，博士，助理研究员，研究方向为超精密直线电机系统的研究与应用；

刘家曦(1980—)，男，博士，副教授，研究方向为超精密电机伺服控制、超高速电机驱动控制。