磁悬浮开关磁阻电机多目标优化设计

孙玉坤， 袁野， 黄永红， 胡文宏， 项倩雯， 周云红

(1.南京工程学院 电力工程学院，江苏 南京 210000;2.江苏大学 电气信息工程学院，江苏 镇江 212013)



磁悬浮开关磁阻电机多目标优化设计

孙玉坤1， 袁野2， 黄永红2， 胡文宏2， 项倩雯2， 周云红1

(1.南京工程学院 电力工程学院，江苏 南京 210000;2.江苏大学 电气信息工程学院，江苏 镇江 212013)

研究了一种基于极限学习机(extreme learning machine，ELM)与带精英策略非支配排序遗传算法(improved non-dominated sorting genetic algorithm，NSGA-II)的单绕组磁悬浮开关磁阻电机(single winding bearingless switched reluctance motor，SWBSRM)多目标优化设计方法。结合有限元分析(finite element analysis，FEA)，分析了SWBSRM悬浮力、转矩随各结构参数变化的一般规律，得到ELM非参数模型。针对该训练模型并结合NSGA-II进行全局寻优，获得使悬浮力、转矩同时更优的结构参数数值组合。通过对比优化前后电机输出悬浮力、转矩大小，验证了以ELM、NSGA-II为基础的SWBSRM结构多目标优化设计的有效性。

单绕组磁悬浮开关磁阻电机；多目标优化设计；极限学习机；带精英策略非支配排序遗传算法

0 引 言

随着新能源发电、分布式电源系统、混合动力车辆、航空航天等领域的发展，储能技术已成为世界性的研究课题。众多储能技术中，飞轮电池以功率大、效率高、寿命长、储能密度大、清洁无污染等优点受到国内外的高度重视[1-3]。为减小传统机械轴承摩擦损耗，飞轮电池通常采用多个磁悬浮支承，导致飞轮电池结构复杂、体积庞大。单绕组磁悬浮开关磁阻电机[4-5](single winding bearingless switched reluctance motor ，SWBSRM)集悬浮支承系统与驱动电机于一体，可以作为飞轮电池的核心部件，能很大程度缩短飞轮转子轴向长度，继而提高临界转速、功率密度与系统集成度，进一步减小支承损耗，在高速低损飞轮电池领域具有较高的研究前景与实际应用价值。

现阶段电机优化设计方法以模拟退火、遗传算法、禁忌搜索为代表[6-8]。文献[6]采用的模拟退火算法，具有较好搜索能力，但对整个搜索空间了解不多，采样次数多，优化时间长。文献[7]采用的遗传算法全局搜索能力强，但局部搜索能力较弱。文献[8]采用的禁忌搜索算法可以有效避免寻优过程中大量无效劳动，但条件判断方面不够成熟。

从现有文献来看，对磁悬浮开关磁阻电机[9-10]本体结构优化设计的研究还十分欠缺。文献[9]采用理论分析与有限元仿真相结合的设计方法对双绕组磁悬浮开关磁阻电机结构进行了优化设计，但需要大量的调用计算模型以获得其输出，计算效率低。文献[10]利用支持向量机(support vector machine，SVM)对双绕组磁悬浮开关磁阻电机结构进行模型训练，采用遗传算法进行优化，解决了计算效率低下的问题，但支持向量机在无智能算法进行优化的情况下训练所得模型精度一般，且遗传算法理论仅能实现单一目标最大化寻优，无法同时优化悬浮力与转矩。

本文以12/8 极SWBSRM为对象，在有限数据样本空间的基础上，采用具有高精度、“极端”快速特点的极限学习机[11-14](extreme learning machine，ELM)对数据进行回归训练得到SWBSRM非参数模型，引入带精英策略非支配排序遗传算法[15](improved non-dominated sorting genetic algorithm，NSGA-II)，对训练模型进行参数多目标寻优，获得使悬浮力、转矩同时更优的结构参数数值组合。通过对比优化前后电机输出悬浮力、转矩大小，验证了以ELM、NSGA-II为基础的SWBSRM结构多目标优化设计的有效性。

1 SWBSRM的ELM非参数建模

1.1 SWBSRM电机结构与原理

图1所示为12/8极SWBSRM中的A相绕组配置，每个定子极上绕有一套线圈，逆时针方向依次为A1，A2，A3，A4通过对4个线圈中电流独立控制实现任意方向悬浮力的输出。转矩电流分量ima可产生偏置磁场，该磁场是电机转矩主要来源；x、y方向的悬浮电流分量为isax、isay电流差动励磁可分别产生沿x、y轴方向上的悬浮力分量Fx、Fy，实现转子稳定悬浮。B、C相沿A相绕组逆时针30°和60°放置，悬浮机理与A相完全一致。

1.2 ELM非参数回归建模

ELM是一种简单易用、有效的单隐层前馈神经网络学习算法，由南洋理工大学黄广斌副教授提出。传统的神经网络学习算法需要人为设置大量的网络训练参数，并且很容易产生局部最优解。ELM在算法执行过程中不需要调整网络的输入权值以及隐元的偏置，只需要设置网络的隐层节点个数，即可产生唯一的最优解，具有学习速度快且泛化性能好的优点，因此可以采用ELM训练得到SWBSRM非参数模型。

1.2.1 ELM非线性回归方法

对于N个任意的各不相同的样本，xi=[xi1,…xin]T,yi=[yi1,…yin]T，则一个激励函数为g(x)且具有L个隐含层节点前馈神经网络的输出可以表示为：

(1)

其中，βi=[βi1,…βin]T是连接第i个隐含层节点的输出权值；ai=[ai1,…ain]T是输入层到第i个隐含层节点的输入权值；bi是第i个隐含层节点的偏差；ai·xi表示向量ai与xi的内积。

假如，这个具有L个隐含层节点的前馈神经网络能以零误差逼近这N个样本，则存在ai，bi，βi：

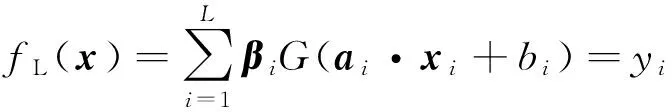
i=1,2,…,L。

(2)

即：

Hβ=Y。

(3)

H为网络的隐含层输出矩阵，则前馈神经网络转化成求解输出权值矩阵的最小二乘解的问题。输出权值矩阵

β=H+Y。

(4)

其中，H+表示隐含层输出矩阵H的Moore-penrose广义逆。

2.2.2 ELM建模的样本空间设计

采用Ansoft/Maxwell 2D 建立12/8极 SWBSRM有限元分析模型，样机主要参数如表1 所示。

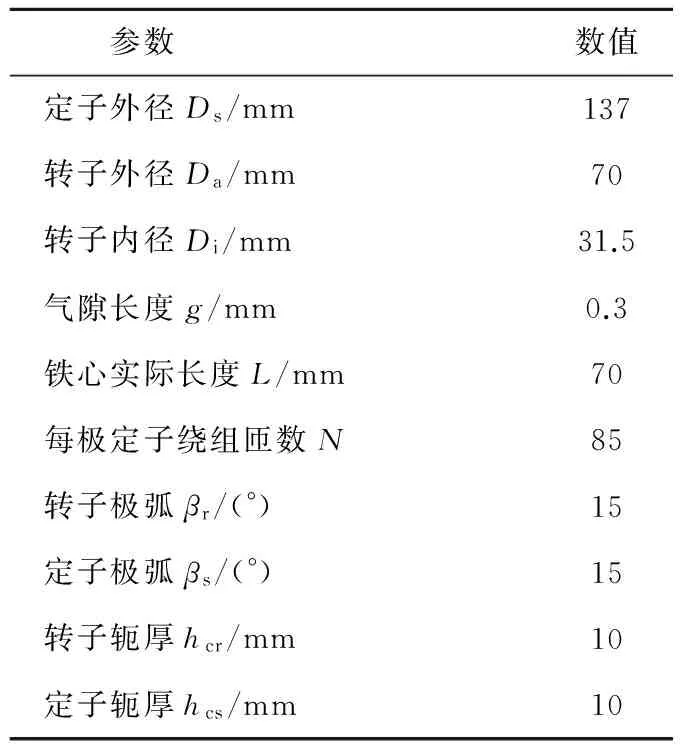
表1 SWBSRM主要参数参数

使用外电路加载直流电压220 V、角度位置控制，可得：相电流有效值约为4.7 A，即有限元仿真中电流转矩分量。通过Matlab/SIMULINK中搭建SWBSRM转子悬浮PID控制系统，得到转子动态偏心时所需悬浮力数值区间为[-20 N～40 N]，则参数优化过程中悬浮电流分量选取最大悬浮力对应的1.88 A，即设置isax=isay=1.88 A。

在电机体积不变，转子无偏心的前提下，依据上述电流大小，可得SWBSRM悬浮力F与各参数关系曲线，分别如图2～图7所示。

图2 悬浮力与转子内径关系曲线Fig.2 Relations between radial force and rotor inner diameter

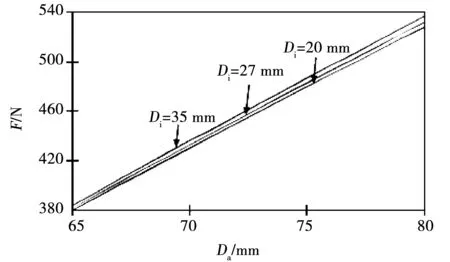
图3 悬浮力与转子外径关系曲线Fig.3 Relation between radial force and rotor outer diameter

图4 悬浮力与转子轭厚关系曲线Fig.4 Relation between radial force and rotor yoke thickness

统一设置A相定子极中心线与转子极中心线成15°夹角，则转矩与各结构参数关系曲线的部分有限元分析结果分别如图8～图13所示。

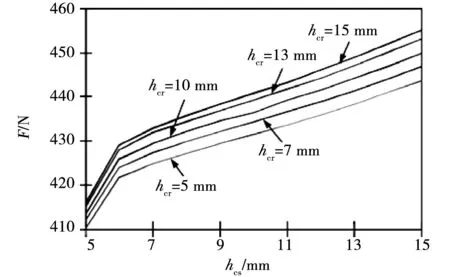
图5 悬浮力与定子轭厚关系曲线Fig.5 Relation between radial force and stator yoke thickness

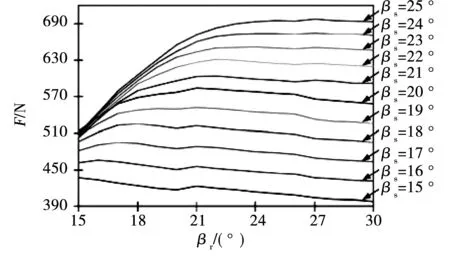
图6 悬浮力与转子极弧关系曲线Fig.6 Relation between radial force and rotor pole arc

图7 悬浮力与定子极弧关系曲线Fig.7 Relation between radial force and stator pole arc

分析图2～图13，可知：

1)悬浮力F随转子内径Di、转子外径Da、定子轭厚hcs、转子轭厚hcr的增加而单调增加。定子极弧βs和转子极弧βr增加，悬浮力先增加后趋于稳定。

图8 转矩与转子内径关系曲线Fig.8 Relation between average torque and rotor inner diameter

图9 转矩与转子外径关系曲线Fig.9 Relation between average torque and rotor outer diameter

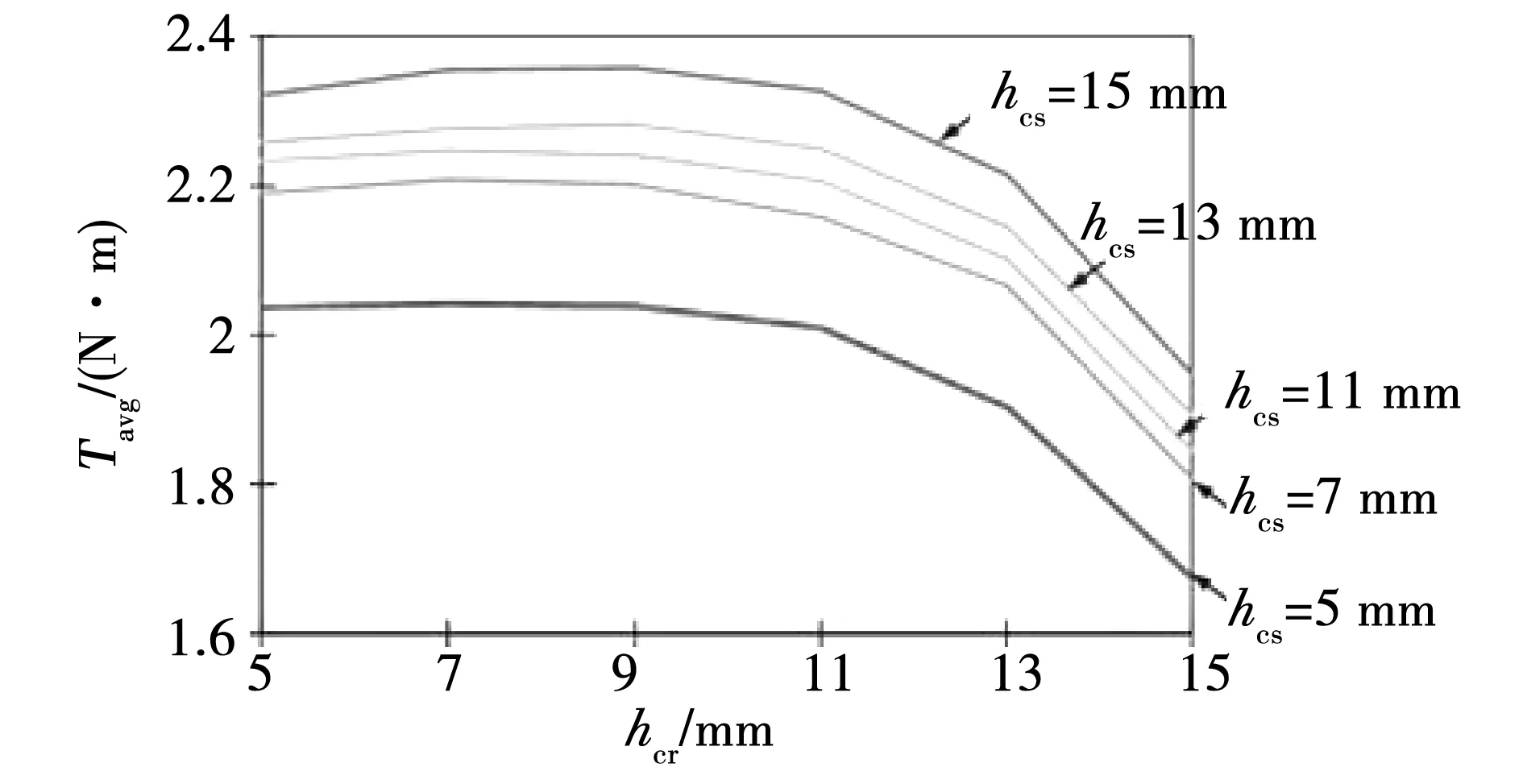
图10 转矩与转子轭厚关系曲线Fig.10 Relation between average torque and rotor yoke thickness

2)转矩随转子外径Da、定子轭厚hcs增加而单调增加。

3)转矩随转子内径Di、转子轭厚hcr增加而减小；转矩随定子极弧βs、转子极弧βr增加，变化趋势是先增加后减小。

当结构参数增加时(如转子外径Da)，悬浮力与转矩均增加，所以为提高悬浮力、转矩输出，可适当增大该结构参数；因此，最终选择转子内径Di、转子轭厚hcr、定子极弧βs、转子极弧βr为SWBSRM结构优化参数。

图11 转矩与定子轭厚关系曲线Fig.11 Relation between average torque and stator yoke thickness

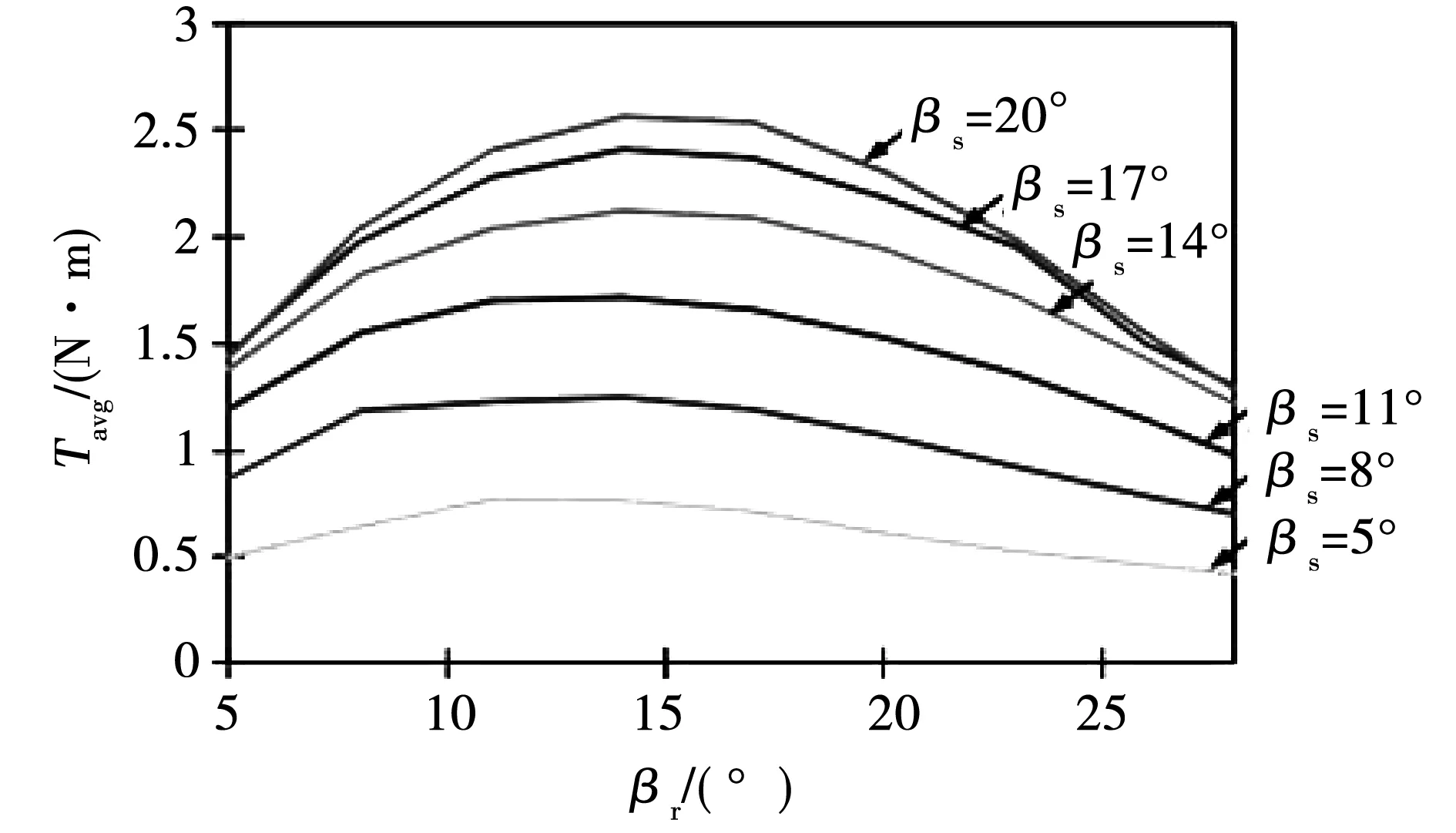
图12 转矩与转子极弧关系曲线Fig.12 Relation between average torque and rotor pole arc

图13 转矩力与定子极弧关系曲线Fig.13 Relation between average torque and stator pole arc

2.3 ELM非线性回归建模精确性验证

在任何转子位置，电机需具有正、反向的自启动能力，电机定子、转子极弧的确定，需要满足以下条件：即

(5)

考虑有限元仿真可行性条件下，βs、βr、Di、hcr的有限元仿真区间分别为[15°, 25°]，[15°, 25°]，[21 mm, 40 mm]和[5 mm, 15 mm]，定步长建立输入为(Di、hcr、βs、βr)、输出为(F，T)的ELM训练样本空间。

根据所得样本数据集，结合ELM可成功实现SWBSRM模型训练。为了验证ELM非参数模型的准确性，以悬浮力F为例，对有限元数据与ELM预测结果进行了对比，具体如图14所示，且图15示出了ELM预测的相对误差绝对值。

图14 FEA、ELM结果对比Fig.14 Comparison between FEM and ELM

图15 ELM模型预测的相对误差Fig.15 Relative errors of ELM prediction

图14中ELM预测结果与有限元数据基本重合，定性地表明了ELM模型具有较高的精确度。图15中显示的ELM模型预测相对误差绝对值大致以0.015为中心线、在0～0.05范围变动，且极少数据点数值大于0.03，可以定量地描述出ELM非参数模型具有很高的精度。

为进一步验证ELM的优越性，将ELM与支持向量机(SVM)模型训练方法进行对比，选取输出量的平均绝对误差绝对值MAD和平均相对误差绝对值MAPE作为评价模型预测效果的性能参数，定义如式(6)、式(7)所示：

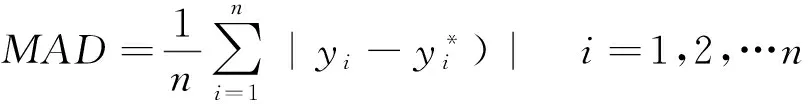
(6)

(7)

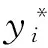
则悬浮力的ELM模型、SVM模型以及FEA模型计算速度、模型精度如表2所示。

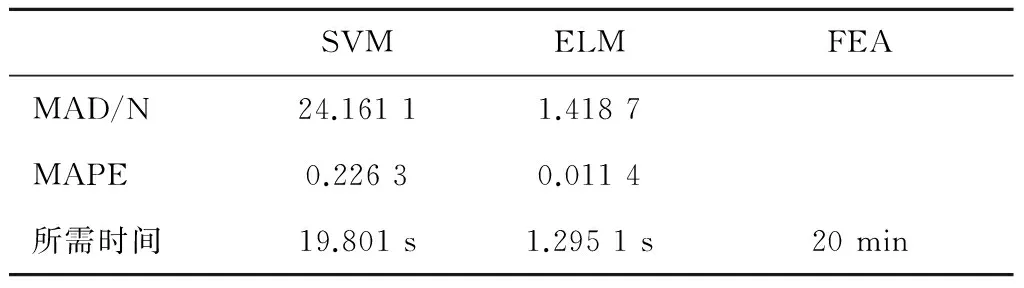
表2 各项性能对比

通过表2可以看出：

1)ELM模型平均绝对误差是SVM模型的5.8%，相对误差是SVM模型的5%。

2)ELM模型计算速度约为SVM模型的15倍，FEA的927倍。

综上，ELM训练所得模型精度高且回归速度快。

3 ELM与NSGA-II多目标优化

鉴于NSGA-II[16-17]在解决多目标优化问题方面具有较高的优越性，首次将NSGA-II应用于SWBSRM本体优化设计[18]的研究中来，具体过程为：NSGA-II全局搜索(Di、hcr、βs、βr)数值组合，使得该数值组合对应的(F，Tavg)同时最大化，而由(Di、hcr、βs、βr)向(F，Tavg)的映射依赖于由ELM训练好的高精度非参数模型。

NSGA-II全局搜索方式与传统GA完全一致，无需赘述；两者区别在于，NSGA-II中任意个体i具备两个属性：非支配序irank和拥挤度id。其中，irank是支配i的个体数目，通过由小到大排序可以将所有个体依次归入F0、F1、F2等集合中，F0集合中个体i对应irank=0，以此类推；id是i周围的个体密度，它可以形象的表示为包含i而不包括其他个体的最大矩形。迭代搜索过程中，可以通过以下准则确定多目标最大化的满意解：当两个个体非支配序不同时，选择非支配序较小值的个体；当两个个体非支配序相同时，选择周围较不拥挤的个体，即选择拥挤度较大值的个体。

在ELM非参数电机模型准确、快速预测的基础上，NSGA-II即可实现SWBSRM结构参数的全局寻优，图16给出了完整的流程图。图16中，当最大代数足够大时(设置最大代数为1 000)，输出的种群所有个体都可以作为非支配序相等的全局满意解，换言之，多目标优化中的满意解是一个集合。

图16 结构优化流程图Fig.16 Flow diagram of optimization design

从全局满意解集中选取两个拥挤度最大的解，作为广义最优解，并与优化之前的电机结构(图17所示)、性能进行对比(表3所示)。分析可知：基于ELM与NSGA-II的SWBSRM结构优化设计使得悬浮力、转矩得到了很大提高，该方法的有效性得到了验证。为了进一步描述优化后SWBSRM悬浮力、转矩的提高，对转子无偏心情况下不同转子位置角下的悬浮力、转矩进行了对比，具体如图18和图19所示，其中，定、转子极中心线对齐位置角为0°，且不同转子角下悬浮力均得到了50～300 N的提高，转矩大小得到了0～2 N·m的提高。因此提出的SWBSRM多目标优化设计方法的有效性得到了很好地验证。

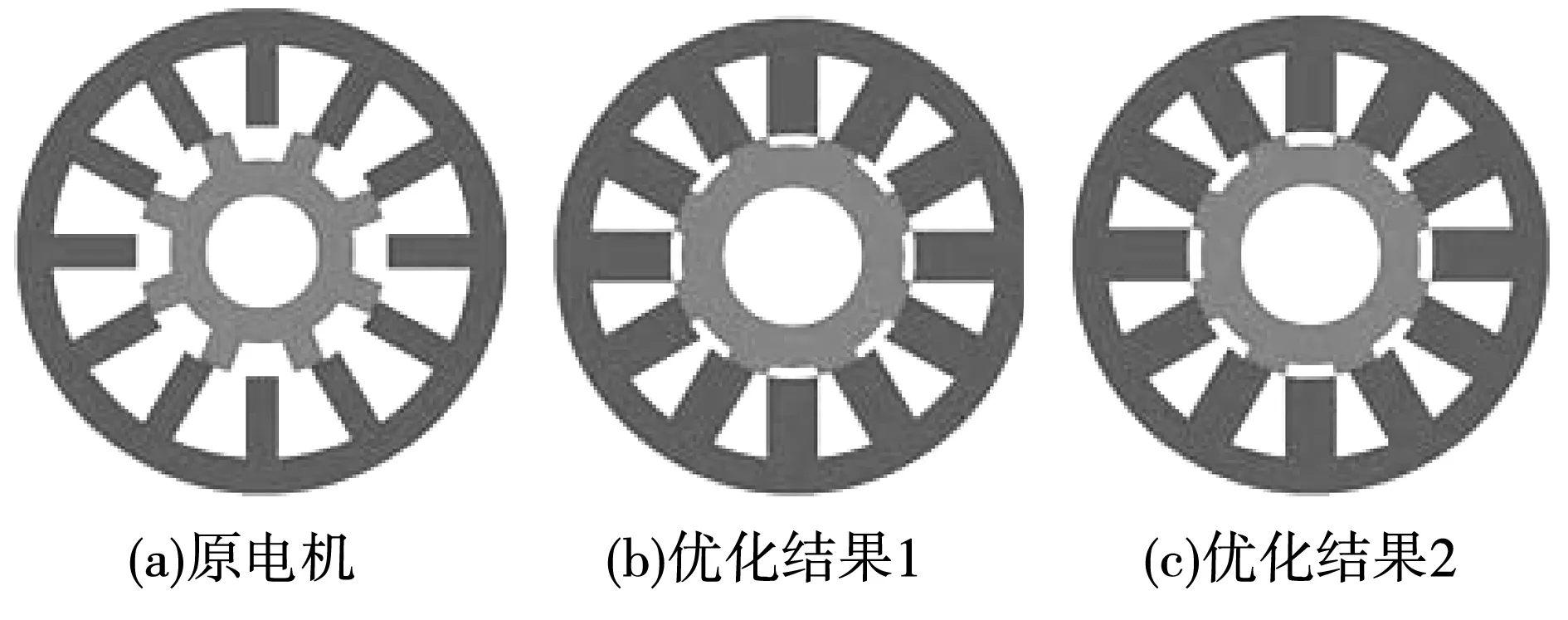
图17 电机截面形状对比Fig.17 Comparison of two cross sections

图18 不同转子位置角下悬浮力对比Fig.18 Comparison of radial forces at different angle positions

图19 不同转子位置角下转矩对比Fig.19 Comparison of torques at different angle positions

参数原电机优化结果1优化结果2βs/(°)1523.423.3βr/(°)1520.520.1Di/mm31.531.540hcr/mm101211.33F/N445.17734.45768.86T/(N·m)2.353.002.94

4 结 论

本文提出了一种磁悬浮开关磁阻电机悬浮力，转矩同时优化的设计方案：通过有限元分析了单绕组磁悬浮开关磁阻电机悬浮力、转矩随各结构参数变化的一般规律，并获得较支持向量机精确度更高的极限学习机非参数模型。针对该训练模型，结合带精英策略非支配排序遗传算法，获得在不同转子位置角下悬浮力、转矩同时更优的电机结构参数数值组合。同时本文采用的多目标优化设计方法也适用于向其他工程应用领域推广。

[1] 张维煜, 朱熀秋.飞轮储能关键技术及其发展现状[J].电工技术学报, 2011,26(7):141-146.

ZHANG Weiyu, ZHU Huangqiu.Key Technologies and development status of flywheel energy storage system[J].Transactions of China Electrotechnical Society, 2011, 26(7): 141-146.

[2] 胡文宏, 孙玉坤, 朱志莹, 等. 基于极限学习机的开关磁阻电机建模[J]. 微电机, 2014, 47(10):10-13.

HU Wenhong, SUN Yukun, ZHU Zhiying, et al.Modeling of switched reluctance motors based on extreme learning machine[J]. Micromotors, 2014, 47(10):10-13.

[3] NGUYEN T, FOO G. Sensorless control of a dual-airgap axial flux permanent magnet machine for flywheel energy storage system[J].IET Electric Power Applications,2013, 7(2):140-149.

[4] 项倩雯, 嵇小辅,孙玉坤. 单绕组磁悬浮开关磁阻电机的原理与解耦控制[J]．电机与控制学报, 2012, 16(11): 22-28．

XIANG Qianwen, JI Xiaofu, SUN Yukun. Principle and decoupling control of single winding bearingless switched reluctance motors[J]. Electric Machines and Control, 2012, 16(11): 22-28．

[5] 项倩雯, 孙玉坤,嵇小辅.单绕组磁悬浮开关磁阻电机无径向位移传感器控制[J]．电工技术学报,2013,28(8):259-267．

XIANG Qianwen, SUN Yukun, JI Xiaofu. Radial displacement sensorless control for single-winding bearingless witched reluctance motors[J]. Transactions of China Electrotechnical Society, 2013,28(8):259-267．

[6] 黄哲理, 赵光, 汪国梁.模拟退火法在电机全局优化设计中的应用研究[J].西安交通大学学报, 1995, 29(2):8-15.

HUANG Zheli, ZHAO Guang, WANG Guoliang. Applied research of the motor global optimization design based on simulated annealing [J].Journal of Xi’an Jiao Tong University, 1995, 29(2): 8-15.

[7] 陈宇,卢琴芬, 叶云岳.长定子同步直线电动机的设计及其优化[J].电工技术学报, 2003,18(2): 18-21.

CHEN Yu,LU Qinfen,YE Yunyue. Optimal design of a long stator synchronous linear motor [J].Transactions of China Electrotechnical Society, 2003, 18 (2): 18-21.

[8] 贾克兵,孙昌治,耿连发.禁忌搜索算法在二相永磁同步电动机中的应用[J].微电机，2002，35(4):18-32.

JIA Kebing, SUN Changzhi, GENG Lianfa.The Application of tabu algorithm to the optimization of two-phase permanent magnet synchronous motor [J]. Micromotors, 2002,35(4):18-32.

[9] 刘羡飞．磁悬浮开关磁阻电机基本参数与控制方法的研究[D]．镇江:江苏大学,2008．

[10] 项倩雯, 孙玉坤, 张新华. 磁悬浮开关磁阻电机建模与参数优化设计[J]. 电机与控制学报,2011,15(4): 74-79.

XIANG Qianwen, SUN Yukun, ZHANG Xinhua. Modeling and parameters optimal design of bearingless switched reluctance motor[J]. Electric Machines and Control, 2011, 15(4): 74-79.

[11] HUANG G B, ZHU Q Y, SIEW C K. Extreme learningmachine: Theory and applications [J]. Neurocomputing, 2006, 70(1/2/3): 489-501.

[12] 顾雪平, 李扬, 吴献吉. 基于局部学习机和细菌群体趋药性算法的电力系统暂态稳定评估[J]. 电工技术学报, 2013, 28(10):271-279.

GU Xueping, LI Yang, WU Xianji. Transient stability assessment of power systems based on local learning machine and bacterial colony chemotaxis algorithm[J]. Transactions of China Electrotechnical Society, 2013, 28(10): 271-279.

[13] 常玉清, 李玉朝, 王福利. 基于极限学习机的生化过程软测量建模[J]. 系统仿真学报, 2008, 19(23): 5587-5590.

CHANG Yuqing, LI Yuchao, WANG Fuli. Soft sensing modeling based on extreme learning machine for biochemical processes[J]. Journal of System Simulation, 2008, 19(23): 5587-5590.

[14] HUANG G B，ZHOU H，DING X，et al．Extreme learning machine for regression and multiclass classification[J]．IEEE Transactions on Systems，Man，and Cybernetics，Part B：Cybernetics，2012，42(2)：513-529．

[15] 冯士刚, 艾芊. 带精英策略的快速非支配排序遗传算法在多目标无功优化中的应用[J]. 电工技术学报, 2008, 22(12): 146-151.

FENG Shigang , AI Qian. Application of fast and elitist non-dominated sorting generic algorithm in multi-objective reactive power optimization[J]. Transactions of China Electrotechnical Society, 2008, 22(12): 146-151.

[16] 肖曦, 许青松, 王雅娉. 基于遗传算法的内埋式永磁同步电机参数辨识方法[J]. 电工技术学报, 2014, 29(3): 21-26.

XIAO Xi, XU Qingsong, WANG Yating. Parameter identification of interior permanent magnet synchronous motors based on genetic algorithm[J]. Transactions of China Electrotechnical Society, 2014, 29(3): 21-26.

[17] 柳高洁, 顾克秋. 结合NSGA-II算法和蒙特卡罗模拟技术实现结构的鲁棒优化[J]. 机械设计, 2009 (4): 65-67.

LIU Gaojie, GU Keqiu. Realizing the robust optimization of structures by combining the NSGA-II algorithm with the Monte Carlo simulation technology [J]. Journal of machine design, 2009 (4): 65-67.

[18] 项倩雯.飞轮电池用五自由度单绕组磁悬浮开关磁阻电机参数设计及运行控[D].镇江：江苏大学，2013.

(编辑：张 楠)

Multi-objective optimal design of single winding bearingless switched reluctance motor

SUN Yu-kun1， YUAN Ye2， HUANG Yong-hong2， HU Wen-hong2，XIANG Qian-wen2， ZHOU Yun-hong1

(1.College of Electrical Engineering, Nanjing Institute of Technology, Nanjing 210000, China; 2.College of Electrical and Information Engineering, Jiangsu University, Zhenjiang 212013, China)

A novel approach was studied using Extreme Learning Machine and Non-dominated Sorting Genetic Algorithm was improved to achieve the multi-objective optimal design of single winding bearingless switched reluctance motor. General rules of radial force and average torque due to the various structure parameters were given based on finite element analyses (FEA), and the ELM non-parametric model of SWBSRM was obtained.The improved Non-dominated Sorting Genetic Algorithm was used to search for optimal solution, by which radial force and average torque were improved simultaneously. The proposed optimal design was verified by comparing the performance of the optimized motors with the original.

single winding bearingless switched reluctance motor; multi-objective optimal design; extreme learning machine; improved non-dominated sorting genetic algorithm

2015-02-10

国家自然科学基金(51377074，51307077)；江苏省优势学科建设工程资助项目；江苏省青年科学自然基金(BK20150510, BK20150524)；江苏大学研究生创新工程项目(KYXX_0002)

孙玉坤(1958—)，男，博士，教授，博士生导师，研究方向为特种电力传动的智能控制；

袁 野(1991—)，男，博士研究生，研究方向为飞轮储能系统优化设计；

袁 野

10.15938/j.emc.2016.11.005

TM 315

A

1007-449X(2016)11-0032-08

黄永红(1970—)，女，教授，博士,研究方向为特种电气传动技术；

胡文宏(1989—)，男，硕士，研究方向为磁悬浮开关磁阻电机参数优化设计及控制技术；

项倩雯(1982—)，女，讲师，博士，研究方向为混合励磁磁悬浮开关磁阻电机设计与控制；

周云红(1982—)，女，副教授，博士，研究方向为特种电力传动及控制研究。