平板表面脊状结构对局部湍流特性的影响研究

王松岭，邓宇涵，吴正人，李子骏，郝晓飞

(华北电力大学 电站设备状态监测与控制教育部重点实验室, 河北 保定 071003)



平板表面脊状结构对局部湍流特性的影响研究

王松岭，邓宇涵，吴正人，李子骏，郝晓飞

(华北电力大学 电站设备状态监测与控制教育部重点实验室, 河北 保定 071003)

利用Fluent软件，通过脊状平板表面数值模拟，分析黏性阻力、压差阻力、壁面切应力、湍流特性等在脊状平板表面中分布规律，基于能量耗散分析，为脊状结构尺寸选取和局部区域改造提供参考依据。结果表明：脊状尺寸越大越有利于黏性阻力减小，但会导致压差阻力增加，而脊状结构压差阻力主要由迎风面与间隔交接处附近高压区决定。高壁面剪切应力集中于相邻沟槽之间区域前段，且脊状结构越小，光滑表面大于脊状结构内壁面剪切应力的区域也相对越多。对脊状结构平板近壁区涡量与湍流特性分析发现，沟槽最底端部分流体是近乎静止的，脊状结构表面涡量与湍流强度均小于光滑表面,而在脊状结构沟槽内所形成的旋涡区域，能量耗散开始大于光滑表面。

脊状结构；数值模拟；分布规律；减阻；优化

0 引 言

脊状结构减阻技术的效果显著并且易于推广，被认为是一种前景广阔的减阻手段，国内外诸多学者对此进行了大量研究。

在国外研究初期，Walsh、Bechert、Choi等对不同形状尺寸纵向布置的脊状结构进行大量研究，初步确立了可以取得减阻无量纲结构尺范围。Choip[1]利用PIV(Particle Image Velocimetry)技术对脊状沟槽表面展向涡结构进行了实验研究，他们认为当脊状结构尺寸与近壁区涡结构尺寸相当时可以取得较好的减阻效果，脊状尺寸相比于涡结构太小则减阻效果不会很好。Ei-Samni 等[2,3]分别利用浸入边界法和有限体积法对流向布置的矩形薄肋沟槽进行了直接数值模拟，通过改变沟槽高与沟槽间距对减阻效果进行研究，得到最大15%的减阻效果。而在国内，刘梅[4]、胡海豹[5]、宋保维[6]等研究非平整表面对流动的影响。吴正人[7]利用文献[8]中阻力计算方法，将脊状结构布置于翼型上进行数值研究，探索其减阻效果。近年诸多学者对传统脊状结构表面进行改造研究。H.T. Wang[9]在脊状结构表面上继续添加微型结构，研究其对流动与传热的影响。郎莎莎[10]对准周期排列的短沟槽减阻机理进行了研究，发现相比与周期性布置的脊状结构，准周期结构可以更好的抑制相干扰动，保持流体条纹的稳定性。刘志华[11]等研究了脊状结构布置位置和来流速度对流动阻力的影响，研究发现来流速度对某种特定的脊状结构的减阻效果影响很大。吴南活[12]对多种脊状结构进行数值模拟研究，探索脊状结构减阻原理，并将不同表面进行结合，探索其减阻原理，得到减阻效果更好的脊状表面。程拼拼[13]对传统V型沟槽和改造后沟槽表面进行了流场对比分析，讨论了在不同雷诺数下，两种沟槽面边界层中壁面切应力、速度分布以及减阻效果。表明优化后沟槽表面更有好的地抑制边界层中湍流流动，减小黏性阻力，取得更好的减阻效果。

目前多数研究为传统对称V型脊状结构或给定改造过后脊状模型，并研究其对流场影响。随着对V型脊状研究的深入，越来越多非传统V型脊状结构开始引起人们的注意。本文对s=0.1 mm、0.2 mm、0.3 mm、0.5 mm、1 mm五种尺寸脊状结构进行数值模拟，依据黏性阻力、压差阻力、壁面切应力、涡结构、湍流特性，研究其在脊状平板表面分布规律，提出基于能量耗散分析的脊状结构尺寸选取和局部改造方法，为设计减阻效果更好的脊状结构提供参考依据。

1 计算模型和数值计算方法

1.1 几何模型和网格划分

本文计算域的左右边界分别距离平板前后端2L,计算域高度为1.5L，如图所示。平板长度为L=200 mm，脊状结构区域的长度为80 mm，布置在整个平板表面的中段，脊状结构选用V型。

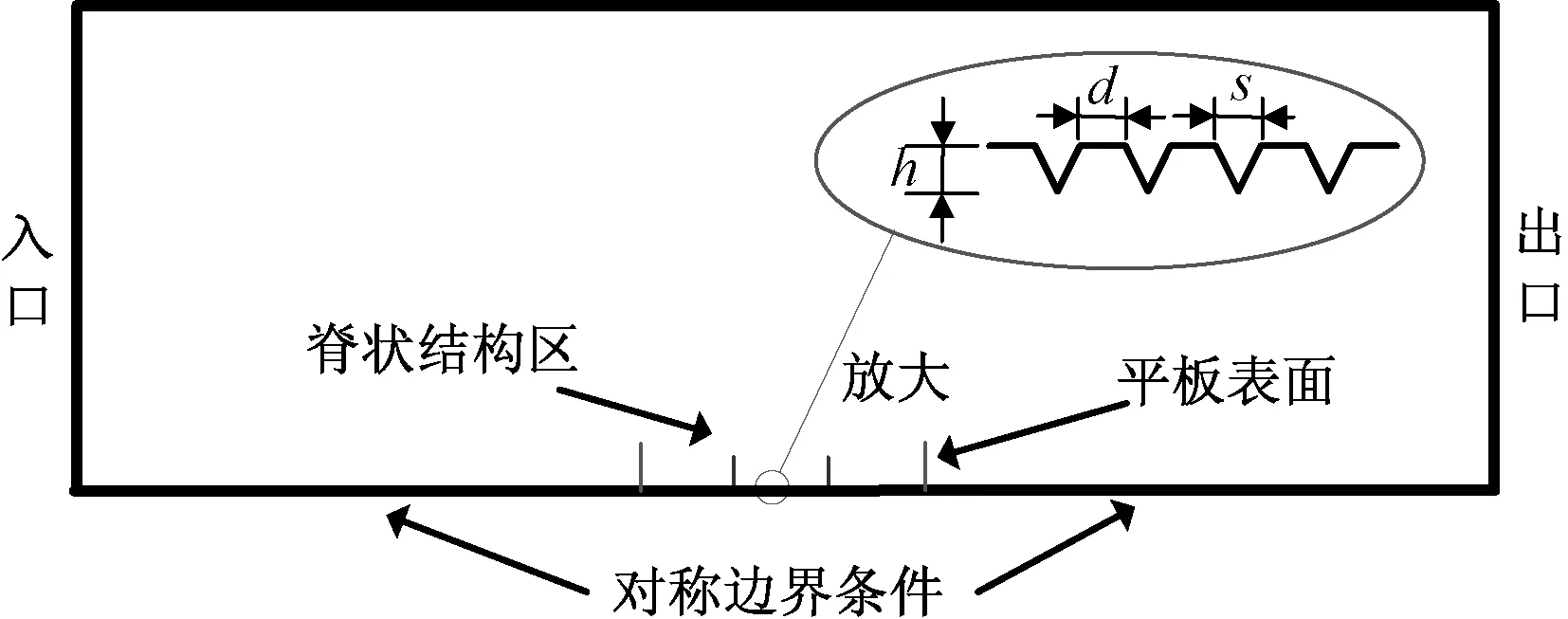
图1 计算域及脊状结构示意图Fig.1 Sketch map of the computational domain and ridge structure

网格的质量和数量是直接影响着模拟结果准确性和可信度。结合模型特点采用非结构化网格，运用尺寸函数进行加密。经计算网格独立性如图2，且壁面y+小于1。

图2 平板表面总阻力随网格数量的变化情况Fig.2 The change of the total drag along with the number of the grid

1.2 控制方程及边界条件

本文湍流模型选用RNGk-ε两方程模型，因为该模型对高应变流动处理较好。选取二阶迎风格式对方程进行离散，速度和压力分离迭代求解采用SIMPLEC算法。

模型入口采用速度入口边界条件，速度方向垂直于入口边界；出口为压力出口，模型上下面为无滑移壁面边界条件，下边界两端采用对称边界条件。

1.3 模拟的准确性验证

为了验证模型选择的准确性及模拟结果的可靠性，对平板模型摩擦阻力系数的理论值及模拟值进行了对比。通过考虑雷诺数大小，壁面摩擦阻力系数经验公式Cf为

如表1所示，模拟值与理论值的相对误差较小，满足计算精度要求。

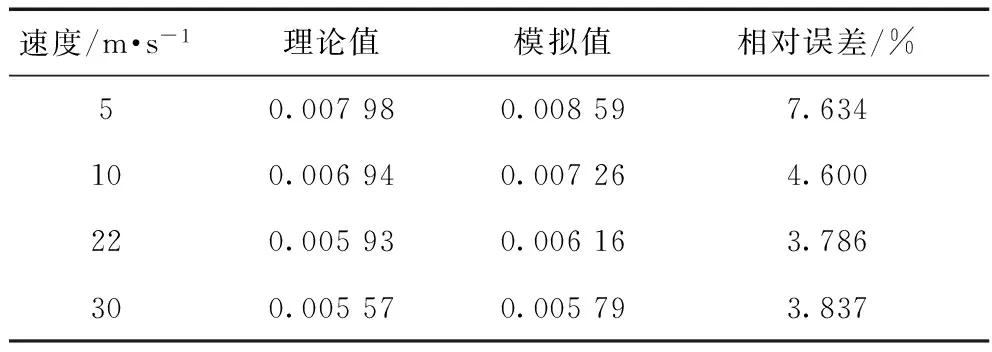
表1 壁面摩擦系数结果比较

2 减阻结果分析

2.1 减阻效果

对s=0.1 mm、0.2 mm、0.3 mm、0.5 mm、1 mm五种尺寸脊状结构进行数值模拟，通过公式计算减阻率

式中：f为光滑面阻力；f1为脊状面阻力。

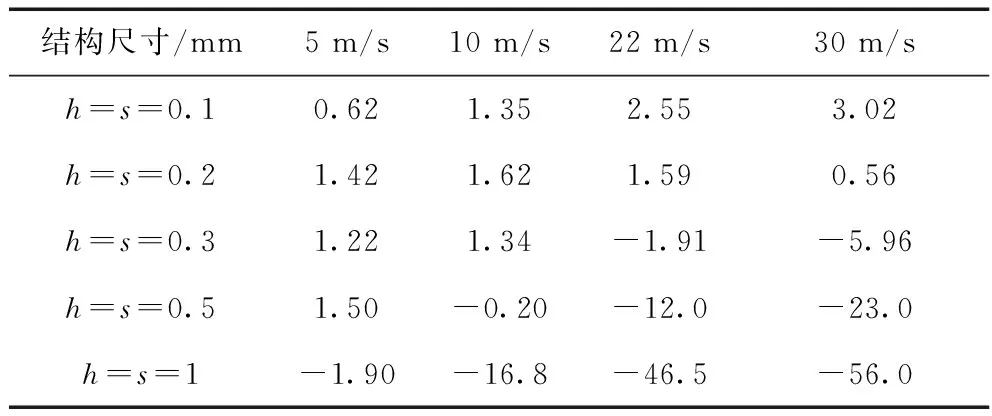
表2 脊状结构减阻率(%)

表2可以明显看出，随着结构尺寸与流速的增大，减阻效果越小，甚至在一定流速或者尺寸时，反而出现增阻现象。

2.2 对局部流动特性影响

空气相对平板面运动,形成边界层，该层近壁区气体微团相对静止，靠该层外侧气体微团则具有流速。因此边界层内存在速度梯度和黏性力，表现为流动阻力。摩擦阻力和压差阻力构成脊状平板总阻力。

研究表明，气体流过脊状表面时，在脊状结构沟槽内部形成了稳定二次涡。如图3，由于脊状结构内部旋涡，气体与壁面接触面减少。在气体与旋涡接触面，二者流向相同，致使黏性阻力减小，导致整体脊状面黏性阻力减少。所以通过增加脊状结构来减少气体与壁面之间直接摩擦，从而减少黏性阻力。但在另一方面，脊状结构的迎风面和背风面上形成压力差，会导致脊状结构平板压差阻力增加。

图3 U=10 m/s，h=s=d=1 mm的流线Fig.3 The streamline of U=10 m/s, h=s=d=1 mm

图4所示，在单个脊状凹槽表面，空气高速流动而在脊状结构迎风面上部区域大量聚集，致使静压力在该区域偏高，而在背风面相对应区域，由于气体不能迅速返回，从而形成一个静压力较低的低压区。由于压差作用，致使高压区与低压区之间气体具有与流动方向相反的流动趋势，表现为压差阻力。因此优化脊状结构迎风面与间隔交接点A附近区域，改善压力差值，可以得到更优的减阻效果。

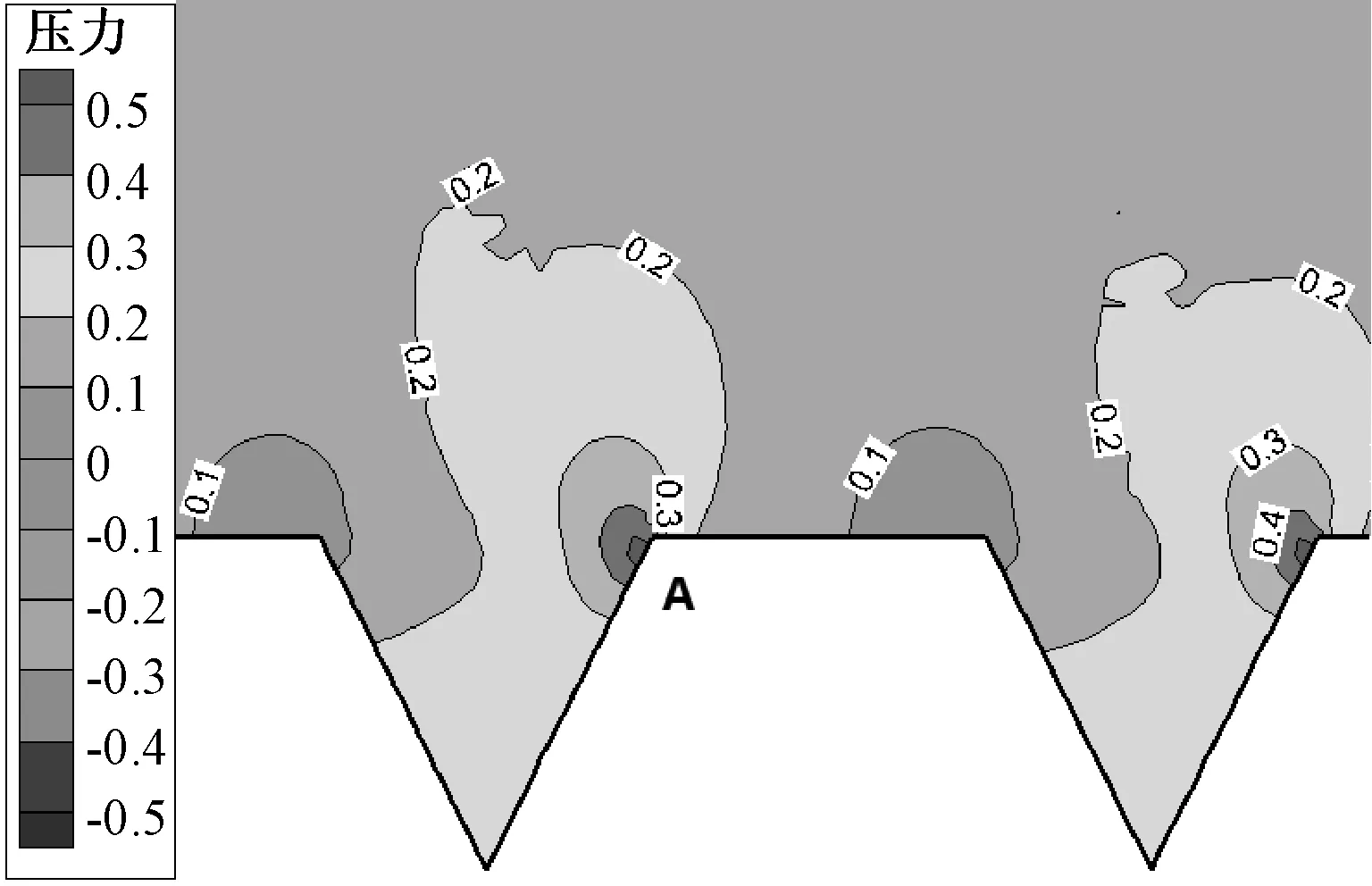
图4 h=s=1 mm的脊状结构静压分布Fig.4 The static pressure distribution of h=s=d=1

图5(a)与图5(b)为间隔尺寸d=0时流速22 m/s和30 m/s条件下不同脊状结构阻力分布情况。如图所示，对于光滑表面，其压差阻力为零，所受黏性阻力即为总阻力。由图可知，脊状结构的压差阻力始终是大于光滑表面的压差阻力的，但随着脊状尺寸减小，高压区与低压区的体积区域减小，致使压差阻力迅速减小。而黏性阻力则由于“滚动轴承”减弱而导致缓慢增加。通过改变脊状结构尺寸，即h=s=d=1和h=s=0.1 mm时进行模拟发现，通过调整脊状结构尺寸来改变压差阻力与粘性阻力，能够取得更优减阻效果。

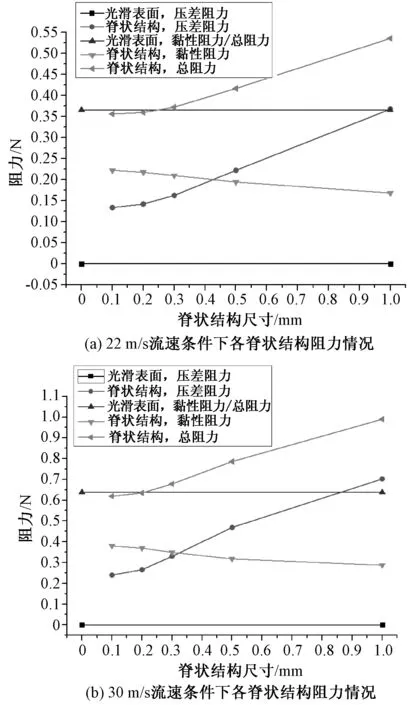
图5 脊状结构平板阻力情况分析Fig.5 Analysis of drag on the plate ridge

壁面摩擦是引起壁面剪切应力主要原因，壁面剪切应力大小反映出模型表面摩擦力大小。由图6中曲线可以明显看出，对于脊状表面模型而言，脊状结构内部表面区域壁面剪切应力相对于光滑表面基本偏低，且随流速增加，脊状表面整体剪切应力均逐渐增大。在相同流速下分析不同脊状尺寸壁面剪切应力发现，越小的脊状尺寸，脊状结构壁面剪切应力大于光滑表面的差值越小，光滑表面大于脊状结构壁面剪切应力的区域也越来越小。相比壁面剪切应力减小区域而言，较小脊状尺寸增加壁面面积非常小，导致整体减阻效果增加。因此，考虑壁面剪切应力在不同尺寸脊状结构表面下分布规律，为合理选择脊状尺寸提供参考。

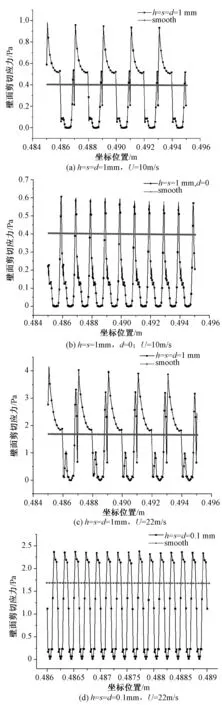
图6 平板模型壁面剪切应力分布曲线Fig.6 The curve of wall shear stress distribution

此外，如图6，高壁面剪切应力集中于相邻沟槽之间区域前段，且逐渐递减。剪切应力低于光滑表面区域，均存在于脊状结构内部表面，而在脊状结构与间隔相连部分壁面剪切应力急速增大。该现象说明表面间隔前段区域壁面剪切应力增大，特别是脊状结构迎风面附近区域。与LAUNDER & LI[14]、数值模拟结果一致。

图7(b)为来流速度22 m/s时，h=s=d=1 mm和h=s=2d=1 mm的两种脊状结构壁面剪切应力对比图。对比两者的壁面剪切应力分布曲线，如图7(b)所示，可以发现，沟槽内部的壁面剪切应力分布几乎没有改变，后者沟槽间隔部分壁面剪切应力变小，而变小壁面剪切应力是由于减少的沟槽间隔，所以适当减少间隔区域有利于减少壁面剪切应力。同时还可以明显看出，沟槽间距的变化，改变了脊状结构的分布周期，而脊状结构壁面剪切应力的分布周期也随分布周期变化而变化。因此，当脊状结构沟槽间隔距离为零时，脊状结构表面的壁面剪切应力取得最小值，这一推测也得到了验证。对脊状结构模型而言，在脊状结构沟槽内底部保留部分几乎静止的流体。这是因为脊谷底部流体流速很低，对壁面作用可以忽略。因此，可以推测，应在脊状结构迎风面与间隔交接点A附近区域进行改造。

图7 22 m/s速度条件下脊状模型壁面剪切应力分布对比Fig.7 Comparison of wall shear stress distribution in the ridge model under the velocity of 22 m/s

由涡量的定义式可知，涡量的大小与流场的速度梯度直接相关，一般来讲速度梯度越大，边界层剪切流场中涡管更容易被拉伸，诱发更多的湍流小涡，产生较大的能量耗散。流动过程中能量耗散伴随涡结构的转化而完成，能量从大涡向小涡传递，小涡向更小的涡传递，此过程伴随着粘性耗散而损失能量。

图8 脊状模型表面法向涡量分布图Fig.8 Normal vorticity distribution of the ridge model

图8为在同一位置处不同流速下光滑表面模型和脊状表面模型涡量在法向方向上分布。在脊状结构沟槽内，涡量很小，随着y值增加，即离开沟槽底部距离越远区域，涡量值迅速增加，且h=s=0.5 mm的脊状结构的涡量是要大于h=s=0.1 mm的脊状结构。这是因为，在沟槽底部，气体几乎静止，如图8所示，在该区域内速度梯度很小，所以产生的涡量较小，而随着y值的增加，逐渐有漩涡产生，速度梯度也迅速增大，涡量也急剧增大。而同一位置高度处，大尺寸的脊状结构的速度梯度是要大于小尺寸的脊状结构的，所以同样位置高度处大尺寸脊状结构涡量会较大。直到开始脱离沟槽后，涡量值才随着y值增加而迅速减小，与平板光滑表面呈现出一样的趋势，但是在壁面近壁区，脊状表面涡量是要小于光滑表面的。在离开边界层区域，三者的流场情况基本一致，因此涡量随y值的变化情况也趋于一致。所以为减少涡量产生，模型优化集中于涡量较大的部分，与前文分析一致。图9为两种来流速度下，光滑表面模型和脊状模型同一流向位置法向湍流参数分布曲线，其中各脊状结构模型所取点均位于V型脊状沟槽的底部端点。由图中曲线可以发现，速度一定的条件下，湍动能和湍流强度的峰值随着脊状结构尺寸的增大而增大，其能量耗散也逐渐增大。由于脊状结构沟槽底端部分几乎静止的流体纯在，脊状结构表面模型湍流耗散小于光滑表面；当到达脊状结构沟槽内所形成的旋涡区域，脊状表面模型的湍动能和湍流强度开始大于光滑表面，且脊状结构尺寸越大，湍动能和湍流强度的相对增幅也越大。湍流强度是评判能量耗散的重要依据，通过以上分析可以发现，能量耗散主要集中于脊状沟槽上部与脱离沟槽的近壁面，因此为减小能量耗散，优化脊状结构的重点集中于脊状结构上部。

图9 平板模型湍流参数分布曲线Fig.9 The curve of turbulent parameters in the plate model

3 结 论

目前多数研究为传统对称V型脊状结构或给定改造过后脊状模型，并研究其对流场影响。随着对V型脊状研究的深入，越来越多非传统V型脊状结构开始引起人们的注意。本文通过数值模拟，对脊状结构表面进行分析，重点对脊状结构中黏性阻力、压差阻力、壁面剪切应力和湍流参数等在脊状壁面分布规律，为脊状结构尺寸选取与局部改造提供参考依据。得到以下结论：

(1)确定脊状结构情况下，黏性阻力减少主要来源于二次涡减少气体与壁面的接触，但与此同时，压差阻力伴随脊状结构尺寸的增加而增加。在单个脊状结构压差阻力主要集中于迎风面与间隔交接处。因此，可为实际中脊状尺寸选取与局部改造区域提供参考。

(2)脊状结构越小，脊状结构表面剪切应力大于光滑表面的差值越小，光滑表面大于脊状结构壁面剪切应力区域也相对越多。高壁面剪切应力集中于相邻沟槽之间区域前段。该现象说明，合理选择脊状尺寸和减少该区域壁面剪切应力有利于取得更好的减阻效果。

(3)由于脊状结构沟槽底端部分几乎静止的流体纯在，脊状结构表面模型能量耗散均是小于光滑表面；而随着离开壁面距离增加，到达脊状结构沟槽内所形成的旋涡区域，脊状表面模型能量耗散大于光滑表面。所以，脊状结构优化应着重考虑脊状结构上部能量耗散较大区域。

[1] CHOI Y S. Decrement of spanwise vortices by a drag-reducing riblet surface[J]. Journal of Turbulence, 2008, 9(23):1-15.

[2] EI-SAMNI O A, YOON H S, CHUN H H. Turbulent flow over thin rectangular riblets[J]. Journal of Mechanical Science and Technology, 2005, 19(9): 1801-1810.

[3] EI-SAMNI O A, CHUN H H, YOON H S. Drag reduction of turbulent flow over thin rectangular riblets[J]. International Journal of Engineering Science, 2007, 45(2-8):436-454.

[4] 刘梅, 刘玉梅, 王松岭. 非平整加热斜面上液膜流动稳定性研究[J]. 华北电力大学学报, 2013, 40(5):108-112.

[5] 胡海豹, 宋保维, 潘光,等. 鲨鱼沟槽表皮减阻机理的仿真研究[J]. 系统仿真学报, 2007, 19(21):4901-49 03.

[6] 宋保维, 刘占一, 胡海豹,等. 翼型表面脊状结构减阻特性的数值仿真研究[J]. 计算力学学报, 2010, 27(5):913-918.

[7] 吴正人, 郝晓飞, 戎瑞,等. 脊状表面翼型叶片减阻机理研究[J]. 系统仿真学报, 2014, 26(6):1355-1361.

[8] 李国光, 王松岭, 仝卫国,等. 基于管道沿程阻力的流量测量方法[J]. 华北电力大学学报, 2000，27(1): 42-45.

[9] WANG H T, LEE W B, CHAN J, et al. Numerical and experimental analysis of heat transfer in turbulent flow channels with two-dimensional ribs[J]. Applied Thermal Engineering, 2015, 75:623-634.

[10] 郎莎莎, 耿兴国, 臧渡洋. 八重准周期排列的短沟槽结构减阻机理分析[J]. 物理学报, 2014, 63(8):244 -254.

[11] 刘志华, 董文才, 熊鹰. 雷诺数对沟槽减阻特性影响的数值分析[J]. 海军工程大学学报, 2007, 19(2): 6-11.

[12] 吴南活. 基于大涡模拟的非光滑表面湍流阻力特性研究[D].广州：华南理工大学，2012.

[13] 程拼拼, 蒋成刚, 吴承伟. 仿生二级微沟槽表面减阻特性数值模拟[J]. 中国科技论文, 2014，(8): 940 -943.

[14] LAUNDER B E, LI S P. On the prediction of riblet performance with engineering turbulence models[J]. Applied Scientific Research, 1993, 19(50):283-298.

Study on Influence of Riblet Structure of Flat Surface on Local Turbulence Characteristics

WANG Songling， DENG Yuhan，WU Zhengren， LI Zijun，HAO Xiaofei

(Key Laboratory of Condition Monitoring and Control for Power Plant Equipment, North China Electric Power University, Baoding 071003, China)

This paper analyzes the distribution law of viscous resistance, pressure difference resistance, wall shear stress and turbulence characteristics on the riblet flat surface by using Fluent to make numerical simulation of the riblet flat surface. The energy dissipation is analyzed and

for size selection and local transformation of riblet structure is provided. Results show that a greater riblet structure will lead to smaller viscous resistance and larger pressure difference resistance; however, the pressure difference resistance of riblet structure mainly depends on the windward side and high pressure area near the junction. The biggest wall shear stress lies in the front interval area of the riblet structure, and it is higher than that of a smooth surface model at the same place. Inside the ridge structure, most wall shear stress is lower than that of a smooth surface. The smaller ridge structure will lead to a smaller area where the wall shear stress inside the ridge structure is smaller than that of the smooth surface. By the analysis of vorticity and turbulent characteristics in the near wall region, the paper finds that the fluid in the bottom of the groove is nearly stationary, the surface vorticity and turbulence intensity of the riblet structure are smaller than that of the smooth surface, and in the vortex area within the groove riblet structure, energy dissipation is greater than that of the smooth surface.

riblet structure; numerical simulation; distribution law; drag reduction; optimization

10.3969/j.ISSN.1007-2691.2016.05.11

2016-01-13.

高等学校博士学科点专项科研基金资助项目(20110036110009)；中央高校基本科研业务费专项资金资助项目(2015MS111) .

TH4；O355

A

1007-2691(2016)05-0068-07

王松岭(1954-)，男，博士生导师，研究方向为热力设备及大型回转机械安全及经济运行、流体动力学理论及应用。