含活性剂液滴铺展过程中的指进特征

叶学民，王媛媛，李春曦

(电站设备状态监测与控制教育部重点实验室，华北电力大学，河北 保定 071003)



含活性剂液滴铺展过程中的指进特征

叶学民，王媛媛，李春曦

(电站设备状态监测与控制教育部重点实验室，华北电力大学，河北 保定 071003)

含活性剂液滴放置在预置液膜上或固体壁面上时，表面活性剂浓度梯度将驱动液滴向周围铺展，并在铺展前沿处呈现出复杂的指进现象。通过数值模拟重现了含不溶性活性剂液滴在预置液膜表面铺展过程中的指进现象，分析了指进现象中不同手指的指长和指宽的增长率，结合液膜厚度的功率谱图，给出了导致液滴铺展最不稳定的最危险扰动波数。研究表明：因初始扰动的存在，在液滴底部的液膜最薄区域产生指进现象，且随时间延续，手指不断伸长、变宽、分叉，指进现象更加显著；施加不同形式的初始扰动呈现的指进现象有所区别：施加余弦扰动下的指进现象中长短手指分布较匀称，而施加随机扰动下的指进现象中长短手指分布均匀性较差，呈随机特征；在当前计算参数情形下，影响液滴铺展稳定性的最危险扰动波数为k=10。

活性剂液滴；铺展；指进现象；功率谱

0 引 言

含活性剂液滴在固体表面上的润湿或去润湿过程在能源、化工、电子和医学等领域具有广泛的应用和潜在的应用前景[1-3]。实验表明，润湿过程中，在液膜前沿处伴有大量的分岔，合并和尖端分裂等复杂的非线性特征，总体上呈手指状，因此称为指进现象[2-7]。同时，理论研究不仅给出了指进现象在空间和时间上的复杂演化特征，而且指出其演化特征还与其初始和边界条件密切联系[2-3]。因此，含活性剂液滴铺展过程中的稳定性及指进特征成为近年来的研究热点。

指进现象的发现及研究源于石油开采领域油水驱替过程中驱替前缘“指状”推进的现象[8]。研究表明指进现象的诱发主要原因是粘性、毛细力、密度、重力等因素，涉及的研究方法既有基于连续介质理论的模拟[9]，也有基于粒子动力学的格子-玻尔兹曼方法(LBM)[10]。与含活性剂液滴铺展过程中的指进现象相比，油水驱替过程的指进现象虽然产生机理不同，但其研究方法具有重要的参考意义。

指进现象的开创性研究始于Marmur和Lelah[7]在1981年的实验结果，其首先描述了含活性剂液滴在玻璃上的前沿枝状分叉特征。之后，陆续开展了许多相关研究。已明确的是活性剂的种类、溶解性、浓度及预置液膜厚度等均对指进现象产生不同程度的影响[2-7]。另一方面，还有许多研究者通过理论建模和数值模拟来重现液滴铺展过程，并基于非模态理论分析了铺展稳定性[2, 11-15]。英国帝国理工学院Matar和Craster领导的课题组于2004-2006年间，通过数值模拟开展指进现象的研究，先后成功再现了含不溶性[12, 15]、可溶性[13]、超过临界胶束浓度[14]的活性剂液滴在平面和倾斜面上[15]的指进现象。但受当时计算机的限制，一次指进现象的模拟计算一般耗时数十天[16]，因此仅分析了初始活性剂浓度和预置液膜厚度对指进特征的影响，而有关指进现象的定量研究，如指进现象中长短手指的指长与指宽等特征量的变化细节，尚未开展。

目前，计算机软硬件飞速发展，根据摩尔定律，计算能力较十年前有数十倍乃至上百倍的提高[16]，使得采用数值方法模拟三维指进现象及其细节特征成为可能。本文所在课题组已经对含活性剂液滴的铺展过程及稳定性开展了大量的建模和数值模拟工作[17-19]。在此基础上，本文通过数值模拟再现上述过程中指进现象的形成过程，比较指进现象中手指长度与宽度随时间的变化率，并通过液膜厚度的功率谱分析探索指进现象的频率特性，获得导致铺展过程最不稳定的扰动波数。

1 理论模型及控制方程

1.1 理论模型

如图1所示，含不溶性活性剂的液滴放置厚度为Hb*的预置液膜上，液滴在活性剂浓度梯度形成的Marangoni效应下向周围铺展，形成如图1所示的外形特征，其中液滴底部厚度因快速减小而形成了超薄液膜区(对应铺展半径Rs)，而在液膜与预置液膜交界处衍生出铺展前沿(对应铺展前沿Xf图1)。铺展中，初始最大厚度H*和流动方向尺度L*的数量级分别为10-5m和10-3m，即H*《L*(上标“*”代表有量纲量)，因此适用润滑理论[20-23]。

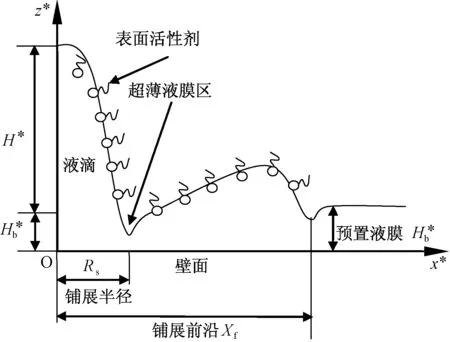
图1 含活性剂液滴的铺展历程Fig.1 Spreading of droplet with surfactants

1.2 控制方程

由描述流体质量、动量和活性剂浓度的输运方程出发，根据润滑理论对控制方程进行无量纲化可得

ux+vz=0

(1)

uzz=px

(2)

pz=0

(3)

(4)

表面张力关系式

无量纲形式的边界条件为

z=0，u=v=0

(6)

z=h，uz=σx

(7)

z=h，p=-Chxx

(8)

z=h，ht+ushx=vs

(9)

综合式(1)～式(9)，采用积分法可推导出液膜厚度和活性剂浓度演化方程式(10)和式(11)。推导过程详见文献[12，17]：

ht=-

(10)

(11)

文中初始液滴的外形和初始活性剂浓度分布分别为

h0(x,y,0)=(1-x2+Hb)H(1-x)+HbH(1-x)+

(12)

Γ0(x,y,0)=ΓcH(1-x)

(13)

图2 初始时的液滴外形和活性剂浓度Fig.2 Initial conditions of the film thickness and surfactant concentration

计算中的边界条件为

hx(∞,t)=hxxx(∞,t)=0

(14)

Γx(∞,t)=0

(15)

铺展中活性剂浓度总量保持恒定：

2 数值模拟结果及分析

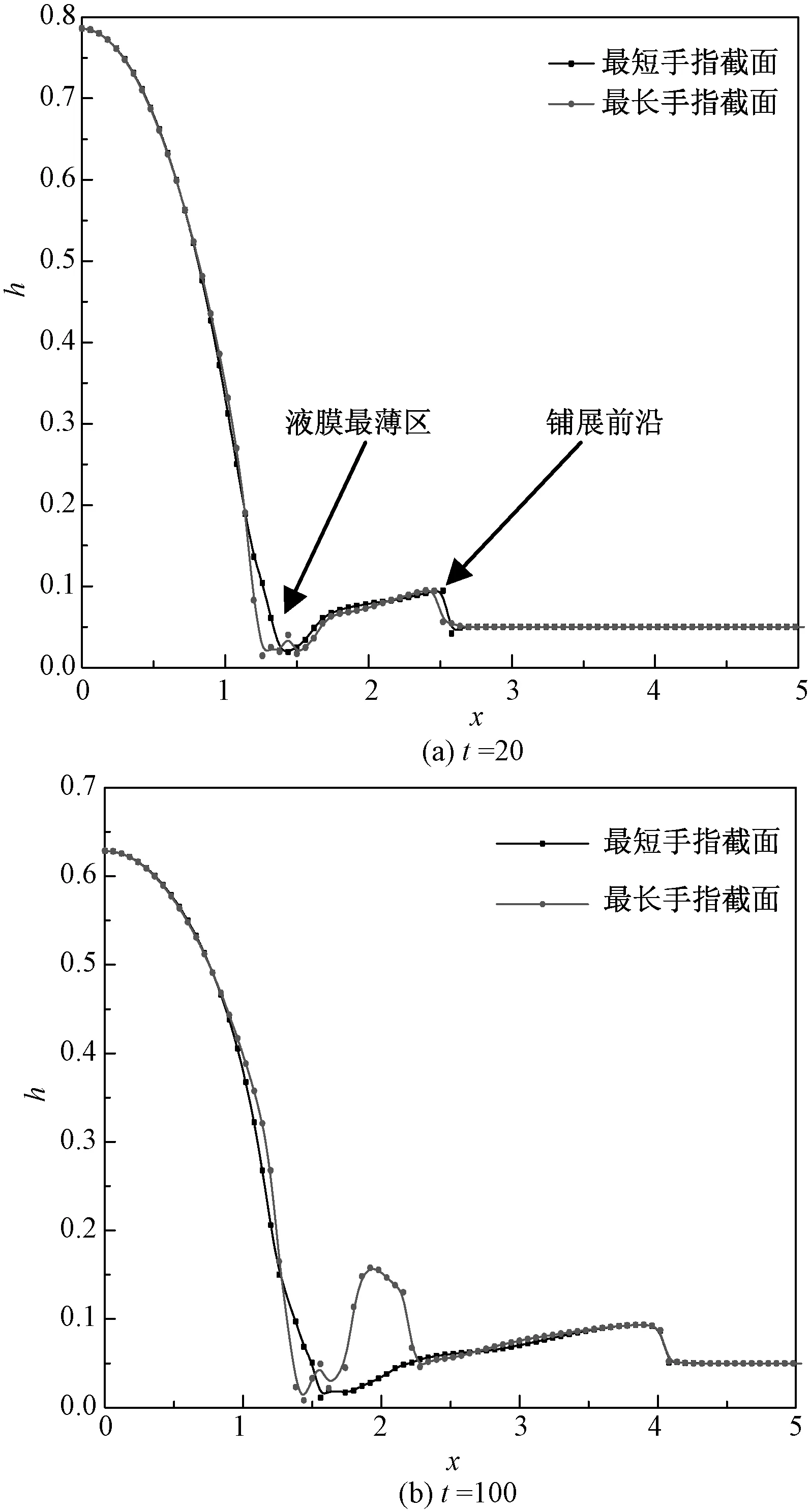
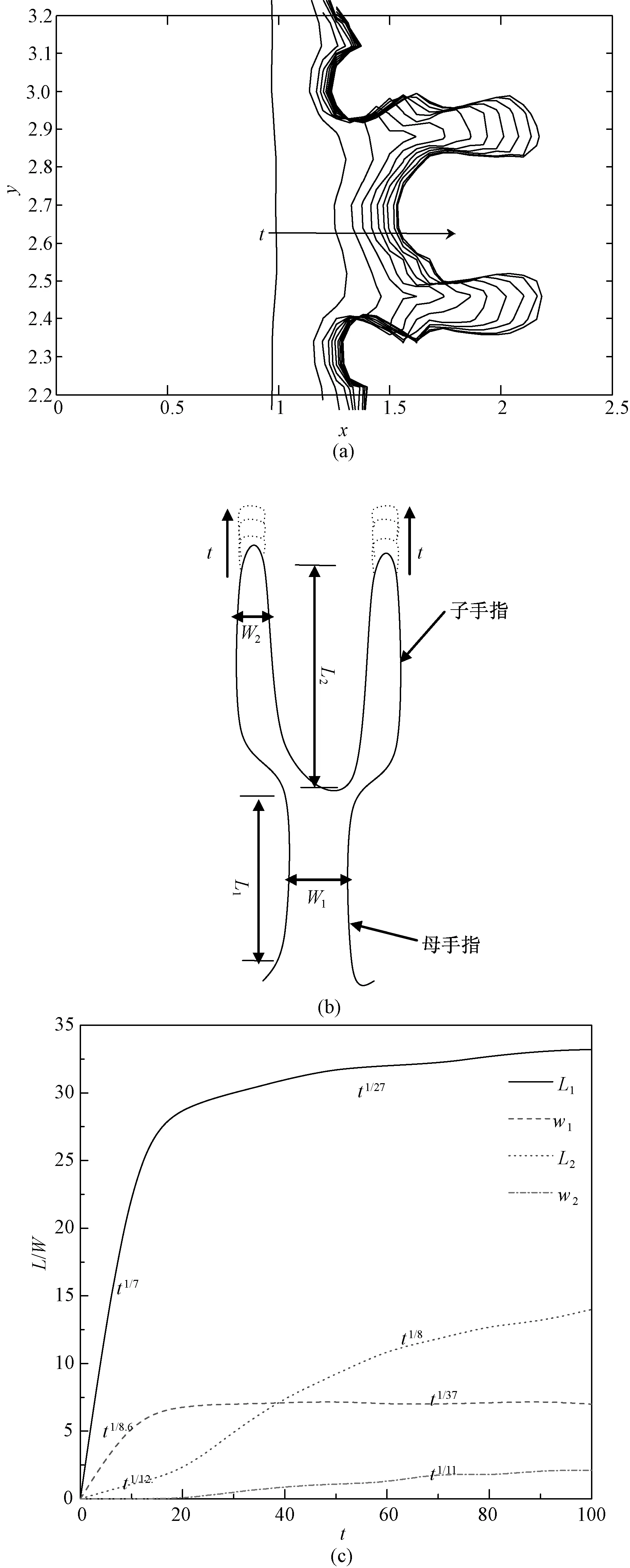
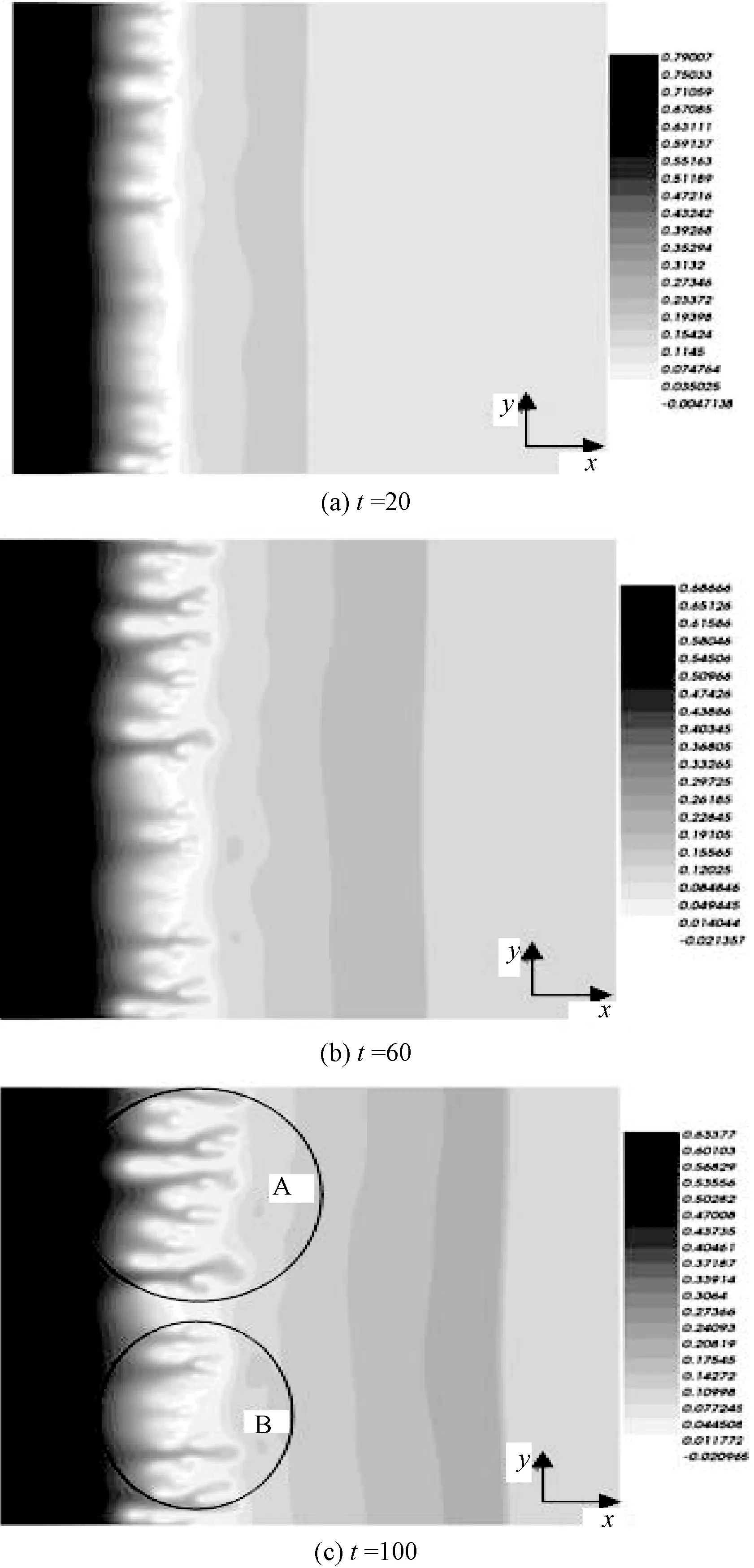
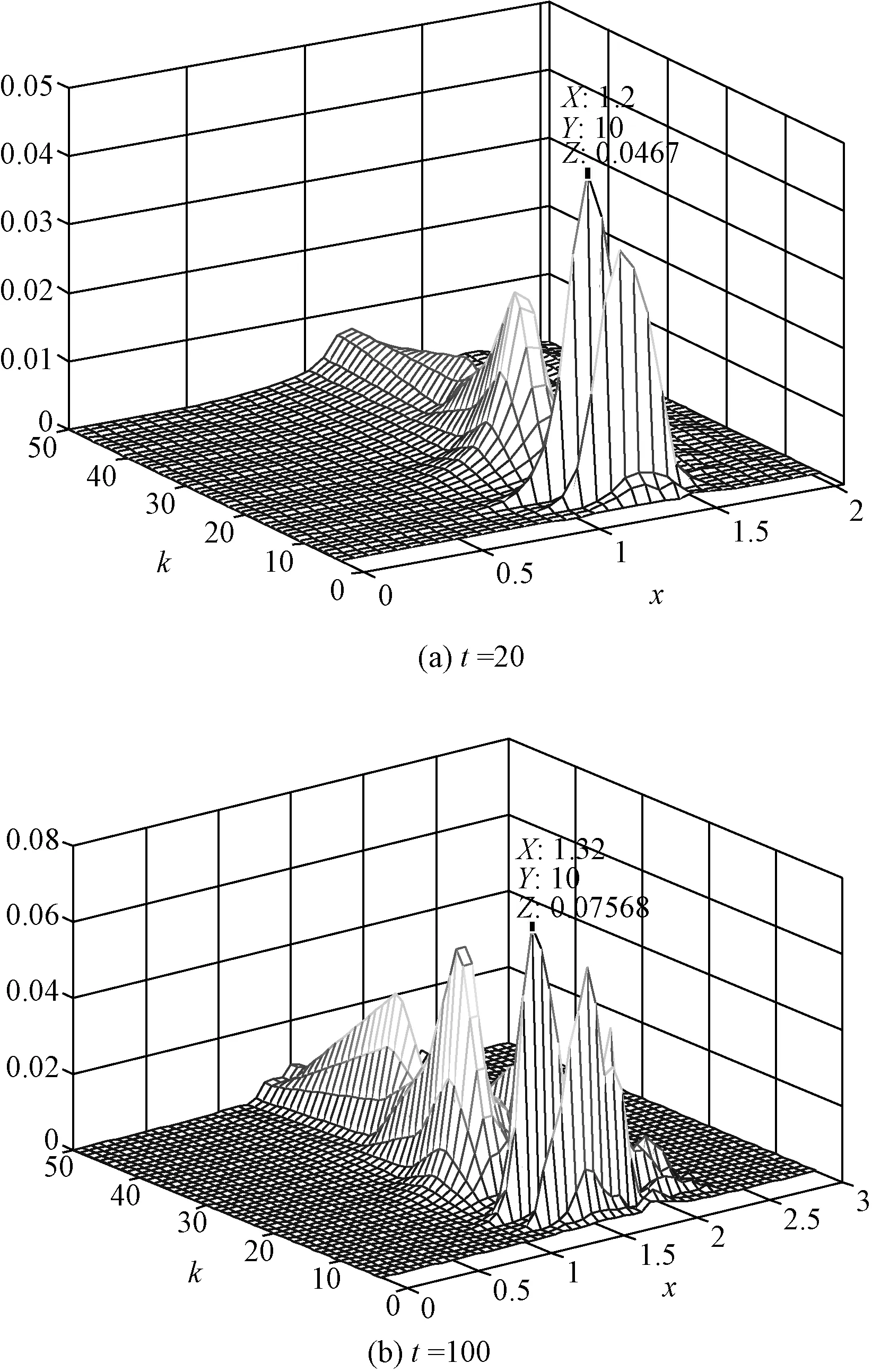
采用FREEFEM软件求解演化方程组(10)和(11)，选取0

无量纲参数毛细数C、Marangoni数及Peclet数是影响液膜厚度和活性剂浓度演化特征的重要参数，其范围为C=0.000 1～0.1，M=1～20，Pe=10～10 000[24]，为得到与实验结果和文献[12]相一致的指进现象，并分析其特征，通过多次模拟，参数选用如下：毛细数C=0.000 1，Marangoni数M=1，Peclet数Pe=10 000。

2.1 铺展过程中的指进现象

含活性剂液滴的三维铺展历程如图3所示，随时间t持续，铺展前沿处形成波状凸起，且凸起液膜厚度随t增加而逐渐增大。t=20时，最初在液滴底部(即液膜最薄区)施加的扰动已经生长为初生的手指形状，但此时手指长度仍较短，不同手指的长度(简称指长)和粗细(简称指宽)相对比较均匀。随时间延长，铺展持续发展，在液膜最薄区的液膜厚度变得更薄；当t=60时，部分手指开始分裂出子手指，指长也在不断增长；t=100时，指长和指宽不均匀特征更加突出：部分手指细小，部分手指粗大，即此时的指进现象特征更加显著。

图3 液滴铺展中的指进特征Fig.3 Fingering features in the droplet spreading

图4为铺展过程中的液膜厚度等高线。该图表明，随t延长，铺展前沿逐步向前推进、且该隆起处的液膜厚度在增大。在t=060内，液滴主体高度下降幅度较大，由初始液滴高度1.0降为0.67 713(图3(b)右侧图例所示)，而铺展前沿位置迅速推进到x=3.5处(图4(b))，即此阶段内液滴铺展速度较快；而在t=60100内，液滴中心下降速度减慢，仅由0.67 713下降到0.62 416(图3(c)图例所示)，铺展前沿推进速度变得缓慢，其所处位置由x=3.5推进到x=4.1(图4(c))，即此阶段内液滴铺展速度减缓。这是由于在液滴铺展前期，Marangoni效应显著，由此加快了液滴铺展速度；当t=60时，Marangoni效应的影响区域进一步增大，但其强度有所减弱，由此液滴铺展速度放缓[25]。另外，由图4可知，在液膜厚度最薄处衍生出指进现象，且随t增加，指进现象特征愈加明显，手指不断分裂、伸长，且长手指的指长变化较短手指快，这是由于长手指的存在减缓了其邻近短手指的生长速度。

图4 液膜厚度演化历程的等高线Fig.4 Contour of the film thickness evolution

为更清晰地显示液滴铺展过程中指进现象所在位置与液滴铺展前沿的关系，图5给出了t=20与100时指进现象中最长手指与最短手指所在位置的截面图，其中最长手指与最短手指位置在图4(c)中已标出(分别对应y=5.38与y=3.12)。图5表明，指进现象产生于液膜最薄区，液滴铺展前沿随时间延长不断向前扩展，手指也在不断伸长，最长手指的增长率快于最短手指的增长率，其长度之差逐渐增大，因而指进现象更加显著。

图5 不同y值对应的液膜厚度横截面图(最长手指对应截面y=5.38，最短手指对应截面y=3.12)Fig.5 The sectional view of the film thickness under different y values (y=5.38 and 3.12 denotes the longest and shortest fingers)

2.2 指长与指宽的增长率

为进一步分析指进现象的细节特征，以一个手指的分叉过程为例(分叉的手指位于如图4(c)中最短手指下方，见图4(c)右侧局部放大图)，在不同时刻追踪手指的发展，得到其指长与指宽的变化率，如图6所示。图6(a)为分叉手指在不同时刻下的演化细节特征；图6(b)为手指演化示意图，母手指分裂为两个子手指。其中母手指和子手指根部处的宽度以W1和W2表示，母手指根部到子手指根部的距离定义为母手指指长L1，类似地，子手指指长为L2。图6(b)中的虚线示意性地描绘了子手指的生长过程，其中指宽与指长均不断增加。图6(c)给出了不同手指的指长和指宽随时间的变化特征。由图6(c)可知，在t≤20时，母手指的指长L1和指宽W1分别以t1/7和t1/8.6的速率不断增长，即此阶段母手指在长度方向上较宽度方向的变化速率更快，同时母手指也有了分叉萌芽，只是分叉的子手指仅在指长上稍有变化，以速率～t1/12伸长，指宽并无变化；t≥20后，分叉后的子手指迅速伸长，速率为L2～t1/8，同时指宽W2也以t1/11速率在增长，而母手指的指长增长率减缓为t1/27，指宽W1变化甚微，仅为t1/37，这与Hamraoui等[4]的实验观察现象相吻合。在无初始扰动情形下，平整基底上含活性剂液滴的铺展半径始终以t1/6的速率稳定增长[24]，而由于初始扰动的影响，液滴铺展半径(产生于指进现象的液膜最薄处)随时间的增长速率出现了随机性，使得铺展半径出现长短不一的特征。

图6 指长与指宽的演化特征Fig.6 Evolution of the finger length and width

2.3 施加随机扰动时指进现象的功率谱特征

在液滴铺展过程中，存在一最危险扰动波数，由此导致液滴铺展呈现最不稳定特点[2, 12-14, 18]。现将前文初始条件中余弦函数形式的扰动波改为随机扰动形式，通过获得该情形下指进现象的功率谱特征，进而分析指进现象中的频率特性及影响液滴铺展稳定性的最危险扰动波数。

设定如下初始条件：

h0(x,y,0)=(1-x2+b)H(1-x)+bH(x-1)+A(y)exp(-5(x-1)2)

(17)

Γ0(x,y,0)=ΓcH(1-x)

(18)

图7 随机扰动下的指进特征Fig.7 Fingering feature under the random disturbance

其中，A(y)为在[-0.01,0.01]范围内的随机函数。图7为施加随机扰动下指进现象的二维图，该图显示出与余弦扰动时类似的指进现象形成过程。因施加初始扰动，t=20时，母手指初步形成，且其尖端已衍生出子手指萌芽；t=60时，母手指指长和指宽不断增大，子手指进一步长大，且手指整体数目增多，指进现象更加显著。但对比图3和图7可看出，在施加余弦扰动下，指进现象中的长短手指分布较匀称；而施加随机扰动下则指进现象中的长短手指分布均匀性较差，呈随机特征：如图7(c)所示，t=100时，A区域手指分布密集且较长，而B区域手指分布稀疏，手指也较短、不匀称。另外，施加随机扰动下指进现象手指呈现的随机特征，也更加符合实验中观察到的结果。

图8 随机扰动下的液膜厚度功率谱图Fig.8 Power spectrum of the film thickness under the random disturbance

在施加随机扰动下，为进一步获得影响其铺展过程的最危险扰动波数，图8给出了t=20和t=100时的液膜厚度功率谱图。该图是采用MATLAB将数值模拟结果中y方向上的数据通过傅里叶变换得到。由图可知，最初阶段，t=20时，小的扰动波数(如k=7，10，20)具有较高的扰动能量；随t增加，t=100时，较大的扰动波数(k=24、33)开始影响液滴铺展过程；但在液滴铺展过程中，具有最高扰动能量的扰动波数k值始终为10，这与稳定性研究中所得结果基本一致[12]。在x方向上，所有的扰动能量集中于液膜厚度最薄处，这也是导致铺展过程不稳定性最强，并出现指进现象的区域。

3 结 论

通过数值模拟研究了含不溶性活性剂液滴铺展过程中的指进现象，分析了指进现象的形成和发展历程，得到了指长和指宽的增长率及液膜厚度功率谱图。主要结论如下：

(1) 由于在液滴铺展前期，Marangoni效应显著，因而可加快液滴铺展速度，在t=0～60时，铺展前沿迅速推进至x=3.5处；当t=60时，Marangoni效应的影响区域进一步增大，但其强度有所减弱，由此液滴铺展速度放缓；t=60～100时，铺展前沿仅由x=3.5推进到x=4.1。

(2) 液滴铺展过程中，指进现象形成于液滴底部的液膜厚度最薄区。在铺展前期，t≤20时，手指逐渐形成，且指长和指宽逐渐增长；在铺展中后期，母手指出现分叉，形成子手指，且子手指数目不断增多，子手指指长和指宽不断增长；而母手指的指宽几乎不变，指长增长缓慢；

(3) 在初始时刻施加余弦扰动和随机扰动下的指进现象总体上类似，但施加随机扰动下指进现象呈现的随机特征更加符合实验结果；液膜厚度的功率谱表明，指进现象形成初期，小扰动波数具有较高的扰动能量，但在中后期，较大的扰动波数具有较高的扰动能量；在当前计算条件下，最危险扰动波数为k=10。

[1] 朱君悦，段远源，王晓东，等. 流体在固体表面的超铺展特性的研究进展[J].化工学报，2014， 65(3)：765-776.

[2] CRASTER R V，MATAR O K.Dynamics and Stability of Thin Liquid Films[J].Review of Modern Physics，2009，81(7-9)：1131-1198.

[3] TROIAN S M，WU X L，Safran S A. Fingering instability in thin wetting films[J].Physical Review Letters,1989,62(13):1496-1500.

[4] HAMRAOUI A，CACHILE M，POULARD C，et al.Fingering phenomena during spreading of surfactant solutions[J]. Colloids and Surfaces A, 2004, 250(1-3): 215-221.

[5] AFSAR-SIDDIQUI A B，LUCKHAM P F，MATAR O K.Unstable spreading of an anionic surfactant on liquid films. part I： sparingly soluble surfactant[J].Langmuir，2003， 19(3)：696-702.

[6] AFSAR-SIDDIQUI A B， LUCKHAM P F， MATAR O K.Unstable spreading of an anionic surfactant on liquid films. Part II：highly soluble surfactant[J].Langmuir，2003，19(3)：703-708.

[7] MARMUR A，LELAH M D.The spreading of aqueous surfactant solutions on glass[J] .Chemical Engineering Communications，1981，13(1-3)：133-143.

[8] 杨兆中，李小刚，蒋梅,等.指进现象模拟研究的回顾与展望[J]. 西南石油大学学报(自然科学版),2010，32(1)：85-88，8-9.

[9] STEVENSON K，FERER M, BROMHAL G S，et al.2-D network model simulations of miscible two-phase flow displacements in porous media: effects of heterogeneity and viscosity[J].Physica A，2006，367(1)： 7 -24.

[10] 李维仲，董波，宋永臣.水平通道内黏性指进现象的LBM模拟[J]. 大连理工大学学报, 2012，52(3)：343-349.

[11] TROIAN S M，HERBOLZHEIMER E，SAFRAN S A， et al.Fingering instability of driven spreading films[J].Europhysics Letters，1989，10(1)： 25-30.

[12] WARNER M R E，CRASTER R V，MATAR O K.Fingering phenomena associated with insoluble surfactant spreading on thin liquid films[J]. Journal of Fluid Mechanics，2004，510：169-200.

[13] WARNER M R E，CRASTER R V，MATAR O K.Fingering Phenomena Created by a Soluble Surfactant Deposition on a Thin Liquid Film[J].Physics of Fluids，2004，16(8)：2933-2951.

[14] EDMONSTONE B D，MATAR O K，CRASTER R V.Surfactant-induced fingering phenomena beyond the Critical Micelle Concentration[J].Journal of Fluid Mechanics，2006，564：105-138.

[15] EDMONSTONE B D，MATAR O K，CRASTER R V.Surfactant-induced Fingering Phenomena in Thin Film Flow down an Inclined Plane[J].Physica D，2005，209：62-79.

[16] FAST P，SHELLEY M J.Moore’s law and the Saffman-Taylor instability[J] .Journal of Computational Physics，2006，212：1-5.

[17] LI Chunxi， PEI Jianjun， YE Xuemin.Spreading of Droplet with Insoluble Surfactant on Corrugated Topography[J].Physics of Fluids，2014，26：092103.

[18] 李春曦，陈朋强，叶学民.含活性剂液滴在倾斜粗糙壁面上的铺展稳定性[J].物理学报，2015，64(1)：014702.

[19] 李春曦，杨保才，叶学民.分离压对不同基底上含活性剂液滴铺展特征的影响[J].华北电力大学学报，2015,42(3)：71-77.

[20] 赵亚溥.表面与界面物理力学[M].北京：科学出版社.2012.

[21] 叶学民，姜凯，李春曦.含胶束结构的活性剂溶液非均匀铺展演化模型研究[J].华北电力大学学报，2012,39(3)：88-93.

[22] 王松岭，李春曦，叶学民.液滴铺展过程中受活性剂浓度影响的分离压模型研究[J].华北电力大学学报，2011,38(1)：81-85.

[23] 李慧君，王佩.竖直管内纯蒸汽凝结换热液膜分布及换热特性[J].华北电力大学学报，2015,42(1)：80-84.

[24] 李春曦，裴建军，叶学民.波纹状基底上含不溶性活性剂液滴的铺展过程[J].化工学报，2013，64(9)：3308-3316.

[25] 李春曦，裴建军，叶学民.倾斜粗糙壁面上含不溶性活性剂溶液的动力学特性[J].物理学报，2013，62(21)：214704.

Fingering Feature During Droplet Spreading Containing InsolubleSurfactuants on Precursor Film

YE Xuemin, WANG Yuanyuan, LI Chunxi

(Key Laboratory of Condition Monitoring and Control for Power Plant Equipment,North China Electric Power University, Baoding 071003, China)

When a droplet with surfactants is deposited on the precursor film or solid substrate, the spreading process will be presented due to the concentration gradient of the surfactant. Due to the existence of initial disturbance, the thinning region of the drop spreading shows complex patterns, namely, the fingering phenomena. In the present paper, the fingering phenomenon during the spreading of a droplet with insoluble surfactants on precursor film is recreated by numerical simulation, and the growth rates of finger length and width of different fingers are examined. The power spectrum of the film thickness is investigated and the most unstable wave number is found. The results show that the fingers appear in the thinning region at the bottom of drop, and these fingers become longer, wider and bifurcate with the spreading process. The fingering phenomena present similar features when exerting different forms of initial disturbance: the finger length distribution is symmetrical under the cosine disturbance while the finger length distribution uniformity is poor under the random disturbance. The most unstable perturbation wave numberkis 10 under the present calculation parameters.

surfactant droplet; spreading; fingering phenomena; power spectrum

10.3969/j.ISSN.1007-2691.2016.05.12

2015-11-04.

国家自然科学基金资助项目(11202079);河北省自然科学基金资助项目( A2015502058)；中央高校基本科研业务费资助项目(13MS97).

O363； TQ021

A

1007-2691(2016)05-0075-08

叶学民(1973-)，男，教授,主要从事流体动力学理论及应用、强化传热传质技术等方面的研究工作。