例析间接测量法的实际应用
2016-12-06温卫国
温卫国
(江苏省常熟市浒浦高级中学,江苏 常熟 215512)
·试题研究·
例析间接测量法的实际应用
温卫国
(江苏省常熟市浒浦高级中学,江苏 常熟 215512)
微小量的测量是实际应用中经常遇到的问题,本文介绍了5种利用间接方法测量微小量的原理,使学生体验到物理原理在实际生活中的应用.
间接测量法;微小量测量;物理应用
物理学是一门实验科学,但在实际生活中,有些微小量的测定,无法利用工具直接测得,需要借助物理原理和数学知识来间接测量.在平时的教学实践中,经常会遇到此类问题,本文对间接测量的实验问题作简单分析.
例1:图1为测量微小厚度变化的装置示意图,在工作台A上放标准件,标准件上面压杆C的顶部有一小平面镜.一束光线从标尺垂直射向平面镜,反射后落在标尺刻度P处.现撤去标准件,换上待测工件,如待测工件比标准件厚Δx,则压杆顶部的小平面镜就会绕轴O转过一微小角度θ,使反射光线落在Q处.已知平面镜距标尺距离为L1,平面镜中心距O点距离为L2.PQ=Δs.求待测工件与标准件的厚度差Δx.(当θ很小时,tan2θ=2tanθ)
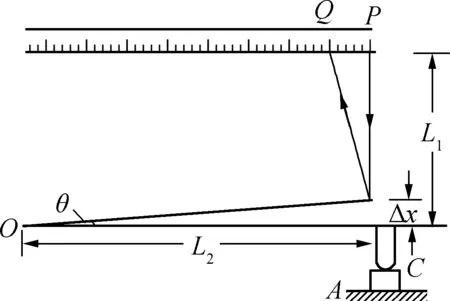
图1
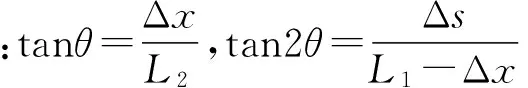
说明:这种测量微小量变化是利用光学原理,将微小厚度变化加以放大后测出,这一方法在实际应用中较为常见.
例2:电梯修理工、牵引专家和赛艇运动员常需要知道绳子或金属线中的张力,可又不能方便地到达绳、线的自由端去测量.一家英国公司制造出一种夹在绳子上的仪表,用一个杠杆使绳子上的某点有一个微小偏移量,如图2所示,仪表很容易测出垂直于绳的恢复力,推导一个能计算绳中张力的公式,如偏移量为12mm,恢复力为300N,试计算绳中张力.

图2
解析:设绳中张力为
T
,仪器对绳的拉力
F
可分解为拉绳的两个力
F
1
、
F
2
,而
F
1
=
F
2
=
T
,如图3所示,由
F
1
、
F
2
、
F
构成一个菱形,依图中几何关系,有
.又因形变微小,所以sin
θ
≈tan
θ
,故
.当
F
=300N,
δ
=12mm时,得到
T
=1.56×10
3
N.

图3
说明:尽管绳中的张力不能直接测量,但利用力的合成与分解原理,通过测定一个微小偏移量,很容易算出绳中的张力.
例3:如图4所示,在卡文迪许实验中,两个大球与两个小球球心的距离均为r=10cm,连接两个小球的轻杆长L=50cm,小球质量m=10g,大球的质量m′=10kg,根据悬丝偏转的角度计算出悬丝产生的扭转力矩M是3.4×10-10N·m,试求引力常量G.
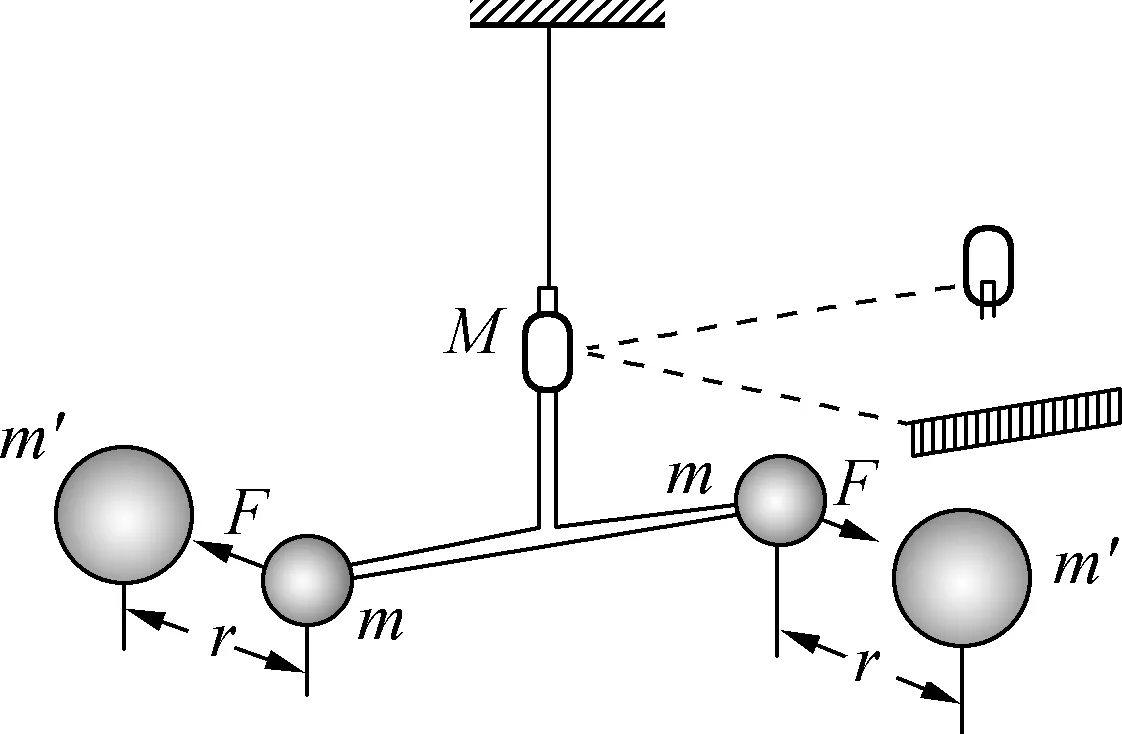
图4
说明:利用扭秤实验不仅可以测量万有引力常量,同样可以测出静电力常量k的数值.
例4:在“用油膜法估测分子大小”的实验中,油酸酒精溶液的浓度为每104mL溶液中有6mL纯油酸,1mL溶液中有50滴.把1滴该溶液滴到盛水的浅盘里,待水面稳定后,将玻璃板放在浅盘上,在玻璃板上描出油膜的轮廓,随后把玻璃板放在坐标纸上,其形状如图5所示,坐标纸上正方形小方格的边长为20mm.求:
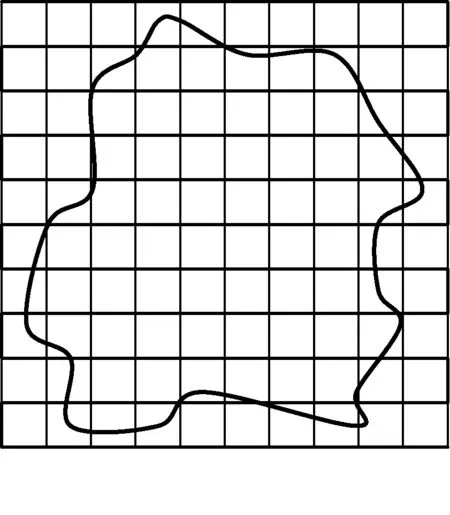
图5
(1) 油酸膜的面积是多少?
(2) 每一滴油酸酒精溶液中含有纯油酸的体积是多少?
(3) 根据上述数据,估算出油酸分子的直径.
解析:(1) 油酸薄膜所覆盖的坐标纸方格为58个,故油膜面积S=58a2=58×(20×10-3)2m2=2.32×10-2m2.
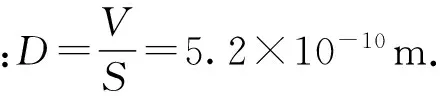
说明:虽然分子直径数量级很小,但通过建立适当的模型,测出相应的体积和面积,同样可以求得.
例5:用红光做光的干涉实验时,已知双缝间的距离为0.2×10-3m,测得双缝到屏的距离为0.700m,如图6所示,分划板中心刻线对齐第一级亮条纹中央时手轮读数为0.200×10-3m,第五级亮纹所在位置为9.893×10-3m,求红光的波长.
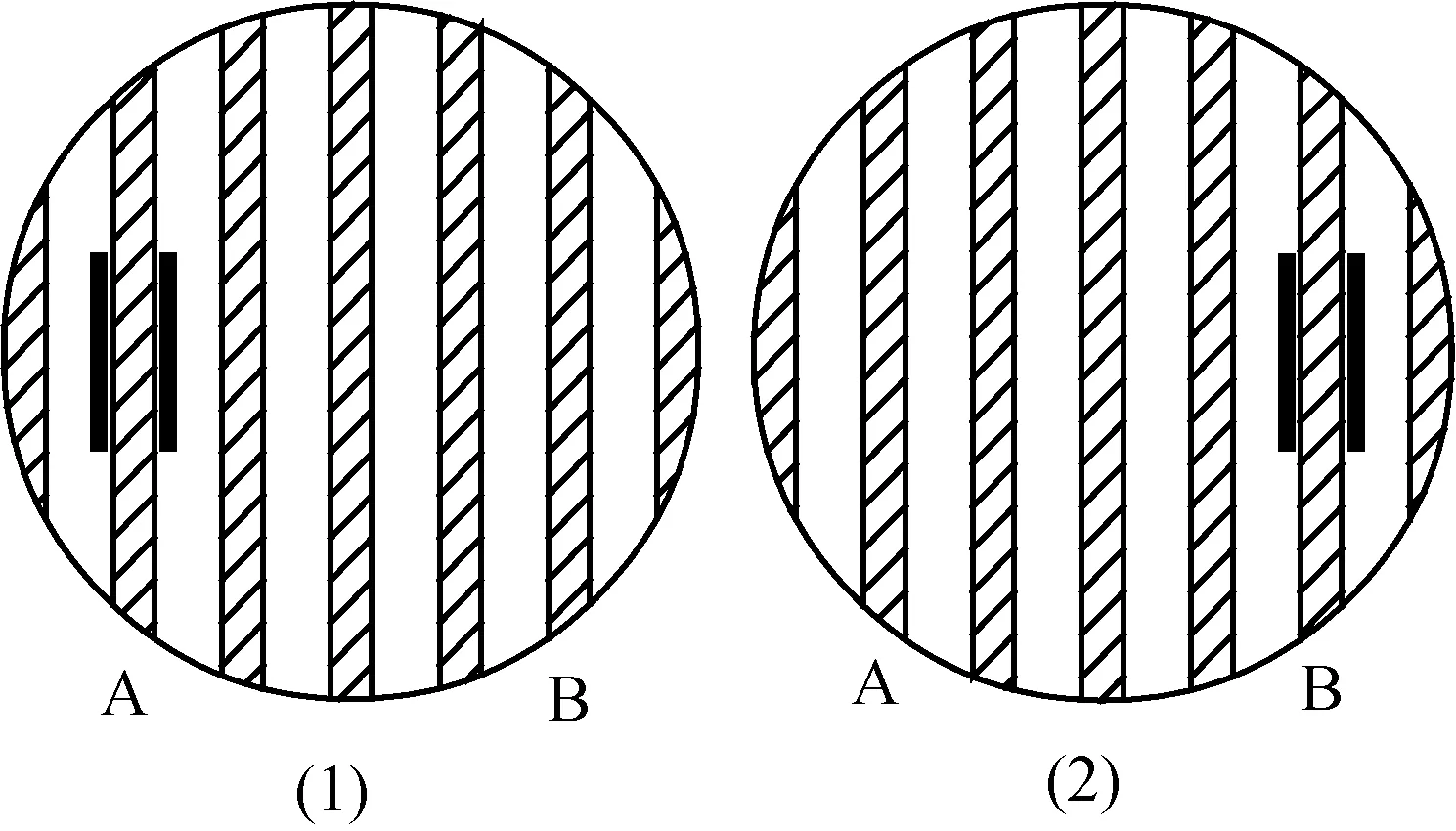
图6
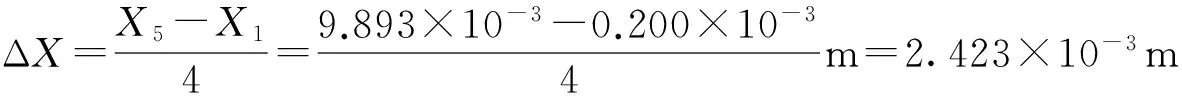
说明:利用光的干涉实验来测量光的波长,是一种间接而准确的方法,同时,借用薄膜干涉实验还可以检查工件的质量.
其实在实际生活中还有很多应用物理知识进行微小量测量的问题,只要我们稍加留意,积极引导,不断创新,学生学习物理的兴趣一定会不断提高,应用知识解决物理问题的能力也一定会越来越强.
