基于背景值与初始条件优化的非等间距GM(1,1)模型

胡大红

（汉口学院 计算机科学与技术学院，湖北 武汉 430000）

基于背景值与初始条件优化的非等间距GM(1,1)模型

胡大红

（汉口学院 计算机科学与技术学院，湖北 武汉 430000）

利用非等间距GM(1,1)模型一次累加生成序列近似满足指数规律优化其背景值，再利用最小二乘法，由模拟序列和原始序列的一次累加生成值的偏差平方和最小对模型的时间响应函数的参数进行优化，从而建立基于背景值与初始条件同时优化的非等间距GM(1,1)模型，并通过实例验证此模型的有效性与可行性.

灰色系统理论；非等间距GM(1,1)模型；背景值优化

灰色GM(1,1)预测模型是对小样本、贫信息系统进行建模的重要预测模型.自提出以来，主要应用于等间距离散数据的建模预测[1-5].在实际生活和工程应用中，有很多数据都属于非等间距采样，对于这一类数据，建模方法与传统等间距数据建模方法不同，需要考虑时间序列对数据发展的影响.文献[6-9]对非等间距序列的建模方法进行了研究，文献[6]以非等间距序列的间距为乘子，对非等间距序列建立优化模型，文献[7]以平均相对误差绝对值最小为目标，以模型参数之间的关系为约束，构建了一个非线性优化模型实现非等间距GM(1,1)模型的参数估计，文献[8]以一次累加观测值与模拟值的残差平方和最小为条件，对非等间距GM(1,1)模型的参数进行优化，文献[9]通过重构背景值建立非等间距GM(1,1)优化模型.这些研究为非等间距序列建立灰色预测模型提供了有益的探索，但建模精度有待进一步提高.

本文试图通过研究非等间距原始序列的特点和GM(1,1)模型的建模机理，在优化背景值的基础上，根据最小二乘法，以原始序列的一次累加生成值与模拟值之差平方和最小为条件，构建非等间距GM(1,1)模型的时间响应函数的优化模型.

1 非等间距GM(1,1)模型

对X(1)建立白化微分方程

对应灰微分方程为

其中z(1)(ki)是x(1)(ki)在[ki-1,ki]上的背景值.灰色微分方程的参数a,b的最小二乘估计，其中，则白化微分方程的时间响应函数为

2 非等间距GM(1,1)模型的优化

3 工程实例

本文采用文献[6-9]中的工程技术实例来建模.该序列是P.G福雷斯研究了钛合金疲劳强度随温度变化的实验结果，这是一个非等间距序列.文献[6]以序列的间距Δki为乘子构造一次累加生成序列，以和原始GM(1,1)模型相同的方法建立非等间距GM(1,1)模型，文献[7]提出了非等间距GM(1,1)幂模型的灰色微分方程，以平均相对误差绝对值最小化为目标，以模型参数之间的关系为约束，构建了一个非线性优化模型对非等间距GM(1,1)幂模型的参数γ进行估计，从而建立优化的非等间距GM(1,1)幂模型.按照本文所建立的非等间距GM(1,1)模型，文献[6]，[7]所建立的模型分别对原始数据序列进行建模，然后进行对比分析.

本文所建立的非等间距GM(1,1)模型记为优化模型，其时间响应函数为

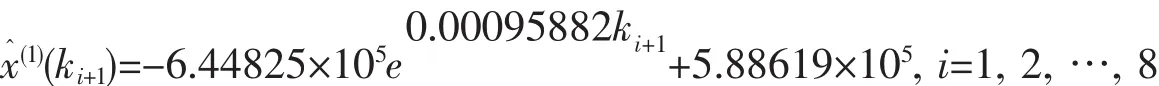
3个模型模拟效果的比较如表1.

从表1可以看出，本文建立的优化模型的模拟效果的平均相对误差是0.43%，文献[6]和文献[7]所建模型的模拟效果的平均相对误差分别是0.76%和0.75%，本文建立的优化模型的最大相对误差-1.44%，而文献[6]和文献[7]所建模型的最大相对误差分别是2.24%和-2.43%，从平均相对误差和最大相对误差来看，本

文所建的优化模型的模拟效果更优.

表1 三个模型的的模拟值与实际值的比较

三个模型的预测效果的比较如表2，可以看出，本文建立的优化模型的预测相对误差是0.33%，而文献[6]和文献[7]所建模型的预测相对误差分别是-2.70%和2.53%，本文所建立的优化模型的预测效果更优.

表2 三个模型的的预测值与实际值的比较

4 结语

由于非等间距序列在实际生活和工程应用等领域大量存在，所以对非等间距序列的建模进行研究有非常重要的现实意义.本文通过分析非等间距序列的特点和GM(1,1)模型的建模机理，提出了一种对背景值和时间响应函数中的参数同时进行优化的建模方法，实例表明该优化模型对于非等间距序列的拟合和预测效果均较好，可以提高非等间距GM(1,1)模型的模拟精度和预测精度.

[1]肖新平,刘 军,郭 欢.广义累加灰色预测控制模型的性质及优化[J].系统工程理论与实践,2014,34(6）:1547-1556.

[2]郭晓君,刘思峰,方志耕,等.灰色GM(1,1，tα)模型与自忆性原理的耦合及应用[J].控制与决策,2014,29(8):1447-1452.

[3]王正新.时变参数GM(1,1)幂模型及其应用[J].控制与决策,2014,29(10):1828-1832.

[4]刘思峰,党耀国,方志耕,等.灰色系统理论及其应用[M].3版.北京:科学出版社,2004:10-16.

[5]徐 宁,党耀国,丁 松.基于误差最小化的GM(1,1)模型背景值优化方法[J].控制与决策,2015,30(2):283-288.

[6]王钟羡,吴春笃,史雪荣.非等间距序列的灰色模型[J].数学的实践与认识,2003,33(10):16-20.

[7]王正新,党耀国,刘思峰.非等间距GM(1,1)幂模型及其工程应用[J].中国工程科学,2012,14(7):98-102.

[8]崔立志,刘思峰,吴正朋.非等间距GM(1,1)模型时间响应函数的优化[J].统计与决策,2009(13):9-10.

[9]戴文战,李俊峰.非等间距GM(1,1)模型建模研究[J].系统工程理论与实践,2005,25(9):89-93.

Unequal Interval GM(1,1)Model Based on Optimization of Background Value and Original Condition

HU Dahong
(Computer Science&Technology College,Hankou University,Wuhan 430000,China)

The background value of the unequal interval GM(1,1)model is optimized while its first accumulated generating series satisfy the approximate exponential rules.According to the method of least squares,the pending coefficient of the time response function is optimized when the sum of the squared differences of the first accumulated generating values and the simulative values is the smallest,then the unequal interval GM(1,1)model optimized both the background value and the original condition is obtained.This optimized model doesn’t need to select the initial condition,and an example is given to show the effectiveness and feasibility of this model.

Grey system theory;Unequal interval GM(1,1)model;Background value optimization

N941.5

A

2095-4476（2016）11-0020-03

（责任编辑：饶 超）

2016-10-11;

2016-11-02

湖北省教育厅科研项目(B2015504)

胡大红(1974—),女,湖北随州人,汉口学院计算机科学与技术学院副教授.