一类基于比率和带收获率的捕食反应扩散模型的全局渐近稳定性

孟义杰

（湖北文理学院 数学与计算机科学学院，湖北 襄阳 441053）

一类基于比率和带收获率的捕食反应扩散模型的全局渐近稳定性

孟义杰

（湖北文理学院 数学与计算机科学学院，湖北 襄阳 441053）

讨论一类在齐次Neumann边界条件下具有扩散项和按比率收获的捕食模型解的全局渐近稳定性，并利用改进的迭代方法和比较原理讨论其非负半平凡解和正平衡解的全局渐近稳定性，得到了一些充分条件．

捕食模型；齐次Neumann边界；非负半平凡解；平衡解；全局渐近稳定性

1 引言

近年来，捕食-食饵模型具有的动力学行为已成为很多生物数学和微分方程学者所研究的热点问题．由于现实生活中的生物现象复杂多样，因此描述捕食者与食饵之间相互作用的数学模型也很多，比如Beddington-DeAngeli、Holling类型、阶段结构、饱和与竞争项和比率型功能反应等，并得到很多结果[1-5]．而越来越多的生物现象表明，当捕食者不得不搜寻食物时，用基于比率依赖型功能反应函数来描述捕食者和食饵之间的相互作用更切合实际，即每一个捕食者个体的增长率应该是关于食饵和捕食者数量比的函数．由于人类活动也对生物种群密度变化产生的影响越来越大，其捕获行为对种群密度的改变这一现象引起了很多学者和科研人员的广泛关注，并已取得一些研究成果，如Chakraborty K.,Jana S.和Kar T.K.在文献[4]中研究了一类具有阶段性结构的捕食与被捕食收获模型的全局动力行为及分歧，Lan and Zhu在文献[6]中研究了一类带有Beddington-DeAngeli功能反应函数的捕食模型在常数收获率下解的性质．本文将讨论基于比率和带收获的反应扩散捕食模型，即

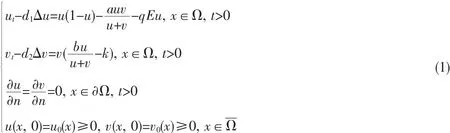
其中，u和v是定义在RN上一个具有光滑边界∂Ω的有界区域Ω中，分别表示两种群的数量．a,b,q,E和k为正常数，a表示捕食者对食饵的捕获率，b表示食饵对捕食者的转化率，k表示捕食种群在没有食饵时的自然死亡率，q表示外界对食饵种群的捕捞系数，E表示捕捞强度，0＜qE＜1．n是边界∂Ω的单位外法线方向向量，初值u0(x)和v0(x)是连续函数．

注意到式(1)有唯一的非负全局解(u,v)，并且如果u0和v0都不恒等于零，那么解(u,v)为正，即对一切t＞ 0，都有

文献[7]研究了模型(1)的耗散性，正平衡解的局部渐近稳定性和局部分歧解的存在性．本文主要利用改进的上下解迭代方法[8-10]和比较原理讨论该模型的非负半平衡解和正平衡解的全局渐近稳定性．

2 主要结果和证明

系统(1)经过计算可知，当b≤k时，存在惟一的半平凡非负常数稳态解(1-qE,0)；当b＞k,时，存在惟一的正常数稳态解(u*,v*)，且满足

[1]CANTRELL R S,COSNE C.On the dynamics of predator-prey models with the Beddington-DeAngelis functional response[J]．Journal of Mathematics Analysis&Application,2001,257(1):206-222．

[2]BAZYKIN A D.Nonlinear Dynamics of Interacting Populations[M].Singapore:World Scientific,1998．

[3]KO W,RYU K.Qualitative analysis of a predator-prey model with Holling type II functional response incorporating a prey refuge[J].Journal of Differential Equations,2006,231(2):534-550．

[4]CHAKRABORTY K,JANA S,KAR T K.Global dynamics and bifurcation in a stage-structured prey-predator fishery model with harvesting[J]. Applied Mathematics and Computation,2012,218(18):9271-9290．

[5]WANG M X,WU Q.Positive solutions of a prey-predator model with predator saturation and competition[J].Journal of Mathematical Analysis& Applications,2008,345(2):708-718．

[6]LAN KUNQUAN,ZHU CHANGRONG.Phase portraits of Predator-prey systems with harvesting rates[J].Discrete&Continuous Dynamical Systems,2012,32(3):901-933．

[7]刘 清,李艳玲.一类基于比率和带收获率的捕食模型解的性质[J].河北师范大学学报:自然科学版,2013,37(2):119-124．

[8]WANG Y F,MENG Y J.Asymptotic behavior of a competition-diffusion system with time delays[J].Mathematical&Computer Modelling,2003, 38(5-6):509-517．

[9]MENG YIJIE,WANG YIFU.Asymptotic behavior of a predator-prey system with time delays[J].Electronic Journal of Differential Equations,2005(4): 357-370．

[10]MENG YIJIE,XIAO SHIWU.Global asymptotic behavior of a predator-prey diffusion system with Beddington-DeAngelis function response[J].Journal of Partial Differential Equations,2014(2):125-135．

Global Asymptotic Stability of a Predator-Prey Reaction Diffusion Model with Ratio-dependent and Harvesting Rate

MENG Yijie
(College of Mathematical and Computer Sciences,Hubei University of Arts and Science,Xiangyang 441053,China)

In this paper,we consider the global asymptotic stability of solutions of a predator-prey reactiondiffusion model with ratio-dependent and harvesting function response under homogeneous Neumann boundary condition.Via iteration method and the parabolic equation comparison principle,the global asymptotical stability of the nonnegative semi-trivial solutions and positive steady-state solution are discussed,and some sufficient conditions are given.

Predator-prey model;Homogeneous Neumann boundary;Nonnegative semi-trivial solutions；Steady-state solution；Global asymptotical stability

O175.26

A

2095-4476（2016）11-0005-05

（责任编辑：饶 超）

2016-09-01

国家自然科学青年基金(11501186)

孟义杰(1972—),男,湖北襄阳人,湖北文理学院数学与计算机科学学院副教授.