空心板梁桥桥面连续构造的受力特性试验
2016-12-06王城泉申永刚
王城泉, 申永刚, 王 岗, 谢 旭
(浙江大学 土木工程学系,浙江 杭州 310058)
空心板梁桥桥面连续构造的受力特性试验
王城泉, 申永刚, 王 岗, 谢 旭
(浙江大学 土木工程学系,浙江 杭州 310058)
针对现有拉杆式桥面连续构造易发生开裂、渗水等病害,提出适用于空心板梁桥的拱型桥面连续构造形式,并用实桥荷载试验验证了抗开裂的有效性.通过理论计算和数值仿真,确定空心板梁桥拱型桥面连续构造的拱跨、矢高和分隔缝形式.在车辆荷载或负温度梯度作用下,梁端上翘不会引起拱型桥面连续上移,受拉连接钢筋使拱顶产生正弯矩,混凝土受压;在正温度梯度作用下,钢板分隔缝使桥面铺装压应力有效地传至桥面连续混凝土,抵消了拱顶负弯矩所产生的拉应力.试验结果表明,拱型桥面连续可以使拱顶混凝土达到受压状态,且压应力随荷载增大而增大,而拉杆式桥面连续混凝土始终为受拉状态,且拉应力随荷载增大而增大,无黏结钢筋与混凝土之间的滑移失效是拉杆式桥面连续混凝土受拉开裂的主要原因.
空心板梁桥;拱型桥面连续;拉杆式桥面连续;受力特性;荷载试验
我国公路中小跨径梁桥普遍采用桥面连续形式[1-3],其中以拉杆式桥面连续(debonded rebar link slab, DRLS)应用最为广泛.在拉杆式桥面连续构造中,连接钢筋在桥面连续区域采用无黏结构造形式,既传递桥面铺装的内力,又防止桥面连续混凝土受到钢筋拉力.理论上这种构造形式可以有效减小桥面连续混凝土的拉应力,但由于实际施工中连接钢筋无黏结措施易失效等问题,桥梁运营一段时间后,桥面连续混凝土常常因为受拉过大而开裂漏水.不仅影响行车的平顺性,还产生了桥墩腐蚀等一系列病害[4-6].桥面连续病害在国外也同样存在,美国曾对105座桥面连续简支梁桥(包括72座混凝土梁和33座钢梁)进行病害调查发现[7],除了桥面连续出现开裂,桥梁的其他功能都能满足设计要求,但这些病害明显增加了桥梁养护成本.
国内外许多学者对桥面连续的受力机理和病害防治措施进行了研究.沈青川[8]采用非线性有限元模型分析比较了拉杆式桥面连续和刚接桥面连续在加载历程中的应力变化和裂缝状态;丁勇等[9]将桥面连续的影响用弹簧刚度表示,提出一种带边界转动弹簧的简支梁模型,完善了桥面连续简支梁桥的力学分析理论;Wing等[10-11]先后对(debonded link slab,DLS)桥面连续进行了试验和理论分析,通过在梁缝设置一定长度的无黏结段来避免桥面连续与主梁直接作用;Alexander等[12]对桥面连续进行了疲劳试验研究,发现循环荷载作用下主梁转动和上翘使得桥面连续混凝土开裂;潘志炎等[13]提出带排水措施的植入式桥面连续构造,达到了分散应力、减缓混凝土开裂的作用;Qian等[14]对一种高延性水泥基复合材料(Engineered cementitious composite, ECC)桥面连续进行了理论分析,认为该材料能增加桥面连续的使用周期;Saber等[15]通过数值模拟和试验研究,认为玻璃纤维增强塑料(fiberglass-reinforced plastic, FRP)桥面连续能够更好地适应桥面连续的变形,满足耐久性需求;赵成栋[16]针对小箱梁桥提出一种带PBL剪力键的钢-混凝土组合板式桥面连续构造.2014年,王岗等[17]提出一种拱型桥面连续构造(arched link slab, ALS),通过数值分析证明这种新型桥面连续能够有效减小混凝土的拉应力.
该拱型桥面连续适用于空心板梁、T梁、小箱梁等所有常用简支梁桥,但对于不同的桥型和跨径,具体构造形式有所区别.本文针对空心板梁桥,给出了拱型桥面连续的具体构造尺寸,并将应用于一座三跨简支空心板梁桥.作为对比,在该桥上同时布置了拉杆式桥面连续,通过桥梁荷载试验实测了2种桥面连续在多级荷载下的混凝土和连接钢筋应变.数值计算和试验研究验证了本文给出的空心板梁拱型桥面连续构造防止混凝土开裂的有效性.同时通过实测无黏结连接钢筋与混凝土的应变,揭示了拉杆式桥面连续混凝土开裂的重要原因,为研究桥面连续病害提供了试验依据.
1 有限元模型
1.1 工程概况
如图1所示,试验桥梁为一座三跨预应力混凝土空心板梁桥,配跨为3×16 m,桥宽为0.5 m(护栏)+6 m+0.5 m(护栏),斜交30°.空心板梁高80 cm,宽1.25 m,计算跨径15.3 m,支座中心线到梁端部距离为33 cm,混凝土等级为C50,预应力钢绞线设计标准强度为1 860 MPa.桥面铺装厚15 cm.桥墩①、②的梁缝宽4 cm,相邻板式橡胶支座纵向间距d=70 cm.设计荷载为汽车荷载公路-I级,人群荷载3.0 kN/m2.在墩1上布置了拱型桥面连续,墩2上布置了拉杆式桥面连续.在相同车辆荷载情况下,对2种桥面连续混凝土的应力进行测试和对比.
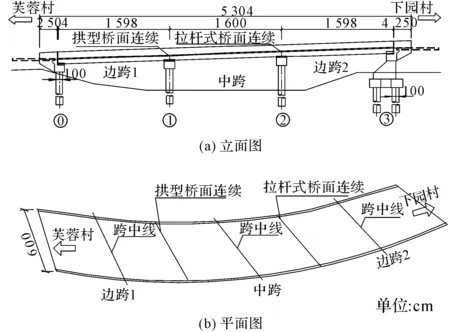
图1 三跨预应力混凝土空心板梁桥示意图Fig.1 Layout of three span prestressed concrete hollow slab bridge
1.2 全桥有限元模型

图2 全桥有限元模型Fig.2 Finite element model of test bridge
如图2所示,利用ABAQUS建立全桥有限元模型.混凝土选用8结点六面体实体单元(C3D8R);钢筋选用两节点线性三维桁架单元(T3D2),采用Embedded region方式嵌入混凝土,刚度矩阵单独求解[18].桥面连续网格最小尺寸为0.03 m,其他位置网格尺寸为0.1 m,全桥模型共309 944个实体单元,6 984个杆单元.
支座采用弹簧单元(spring1),分别设置了竖向刚度K1、转动刚度K2和纵向刚度K3这3个方向弹簧约束,横向固结.弹簧刚度值通过试验得到.测试方法如下:在该桥梁板铰缝浇筑前,采用千斤顶在某一片梁板跨中按设计等效荷载加载集中力,并用千分表测试梁端上、下缘的纵向位移和支座处的竖向位移,由此推算出弹簧单元刚度取值分别为:K1=5.94×106N/m,K2=17 899 N/(°),K3=1.814×109N/m.
采用矩形刚体块模拟加载车辆轮胎,本文的货车后轴为双轮组,依据文献[19]的方法,将轮胎接地印迹简化为近似均匀分布的矩形,大小为0.23 m×0.32 m.荷载大小根据公路-II级车辆轴载计算得出,并作用于影响线最不利位置.有限元求解采用Newton-Raphson法进行迭代,考虑几何大变形.
1.3 拉杆式桥面连续
拉杆式桥面连续构造示意图如图3所示,简支梁跨中车辆荷载作用下的受力形式如图4所示.梁端上翘,直接挤压桥面连续混凝土使其受负弯矩作用,同时梁端外移,梁缝张开,使得混凝土连接钢筋受拉,如果连接钢筋与混凝土的黏结性能过大,则混凝土易被受拉钢筋拉裂.

图3 拉杆式桥面连续有限元模型Fig.3 Schematic diagram of DRLS

图4 拉杆式桥面连续受力示意图Fig.4 Schematic diagram of DRLS
1.4 拱型桥面连续
如图5所示,拱型桥面连续有限元模型,拱形钢板与混凝土之间采用Tie连接,T肋采用Embedded region的方法嵌入到桥面连续混凝土内,假设在加载过程中钢板与混凝土不发生脱离.

图5 拱型桥面连续有限元模型Fig.5 Finite element model of ALS
本文对文献[17]中的拱型桥面连续进行了2点改进,从而达到了拱顶混凝土完全受压的状态.一是增大拱的跨径,二是在分隔缝中插入薄钢板.在有限元模型中,分隔缝混凝土与钢板之间设置法相面面接触,采用Hard接触属性,接触面只传压不传拉[20].
1.4.1 拱跨对拱顶混凝土受力的影响 保持拱的矢高f不变,建立3个不同跨径的拱型桥面连续模型.其中,l为拱的跨径,d为支座纵向间距,模型M1、M2、M3分别代表l

表1 拱顶混凝土正应力
为了解释这个现象,以简支板梁跨中车辆荷载作用的梁端上翘为例,如图6所示,为M1和M3这2种跨径的拱型桥面连续随梁端转动变形示意图,图中虚线圆弧表示变形后的拱跨.从图6中可以看出,从支座中心线OD到梁端的d/2长度的梁体发生了竖直向上和水平向右的位移,支座中心线右侧的梁体发生了竖直向下和水平向右的位移.对于M1,上翘的梁端使其拱脚从B点移至B′点,产生了竖直向上的位移,导致M1桥面连续整体上拱,类似于拉杆式桥面连续受梁端上翘挤压一样,对拱顶混凝土的受压不利;当l>d(M3模型),拱脚从A点下移至A′点,M3桥面连续整体下挠,对拱顶混凝土的受压有利.

图6 拱跨与梁端位移关系的示意图Fig.6 Deformation of arched link slab with different arch spans
为了定量确定拱跨l与梁端位移Δ之间的关系,根据图6示意图,以M3为例推导拱的竖直位移ΔV和水平位移ΔL的计算公式:
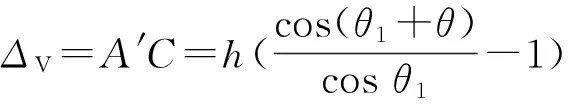
(1)
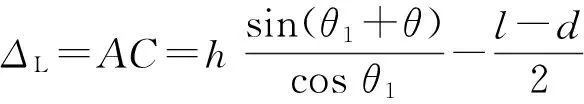
(2)

(3)
式中:θ1为按式(3)计算得出的简支板梁支座中心线与拱脚间的夹角,θ为按式(4)计算得出的简支板梁梁端转角.当主梁跨中作用集中力时,

(4)
式中:F为集中力,E为板梁的弹性模量,I为截面抗弯惯矩.偏安全的计算,考虑车辆超载情况,荷载按照公路-I车辆载重的1.5倍加载.由式(1),(3)和(4)可以得到本桥16 m跨径板梁的梁端转角为0.171°,梁端竖直向上位移为1.04 mm.令ΔV≤ 0,由式(1)和(3)得到l≥ 697 mm,与支座间距700 mm几乎一致.说明当拱跨l大于支座间距d时,拱型桥面连续在板梁跨中车辆荷载作用下将整体下挠,对拱顶混凝土的受力比较有利.
如表2所示,列出常用的4种跨径预应力混凝土1.25 m宽空心板梁的支座纵向间距和梁端转角计算值,表中L为板梁标准设计跨径.由表2可以看出,随着跨径增大,支座纵向间距、梁端竖向位移和梁端转角都相应增大,最大的20 m跨径板梁支座纵向间距为700 mm,梁端转角约为0.2°,梁端上翘约1.2 mm.说明,对于空心板梁桥,拱的跨径l只要大于700 mm,矢高f只要大于1.2 mm,就可以避免梁端上翘对桥面连续的竖向挤压作用.
表2 常用预应力混凝土空心板梁的梁端最大位移
Tab.2 Critical displacement of beam-end in common prestress concrete hollow-cored slab beam

L/md/mΔV/mmθ/(°)105000.510.116136000.870.143167001.040.171207001.190.195
但是,拱跨增大会降低拱的竖向刚度,式(5)为集中力荷载下拱顶的竖向位移,由式(5)可知,拱跨增大,拱顶的竖向位移显著增大.因此,拱跨l=700 mm是合适的.
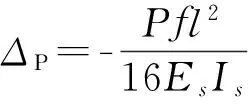
(5)
式中:Δp为拱顶的竖向位移,P为单位长度等效车轮荷载,Es为钢材弹性模量,Is为钢拱单位长度抗弯惯矩.
1.4.2 矢高对拱型桥面连续竖向刚度的影响 矢高f与拱顶正弯矩成正比,为了使拱顶产生尽量大的正弯矩,在满足最小保护层厚度的前提下,f越大越好.一般空心板梁桥桥面铺装的混凝土层厚度为100 mm,钢板的混凝土保护层厚度取40 mm,除去钢板厚度和T肋高度,得到f=30 mm.
在相同荷载下,让拱型桥面连续竖向位移与拉杆式桥面连续竖向位移相同,当l=700 mm,f=30 mm时,由式(5)可以得到拱型桥面连续所需的最小抗弯惯矩I.通过焊接T肋加强刚度来达到该I值.

图7 拱型桥面连续构造图Fig.7 Structural drawing of arched link slab
综上,如图7所示,本文得到了适合空心板梁桥的拱型桥面连续构造图.由图7可见,T肋采用5 mm厚钢板焊接,T肋间距为200 mm,拱跨1/4位置钢板上焊接间距200 mm的剪力钉.
1.4.3 分隔缝对拱顶混凝土受力的影响 浇筑桥面连续混凝土前,在分隔缝处竖向插入薄钢板,人为将桥面铺装与桥面连续的混凝土断开,切断了桥面铺装混凝土对桥面连续混凝土的拉应力传递,但能有效地传递桥面铺装对桥面连续混凝土的压应力.如图8所示,在正温度梯度荷载下,梁端下挠、梁缝间距减小,会导致拱顶负弯矩使混凝土受拉的不利情况.此时,桥面铺装传递过来的压应力发挥了作用,抵消了拉应力.由图8和表1可以看出,在正温度梯度下,拱顶混凝土为受压状态.

图8 梁端下挠对拱型桥面连续受力影响示意图Fig.8 Influence of beam-end deflection on ALS stress with hard thin steel plates in cuts
如图9所示,空心板梁桥拱型桥面连续构造的拱形钢板厚度为10 mm,拱跨为700 cm,矢高为30 mm,拱顶混凝土保护层厚度为40 mm.拱上T肋厚度为5 mm,宽40 mm,间距200 mm,拱背1/4跨径上焊接2排剪力钉;T肋之间拱脚上焊接600 mm长Φ16纵向弯起钢筋;桥面铺装与桥面连续混凝土之间埋设30 mm(厚)×50 mm(高)油浸软木条,上面嵌入2 mm(厚)×70 mm(高)钢片;拱脚下垫3 mm厚油毛毡,利于拱脚纵向滑动.

图9 空心板梁桥拱型桥面连续布置图Fig.9 Layout of arched link slab used in hollow-cored slab beam bridge
2 桥面连续荷载试验
在荷载试验中对拉杆式桥面连续混凝土上表面和连接钢筋的应变进行了测试,拱型桥面连续对拱顶混凝土上表面的应变进行测试.混凝土测点采用WS型振弦式混凝土应变计埋置于混凝土中,钢筋测点采用振弦式钢筋应变计焊接于连接钢筋上.
2.1 拉杆式桥面连续测点布置
如图10所示,B1、B2、B3为3个混凝土应力测点,在对应的无黏结滑移钢筋上也布置了3个钢筋测点S1、S2、S3.对加载过程中混凝土和无黏结钢筋的应变进行测试对比.

图10拉杆式桥面连续测点布置图Fig.10 Strain measurement points of DRLS
2.2 拱型桥面连续测点布置
如图11所示,A1~A4为4个混凝土应力测点.
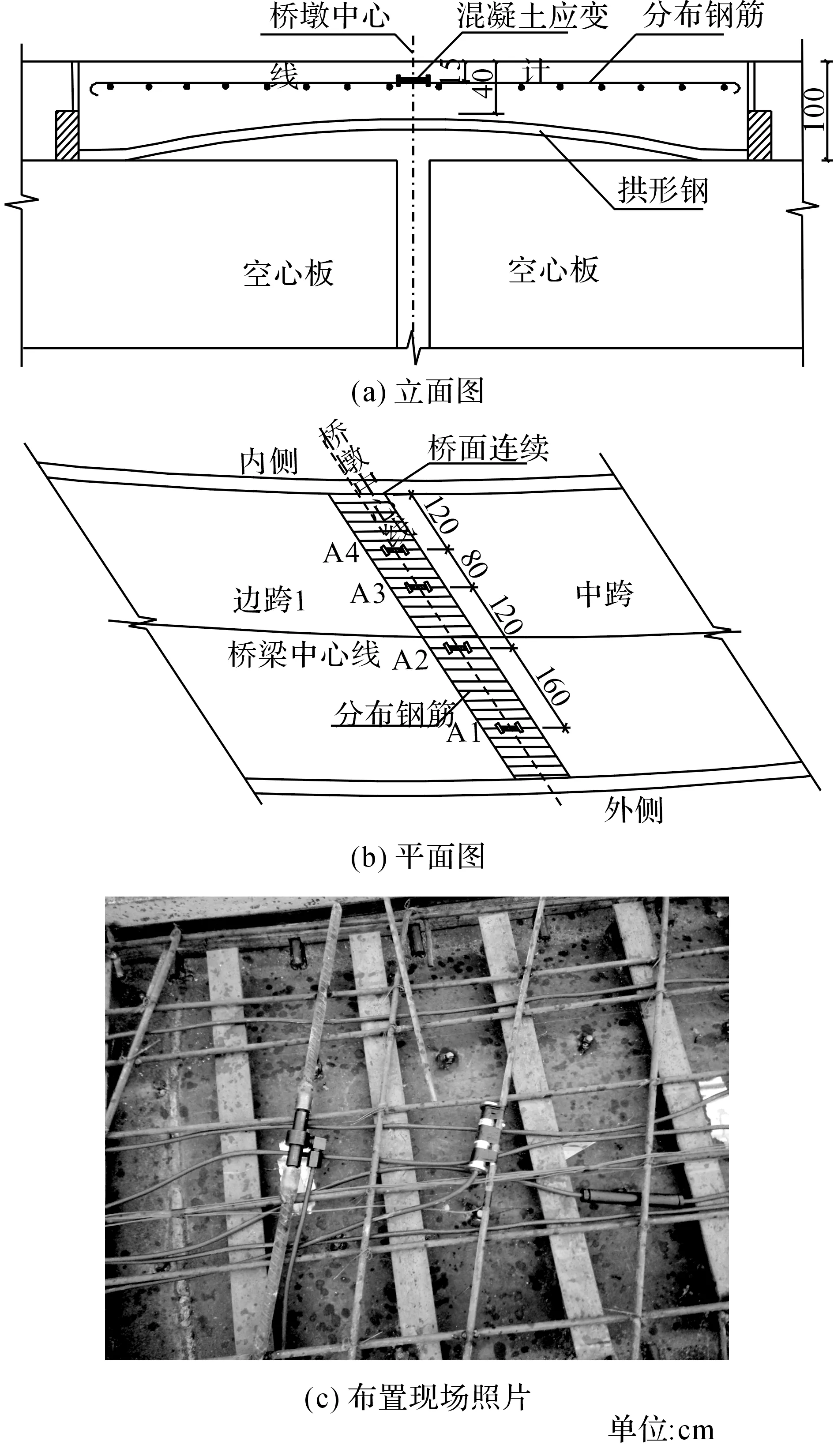
图11 拱型桥面连续测点布置图Fig.11 Strain measurement points of ALS
2.3 试验加载
采用4辆重约300 kN的货车加载,分2个工况,拱型桥面连续为工况一,拉杆式桥面连续为工况二.如图12所示,工况一的加载方式为在边跨1和中跨跨中位置各加2辆车,车尾对车尾布置,车辆中轴均加在跨中位置.工况二将边跨1的2辆车移到边跨2,其他布置形式同工况1.每个工况分4级加载,用车辆数量来控制.工况一的4级加载为1级(A车)、2级(A、B车)、3级(A-C车)和4级(全部).
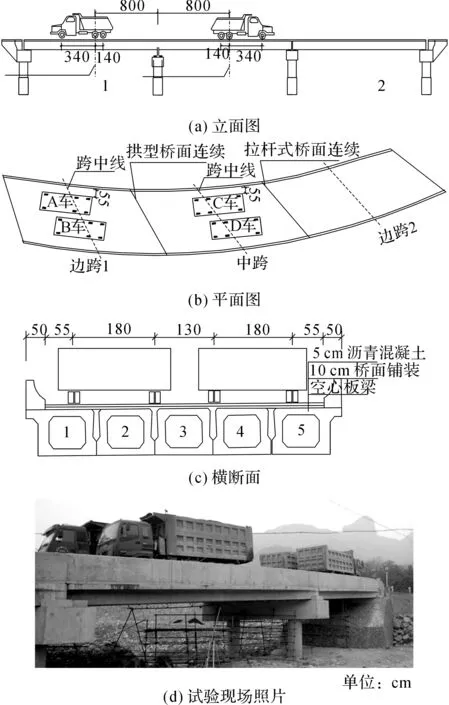
图12 试验加载示意图Fig.12 Layout of live loads
3 试验结果分析
3.1 拱型桥面连续受力分析
如表3所示为最大级荷载下拱型桥面连续试验与有限元对比结果.如图13所示,为混凝土A3点在各级荷载下的计算值与试验值对比曲线,图中N为加载级别.由表3和图13可以看出,有限元模型较好地模拟了拱型桥面连续混凝土的实际受力,随着车辆荷载增加,拱顶混凝土的压应力不断增大.
表3 最大级荷载下桥面连续混凝土的σ
Tab.3 Longitudinal stress of DRLS and ASL under max live load
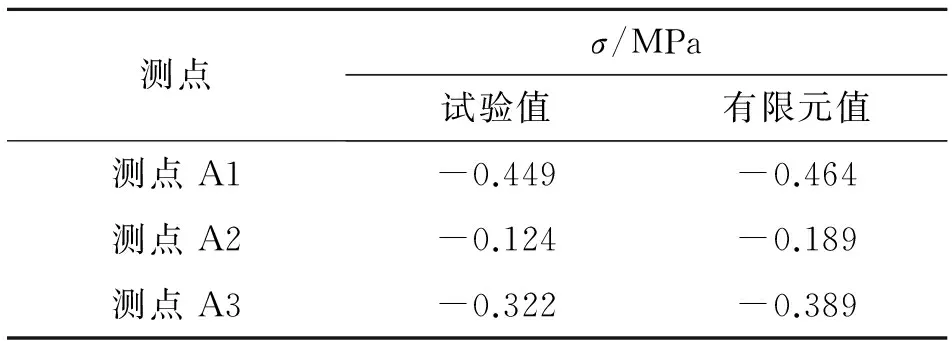
测点σ/MPa试验值有限元值测点A1-0.449-0.464测点A2-0.124-0.189测点A3-0.322-0.389
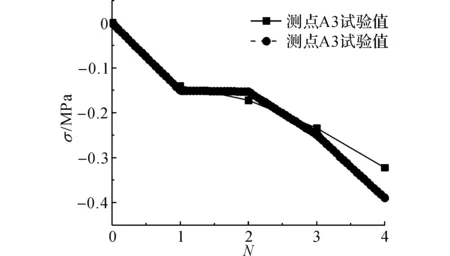
图13 拱型桥面连续应变对比曲线Fig.13 Stress curves of point A3 on ASL
3.2 2种桥面连续混凝土的应力
如图14所示,为各级荷载下拉杆式和拱型桥面连续的混凝土的应力变化结果.由图14可见,拉杆式桥面连续混凝土为拉应力,并随荷载增加而增大,最大级荷载下的拉应力约为0.6 MPa.拱型桥面连续混凝土为压应力,也随荷载增加而增大,最大级荷载下的压应力约为-0.5 MPa.试验结果表明拱型桥面连续混凝土在车辆荷载作用下完全受压,而且压应力随荷载增加而增大.由此推测,即便在超载情况下,拱型桥面连续混凝土依然能够保持受压状态,而拉杆式桥面连续混凝土可能因拉应力过大而开裂.

图14 桥面连续混凝土应力试验值Fig.14 Concrete strain on surface of DRLS and ASL under live loads
3.3 拉杆式桥面连续受力分析
为了探究拉杆式桥面连续混凝土受拉的原因,如图15所示,对实测的无黏结钢筋和混凝土的应变进行对比分析,图中,ε为正应变.由图15可以看出,随着车辆荷载增加,无黏结钢筋和混凝土的拉应变几乎同步增加,说明无黏结钢筋和混凝土之间并不是滑移的.这很有可能是施工工艺不到位所造成的,说明拉杆式桥面连续受施工工艺的要求比较苛刻,实际受力往往无法达到理想的设计效果,容易出现无黏结钢筋和混凝土同步受拉的情况.
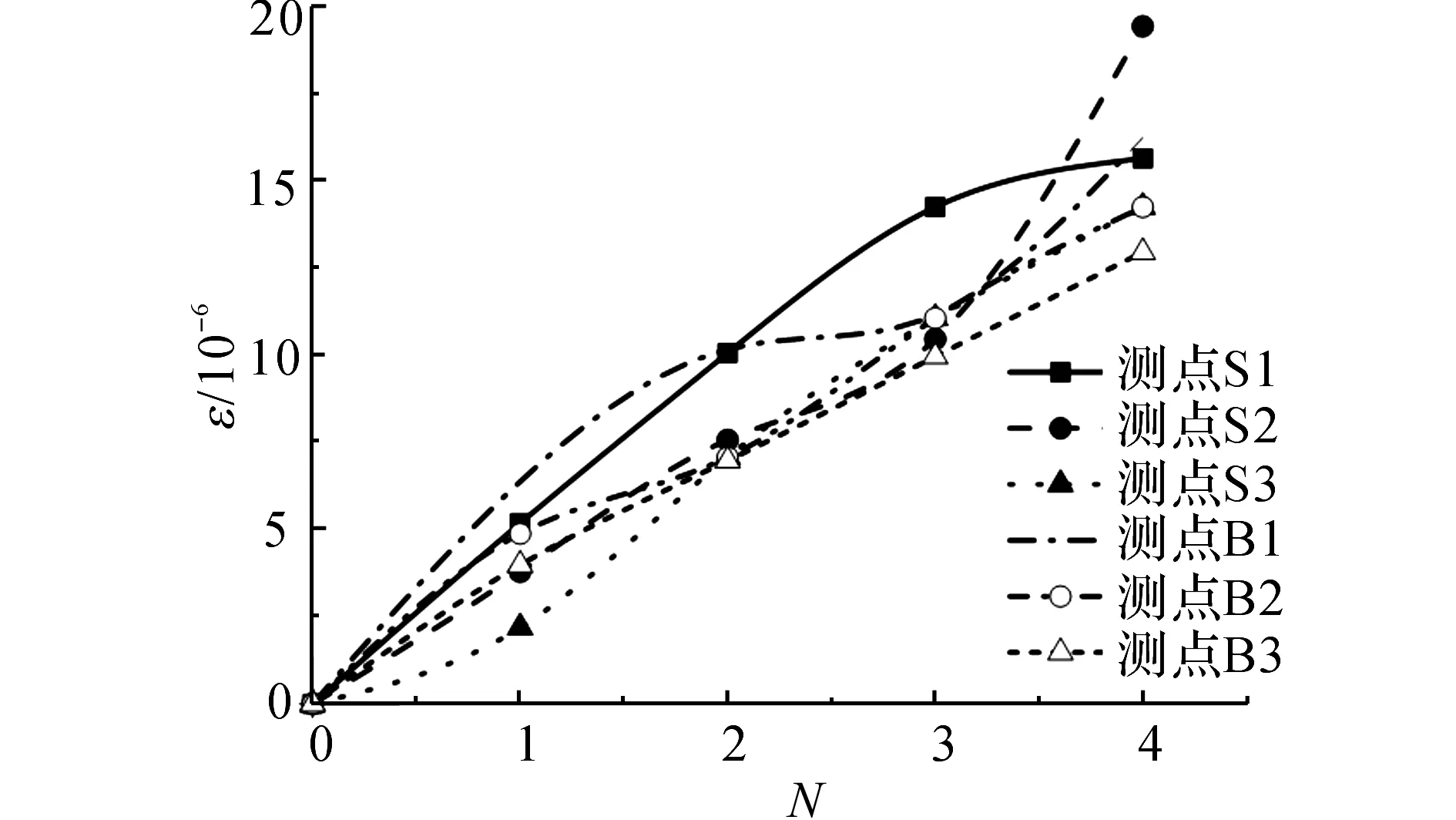
图15 拉杆式桥面连续无黏结钢筋与混凝土的应变对比Fig.15 Strain of the debonded steel and concrete of DRLS under live loads
由此建立拉杆式桥面连续的有限元模型,并假设无黏结钢筋与混凝土同步受力,如表4所示,得到最大级汽车荷载作用下桥面连续混凝土应力的计算值与试验值对比结果.由表4和图16可以看出,实际拉杆式桥面连续中,无黏结钢筋与混凝土之间滑移可忽略不计,有限元模型中采用无黏结钢筋与周围混凝土共同变形的建模方式其模拟结果能够准确反映拉杆式桥面连续的实际受力.
表4 最大级荷载下桥面连续混凝土的应力
Tab.4 Longitudinal stress of DRLS and ASL under max live load/MPa
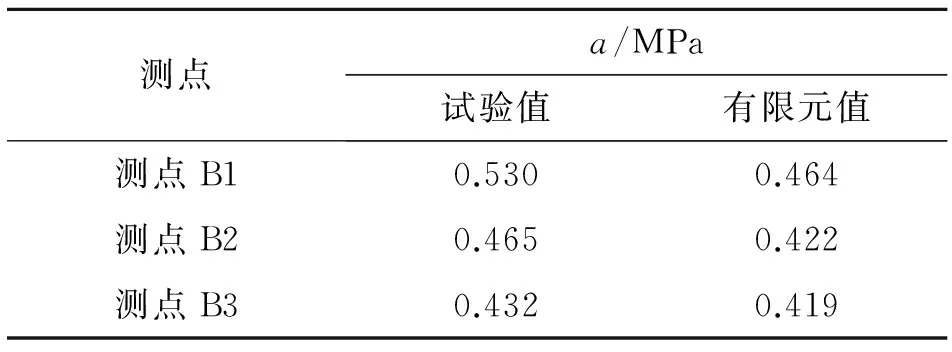
测点a/MPa试验值有限元值测点B10.5300.464测点B20.4650.422测点B30.4320.419
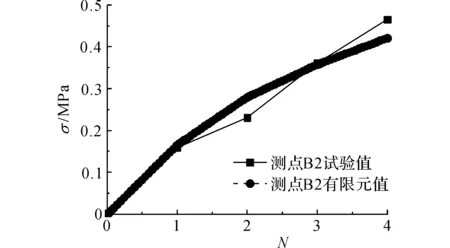
图16 拉杆式桥面连续应变对比曲线Fig.16 Stress curves of point B2 on DBSL
4 结 论
通过对拉杆式和拱型桥面连续的在空心板梁桥上的实桥试验研究和数值仿真分析对比,得到以下结论:
(1)本文给出的拱型桥面连续构造形式适用于空心板梁桥,可以在使用荷载下使得拱顶混凝土达到受压状态,为改善桥面连续混凝土开裂提供了有效途径;
(2)拉杆式桥面连续的施工工艺复杂,无黏结钢筋与混凝土很难达到理想的无黏结效果,实测发现无黏结钢筋和混凝土的拉应变几乎同步增加,这是导致使用荷载下混凝土开裂的重要原因.
[1] 温晓强.桥梁桥面连续构造设计与施工技术[J].公路交通科技:应用技术版,2013,01: 193-194.
WEN Xiao-qiang. Structure design and construction technology of bridge link slab [J]. Highway traffic technology :Application. 2013,01: 193-194.
[2] 吕筱珩.寒区简支梁桥面连续新型构造形式研究[D].哈尔滨:哈尔滨工业大学,2012.
LV Xiao-heng. Research on new construction types of the continuous deck of simple-supported girder bridge in cold region[D].Harbin: Harbin Institute Of Technology, 2012.
[3] 刘龙.预应力混凝土简支梁桥桥面连续结构行为研究[D].成都:西南交通大学,2014.
LIU Long. Study on the continuous deck’ s behavior of simply supported prestressed concrete beam bridge [D]. Chengdu: Southwest Jiaotong University, 2014.
[4] 钟俊飞.简支体系桥面连续病害防治技术研究[D].哈尔滨:哈尔滨工业大学,2014.
ZHONG Jun-fei. Research on disease prevention and control technology of simple-supported system with continuous deck [D].Harbin: Harbin Institute Of Technology, 2014.
[5] 苏龙,杨絮,胡章立.空心板桥病害剖析及桥面连续结构整治对策[J].公路交通技术,2011(2): 100-103.
SU Long, YANG Xu, HU Zhang-li. Analysis for diseases of hollow slab bridges and remediation countermeasures for continuous structures on Deck[J]. Technology of Highway and Transport, 2011(2): 100-103.
[6] LI V C, FISCHER G, KIM Y, et al. Durable link slabs for jointless bridge decks based on strain-hardening cementitious composites[R]. Michigan: Michigan Department of Transportation, 2003.
[7] AYMAN M. OKEIL, ADEL ElSafty. Partial continuity in bridge girders with jointless decks [J]. Practice Periodical on Structural Design and Construction, 2005,10(4):229-238.
[8] 沈青川.简支梁桥桥面连续构造性能比较研究[D].长沙:中南大学, 2011.
SHEN Qin-chuan. Study on performance of continuous deck structure in simple-supported beam bridge [D]. Changsha: Central south University, 2011.
[9] 丁勇,黄奇,黄剑源.连续桥面简支梁桥静动力特性的理论分析方法研究[J].工程力学,2015, 32(9): 100-110.
DING Yong, HUANG Qi, HUANG Jian-yuan. Theoretical analysis for static and dynamic characteristics of multi-simple-span bridge with continuous deck [J]. Engineering Mechanics, 2015, 32(9): 100-110.
[10] WING K M, KOWALSKY M J. Behavior, analysis, and design of an instrumented link slab bridge [J]. Journal of Bridge Engineering, 2005, 10(3): 331-344.
[11] ULKU E, ATTANAYAKE U, AKTAN H. Jointless bridge deck with link slabs: design for durability [J]. Transportation Research Record: Journal of the Transportation Research Board, 2009: 68-78.
[12] AUA, LAMC, AUJ,et al.Eliminating deck joints using debonded link slabs: research and field tests in ontario [J]. Journal of Bridge Engineering, 2013,18(8): 768-778.
[13] 潘志炎,茅兆祥,刘敏,等.简支梁桥面连续构造的有限元分析与改进[J].公路交通科技,2010.27(4): 89-94.
PAN Zhi-yan, MAO Zhao-xiang, LIU Min, et al. Finite element analysis and improvement of continuous slab deck of simple supported beam bridge [J]. Journal of Highway and Transportation Research and Development, 2010,27(4): 89-94.
[14] QIAN S, LEPECH M D, KIM Y Y, et al. Introduction of transition zone design for bridge deck link slabs using ductile concrete [J]. ACI Structural Journal, 2009, 106(1): 96-105.
[15] SABER A, ALETER A R. Behavior of FRP link slabs in jointless bridge decks [J]. Advances in Civil Engineering. 2012(3): 109-118.
[16] 赵成栋.一种新型PBL桥面连续构造的设计[J].中国市政工程,2014(6): 27-29.
ZHAO Cheng-dong, A Design of a new deck continuous structure with PBL [J]. China Municipal Engineering, 2014(6): 27-29.
[17] 王岗,谢旭,王城泉,等.简支梁桥拱型桥面连续构造的受力性能[J].浙江大学学报:工学版,2014,48(4): 1049-1057.
WANG Gang, XIE Xu, WANG Cheng-quan, et al. Mechanical performance of arclrtype continuous slab-deck on simply-supported birder bride [J]. Journal of Zhejiang University: Engineering Science,2014, 48(4): 1049-1057.
[18] 庄茁,张帆,岑松,等.ABAQUS非线性有限元分析与实例[M].北京:科学出版社,2005. 314-317.
[19] JTGD60-2004.公路桥涵设计通用规范[S].北京:中国建筑工业出版社,2014.
JTGD60-2004. General code of design of highway bridges and culverts[S].Beijing: China architecture﹠building press, 2014. 23-25.
Field tests on mechanical characteristic of link slab on hollow-cored slab beam bridge
WANG Cheng-quan, SHEN Yong-gang, WANG Gang, XIE Xu
(DepartmentofCivilEngineering,ZhejiangUniversity,Hangzhou310058,China)
The arched link slab on hollow-cored slab beam bridge was proposed to solve the problem that the existed bridge link deck structure is liable to fracture and water seepage. The numerical simulation was modeled to analyze the mechanical characteristic of arched link slab. The proper parameters of the arch span and the arch rise were obtained through theory deduction and numerical calculation. Under the action of vehicle load or negative temperature gradient conditions, the tensile stress was delivered from the link slab to the arch by the longitudinal forced rebars, which produced positive moments and compression on the concrete of arch crown. Under the temperature variation of positive gradient, the pressure force was delivered from the link slab to the arch by the longitudinal forced rebars, which produced negative moments and tensile stress on arch crown. The pressure stress on link slab can be transmitted to the arched link slab through the thin steel plates in the seams to keep the arch crown concrete in compression. The effectiveness of the arched link slab was verified by bridge field tests. The results of experiment and finite element analysis show that the concrete of arched link slab is always in compression under the vehicle load and temperature variation, but the poor slip effect between the debonded reinforced steel bars and the concrete is the main cause of the existed debonded rebar link slub fractured.
hollow-cored slab beam bridge; arched link slab; debonded rebar link slab; mechanical characteristic; field test
2015-06-15.
浙江省自然科学基金资助项目(LY16E080006);公路中小桥梁病害分析及维修策略研究资助项目(2009H37).
王城泉(1989),男,博士生.从事桥梁结构研究:ORCID: 0000-0003-0738-7829. E-mail: wcqdesign@163.com
申永刚,讲师.ORCID: 0000-0002-8508-8296. E-mail: sygdesign@zju.edu.cn
10.3785/j.issn.1008-973X.2016.08.003
U 448
A
1008-973X(2016)08-1438-08
浙江大学学报(工学版)网址: www.journals.zju.edu.cn/eng
