对称布置2根单侧加劲肋的有效刚度

杨 章, 童根树, 张 磊

(浙江大学 土木工程学系,浙江 杭州 310058)



对称布置2根单侧加劲肋的有效刚度

杨 章, 童根树, 张 磊

(浙江大学 土木工程学系,浙江 杭州 310058)

针对对称布置2根单侧加劲肋的加劲板在单轴受压屈曲分析中的有效刚度问题.用隔离体分析法,分别对加劲肋和被加劲板进行二阶分析,考虑加劲肋自由扭转、约束扭转和剪切变形的影响,通过板和加劲肋在连接处的位移协调条件,得到3种屈曲模态下加劲板的屈曲方程和加劲板参与加劲肋工作的有效宽度解析表达式,获得对称布置2根单侧加劲肋的有效扭转刚度和有效抗弯刚度的表达式,相比于布置一根加劲肋的加劲板的结果,两者有较大不同.与有限元模拟结果进行分析比对表明,获得的有效刚度公式具有良好精度,适用于任意开口和闭口截面的单侧加劲肋板.

对称布置；屈曲模态；2根单侧加劲肋；有效刚度；有效宽度

加劲板被广泛应用于桥梁、航空器、船舶、建筑等领域,钢桥中的箱梁结构、飞机的机翼.船体的甲板和建筑中的钢板剪力墙、组合梁等都是典型的薄壁加劲结构.薄板是钢结构中重要的受压、受弯和受剪构件,如T形、工字形和箱形梁中的组成板件、剪力墙钢板等.薄板具有一定的面外抗弯能力,但这种能力很大程度上依赖于边界支承条件.相比较于增加薄板厚度的做法,在薄板上设置加劲肋能够更有效地提高薄板的面外抗弯刚度,从而大大提高薄板的承载力.单侧加劲板是一种更高效、适用范围更广的加劲结构.高层民用建筑钢结构设计规程建议加劲钢板剪力墙采用单侧加劲肋[1].童根树等[2-3]对布置一根单侧加劲肋时,加劲肋的有效抗弯刚度进行了分析,得到了布置一根单侧加劲肋时的加劲肋有效刚度计算公式.而在实际的加劲钢板剪力墙中往往纵向布置多根加劲肋.当布置多根单侧加劲肋时,对于每根单侧加劲肋的有效扭转常数和有效宽度的计算能否采用一根单侧加劲肋模型获得的结果是不确定的.陶文登[4]采用有限元方法对布置多根加劲肋的钢板剪力墙进行屈曲分析,给出加劲肋门槛刚度和加劲肋抗弯刚度、扭转刚度以及布置方式的关系,并给出了单侧加劲肋和双侧加劲肋的拟合公式.本文将通过对称布置2根单侧加劲肋的加劲板进行屈曲分析,研究不同的加劲肋数量、加劲肋布置间距、布置方式和屈曲模态时单侧加劲肋的有效扭转刚度和有效抗弯刚度的表达式,从而将双侧对称加劲肋和单侧加劲肋的计算方法相统一.

1 单侧加劲钢板的轴压弹性屈曲

双加劲肋的最常见布置方式就是关于钢板中线对称布置,本文主要对这种对称布置2根单侧加劲肋的钢板进行轴压屈曲分析.加劲板分析模型如图1所示,长度为a,宽度为b,四边简支,2根纵向加劲肋形心轴到钢板中线的距离均为ηb,η为加劲肋偏置系数,加劲肋两端简支,钢板和加劲肋两端施加轴压应力σp.在单轴受压下,加劲板可能发生的横向屈曲模态有3种,如图2所示,分别是横向(y轴方向)1、2、3个半波.而在纵向,加劲板在压力作用下发生失稳非常接近于多个正弦波形.

图1 加劲板模型Fig.1 Stiffened plates

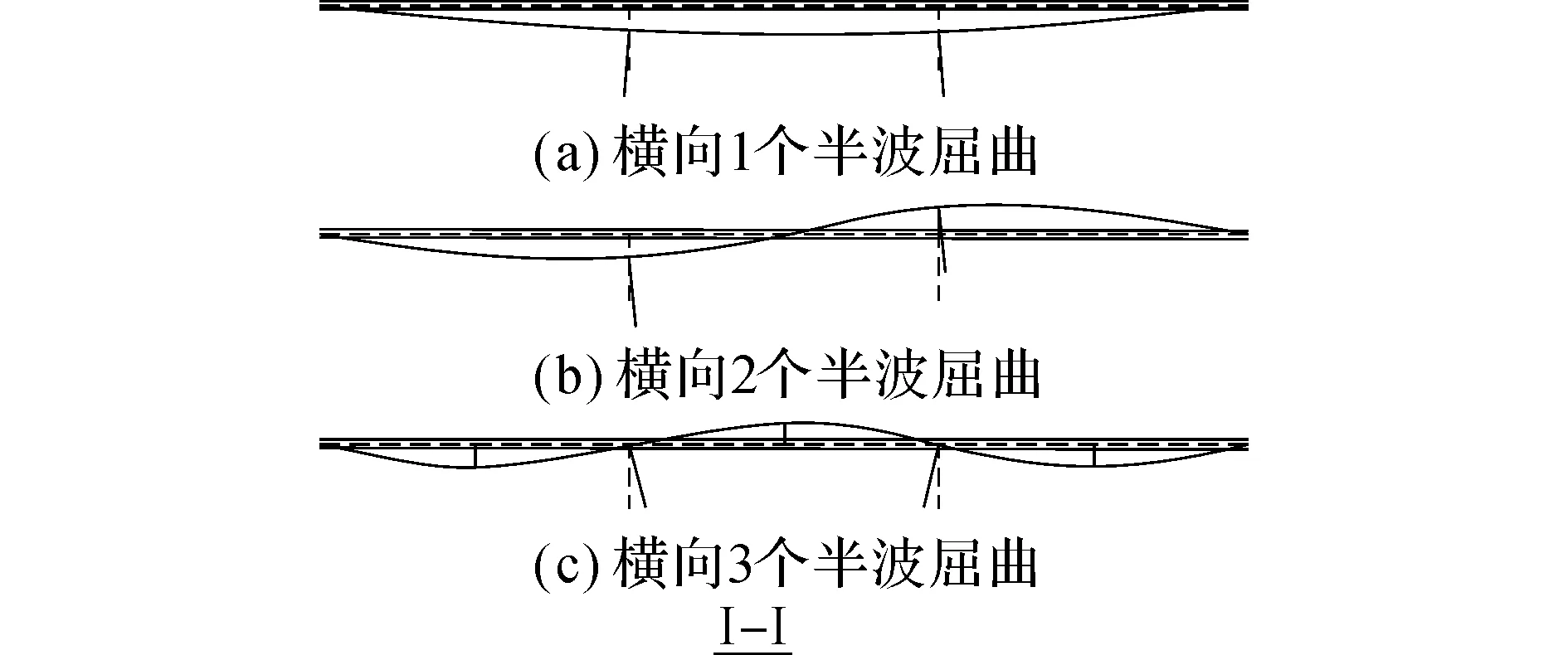
图2 横向屈曲模态Fig.2 Lateral buckling modes

可设加劲板整体屈曲面外挠度函数为

(1)

式中：Ym为钢板挠度的横向形函数.m为加劲板纵向屈曲半波数.

常用的加劲肋截面类型如图3所示,hs为加劲肋高度,be为有效宽度.

图3 加劲肋截面Fig.3 Sections of stiffener

本文分析的加劲肋和钢板材料均为钢材,钢材由于其材料性能相对较为均匀,采用如下弹性分析的假定：

1)钢板和加劲肋假定为各向同性的理想弹性材料

2)钢板和加劲肋是刚性连接,即连接处各点应力应变相同,连接的板件之间没有相对转角

3)钢板采用薄板的弹性理论

4)加劲肋按照简支梁分析,根据Timoshenko梁理论计算其剪切变形

5)分析的是结构小变形弹性阶段性能

2 横向一个半波屈曲

图4 模态1,开口加劲肋隔离分析Fig.4 Mode 1,isolated analysis of open stiffeners

图5 模态1,开口加劲肋隔离分析Fig.5 Mode 1,isolated analysis of closed stiffeners

先对横向一个半波的屈曲模态进行分析,用隔离体分析法.对称性可知2根加劲肋的应力应变相同.开口加劲肋只有一条连接线(加劲肋和钢板的连接部分),如图4所示,Fsz为加劲肋和钢板之间z轴方向相互作用力,Fsx为加劲肋和钢板之间x轴方向相互作用力,Fsy为加劲肋和钢板之间y轴方向相互作用力,Ms为加劲肋和钢板之间相互扭矩.闭口加劲肋和钢板有2条连接线,为了和开口加劲肋相统一,如图5所示为槽型加劲肋两腹板上受到的作用力相同,加劲肋对钢板的作用力合并作用在2根连接线的中线上,钢板对加劲肋的扭矩的作用方式是作用在闭口截面(槽型加劲肋和板肋连接线之间的钢板组成的闭口截面)的加劲肋上.

2.1 加劲肋弯扭分析

对加劲肋进行分析时(如图6所示)采用Timoshenko梁理论,考虑剪切变形.加劲肋两端受均布压应力σp,hc为加劲肋形心到板中面距离,hss为加劲肋剪切中心到加劲板中面距离,vs为加劲肋剪切中心的y轴方向位移,θs为加劲肋的扭转角.加劲肋跟随加劲板一起屈曲,加劲肋的面外挠度函数为

(2)

图6 加劲肋弯扭分析Fig.6 Stiffener analysis of bending and torsion

可推知,加劲肋受到的z轴方向力Fsz为正弦函数分布：

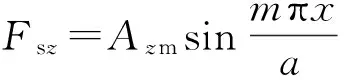
(3)

x轴方向力Fsx则是余弦分布：

(4)

式中:Azm和Axm为待定常系数.

Fsz产生的对形心轴的弯矩为

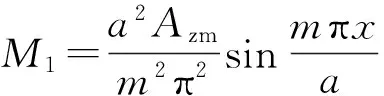
(5)

Fsx产生的对加劲肋自身形心轴的弯矩和形心处等效轴力为

(6)

(7)

轴压应力σp产生的二阶弯矩为

M3=σpAsws.

(8)

1.1.1 加劲肋Z轴方向剪切变形 按照Timoshenko梁理论,剪切变形不引起纵向位移,纵向位移由弯曲变形引起[5],且有如下关系：

(9)

式中:γs为加劲肋剪切变形引起的截面转角.

且加劲肋截面转角γs和加劲肋截面剪力Qs之间关系[5]为

(10)

式中:Gs为加劲肋材料的剪切模量,ks为加劲肋等效截面剪切系数,是和加劲肋中和轴位置相关的量.

加劲肋的截面剪力Qs可由Fsz分布形式求得

(11)

把式(11)代入(9)、(10)可求得加劲肋剪切变形：

(12)

1.1.2 加劲肋Z轴弯曲变形 记加劲肋绕截面形心y轴的惯性矩为Is,则加劲肋的弯曲平衡方程为

(13)

式中:Es为加劲肋的材料弹性模量.

把式(5)、(6)、(7)、(8)、(12)代入式(13)可以求得加劲肋z轴弯曲变形：

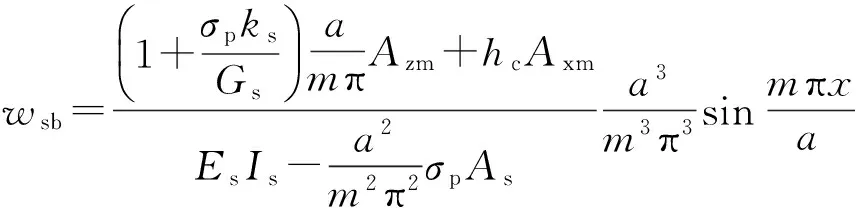
(14)

1.1.3 加劲肋z轴方向总挠度和上翼缘x轴向应变 加劲肋z轴方向总挠度ws为弯曲变形和剪切变形之和：

ws=wsb+wst.

(15)

把式(10)和式(14)代入式(15)可求得

(16)

式中:φ为剪切变形影响系数,其表达式为

(17)

由于timoshenko梁理论中剪切变形不产生纵向变形,加劲肋上翼缘的x轴方向应变εsx,top为

(18)

1.1.4 加劲肋y轴方向弯曲平衡θs按照右手螺旋法则,以大拇指指向坐标正方向为正,并假定加劲肋和钢板刚性连接,则

同时,假定加劲肋变形满足刚周边假定,则加劲肋剪切中心处的y轴方向位移为

vs=-hssθs.

(20)

y轴方向的弯曲平衡的程为

(21)

式中:Isz为截面绕形心z轴的惯性矩,y0=hss-hc.

则由式(19)、(20)、(21)可得到Fsy表达式：

(22)

其中,

(23)

图7 闭口加劲肋计算截面取用 Fig.7 Calculation area of closed stiffeners

1.1.5 加劲肋扭转平衡 在对加劲肋进行扭转分析的时,闭口加劲肋的计算截面选取和z轴方向弯曲分析时的截面选取不同.如图7所示,闭口加劲肋在抗弯计算时,Is和As的计算截面为图7(a)的槽型截面,而在扭转分析时,需要以图7(b)的封闭截面作为计算截面.

以截面(闭口加劲肋为封闭截面)剪切中心建立扭转平衡方程为

(24)

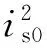
由式(22)、(23)、(24)可得ms表达式：

(25)

其中,

(26)

式中:μs为加劲肋材料泊松比.

2.2 钢板的平面应力分析

当单侧加劲板发生弯曲屈曲时,板的面内刚度会参与加劲肋抗弯工作,本节对这种作用进行分析.在弹性小变形假定下,母板中面的应力和应变按照平面应力问题求解.相当于平板在2条连接线处受到加劲肋对钢板的平面内作用力.如图8所示,采用叠加原理,布置2根加劲肋的钢板中面应力应变等于2根加劲肋单独作用时在钢板中面产生的应力和应变的叠加.

图8 模态1,板中面平面应力叠加Fig.8 Mode 1,Plane stress superposition of plate

图8中最右侧钢板只受到一根加劲肋作用力的平面应力问题已在文献[2]给出了具体求解过程,直接引用其结果可得在y=ηb.处布置一根加劲肋时,钢板中面在连接线(y=ηb.)处的纵向应变为

(27)

式中:E为钢板弹性模量,t为钢板厚度,ζ1和ζ2为一根加劲肋时钢板面内柔度系数,其表达式为

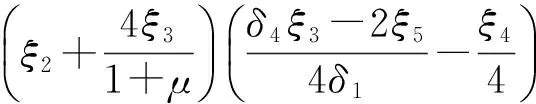
(28)

(29)

其中,μ为钢板材料泊松比,

(30)

(31)

(32)

(33)

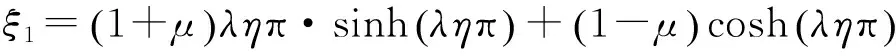
(34)

(35)

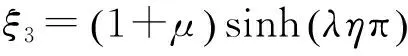
(36)

(37)

(38)

(39)

(40)

根据对称性,式(40)可变为

(41)

可求得

(42)

式中:ζ′1,1,ζ′2,1为横向一个半波时2根加劲肋的钢板面内柔度系数,其表达式为

(43)

(44)

2.3 加劲板和加劲肋变形协调条件

钢板与加劲肋在连接处纵向应变和面外挠度相同,即

ws=wy=ηb.

(45)

(46)

把式(1)、(16)、(18)、(42)代入(45)、(46)可求得Azm为

(47)

式中:

(48)

(49)

Azm代表了Fsz的大小,则由式(47)可知：Fsz由2部分组成.第1部分是与加劲肋z轴方向弯曲变形相平衡的力.第2部分是加劲肋y轴方向力Fsy通过板中面内力平衡产生的力,其值相比较于第1部分是非常小的,为最终结果便于工程应用我们忽略第2部分的效应,Azm可简化为

(50)

把式(50)代入(45)、(46)可求得

(51)

2.4 板的对称屈曲分析

横向一个半波屈曲,由对称性可取用加劲板中线右边对称半板分析,如图9所示,中线处满足横向位移为零、转角为零的边界条件.在板肋连接线处受到加劲肋作用于钢板的的面外荷载Fsz和弯矩ms,在2条加载边上有轴压应力σp.右半板被连接线分为板1和板2.则板1和板2的面外挠度wi,满足小挠度弯曲平衡方程：

(52)

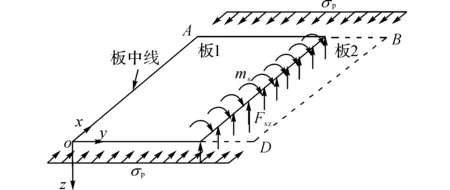
图9 钢板弯曲分析Fig.9 Bending analysis of bending

Yim=Picoshβy+Qisinhβy+Micosγy+

Nisinγy.

(53)

式中:Pi,Qi,Mi,Ni为待定系数,

(54)

(55)

则板件的y方向弯矩Miy为

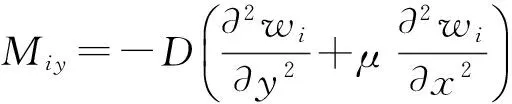
(56)

板件垂直y轴的面的竖向分布剪力为

(57)

2)在y=b/2处：

3)在y=ηb处：

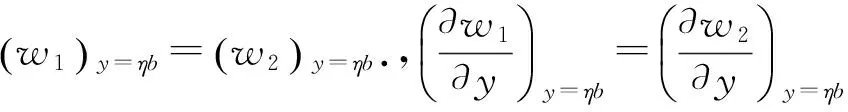
由边界条件可获得加劲板发生横向一个半波屈曲时的无量纲化屈曲方程为

f1(K)+ϑ1f2(K)+ϑ2f3(K)+ϑ1ϑ2f4(K)=0.

(58)

(59)

(60)

f1(K)=

(61)

(62)

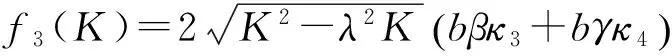
(63)

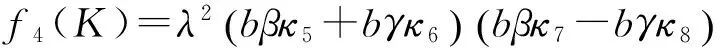
(64)

式中：

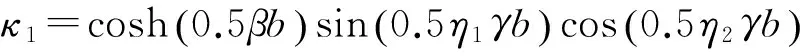
(65)

(66)

(67)

(68)

(69)

(70)

(71)

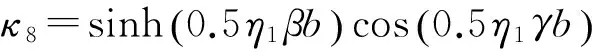
(72)

η1=0.75-η.

(73)

η2=0.25+η.

(74)

式(58)给出了单侧加劲板横向一个半波屈曲时的屈曲方程.当2根单侧加劲肋换成轴心加劲肋时,即布置2根轴心加劲肋的钢板,其横向一个半波屈曲时的屈曲方程和式(58)非常相似,只要在式(59)、(60)中用Is和Js代替Is,eff和Js,eff即可.表明：通过本文给出的有效抗弯惯性矩Is,eff解析式(式(48))和有效扭转常数Js,eff解析式(式(26)),就可以把单侧加劲问题转化为轴心加劲问题.

受压单侧加劲板发生弯曲屈曲时,加劲肋的中和轴,既不在板件的中面,也不通过加劲肋的形心,记中和轴距离板中面的距离为he,由中和轴轴向应力为零可得

(75)

把式(7)、(14)代入(75)可求得he为

(76)

从式(76)可以看出,如果E/Es=1.,加劲肋中和轴的位置刚好为加劲肋和宽度为bc的母板组成的新截面的形心,即有钢板有效宽度为bc：

(77)

把式(76)(77)代入式(48)得Is,eff关于he的表达式：

(78)

式(78)表明有效抗弯惯性矩就等于加劲肋和宽度为be母板组成的新截面的的惯性矩,而且新的截面形心轴刚好是中和轴,可以称这个新的截面为单侧加劲肋的有效截面.其中闭口加劲肋的有效截面为槽型截面和有效宽度板件组成的截面.即单侧加劲肋的有效宽度为be,be大小主要是由钢板面内柔度系数ζ′1,1决定.

3 横向2个半波屈曲

3.1 加劲肋的弯扭分析

如图10所示为加劲板发生横向2个半波屈曲,加劲肋的受力分析和屈曲模态1(横向一个半波屈曲)是相同的,只是在2个加劲肋的位移正负相反并且扭矩方向相反,即另一个加劲肋的挠度是-wsb-wst,扭矩为-ms.产生坐标正方向挠度的加劲肋的挠度和应变表达式同式(16)、(18).扭转分析也相同,加劲肋的等效扭转刚度表达式同式(26).

图10 模态2,开口加劲肋隔离分析Fig.10 Mode 2,isolated analysis of closed stiffeners

3.2 板的平面应力分析

当加劲板发生横向2个半波屈曲时,板的平面应力分析同样采用叠加原理.和屈曲模态1相比,2个半波屈曲时,2根加劲肋作用在板上的力是反对称的,即大小相同方向相反.故而叠加后的平面应变表达式为

(79)

由于对称性式(79)又可变为

(80)

可求得

(81)

式中:横向2个半波屈曲时钢板面内柔度系数ζ′1,2,ζ′2,2表达式变为

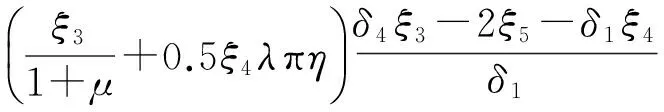
(82)

(83)

横向2个半波屈曲时有效宽度为

(84)

3.3 加劲板和加劲肋变形协调条件

加劲板发生横向2个半波屈曲时,加劲肋和钢板同样在连接线处满足位移协调条件.发生坐标正方向挠度的加劲肋的结果同一个半波相同,可获得Axm和Azm表达式同式(50)、(51),另一根加劲肋则所受力大小相同方向相反.

3.4 板的反对称屈曲分析

同样,在横向2个半波屈曲时,采用等效抗弯刚度和等效扭转刚度即可把单侧加劲问题转化为轴心加劲问题.对于单侧加劲钢板,屈曲模态2和屈曲模态1相比,有效扭转常数表达式和大小都不变为式(26),有效抗弯惯性矩表达式不变为式(48),但大小发生了变化：由于钢板面内柔度系数的不同导致有效宽度be不同,有效抗弯惯性矩Is,eff也不同.

4 横向3个半波屈曲

横向3个半波屈曲,即加劲板局部屈曲,相当于加劲肋被分割成3个非加劲板单独发生屈曲,参考文献[6]中已给出弹性约束边界条件下板件的屈曲方程表达式,

βb1sinhβb1]+γb1sinhβb1(k2cosγb1-γbsinγb1)-

βb1sinγb1(k2coshβb1+βb1sinhβb1)=0.

(85)

(86)

(87)

(88)

决定局部屈曲的屈曲系数的是单侧加劲肋的有效扭转刚度分配给两边板件的比例.若设定分配比例为：δ和1-δ.

则可知对于两边板件有

对于中间板件有

把上述的边界条件代入式(85),由屈曲应力相同,即可求得δ和屈曲系数K.

在实际情况中,加劲肋即便抗弯刚度非常大,仍旧会产生微小的竖向位移,所以和前面使用的挠度为零的弹性约束边界条件有所差别,而为了工程应用方便,可以通过给定一定的分配比例δ使其结果在偏于安全范围,直接对两边局部板件屈曲分析,则屈曲方程为

(89)

5 单侧加劲肋数量、间距和屈曲模态对有效宽度的影响

为便于比较,可把布置1根和2根单侧加劲肋钢板的有效宽度公式统一为

(90)

式中:ζ1即钢板面内柔度系数,一根时取值为式(28), 2根横向一个半波屈曲时取值为式(43),2根横向一个半波屈曲时取值为式(82).

当加劲钢板尺寸给定时,决定加劲肋有效宽度be大小的是系数ζ1,布置1根加劲肋的钢板和布置2根加劲肋的钢板的ζ1表达式是不同的；而布置两根加劲肋的钢板,屈曲模态不同时ζ1表达式也是不同的.ζ1受加劲肋数量、加劲肋间距、屈曲模态、钢板纵向弯曲半波长宽比和材料性能的影响.

图11 模态1,系数ζ1变化Fig.11 Mode1,change of ζ1

如图11所示给出了横向一个半波屈曲时,不同加劲肋布置方式,系数ζ1和板半波长宽比λ的关系.可以看出布置2根加劲肋的钢板的ζ1大于布置1根加劲肋的钢板的ζ1,由式(90)可知：在横向一个半波屈曲时,布置2根加劲肋时的be小于布置1根加劲肋时的be

如图12所示给出了横向2个半波屈曲时,不同加劲肋布置方式,系数ζ1和板半波长宽比λ的关系.可以看出布置2根加劲肋的钢板的ζ1大于布置1根加劲肋的钢板的ζ1.由式(90)可知：横向2个半波屈曲时,布置2根加劲肋时的be大于布置1根加劲肋时的be.

图12 模态2,系数ζ1变化Fig.12 Mode2,change of ζ1

如图13所示单侧加劲钢板纵向屈曲半波长宽比为1.当发生横向一个半波屈曲时,4种加劲肋布置方式的有效宽度.

图13 模态1,纵向一个半波有效宽度的变化Fig.13 Mode1,difference of effective width with one half-wave

从本文分析可以看出有效宽度由加劲板挠度的纵向形函数决定,对于承受面外荷载发生纵向正弦波形弯曲的加劲板其有效宽度可以直接采用本文的有效宽度表达式,对于其他的形函数的弯曲变形则需通过傅里叶转换求解.

在民用建筑中,楼板采用9 m×9 m或类似接近方形的楼板区隔最为常见,区隔内设置2根次梁,混凝土楼板参与次梁工作的有效宽度,与本文研究的问题非常接近,仅仅是次梁承受均布荷载,而不是正弦分布荷载,基本可以按照横向一个半波的结果应用.设λ=1等间距布置次梁,即η=1/6,此时ζ1=1.088,be=0.292 6a,比仅跨中一道次梁时的be=0.349 5a小16.3%.同样组合梁中翼缘有效宽度的取值,按照布置一根钢梁模型分析获得的有效宽度大于布置多根钢梁模型的有效宽度,偏于不安全.

6 ANSYS结果比对

采用ANSYS有限元软件进行数值分析,然后和理论值相比对,由此来验证理论结果的合理性.限于篇幅,ANSYS比对模型选用常见的板条,T型和槽型闭口加劲肋.板和肋均采用shell63单元,Es=E=2×105MPa,μs=μ=0.3,约束母板四边和加劲肋两端z向位移,约束母板形心处x方向位移,板肋连接线两端点y方向位移,在加劲板和加劲肋两端施加均布节点荷载σx.由式(56)和式(76)求得不同屈曲模态下的屈曲系数K理论值,与ANSYS结果进行比对.

如图14、15、16分别为板条加劲肋，T型加劲肋，闭口加劲肋的理论结果和有限元值结果比对数据图，

图14 η=1/6板条加劲肋结果比对Fig.14 η=1/6 comparison of plate-strip Stiffeners

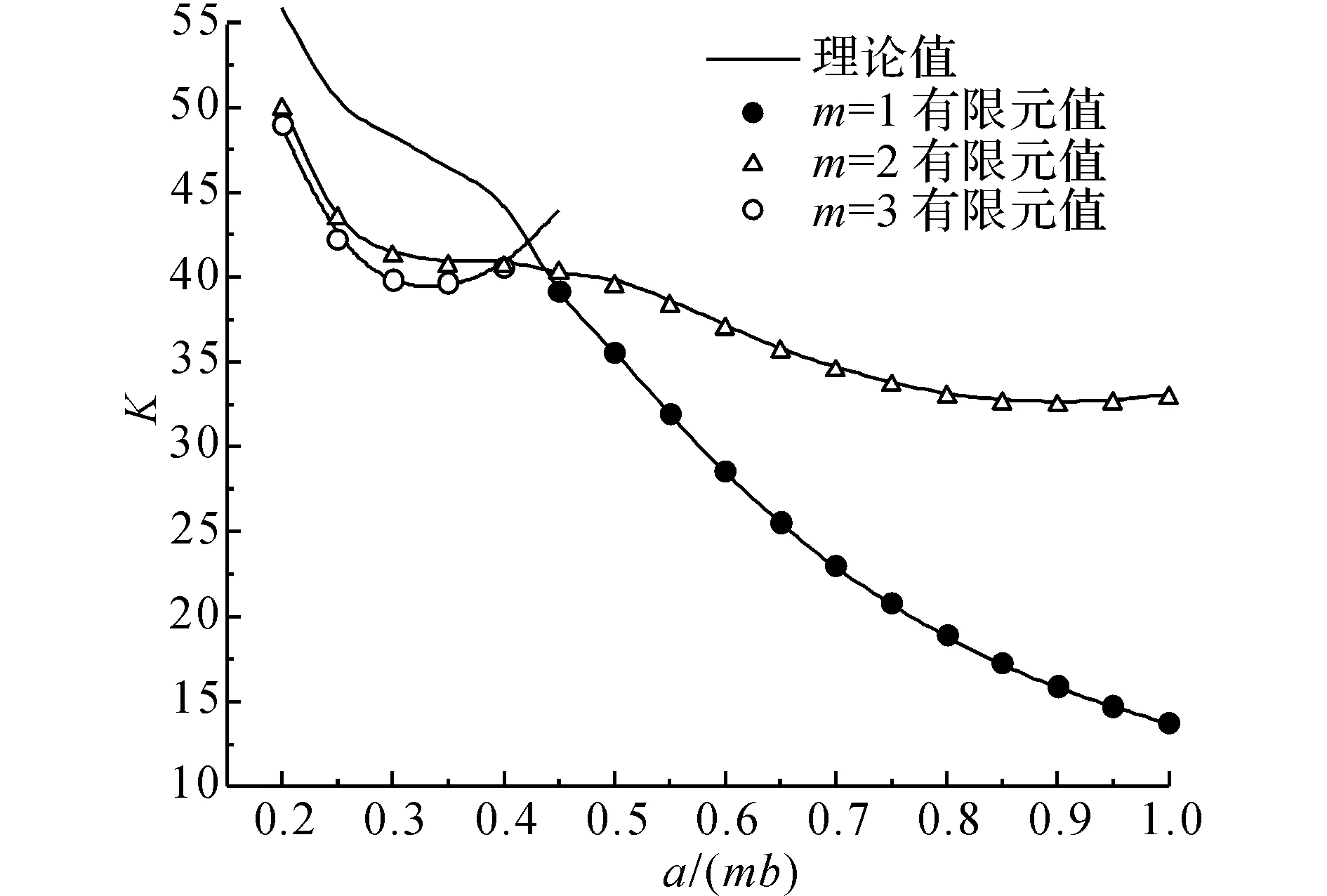
图15 η=1/6 T型加劲肋结果比对Fig.15 η=1/6 comparison of T-Stiffener

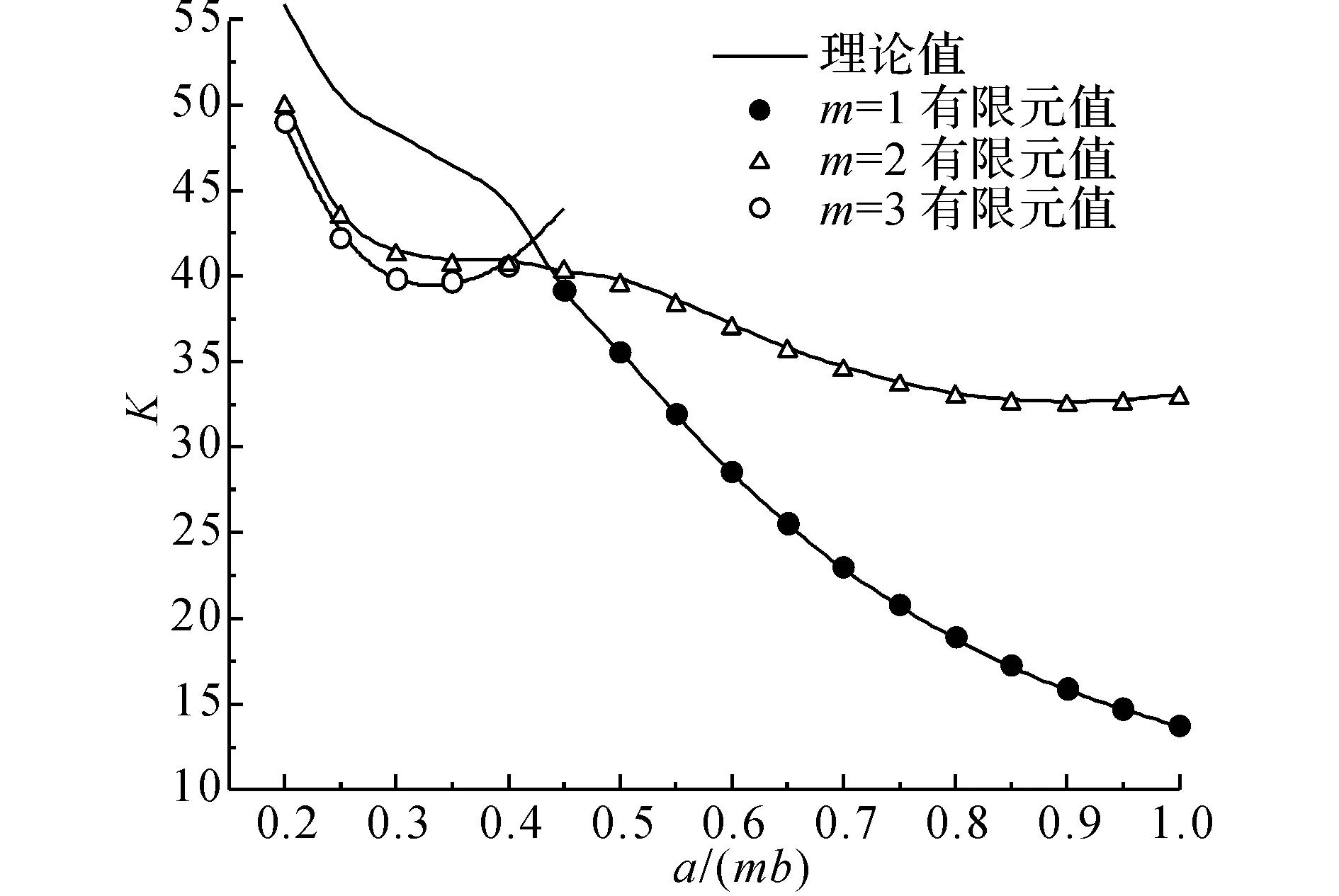
图16 η=1/6 闭口加劲肋结果比对Fig.16 η=1/6 comparison for closed-form Stiffeners

理论结果和ANSYS结果吻合度很好,横向一个半波屈曲时,3种加劲肋的误差都在1%以内,当横向2个半波屈曲时,误差基本在2%以内,最大不超过3%,当横向3个半波屈曲时,采用一定的分配系数δ也能取得很好吻合度,误差在2%以内.

图14中，EIs/(bD)=1.25(1-u2),As/(btp)=0.05,δ=0.4;图15中，EIs/(bD)=1.25(1-u2),As/(btp)=0.045,δ=0.5;图16中，EIs/(bD)=1.5(1-u2),As/(btp)=0.045,δ=0.5.

7 结 论

本文对相对于板几何中心两侧对称布置2根单侧加劲肋板发生屈曲时,单侧加劲肋参与抵抗屈曲的有效抗弯刚度和抗扭刚度进行研究.得到如下结论：

(1)获得了被加劲板参与单侧加劲肋工作的有效宽度的解析表达式,并获得了考虑加劲肋剪切变形的影响的有效抗弯刚度计算公式.

(2)本文的结果表明,布置2根加劲肋时的有效宽度不同于布置一根加劲肋时,而且横向屈曲模态不同时,参与加劲肋工作的板有效宽度也不同.

(3)在加劲板件屈曲问题的求解中,考虑了加劲肋的扭转刚度和翘曲刚度的影响.通过对加劲肋的扭转平衡进行分析,得到了对称布置2根单侧加劲肋的等效扭转常数.

(4)闭口加劲肋有2个腹板连接于母板上,导致母板受力不同于开口加劲肋板,本文对闭口加劲肋采用变形协调等效,从而闭口和开口加劲肋可以采用统一表达式.并通过数值分析结果验证了等效的可行性.

(5)与有限元分析结果的比较表明,本文对3种截面形状的加劲肋得到的有效刚度公式用于求解单侧加劲板的屈曲,均具有很好的精度.可以采用本文公式求解布置2根加劲时的屈曲问题.

[1] JGJ 99-2015.高层民用建筑钢结构技术规程[S].北京.中国建筑工业出版社.2015.

JGJ 99-2015. Technical specification for steel structure of tall building [S]. Beijing. China Architecture&Building Press. 2015.

[2] 童根树,杨章,张磊.钢板剪力墙单侧加劲肋的有效抗弯刚度[J].浙江大学学报：工学版.2015,49(11): 2151-2158.

TONG gen-shu, YANG zhang, ZHANG lei. Effective rigidity of one-side stiffeners in steel shear walls [J].Journal of Zhejiang University: Engineering Science. 2015, 49(11): 2151-2158.

[3] 杨章,童根树,张磊.钢板剪力墙任意布置单侧加劲肋的等效刚度[J].工业建筑.2016, 46(2):125-132.

YANG zhang, TONG gen-shu, ZHANG lei. Equivalent rigidity of one-side stiffeners placed in arbitrary position of steel shear wall [J]. Industrial Construction. 2016, 46(2): 125-132.

[4] 陶文登.钢梁腹板及竖向闭口加劲钢板剪力墙的弹性稳定性[D].杭州：浙江大学2013: 81-100.

TAO wen-deng Elastic stability of girder web planels and steel shear walls vertically strengthened by closed section stiffeners [D]. Hang zhou: Zhejiang University, 2013, 81-100.

[5] 童根树.钢结构的平面内稳定[M]北京：中国建筑工业出版社,2005: 138-141.

[6] 童根树.钢结构的平面外稳定[M](修订版).北京：中国建筑工业出版社,2013:130-131.

[7] TIMOSHENKO S P, GOODIER J N. Theory of Elasticity[M].New York: McGraw-Hill Book Company, 1951: 171-177.

[8] BULSON P S. The Stability of Flat Plates [M]. London: Chatto&Windus Ltd. 1970: 220-221.

[9] SEIDE P. The effect of longitudinal stiffeners located on one side of plate on the compressive buckling stress of the plate-stiffener combination [R]. 2873, Washing-ton: NACA,1953.

[10] OSAMA K. Bedair. A contribution to stability of stiffened plates under uniform compression[J]. Computers & Structures, 1998, 66(5): 535-570.

[11] WANG X, RAMMERSTORFER F.G. Determination of effective breadth and effective width of stiffened plates by finite stripe analyses[J]. Thin-walled strictures, 1996, 26 (4): 261-286.

[12] KATSIKADELIS J T, SAPOUNTZAKIS E. A realistic estimation of the effective breadth of ribbed plates[J]. International Journal of Solids and Structures, 2002, 39(4): 789-799.

[13] STEFANO G, MARCO G, CESARE M R. On the shear lag effective breadth concept for composite hull structures [J]. Ships and Offshore Structures, 2015, 10(3): 272-289.

[14] 聂建国,李法熊,樊建生,等.钢-混凝土组合梁考虑剪力滞效应实用设计方法[J].工程力学,2011, 28(11): 45-51.

Nie Jian-guo, Li Fa-xiong, Fan Jian-shen. Practical design method for steel-concrete composite beam considering shear lag effect[J]. Engineering Mechanics, 2011, 28(11): 45-51.

[15] WADEE M A, FARSI M. Local-global mode interaction in stringer-stiffened plates [J]. Thin-Walled Structures, 2014, 85: 419-430.

Effective Rigidity of two one-side stiffeners arranged symmetrically

YANG Zhang, TONG Gen-shu, ZHANG Lei

(DepartmentofCivilEngineering,ZhejiangUniversity,Hangzhou310058,China)

The buckling of plates with two one-sided stiffeners arranged symmetrically under uniform compression was analyzed to determine the effective stiffness of one-side stiffeners. Second order analyses were conducted for the isolated stiffener and the plate acted by their interactive forces, and they are combined to satisfy the continuity conditions in the longitudinal strains and the deflections on the connecting line. The effect of the free and warping torsion and the shear deformation in the stiffener was included. The critical equations for 3 buckling modes were obtained. Analytic expression of the effective bending and torsion stiffness and the effective breadth were found for each bucking mode. Comparing the plate with only one one-sided stiffener, the effective widths of the plate taking part in the function of the stiffener were different. Comparing with the results of ANASYS analysis, the analytic solution has excellent accuracy regardless of the shapes of the stiffeners.

symmetrical arrangement; buckling modes; two one-side stiffeners; effective rigidity; effective width

2015-10-16.

国家自然科学基金资助项目(51478421).

杨章(1986—)，男，博士生，从事钢板和加劲板稳定性等研究.ORCID: 0000-0002-6952-270X. E-mail：woodchuck228@163.com

童根树，男，教授,博导.ORCID: 0000-0001-5572-2068: E-mail： tonggs@zju.edu.cn

10.3785/j.issn.1008-973X.2016.08.004

TU 391

A

1008-973X(2016)08-1446-10

浙江大学学报(工学版)网址： www.journals.zju.edu.cn/eng