地下增层开挖托换桩的屈曲稳定临界荷载分析

单华峰, 夏唐代, 俞 峰, 胡军华, 潘金龙

(1. 浙江大学 软弱土与环境土工教育部重点实验室,浙江 杭州 310058；2. 浙江大学 滨海与城市岩土工程研究中心,浙江杭州 310058； 3. 浙江理工大学 建筑工程学院,浙江 杭州 310018；4. 岩土科技股份有限公司,浙江 杭州,310001)



地下增层开挖托换桩的屈曲稳定临界荷载分析

单华峰1,2, 夏唐代1,2, 俞 峰3, 胡军华1,2, 潘金龙4

(1. 浙江大学 软弱土与环境土工教育部重点实验室,浙江 杭州 310058；2. 浙江大学 滨海与城市岩土工程研究中心,浙江杭州 310058； 3. 浙江理工大学 建筑工程学院,浙江 杭州 310018；4. 岩土科技股份有限公司,浙江 杭州,310001)

为了研究既有建筑物地下室增层开挖对托换桩基础屈曲稳定的影响,提出托换桩桩身屈曲失稳临界荷载及稳定计算长度的理论计算方法.以甘水巷3号组团地下室建设工程为背景,结合Winkler弹性地基梁理论建立托换桩的桩-土体系总势能方程,利用最小势能原理,导得托换桩屈曲失稳临界荷载及稳定计算长度表达式,并分析托换桩屈曲临界荷载影响因素.结果表明：随着半波数的增加,托换桩的临界荷载逐渐收敛；桩侧摩阻力及桩身自重对托换桩的临界荷载影响不明显；托换桩的临界荷载随开挖深度的增大而急剧减小,随桩身直径的增加而逐渐增大；当开挖深度大于4 m时,土体水平反力比例系数对托换桩临界荷载的影响可忽略不计.

地下室增层；开挖；托换桩；屈曲稳定

2014年底,国务院印发了《关于调整城市规模划分标准的通知》,据此,全国城区常住人口逾500万的特大城市共有16个,逾1 000万的超大城市也有7个.城市的平面化规模发展已带来诸如交通拥堵,建筑拥挤等“城市病”.城市的发展受到土地资源的限制,而向高空发展会增加城市的建筑密度,从而使得城市走向恶性循环,地下空间空开发日渐成为城市合理化发展的优选项.因此,既有建筑物地下室增层开挖技术应运而生,国内外学者对此已进行了一定研究.Iwasaki等[1]介绍了日本名古屋某地下商场新建地铁隧道工程；贾强等[2]通过有限元软件模拟了三层框架结构建筑物地下室增层开挖工况；龚晓南等[3]研究了既有建筑物地下室增层开挖时既有桩侧摩阻力的发挥模式；此后,针对同一工程背景,伍程杰等[4-5]研究了既有桩桩端阻力的发挥模式,在此基础上,还研究了增层开挖施工对既有基桩承载刚度的影响；最近,单华峰等[6]将该方法推广到既有建筑物的群桩基础,研究了增层开挖对既有群桩基础沉降性状的影响.以上学者分析都着眼于分析既有建筑物地下室增层开挖对原有基桩承载力及沉降性状的影响.

早期的研究表明,将普通尺寸桩压入软土中不会发生屈曲失稳,但随着长桩及超长桩的使用,基桩的屈曲问题也将随之而来[7].因此,国内外学者对该问题进行了大量的研究,如Reddy等[8]通过室内试验研究了基桩屈曲失稳现象；Lee等[9]通过能量法提出了基桩屈曲失稳的计算方法；朱大同[10]通过里兹法获得了桥梁桩基稳定计算长度；赵明华[11-12]针对不同基桩的约束状况,提出了不同的屈曲临界荷载计算表示式；邹新军等[13]通过能量法研究了复杂地基反力模式下高承台嵌岩灌注桩的屈曲稳定.

然而,以上学者尚未涉及开挖对基桩稳定性问题的影响.在既有建筑物地下室增开挖工程中,随着开挖深度的增大,桩周土层对托换桩的约束逐渐消失,从而导致了托换桩自由长度增加,在桩顶荷载作用下可能引起托换桩屈曲失稳,因此,有必要研究增层开挖对托换桩屈曲稳定性的影响.故本文以甘水巷3号组团地下室建设工程为背景,结合Winkler弹性地基梁理论建立了托换桩桩-土体系总势能方程,利用最小势能原理,得到托换桩桩身屈曲临界荷载及稳定计算长度的表达式,并分析了半波数,桩身自重,桩侧摩阻力,桩径,开挖深度及土体水平反力系数比例因子对托换桩桩身屈曲临界荷载的影响,以期为相关工程提供参考.

1 工程概况

甘水巷3号组团地下室建设工程位于浙江省杭州市上城区闸口街道甘水巷.建筑场地土层的物理力学性质如表1所示,为典型的软土地区.表中,h为层厚,γs为重度,c为黏聚力,φ为内摩擦角,Es为压缩模量,μ为泊松比,τ为摩阻力特征值.该工程建筑高度为8.01 m,主体为2层框架结构,局部一层,无地下室.由于上部结构荷载不大,故采用柱下独立基础,该基础埋深为1.80 m.由勘察报告可知,场地内地下水属于潜水,随季节降水变化而变化,地下水位约在地表下0.8～1.4 m处.为增加该建筑的使用面积,业主计划开挖一层地下室,预计开挖深度为4.42 m.

2 地下增层开挖施工工艺

不同的上部结构及基础形式会有不同的增层开挖方案[14].本文结合甘水巷3号组团地下室建设工程,简单地介绍该工程的施工流程.本工程采用直径为250 mm及300 mm的钢管桩进行基础托换,如图1所示.首先,开挖至柱下独立基础顶面,并在独立基础四周挖出直径为300 mm及350 mm的孔洞.之后,在相对应的孔洞位置架设小型钻机,泥浆护壁成孔至⑩-2强风化岩层.接着,下放钢管桩至指定标高,同时在钢管桩中倒入细石并采用压力注浆形成细石钢管混凝土桩.通过新浇筑的承台使得钢管混凝土桩与柱连接在一起,使上部结构的荷载通过基桩,而不再是由独立基础传递到土层中,从而实现基础托换,保证了地下室增层开挖的可能性.最后,开挖至拟定标高,并浇筑地下室底板,接长既有建筑结构柱,凿除原基础底板、承台、基础梁及地下室底面上的钢管桩.

表1 土层物理力学性质

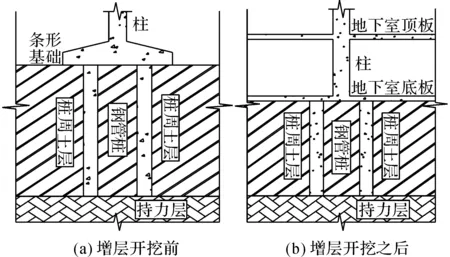
图1 增层开挖前后示意图Fig.1 Sketch of before and after excavation

3 屈曲稳定方程

3.1 屈曲分析

在实际工程中,桩与承台很难做到理想的固结,桩顶约束往往是介于固定支座与铰支座之间,因此,本文假设桩顶约束为弹性嵌固.而在本工程中,钢管桩只是立在稳定的岩层上,尚未嵌岩,因此,本文假设桩端约束为铰支座.本工程岩层强度较高,且上部结构荷载不大,因此,本文假定桩端位移为0.由于群桩基础存在复杂的桩-桩,桩-土相互作用,因此,本文只分析既有建筑物增层开挖对单桩基础屈曲失稳的影响,且本文认为土层开挖方式为层状开挖.其计算模型如图2所示.

桩周土层与桩之间的相互作用则通过一系列Winkler弹簧来模拟,因此,地基反力q(x)可由规范[15]推荐的m法求得

(1)

式中：k为地基反力系数；b0为计算宽度；m为土体水平反力系数的比例系数；y为挠曲函数；x为自变量.

图2 屈曲分析模型Fig.2 Buckling analysis model

由于本工程尚未对托换桩进行水平载荷试验,因此,本文采用以下经验公式来计算m值[16].

(2)

式中：vb为水平位移值,本文取10 mm.

由于本工程所处的场地为多层土,并非均质土层,因此,本文按照陈永辉等[17]建议取土层厚度的加权平均值.

根据现有试验资料[17]可得桩的计算宽度表达式为

b0=kfk0kpd.

(3)

式中：kf为形状换算系数；k0为受力换算系数；kp为各桩间的相互影响系数；d为桩径.

式(3)计算复杂且参数难以确定,因此,钱家欢18-19提出了一种简化的计算方法.

对于圆形桩：

(4)

对于矩形桩：

(5)

式中：b为矩形桩宽度.

结合桩顶、桩端的约束条件,由里兹法可知,桩身屈曲挠曲变形为[11-12]

(6)

式中：ci为待定系数；l为桩长；n为半波数；i为系数,取值范围为1～n.

3.2 桩身屈曲方程建立

桩土体系的总势能Π由桩侧土体的弹性变形能Us、桩身挠曲应变能Up、桩顶荷载势能Vp、桩身自重势能Vg及桩侧摩阻力引起的荷载势能Vf构成,即

Π=Up+Us+Vp+Vf+Vg.

(7)

桩侧土体弹性变形能为

(8)

桩身挠曲应变能为

(9)

式中：E为桩身弹性模量；I为桩截面惯性矩.

本工程于2015年6月23日开始截断托换桩.从截断位置可知,桩顶位置细石混凝土凝结较好,强度较高,需采用风镐将其凿除,如图3(a)所示；而托换桩底部的细石混凝土凝结较差,呈碎散状,如图3(b)所示.其原因可能在于,本工程所处的场地地下水位较高,对细石混凝土的凝固造成了一定的影响.由于细石混凝土的强度比较离散,因此,本文不考虑细石混凝土的强度效应.

图3 现场桩底细石混凝土Fig.3 Fine aggregate concrete at pile tip and pile top in field

由桩顶荷载F产生的势能为

(10)

本文将桩身自重简化为均布线荷载,则桩身自重G产生的势能为

(11)

式中：γ为托换桩重度；A为桩身截面积.

由于桩侧摩阻力的发挥机理复杂且难以确定,为简化计算,本文假定桩侧摩阻力均匀分布.桩侧摩阻力引起的荷载势能为

(12)

式中：U为桩身截面周长.

将式(8)～(12)代入式(7),则桩土体系的总势能方程为

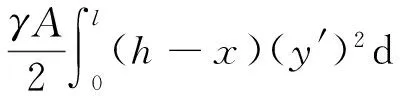
(13)

由最小势能原理[20]可得

(14)

则基桩屈曲稳定方程为D=0,其形式为

(15)

式中：x=Fl2/(π2EI)；aij为行列式D中的元素,该值与桩长,入土深度,桩径及桩侧摩阻力等相关.

以上行列式可通过Jacobian求出其n个特征值,取最小特征值xmin,则桩身屈曲的临界荷载Fcr及稳定计算长度lp分别为

(16)

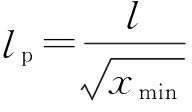
(17)

4 参数分析

限于篇幅的要求,本文只分析半波数,桩身自重,桩侧摩阻力,桩径,开挖深度及土体水平反力系数的比例系数对托换桩屈曲临界荷载的影响.本工程托换桩的极限承载力为900 kN,因此,托换桩的荷载特征值为450 kN,故本文以下分析均假定桩顶荷载为450 kN,且均采用外径为250 mm,壁厚为8 mm的钢管桩进行分析.

4.1 半波数的影响

由于桩侧土体抗力的影响,函数半波数的取值对临界荷载的计算精度极为敏感,如图4所示.由图4可得,在同一开挖深度下,函数半波数n从2增加到3,相应的临界荷载呈急剧下降；之后,随着半波数的增大,临界荷载缓慢收敛.当半波数n=15时,不同开挖深度下的临界荷载已收敛,与赵明华等[11-12]提出的当半波数n≥16时,基桩临界荷载收敛的结论基本一致.因此,本文以下分析采用的半波数均为15.

图4 不同开挖深度下半波数对临界荷载的影响Fig.4 Effect by critical load with half-wave number under different excavation depth

4.2 侧摩阻力及桩身自重的影响

在竖向荷载用下,桩侧摩阻力是一个关键的参数.本节分析在同一开挖深度下,桩侧摩阻力及桩身自重对桩身屈曲临界荷载的影响,如表2所示.表中αw、αs及αws分别为在同一开挖深度处,不考虑桩身自重,不考虑桩侧摩阻力、桩身自重及桩侧摩阻力均不考虑时的基桩屈曲临界荷载与同时考虑桩身自重及桩侧摩阻力的比值,l0为开挖深度.由表2可知,在同一开挖深度下,αw、αs及αws值均接近于1.0,因此,是否考虑侧摩阻力及桩身自重对桩身屈曲稳定临界荷载影响微乎其微,与文献[11,21]报道一致.

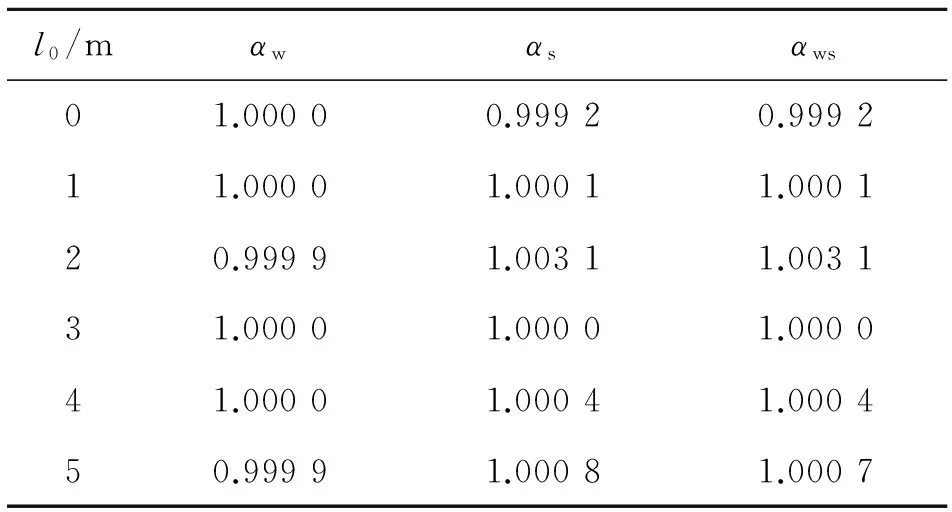
表2 侧摩阻力与自重对临界荷载的影响

4.3 开挖深度的影响

在既有建筑物地下增层开挖工程中,随着开挖深度的增加,托换桩的荷载传递机理也将随之发生变化,如图5所示.因此,在增层开挖工程中,开挖深度是一个需要控制的量.图中αl0为开挖深度l0时的基桩临界荷载与尚未开挖时的基桩临界荷载之比.由图5可知,随着开挖深度的增加,托换桩的临界荷载比急剧减小,当开挖深度为5 m时,该比值降低到0.03,临界荷载降低了33.3倍,其原因可能是随着开挖深度的增加,桩侧土层对托换桩的约束逐渐减少,托换桩的自由长度增加,从而导致托换桩发生屈曲失稳.

图5 开挖深度对临界荷载的影响Fig.5 Effect by critical load with different excavationdepth

图6 不同开挖深度下桩径对临界荷载的影响Fig.6 Effect by critical load with pile diameter under different excavation depth

4.4 桩径的影响

本工程采用直径为250 mm及300 mm的钢管桩进行基础托换,因此,本小节将分析托换桩桩身直径对屈曲临界荷载的影响,如图6所示.图中αd为在同一开挖深度下,桩径为d的基桩临界荷载与桩径为250 mm的基桩临界荷载之比.由图6可知,在同一开挖深度下,随着桩径的增大,不同桩径的临界荷载之比αd也逐渐增加,如在开挖深度为1 m时,桩径为300 mm时的临界荷载比为1.94.桩径从250 mm增加到300 mm时,相应的桩顶临界荷载增加了94%,其原因可能是,随着桩径的增加,桩身的挠曲应变能及桩侧土体弹性变形能都相应的增加,从而使得基桩的临界荷载也在逐步增大.

4.5 m值的影响

图7 不同开挖深度下m值对临界荷载的影响Fig.7 Effect by critical load with different value of m under different excavation depth

在地下增层开挖托换桩的屈曲稳定临界荷载计算过程中,m值是一个非常重要的量.因此,本节通过改变m值的取值范围来研究其对地下增层开挖托换桩临界荷载的影响,如图7所示.由图7可知,在同一开挖深度下,随着m值的增大,临界荷载逐渐增加,在开挖深度为0.2 m,从0.6m增加到1.4m时,相应的临界荷载增大了1.38倍；随着开挖深度的增加,不同m值对临界荷载的影响逐渐减小,当开挖深度大于4 m时,不同的m值对托换桩临界荷载的影响微乎其微,图中曲线基本重合,其对托换桩临界荷载的影响可忽略不计.

5 结 论

本文结合甘水巷3号组团地下室建设工程,通过理论分析,研究了既有建筑物地下增层开挖对托换桩屈曲稳定的影响.得出了以下结论：

(1)结合Winkler弹性地基梁理论建立了桩土体系总势能方程,通过最小势能原理,得到了既有建筑地下室增层开挖工程中托换桩的屈曲稳定临界荷载及计算长度的表达式.

(2)分析了既有建筑物地下室增层开挖工况下托换桩屈曲临界荷载的影响因素,获知：随着半波数n的增加,托换桩的临界荷载逐渐收敛,本文取半波数n=15；桩侧摩阻力及桩身自重对托换桩的临界荷载影响不大,可忽略不计；托换桩的临界荷载将随开挖深度的增大而急剧减小,随桩身直径的增加而逐渐增大；随着m值的增大,托换桩的临界荷载逐渐增大,当开挖深度大于4 m时,m值对托换桩临界荷载的影响可忽略不计.

[1] IWASAKI Y, WATANABE H, FUKUDA M, et al. Construction control for underpinning piles and their behavior during excavation [J]. Geotechnique,1994, 44(4): 681-689

[2] 贾强,张鑫,应惠清.桩基础托换开发地下空间不均匀沉降的数值分析[J].岩土力学,2009,30(7)： 2053-2057.

JIA Qiang, ZHANG Xin, YING Hui-qing. Numerical analysis of settlement difference for pile foundation underpinning for constructing underground space [J]. Rock and Soil Mechanics, 2009, 30(7): 2053-2057.

[3] 龚晓南,伍程杰,俞峰,等.既有地下室增层开挖引起的桩基侧摩阻力损失分析[J].岩土工程学报,2013,35(11): 1957-1964.

GONG Xiao-nan, WU Cheng-jie, YU Feng， et al. Shaft resistance loss of piles due to excavation beneath existing basements [J]. Chinese Journal of Geotechnical Engineering, 2013, 35(11): 1957-1964.

[4] 伍程杰,龚晓南,俞峰,等.既有高层建筑地下增层开挖桩端阻力损失[J].浙江大学学报：工学版,2014,48(4): 671-678.

WU Cheng-jie, GONG Xiao-nan, YU Feng， et al. Pile base resistance loss for excavation beneath existing high-rise building [J]. Journal of Zhejiang University ：Engineering Science, 2014, 48(4): 671-678.

[5] 伍程杰,龚晓南,房凯,等.增层开挖对既有建筑物桩基承载刚度影响分析[J].岩石力学与工程学报,2014,33(8): 1526-1535.

WU Cheng-jie, GONG Xiao-nan, FANG Kai, et al. Effect of excavation beneath existing building on loading stiffness of piles [J]. Chinese Journal of Rock Mechanics and Engineering,2014,33(8): 1526-1535.

[6] 单华峰,夏唐代,俞峰,等.既有建筑物地下室增层开挖群桩沉降性状研究[J].岩土工程学报,2015,37(增刊1)： 46-50.

SHAN Hua-feng, XIA Tang-dai, YU Feng， et al. Settlement of pile groups associated with excavation beneath existing basement [J]. Chinese Journal of Geotechnical Engineering, 2015, 37(Supp1): 46-50.

[7] POLOUS H G, DAVID E H. Pile foundation analysis and design[M]. New York: John Wiley & Sons Inc, 1980: 323-324.

[8] REDDY A S, VALSANGKAR A J. Buckling o fully and partially embedded piles [J]. Journal of Soil and Mechanics and Foundation Division, ASCE, 1970,96(6): 1951-1965.

[9] LEE K L. Buckling of partially embedded piles in sand [J]. Journal of Soil and Mechanics and Foundation Division, ASCE, 1968,94(1): 255-270.

[10] 朱大同.端部嵌固桩的计算长度[J].铁路标准设计通讯,1974(5): 27-29.

ZHU Da-tong. Calculation length of piles fixed in both sides [J]. News Report in Railway Standard Design,1974, (5): 27-29.

[11] 赵明华.桥梁基桩稳定计算长度[J].工程力学,1987,4(1): 94-105.

ZHAO Ming-hua. Buckling equivalent length of piles [J]. Engineering Mechanics, 1987,4(1): 94-105.

[12] 赵明华.桥梁桩基的屈曲分析及试验[J].中国公路学报,1990,3(4): 47-57.

ZHAO Ming-hua. Buckling analysis and tests of bridge piles [J]. China Journal of Highway and Transport, 1990,3 (4): 47-57.[13] 邹新军,赵明华,刘光栋.复杂地基反力模式下高承台嵌岩灌注桩的屈曲稳定分析[J].岩土力学,2008,29(4)： 963-967.

ZOU Xin-jun, ZHAO Ming-hua, LIU Guang-dong. Buckling analysis of cast-in-situ rock-socketed piles with highrise pile cap under complicated subgrade reaction modulus [J]. Rock and Mechanics, 2008,29(4)： 963-967.

[14] 黄兴棣.建筑物鉴定加固与增层改造[M].北京：中国建筑工业出版社,2008: 38-39.

[15] JTGD63-2007.公路桥涵地基与基础设计规范[S].北京：人民交通出版社,2007.

JTGD63-2007. Code for design of ground base and foundation of highway bridge and culverts [S]. Beijing: China Communications Press, 2007.

[16] JGJ120-2012.建筑基坑支护技术规程[S].北京：中国建筑工业出版社,2012.

JGJ120-2012. Technical specification for retaining and protection of building foundation excavations [S]. Beijing: China Architecture & Building Press, 2012.

[17] 陈永辉,王新泉,刘汉龙.基于尖点突变理论的Y型桩屈曲临界荷载分析[J].工程力学,2009,26(4)： 119-127.

CHEN Yong-hui, WANG Xin-quan, LIU Han-long. Buckling critical load analysis of y style vibro-pile based on cusp catastrophe theory [J]. Engineering Mechanics, 2009,26(4)： 119-127.

[18] 钱家欢.土力学[M].南京:河海大学出版社,1995:226-227.

[19] JGJ 94-2008.建筑桩基技术规范 [S].北京：中国建筑工业出版社,2008.

JGJ 94-2008.Technical code for building pile foundations [S]. Beijing: China Architecture & Building Press, 2008.

[20] S.P.铁摩辛柯,J.N.古地尔.弹性理论[M].北京：高等教育出版社,2013: 235-236.

[21] 赵明华, 王季柏. 基桩计入摩阻力的屈曲分析[J].岩土工程学报,1996,18(3)：87-90.

ZHAO Ming-hua, WANG Ji-bai. Buckling analysis of piles with side resistance considered [J]. Chinese Journal of Geotechnical Engineering, 1996,18(3): 87-90.

Buckling stability analysis on critical load of underpinning pile for excavation beneath existing building

SHAN Hua-feng1,2, XIA Tang-dai1,2, YU Feng3, HU Jun-hua1,2PAN Jin-long4

(1.MOEKeyLaboratoryofSoftSoilsandGeoenvironmentalEngineering,ZhejiangUniversity,Hangzhou310058,China;2.ResearchCenterofCostalandUrbanGeotechnicalEngineering,ZhejiangUniversity,Hangzhou310058,China;3.SchoolofCivilEngineeringandArchitecture,ZhejiangSci-TechUniversity,Hangzhou310018,China;4.TheGeotechnicalTechnologiesHoldingsCo.Ltd.,HangzhouZhejiang310001)

A theoretical analysis was carried out to estimate the critical bucking capacity and the effective length of the underpinning pile. The influence of excavation beneath existing building on the buckling stability of underpinning pile was studied by the No. 3 subsection of the Ganshuixiang construction project. The total potential energy of the pile-soil system was determined by employing the Winkler’s elastic beam theory. The expressions of critical buckling capacity and effective length of underpinning pile were deduced by using the minimum potential energy principle. The influence factors on the critical buckling capacity of underpinning pile were analyzed. Results indicate that, the critical buckling capacity of underpinning pile converges with the half-wave number increasing; the shaft resistance and the self-weight of pile impose little effect on the buckling load of pile shaft; the critical buckling capacity decreases rapidly with excavation depth increasing but increases steadily with pile diameter increasing.Furthermore, the proportional coefficient of horizontal reaction force imposes insignificant effect on the buckling load when the excavation depth exceeds 4 m.

floor-addition of basement; excavation; underpinning pile; buckling stability

2015-11-27.

国家自然科学基金资助项目(41472284，51378463).

单华峰(1987— )，男，博士生，从事桩基工程等研究.ORCID：0000-0001-5184-0999. E-mail：shanhf@zju.edu.cn

俞峰，男，教授.ORCID：0000-0003-0634-355X. E-mail：pokfulam@163.com

10.3785/j.issn.1008-973X.2016.08.001

TU 473

A

1008-973X(2016)08-1425-06

浙江大学学报(工学版)网址： www.journals.zju.edu.cn/eng