基于遗传算法的动车运用所一级检修作业计划优化

童佳楠，聂 磊，贺振欢

（北京交通大学 交通运输学院，北京 100044）

基于遗传算法的动车运用所一级检修作业计划优化

童佳楠，聂 磊，贺振欢

（北京交通大学 交通运输学院，北京 100044）

在动车运用所的洗车线、检修线等固定设备已定的前提下，合理安排动车组一级检修作业计划对提高动车运用所的检修能力具有重要意义。动车组由于长短编组不同，在检修时对双列位检修线的占用情况也不同。以同一列位在同一时间最多只能被1列动车组占用的时空相容性及动车组运用计划为约束条件，以最后 1 列动车组检修完成时间最小为目标，建立动车所一级检修作业计划优化模型，将问题转化为带特殊工艺约束的混合 flow-shop 调度问题，并采用自适应的遗传算法进行求解。最后以某动车运用所为例，验证模型和算法的可行性及有效性。

动车运用所；一级检修；混合 flow-shop；遗传算法

1概述

动车运用所 (以下简称“动车所”) 检修能力是动车组交路勾画和运行图编制的重要约束条件，其中一级检修以检为主，是动车组最日常的维修，一般安排在夜间进行。目前各个动车所由于检修资源有限，每晚的检修任务相当繁重，因而合理安排动车组一级检修作业计划、提高动车组检修效率具有十分重要的意义。不考虑具体检修内容，动车组一级检修计划本质上是动车组在各个股道之间的调车作业计划。

许多专家和学者对相关问题进行了研究。王忠凯等[1]对动车所各级检修的调车作业计划进行研究，以股道连通关系、时空占用相容性、动车组运用计划和检修计划为约束，以减少动车运用所关键检修线区无效占用时间和减少调车路径费用为目标，将问题转化为具有附加时空约束的车间调度问题，并采用改进的最大最小蚁群系统进行求解。张惟皎等[2]对动车所存车线的运用进行研究，以给定动车组占用存车线时间为前提，以同一列位在同一时间最多只能被 1 列动车组占用的相容性条件为约束，以提高存车线利用率和减少调车作业走行距离为优化目标，建立动车所存车线运用的 0-1 规划优化模型，并设计 k 剔除邻域的模拟退火算法进行求解。崔炳谋等[3]分析编组站作业进路选排问题的本质，以各任务的延误时间加权总和最小为目标，以任务的前后工序选择路径为动态约束建立模型，并采用遗传算法求解。刘常青等[4]将动车组一级检修问题转化成 flow-shop 问题并运用遗传算法对问题进行求解。Reeves C R[5]、Ishibuchi H 等[6]、王万良等[7]应用遗传算法求解 flow-shop 调度问题，而混合 flow-shop 调度问题 (Hybrid Flow-Shop Scheduling Problem，HFSP) 是一般 flow-shop 调度问题的推广，由于在某些工序上存在并行机制而更为复杂，而且精确算法难以处理大规模复杂问题，因而启发式算法被广泛用于实际生产环境中 HFSP 问题的求解。

综上所述，目前的研究中将动车所一级检修作业计划问题转化为 flow-shop 问题进行研究的较少，并且没有考虑检修线的双列位情况。我国动车所检修线一般采用双列位设计，实际调度作业更加复杂。结合检修线双列位的特点，尝试将一级检修作业计划问题看成是带有特殊工艺约束的混合 flow-shop 调度问题，建立优化模型，并运用自适应的遗传算法进行求解。

2问题描述

典型动车所的布局如图1所示，包括存车场、洗车线、检修库和牵出线等线区，每个线区包括若干条股道，不同线区承担不同的检修作业任务。

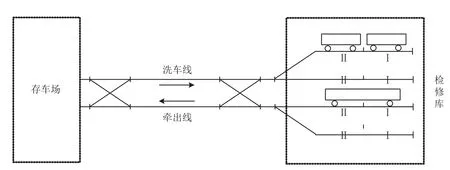
图1　典型动车运用所布局示意图

我国动车所检修线区的股道一般分为 2 个列位，在进行检修时，1 列短编组 (8 节编组) 动车组占用 1 个列位，1 列长编组 (16 节编组) 动车组同时占用同一条检修线的 2 个列位。每个列位有单独的供电系统，检修时互不影响，因而每条检修线 1 次可检修 1 列长编组动车组或同时检修 2 列短编组动车组。由于调车作业进路的安排，短编组动车组进出其占用的列位时，可能会经过其所占用列位的相邻列位，因而当 2 列短编组动车组同时占用同一条检修线时，必须考虑它们进出检修线的方向和占用列位的时间是否冲突，以保证同一列位同一时间最多只能被 1 列动车组占用，称之为列位占用相容性。

对于混合 flow-shop 调度问题，可以把各线区的股道看成机器，待检动车组看成待加工的工件。在一般的混合 flow-shop 调度问题中，机器与工件之间是一对一的匹配关系，1 台机器 1 次可加工且只能加工 1 个工件。而当列车与检修线之间处于多对一的动态匹配关系时调度问题更加复杂，因而可以将问题看成一种带有特殊工艺约束的混合 flowshop 调度问题。

3动车所一级检修作业计划优化模型

定义动车所的所有线区集合为 D，线区序号 d = 1，2，…，ND，其中 d ∈ D，d = 1 表示洗车线区，d = 2 表示检修线区，d = 3 表示牵出线区；线区 d 的股道集合为 LD，股道序号为 l = 1，2，…，ND，l ∈ Ld；某些特殊线区 (如检修线区) 的每条股道是双列位，设列位集合为 Vdl，序号为 v = 1，2，v ∈ Vld；动车组集合为 E，序号为 e = 1，2，…，NE，e ∈ E，E = EL∪ ES，其中 EL为长编组列车集合，ES为短编组列车集合；列车 e 进入动车所的时间和驶出动车所的时间分别设为，，则列车 e在动车所内总停留时间；ted表示列车 e 在线区 d 规定的最小作业时间，表示列车 e 进入线区 d 的股道 l 的时间，表示列车 e 离开线区 d 的股道 l 的时间，则有；列车在咽喉区 (包括存车线与洗车线之间和检修线与洗车线之间) 的走行时间为 tt。

定义下列决策变量：xedl为 0-1 变量，表示列车 e 对线区 d 的股道 l 的占用情况，当列车 e 占用 l 进行作业时为 1，否则为 0；对于特殊线区 (如检修线区)，定义 0-1 变量xedlv，表示列车 e 对股道 l 的列位 v 的占用情况，当列车 e 占用股道 l 的列位 v 时为 1，否则为 0；yecdl为 0-1 变量，表示线区 d 的股道 l 被动车组 e 和 c 的占用顺序，当 e 先于动车组 c 占用股道 l 时为 1，否则为 0；zecdl为 0-1 变量，如果动车组 e，c 均为短编组，e 和 c 相邻且 e 先于 c 占用股道 l 时为 1，否则为 0。

以最后 1 列动车组检修完成时间最小，即最后1 列车驶出牵出线区 (d = 3) 时间最小为目标函数，建立优化模型如下。

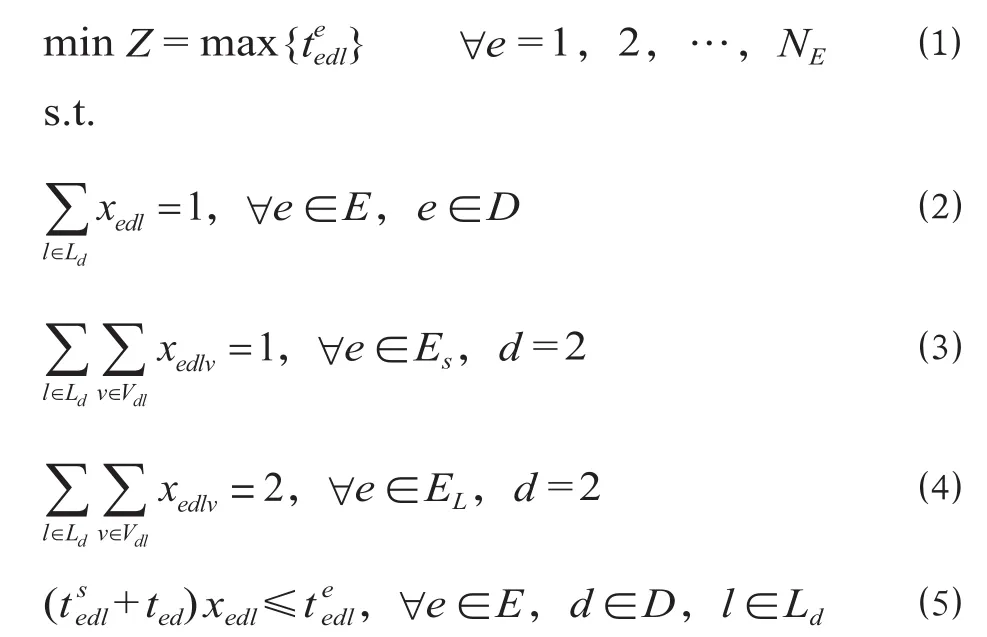
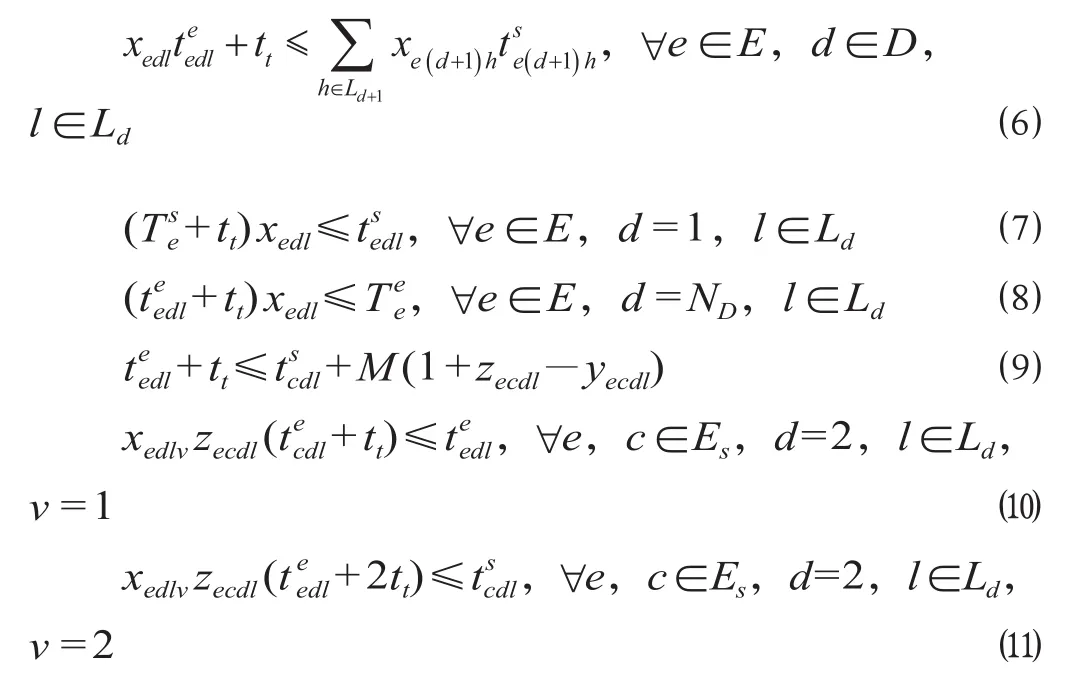
⑵ 式表示动车组在每个线区必须选择且只能选择 1 条股道进行作业；⑶ 式表示如果动车组为短编组，则其在检修线区必须选择且只能选择 1 个列位进行作业；⑷ 式表示如果动车组为长编组，则其在检修线区必须选择且只能选择 2 个列位进行作业；⑸ 式表示动车组必须在相应线区停留足够时间，满足检修计划中的作业持续时间要求；⑹ 式表示上 1 个线区作业结束后才能进入下 1 个线区；⑺ 式和 ⑻ 式为动车组运用计划约束，其中 ⑺ 式表示动车组必须在进所后才能进行检修；⑻ 式表示动车组必须在运用计划规定的离所时间之前修完；⑼ 式、⑽ 式和 ⑾ 式为股道或列位时空占用相容性约束，其中 ⑼ 式表示当前动车组必须等上 1 列完全离开股道后才能进入该股道，M 为一足够大的数；⑽ 式表示在检修线区，对于同时在同一条股道上的 2 列短编组动车组，如果前车选择列位 1，则前车必须等后车检修完才能驶出股道；⑾ 式表示在检修线区，对于某条股道的相邻的 2 列短编组动车组，如果前车选择列位 2，说明该股道此时正同时被 2 列短编组动车组占用，后车必须等当前检修线上的 2 列车都驶出后才能进入检修线。

4遗传算法设计

动车所一级检修作业计划优化问题属于 NP-hard问题，随着待检动车组、动车运用股道以及作业工序的增加，会产生组合爆炸，因而难以用传统的数学规划方法进行求解。采用自适应遗传算法来求解该问题，首先对基因编码、计算目标值，在此基础上设计适应度函数，通过个体选择和个体交叉来实现自动优化，并通过基因变异来修复和补充在选择和交叉过程中可能丢失的某些遗传基因；同时，针对检修线区双列位的特殊性，增加相应的业务规则，使得算法更加有效。

4.1基因编码

假设动车组一级检修需要经过 S 个线区，待检动车组数量为 N，首先构造一个 S×N 维的编码矩阵为

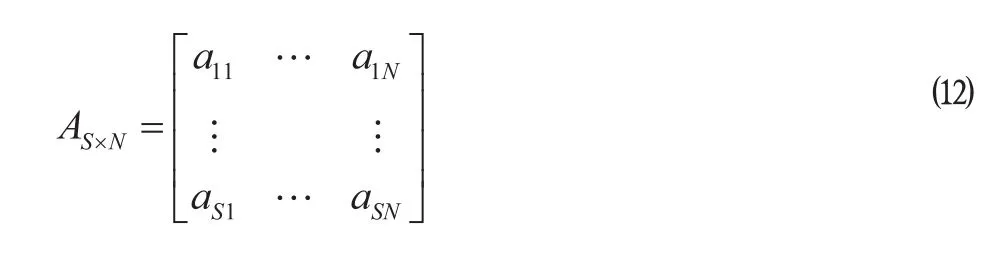
编码矩阵中的元素 aij是区间 (1，Mi+ 1) 上随机产生的实数，Mi表示线区 i 的股道数量，表示动车组j 在第 i 个线区的第 int (aij) 条股道上进行相应的作业，其中 int (aij) 是对实数 aij的取整。显然，很有可能会出现 int (aij) =int (aik) ，j≠k，表明多个动车组被分配到同一线区的同一条股道上进行作业。这时，如果是在洗车线区，则按照 a1j的升序来安排动车组的顺序；否则，根据每个动车组在前一个线区的完成时间来确定其顺序，前一个线区的作业先完成的先进行；如果时间相同，则也按照 aij的升序来安排。

4.2目标值计算

由于检修线区双列位的特殊性，为减少股道的空闲时间，在根据基因编码计算动车组在各线区股道开始和结束作业的具体时刻时，应遵循以下规则。

（1）优先满足关键线区的调度安排，针对检修线区作业时间长且双列位使调度更加复杂的情况，应优先满足检修线区的时间。

（2）尽量将短编组动车组安排在列位 1 上进行检修，以保证列位 2 对其他短编组动车组仍可用。

（3）当前动车组为短编组时，如果此时列位 2可用且列位 1 上的动车组检修作业尚未过半，则安排动车组在列位 2 上检修，否则应待列位 1 上的动车组检修完了再安排其在列位 1 上检修。

根据基因编码可以确定每列动车组在各个线区的排列情况。设 c 为 d 的紧前线区，当前动车组被安排在线区 d 的股道 l 上，tdl为股道 l 的空闲时刻，tdlv为股道 l 的列位 v 的空闲时刻，为动车组 i 进所时间，为动车组 i 在线区 d 的开始和结束作业的时间，td为线区 d 要求的最小作业时间，tt为动车组在各线区之间调车走行时间，n 为待检动车组数量。

具体计算动车组在各线区股道开始和结束作业时间的步骤如下。

第 1 步：初始化 i = 0，tdl= 0 (d = 1，2，3 )。

第 3 步：计算在检修线区 (d = 2) 的时间，如果动车组 i 为短编组，转第 4 步；如果 i 为长编组，转第 7 步。

第 4 步：如果列位 1 被占用、列位 2 空闲且此时列位 1 上的动车组检修作业尚未过半，则安排 i到列位 2 上，转第 5 步；否则安排 i 到列位 1 上，转第 6 步。

第 9 步：如果i≤n，则i= i+1，转第 2 步；否则，计算结束。

4.3适应度函数设计

以目标函数值的倒数作为适应度函数，即

根据 ⑻ 式的动车组运用计划约束，要求每列车检修完成时间应该早于其规定的出所时间，以保证第 2 天交路计划的正常运行；否则，原则上该染色体表示的是无效解，应令其适应度值f = 0，在进行选择操作时可以直接淘汰掉。但是，当动车运用所的股道较少，检修资源不足时，如果在较短的时间内为动车运用所安排过多的一级检修作业，可能无法满足全部动车组的检修作业约束，模型没有可行解。此时，应将约束条件 ⑻ 进行松弛，即可以不保证全部动车组的检修计划约束，满足尽量多的动车组出所时间。

具体操作是当动车组 e 的检修完成时间超过交路计划规定的检修截止时间时，增加适应度函数惩罚值，对其进行修正，即

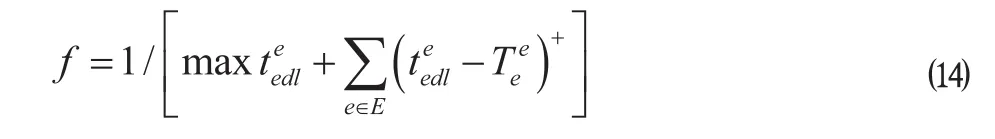
4.4个体选择

选择操作通过比较个体的适应度值来判断个体优良程度，采用轮盘赌注方法，每个个体被选择的概率与其适应度值的大小成比例。个体被选择概率为

4.5个体交叉

运用自适应遗传算法，交叉概率 Pc能够随着适应度自动改变。当种群各个体适应度趋于一致或趋于局部最优时，使 Pc增加，从而跳出局部最优；而当群体适应度比较分散时，使 Pc减小，以利于优良个体的生存。Pc按照 ⒃ 式进行调整。

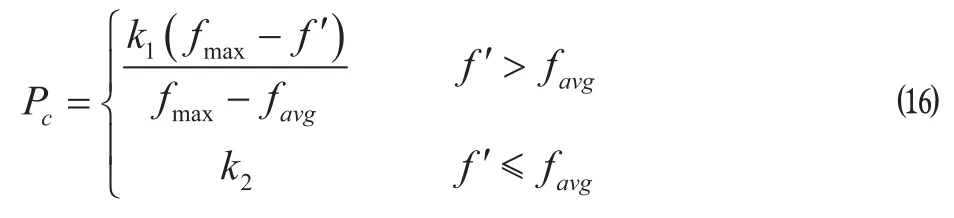
式中：fmax是种群中最大的适应度值；favg是每代种群的平均适应度值；f ' 是要交叉的 2 个个体中较大的适应度值；k1、k2是 (0，1) 之间的常数。

4.6基因变异

变异的目的是保持群体的多样性，修复和补充在选择和交叉过程中可能丢失的某些遗传基因。变异步骤如下。

（2）如果 d ＜ Pm，则+ aij；否则，a'ij= (aij－1)×rand (1) + 1。其中，d 为实数，aij为进行变异的个体，a'ij为变异后的个体。通过这种变异方法可保证a'ij在 (1，Mi+ 1) 区间内，也就可以保证个体的合法性，同时变异操作也具有很好的随机性。

5案例分析

以某动车所某日实际检修的动车组为算例，验证模型和算法的可行性。该动车所的检修设备布局情况如图1 所示，共有 1 条洗车线、3 条检修线和 1条牵出线。动车组进行一级检修时，其中洗车耗时30 m in，检修耗时 3 h，由牵出线调出需要 10 m in，各咽喉区调车走行时间为 5 m in。该动车所待检修列车运用计划如表1所示。

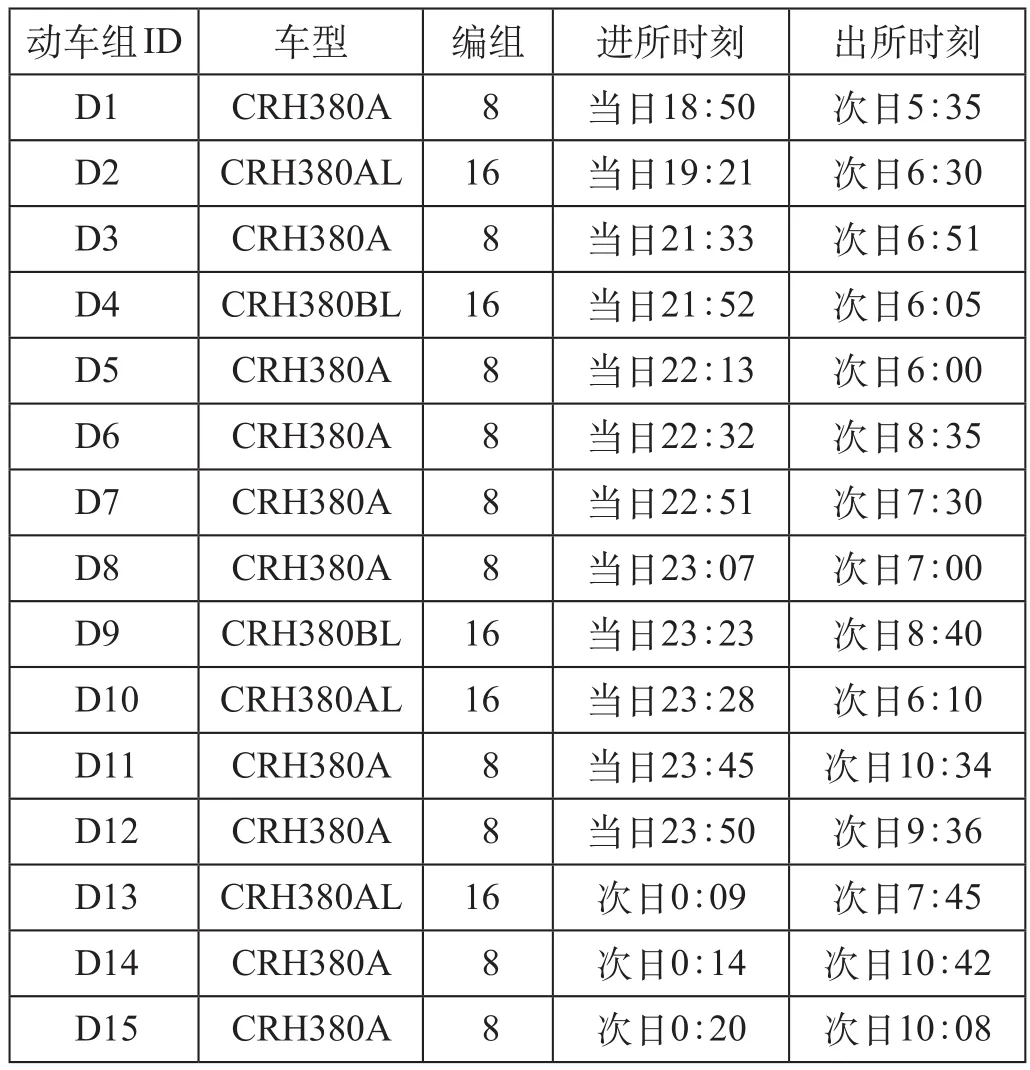
表1　某动车所待检动车组进出所时间计划

经过多次实验比较，遗传算法采用以下参数设置，求解效率和效果最佳：最大迭代次数 M = 500，种群规模 P = 30，交叉概率 Pc= 0.8，变异概率 Pm= 0.1，交叉概率调整系数 k1= 0.5，k2= 0.5。最终求解得出的该所一级检修作业最迟完工时间为次日11 ∶ 13，即最后 1 列动车组 D 14 检修完成由牵出线驶入存车线的时刻为次日 11 ∶ 13。动车组在各个线区股道作业起止时间如表2所示，对应的甘特图如图2 所示。

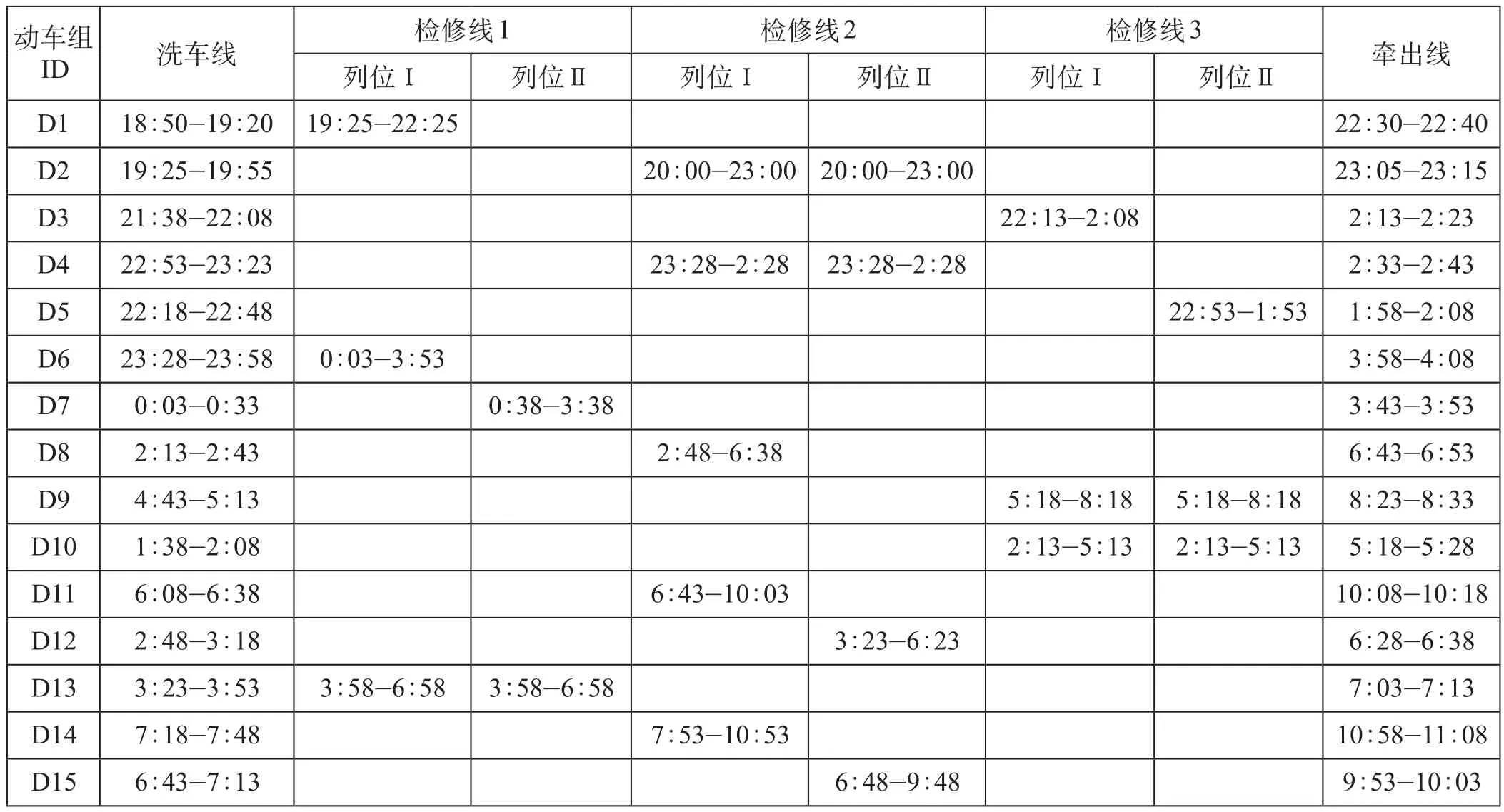
表2　动车组在各个线区股道作业起止时间

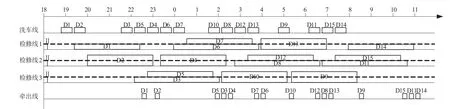
图2　股道占用甘特图

由求解结果可以看出，该动车所最繁忙的时刻在 23 ∶ 00至次日 8 ∶ 00，最后 1 列车 D 14 检修完成时间超过其交路计划规定的出所时间，说明该所当日的检修作业十分紧张，可以考虑增加洗车线和检修线来缓解繁忙的检修任务。

6结束语

目前我国铁路各个动车所由于检修资源有限，每晚的检修任务相当繁重，需要合理安排动车组一级检修作业计划。动车所一级检修作业计划优化问题属于 NP-hard 问题，用传统的数学规划方法求解困难，因而将该问题转化为带特殊工艺约束的混合flow-shop 调度问题，并采用自适应的遗传算法求解。算例验证结果表明，与目前动车所的人工调度方式相比，动车所一级检修作业计划优化模型能够合理利用检修线双列位的特点，有效利用检修资源，提高检修线利用率及动车组的检修效率，从而提高动车所的检修吞吐能力，减轻调度人员的工作量。

[1] 王忠凯，史天运，张惟皎，等. 动车运用所调车作业计划优化编制模型与算法[J]. 铁道学报，2013，35(8)：1-9.

WANG Zhong-kai，SHI Tian-yun，ZHANG Wei-jiao，et al. Model and A lgorithm for Optim ized Formulation of Scheduled Shunting Operation Plans of Electric Multiple UnitsDepots[J]. Journal of the China Railway Society，2013，35(8)：1-9.

[2] 张惟皎，史天运，陈 彦. 动车运用所存车线运用方案优化模型与算法[J]. 中国铁道科学，2013，34(1)：121-125.

ZHANG Wei-jiao，SHI Tian-yun，CHEN Yan. Model and Algorithm for Optimized Formulation of Operation Plans of Storage Tracks[J]. China Railway Science，2013，34(1)：121-25.

[3] 崔炳谋，马钧培，张 朴. 编组站进路调度优化算法[J].中国铁道科学，2007，28(2)：100-105.

CUI Bing-mou，MA Jun-pei，ZHANG Pu. An Optim ization Algorithm for Route Dispatching in Marshalling Station[J]. China Railway Science，2007，28(2)：100-105.

[4] 刘常青，吴志强，李 强，等. 北京动车检修基地能力分析与对策[J]. 铁道运输与经济，2012，34(7)：88-90.

LIU Chang-qing，WU Zhi-qiang，LI Qiang，et al. Analysis and Countermeasures on the Capacity of Beijing EMU Depot[J]. Railway Transport and Economy，2012，34(7)：88-90.

[5] Reeves C R. A Genetic A lgorithm for Flow Shop Sequencing[J]. Computers and Operations Research，1995，22(1)： 5-13.

[6] Ishibuchi H，Yam amoto N，M urata T，et al. Genetic A lgorithms and Neighborhood Search A lgorithms for Fuzzy Flow-Shop Scheduling Problems[J]. Fuzzy Sets and Systems，1994，67(1)：81-100.

[7] 王万良，姚明海，吴云高，等. 基于遗传算法的混合 Flow-Shop 调度方法[J]. 系统仿真学报，2002，14(7)：863-867.

WANG Wan-liang，YAO M ing-hai，WU Yun-gao，et al. Hybrid Flow-Shop Scheduling Approach based on Genetic A lgorithm[J]. Journal of System Simulation，2002，14(7)：863-867.

[8] Dorndorf U，Pesch E. Evolution Based Learning in a Job-Shop Scheduling Environment[J]. Computers and Operations Research，1995，22(1)：25-40.

责任编辑：吕向茹

暑运过半铁路旅客发送量持续高位运行

2016年 7 月 1 日暑运启动以来，中国铁路总公司始终坚持以实现旅客 “安全出行、方便出行、温馨出行”常态化为目标，克服不良天气频发的影响，优化运力安排，加强售票组织，提高服务质量，实现了暑运安全平稳、秩序良好。7 月份，全国铁路旅客发送量累计达到 26 877.7 万人次，同比增长 8.5%。

2016年以来，铁路部门深入推进供给侧结构性改革，全国铁路于 5 月 15 日实施了新的列车运行图，铁路客运服务供给的品质和效率得到进一步提升，旅客出行更加方便快捷。暑运期间，铁路部门统筹安排运输能力，做好旅客运输服务保障工作，最大限度地满足广大旅客出行需求。除日常开行的旅客列车外，铁路部门还安排增开跨铁路局中长途旅客列车 44.5 对，高铁、客运专线实行高峰运行图。

暑运期间，学生流、旅游流、探亲流、商务流交织，铁路旅客发送量始终保持高位运行。7 月 16 日，全国铁路发送旅客 963.1 万人次，创历年暑运单日旅客发送量历史新纪录。7 月份，全路动车组列车旅客发送量突破 1 亿人次大关，达到13 814.3 万人次，占铁路旅客发送总量的 51.4%，同比增长 26.9%。

7 月份，大范围、长时间暴雨等极端天气频发。铁路部门全力做好抗击水害、抗洪防汛工作，重点抓好受水害影响区段设备的抢修整治，全面消除隐患。水害发生时，铁路部门积极做好应急处置，及时恢复运行秩序，强化汛期旅客服务，为旅客出行创造了良好环境。

（摘自《人民铁道》报）

Optimization of First-Level Maintenance Plan in EMU Depot based on Genetic Algorithm

TONG Jia-nan，NIE Lei，HE Zhen-huan

(School of Traffic and Transportation, Beijing Jiaotong University, Beijing 100044, China)

Under the precond itions of fixed equipm ents like washing siding and main tenance tracks in EMU depo t having been determined, reasonable a rrangement of first-leve l EMU maintenance plan has an im portant significance for increasing the depot’s maintenance capacity. As each maintenance track canbe occupied by two short-form ation EMUs, EMUs with different form ation occupy the maintenance track in different ways. Taking the space compatibility and the EMU operation planas the constraints, and taking minim ization of the last EMU’s completion timeas the ob ject, the optim ization model of first-leve l maintenance plan in EMU depot is estab lished, and then, the o riginal problem is trans form ed in to a hybrid flow-shop scheduling problem with special process constraints, and se lf-adaptive genetic a lgorithm is used to solve the model. In the end, taking an EMU depot as an example, this paperva lidates the feasibility and e ffectiveness of the mode l and algorithm.

EMU Depot; First-Leve l Maintenance; Hybrid Flow-Shop; Genetic Algorithm

1003-1421(2016)08-0059-07

U266.2；U269

A

10.16668/j.cnk i.issn.1003-1421.2016.08.11

2016-03-01

国家自然科学基金项目 (U 1434207)；中国铁路总公司科技研究开发计划课题 (2013X014-C)；中华人民共和国交通运输部交通运输科研经费研究项目 (2015-2-3)