“降维”技术在多变量综合评价中的应用
——基于TOPSIS和GRA的实证检验
2016-12-02李兴国张莉莉
李兴国,张莉莉
(燕山大学 a.高等教育发展研究中心;b.监察审计处,河北 秦皇岛 066004)
“降维”技术在多变量综合评价中的应用
——基于TOPSIS和GRA的实证检验
李兴国a,张莉莉b
(燕山大学 a.高等教育发展研究中心;b.监察审计处,河北 秦皇岛 066004)
“降维”是多元统计分析中对具有相关性和重叠性信息原始变量进行简化的一种方法,降维后的抽象变量能够保留众多原始变量的主要信息。通过将降维的思想扩展到多变量综合评价技术,选取2012年河北省各城市代表性经济指标数据,对降维前后的TOPSIS和GRA方法排序结果进行实证检验。结果表明:降维后的TOPSIS法与降维前的排序结果在0.01水平上显著相关,且相关系数高达0.9以上;降维后的GRA法与降维前的排序结果完全一致。表明降维方法在多变量综合评价与决策中具有良好的应用前景。
降维;多变量评价;因子分析;TOPSIS;GRA
多变量经济综合评价处理的是多变量问题,由于变量较多,增加了分析问题的复杂性。但在实际问题中,变量之间可能存在一定的相关性。因此,多变量中可能存在信息的重叠。人们自然希望通过克服相关性和重叠性,用较少的变量代替原来较多的变量,而这种替代可以反映原来多个变量的大部分信息,这即是一种“降维”的思想。因子分析(factor analysis)是一种降维、简化数据的技术[1]。这种降维的思想是否可扩展与应用到其他多变量综合评价方法之中,在保证决策效果的基础上,使分析计算的工作量得到简化?本文将通过因子分析降维得到的公因子应用到TOPSIS和GRA决策中,以解答上述疑问。
一、文献综述
关于多元统计分析方法在多变量综合评价中应用的相关研究成果目前还较为缺乏,笔者只找到寥寥数篇文献,研究思路主要集中在三个方面:一是主成分方法与TOPSIS法相结合,如邵景波、李柏洲、周晓莉在应用主成分分析法求得主成分决策阵的基础上,运用 TOPSIS 法进一步将低维系统降为一维系统,进而构造出加权主成分TOPSIS价值函数模型,并利用该模型对中国和俄罗斯的科技潜力进行了评价和比较分析[2];二是主成分方法与灰色关联分析相结合,如赵文英首先运用主成分分析计算黑龙江省13个地级市(区)11项原始指标的主成分得分,然后通过计算主成分得分与理想数据列样本主成分得分的灰色关联度,对各地区的城镇化水平进行排序和综合评价[3],童营营、金哲植利用主成分和灰色关联度相结合的方法,选取评价农民生活水平的指标因素,构建农民生活水平的指标体系,对8个省份的农民生活水平进行分析和排序[4];三是因子分析与灰色关联分析相结合,如刘宗鑫、王广杰、王群首先利用因子分析法得出四川省21个市(州)可持续发展能力综合得分,继而以综合得分为母序列,以各项统计指标数据作为子序列,计算二者的灰色关联度,进而得出各项评价指标重要度的排序结果[5]。
以上研究虽然在将多元统计分析方法应用于多变量综合评价方面作了一些初步的探索,但尚不系统和深入,尤其是在具体应用中,多是先利用主成分分析或因子分析得出评价对象主成分或主因子得分,而后再将评价得分运用到TOPSIS或灰色关联分析,没有体现出“降维”的优点。本文将弥补现有研究的不足,再将因子分析和TOPSIS、GRA的融合应用方面作进一步探索和尝试。
二、研究方法简介
(一)基于主因子的TOPSIS方法
1.基本思想
TOPSIS法是C.L.Hwang和K.Yoon于1981年提出的一种适用于根据多项指标对多个研究对象进行比较评价的统计方法[6]。基于主因子的TOPSIS法的思路是首先运用因子分析降维,将多维空间转化为低维空间,继而应用TOPSIS方法进行评价。
2.基本步骤
(1)收集原始数据。假设待评价对象为n个,使用的评价指标为p个,这组数据就构成了一个n×p矩阵。
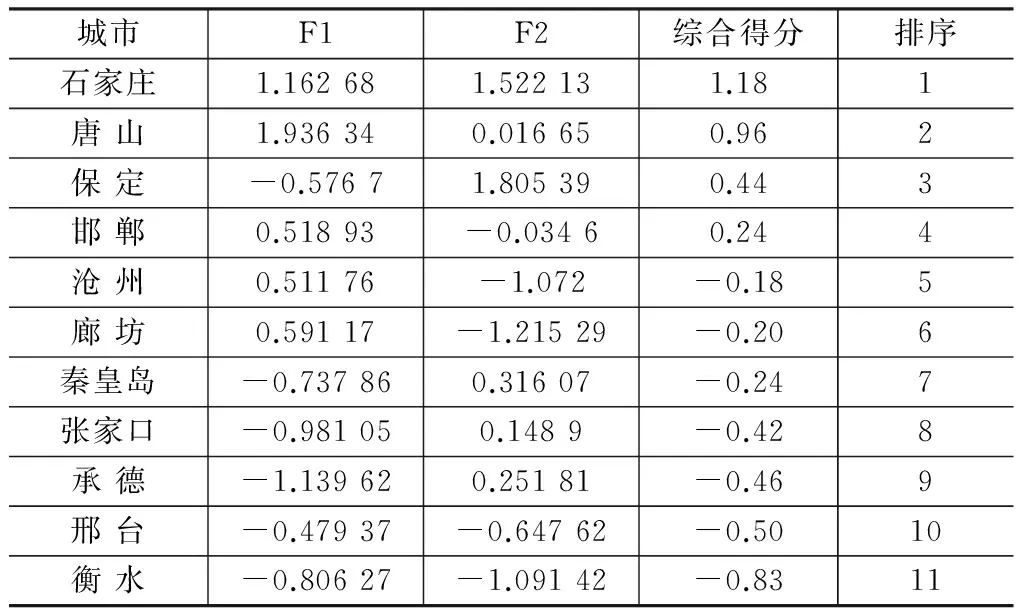
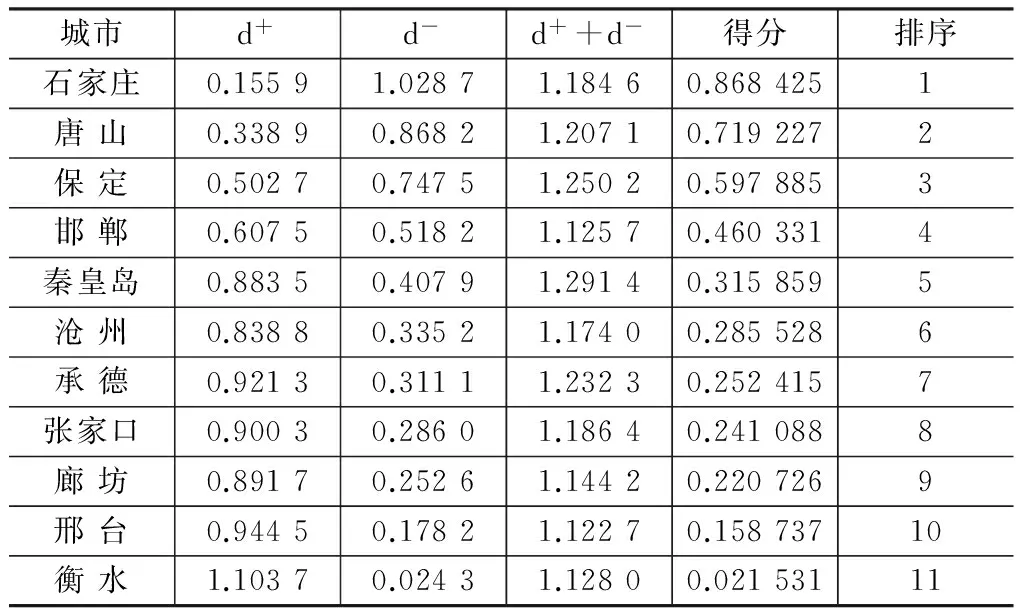
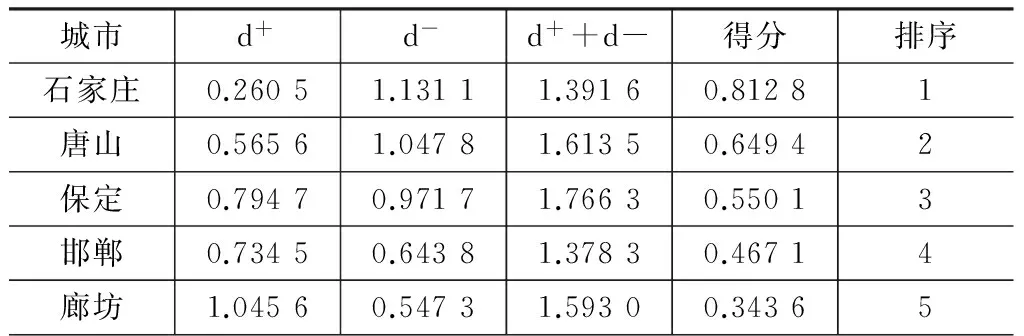
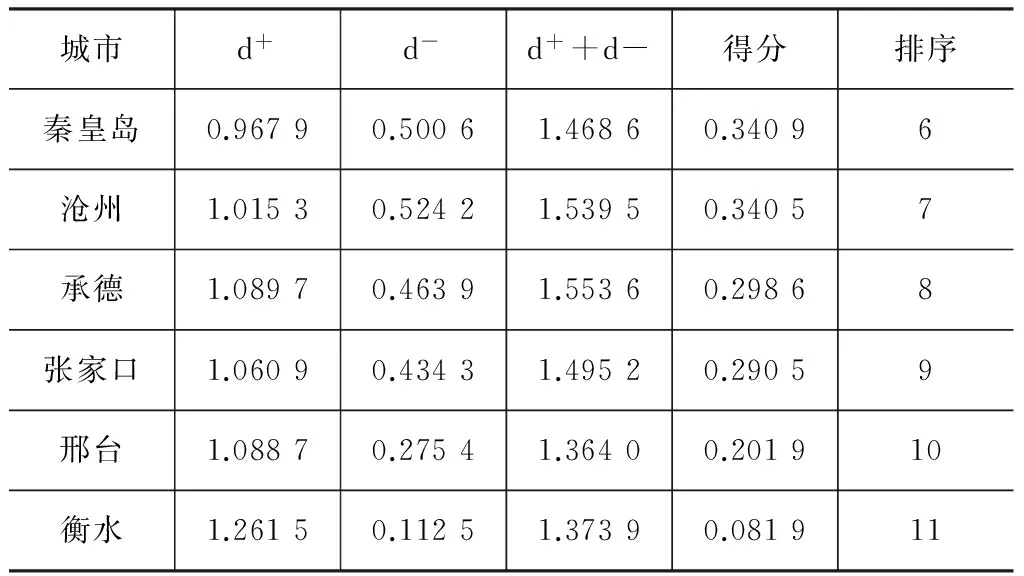
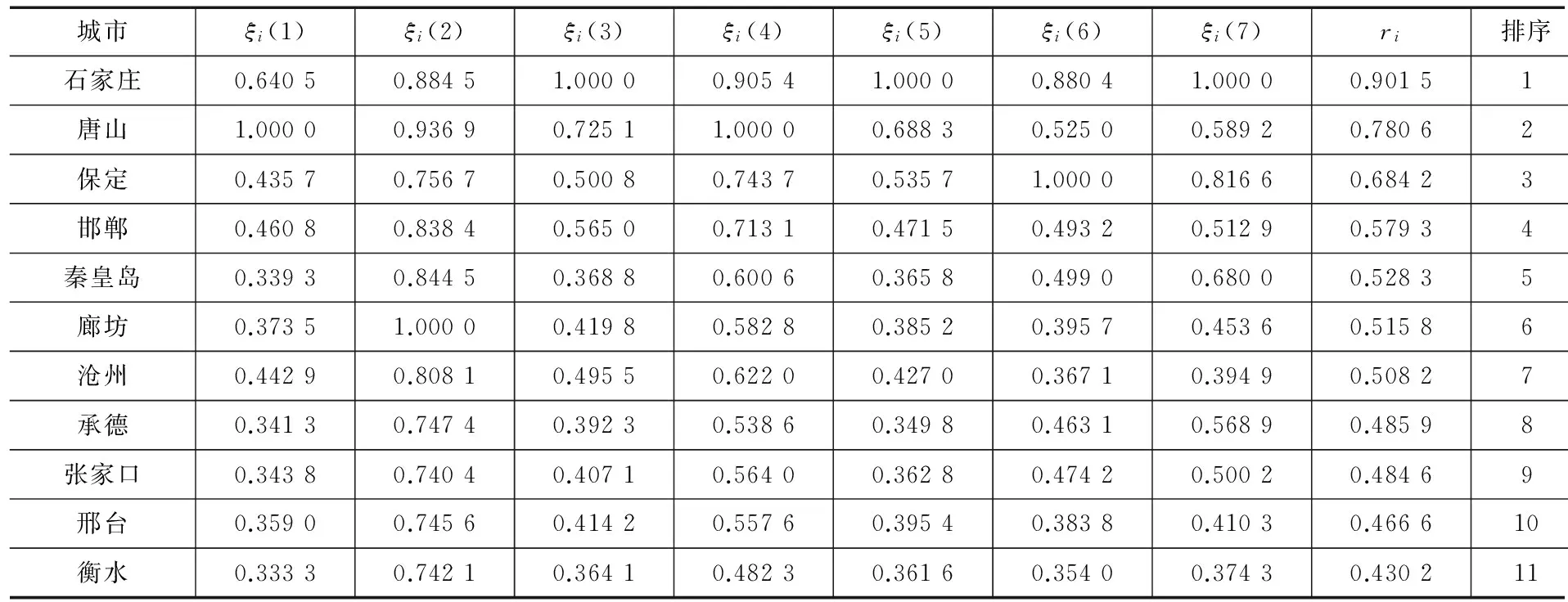
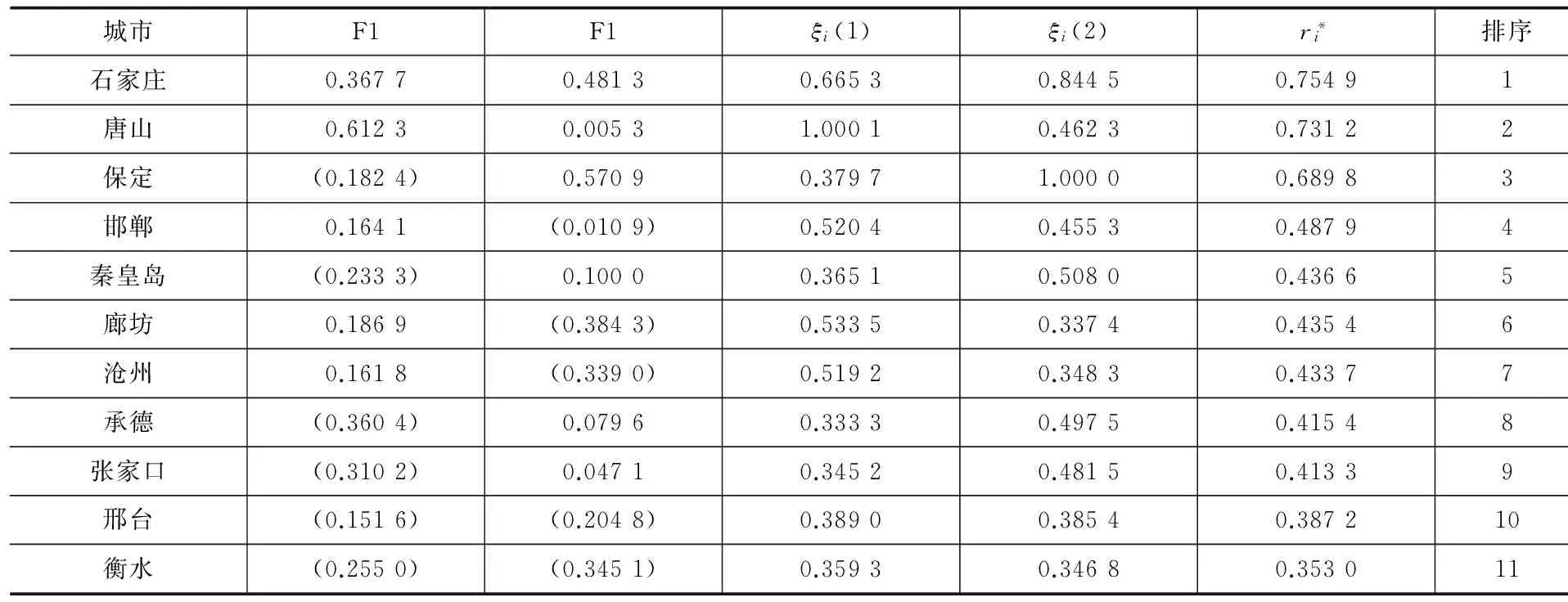
(2)因子分析。根据原始数据矩阵,计算原始变量的相关系数矩阵,进行因子分析适用性检验,得出因子载荷阵的特征根和方差贡献率,然后进行因子旋转和命名,得出m个(m (3)指标同趋势化处理。评价指标中有的是正指标,有的是逆指标,评价时要求都具有相同的趋势,一般把逆指标转化为正指标,转化方法可以采用倒数法(即1/x),多适用于绝对数指标;差值法(即1-x),多适用于相对数指标。 (5)根据标准化矩阵Znm,确定指标的正理想值和负理想值。 (6)采用欧几里得距离公式,计算各评价对象指标值与正理想解和负理想解的距离: 其中ωj为第j个评价指标的权重,如果各指标权重相等,ωj=1。 (7)计算各评价对象指标值与理想值之间的相对接近程度: 按接近度大小对评价对象的优劣进行排序。0≤Ci≤1,Ci越大表明评价对象越接近正理想解,越远离负理想解;Ci越小表明评价对象越接近负理想解,越远离正理想解。所以,Ci越接近1,则相应的评价对象就越应该排在前面。 (二)基于主因子的GRA 1.基本思想 灰色系统是邓聚龙教授在20世纪80年代初提出的适用于解决“少数据、贫信息”不确定性问题的一种评价方法[7]。灰色关联分析是根据序列曲线几何形状的相似程度来判断不同序列之间的联系是否紧密,曲线几何形状越接近,相应序列之间的关联度就越大,反之就越小[8]。基于主因子的GRA法的思路是首先运用因子分析降维,将多维空间转化为低维空间,继而应用GRA方法进行综合评价。 2.基本步骤 (1)因子分析。假设有n个评价对象,每个评价对象有p个评价指标。首先应用因子分析降维,得出m个主因子得分,将原始的n×p矩阵降为n×m矩阵,然后对降维后的n×m矩阵进行灰色关联分析。 (2)确定参考评价指标(参考数据列): {X0}={x0(1),x0(2),…x0(n)} 从上述数列选最优,或者选标准值。 (3)计算各评价对象指标与参考指标间的关联系数: (k=1,2…,n;i=1.2,…,m) α为分辨系数,0≤α≤1,一般取α=0.5。 (4)灰色关联系数矩阵: (5)计算灰色绝对关联度: (一) 研究对象 本研究选取2012年河北省各地级城市的地区生产总值X1(亿元)、人均可支配收入X2(元)、固定资产投资额X3(亿元)、财政支出额X4(亿元)、消费品零售总额X5(亿元)、全年接待游客总人次X6(万人)、旅游业总收入X7(亿元)等七个经济指标,并采集了原始数据。 (二) 因子分析过程 1.因子分析适用性检验。主要通过KMO检验和巴特利特球度检验来验证。KMO值为0.708,Bartlett检验结果的相伴概率为0.000,变量共同度多数在0.9以上,表明原始数据信息存在较大的相关性,适合进行因子分析。 2.公共因子特征值和方差贡献率。第一公因子的贡献率为49.132%,第二公因子的贡献率为40.155%,前两个公共因子的累计方差贡献率达到89%以上。 说明提取前两个公因子时,已提取了原始变量的绝大部分信息。因此,本文提取前两个主因子,并得到因子载荷矩阵。 3.因子旋转。为使各个因子的意义更加清晰,运用最大方差旋转法对因子载荷矩阵进行旋转,使各变量在某单个因子上有较高载荷,在其他因子上只有小到中等载荷。 第一主因子F1在X1~ X5上有较大的载荷,这4项指标反映的是城市经济基础对旅游业的支撑作用,可命名为“经济支撑因子”。 第二主因子F2在X6、X7上有较大的载荷,这2项指标反映的是旅游业产出情况,可命名为“旅游产出因子”。 4.以公共因子的方差贡献率进行加权,得到综合得分函数,进而计算出各城市得分及排序结果,见表1所示。 (三)TOPSIS分析 1.初始TOPSIS分析。按照上文所述方法,应用Excel编辑公式对表1中的数据进行TOPSIS分析,得到河北省各城市排序结果如表2所示。 表1 因子得分排序结果 表2 初始TOPSIS分析排序结果 2.降维TOPSIS分析。将上文因子分析所得的两个公共主因子F1和F2作为评价对象的新评价指标。如此,评价指标由原来的7个减少为2个,评价矩阵由原来的11×7阶简化为11×2阶,计算的工作量也大为减少。对新的评价数据矩阵进行TOPSIS分析,得到各城市排序结果如表3所示。 3.两种方法结果比较。对比表2和表3中的排序结果,发现前4个城市:石家庄、唐山、保定和邯郸的排序相同,分列第1~4名;最后两个城市邢台和衡水排序也一致。排序不同的是位于中间的5个城市。从相对位置来看,秦皇岛、沧州、承德和张家口等四市排序一致。排序结果最大的差异是廊坊,初始TOPSIS法将其排在第9名,降维后的TOPSIS法将其排为第5名。对两种排序结果进行Kendall和Spearman秩相关分析,发现两者在0.01的水平上显著相关,且相关系数高达0.9以上。 表3 降维后TOPSIS分析排序结果 续表3 (四)GRA分析 1.初始的GRA分析。按照上文所述方法,应用Excel对表1中的数据进行灰色关联分析,得到河北省各城市排序结果如表4所示。 2.降维GRA分析。将上文因子分析所得的两个公共主因子F1和F2作为评价对象的新评价指标。对简化后的11×2阶矩阵进行灰色关联分析,得到各城市排序结果如表5所示。可见,降维后GRA排序结果与未降维的GRA排序完全一致,但计算工作量却大为减少。 表4 初始GRA排序结果 表5 降维后GRA排序结果 (五)降维前后排序结果相关分析 1.对TOPSIS法而言,降维后的TOPSIS法排序结果与未降维的TOPSIS排序结果在0.01的水平上显著相关,Spearman秩相关系数高达0.909。从与因子分析、灰色关联分析排序结果的比较来看,降维后的TOPSIS法与其他两种方法评价结果相关性更高。从降维前后排序差别最大的样本“廊坊”来看,未降维的TOPSIS法将其排在第9名,降维后的TOPSIS法将其排在第5名,因子分析、降维前后的GRA方法均将廊坊排在第6名。可见,降维后的TOPSIS法由于克服了原始评价指标间相关性造成的评价信息重复问题而有效改进了评价结果。 2.对GRA方法,降维前后的GRA方法对11个评价对象的排序结果完全一致,但是降维后的计算工作量却大为减少。可见,降维方法在灰色关联分析中同样具有良好的应用前景。 表6 多变量综合评价方法排序相关性分析 本文以TOPSIS和GRA方法为例,通过实证分析,验证了“降维”作为多元统计分析中的一种方法,在保证决策结果基本一致的情况下,可极大地简化计算工作量,从而在多变量综合评价与决策领域具有广阔的应用空间。探索降维方法是否可以扩展到更多综合评价方法及降维对评价过程的影响机理,将是下一步研究的方向。 [1]朱建平,殷瑞飞.SPSS在统计分析中的应用[M].北京:清华大学出版社,2007. [2]邵景波,李柏洲,周晓莉.基于加权主成分 TOPSIS价值函数模型的中俄科技潜力比较[J].中国软科学,2008(9):132-139. [3]赵文英.基于主成分——灰色关联度的黑龙江省城镇化水平综合评价[J].数学的实践与认识, 2014(6):43-50. [4]童营营,金哲植.基于主成分——灰色关联度的农民生活水平评价[J].安徽农业科学, 2015(3):328-330. [5]刘宗鑫,王广杰,王群,等.基于因子分析和灰色关联度分析的区域可持续发展能力建设研究[J].安徽农业科学,2015(1):376-380. [6]刘辉,陈以增.一种基于模糊TOPSIS的采购商综合评价模型[J].统计与决策,2014(16):46-48. [7]钱吴永,李晓钟,王育红.灰色关联动态多指标评价模型及其应用[J].统计与决策,2014(24):7-10. [8]洪晓枝,冯鹤林.灰色关联度量化模型的改进[J].统计与决策,2014(9):80-83. (责任编辑 朱春花) Application of "Dimensionality Reduction" Technique in Multivariate Analysis Evaluation: An Empirical Test Based on TOPSIS and GRA LI Xing-guoa,ZHANG Li-lib (a.Higher Education Development Research Center of Yanshan Universiey; b.The Superrision of the Quditing Office of Yanshan University,Qinhuangdao 066004, Hebei, China) "Dimension reduction" is a method in multivariate statistical analysis to simplify the original variable of correlation and overlaps information.Abstract variables getting in dimension reduction can retain the main information of original variables.In this paper, we expand the idea of dimension reduction to multi-objective comprehensive evaluation technology,selection of typical economic index data from city in Hebei Province in 2012,carried on the empirical test before and after the dimension reduction of TOPSIS and the GRA method sorting result.The results showed that the reduction of TOPSIS method and dimension reduction before sorting result in significant correlation at the 0.01 level,and the correlation coefficient is as high as 0.9.The reduced GRA method is completely consistent with the prior sorting result which proves that the dimensionality reduction method has a good application prospect in multivariable comprehensive evaluation and decision. dimension reduction;multivariate comprehensive evaluation;factor analysis;TOPSIS;GRA 2016-07-22 2015年河北省文化艺术科学规划项目“河北省文化产业竞争力提升动力机理与实现路径研究”(HBWY2015-Y-F007) 李兴国(1981- ),男,河北邢台人,燕山大学高等教育发展研究中心助理研究员,经济管理学院博士研究生,主要从事管理科学与工程研究;张莉莉(1982- ),女,河北秦皇岛人,燕山大学监察审计处助理研究员,硕士,主要从事高校行政管理研究。 F207 A 1674-3571(2016)06-0047-05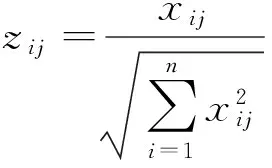
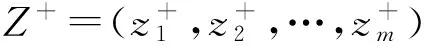
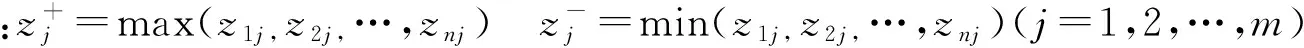
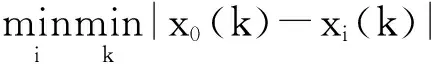
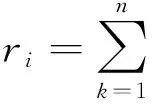
三、实证研究

四、结论
