“勾股分割点”尽压群芳，独放光彩——2015年浙江省台州市中考卷压轴题亮点赏析

●丁福珍

(天台县教育局教研室 浙江天台 317200)



“勾股分割点”尽压群芳，独放光彩
——2015年浙江省台州市中考卷压轴题亮点赏析

●丁福珍

(天台县教育局教研室 浙江天台 317200)

题目 定义：如图1，点M，N把线段AB分割成AM，MN和BN．若以AM，MN，BN为边的三角形是一个直角三角形，则称点M，N是线段AB的勾股分割点．

1)已知点M，N是线段AB的勾股分割点，若AM=2，MN=3，求BN的长.

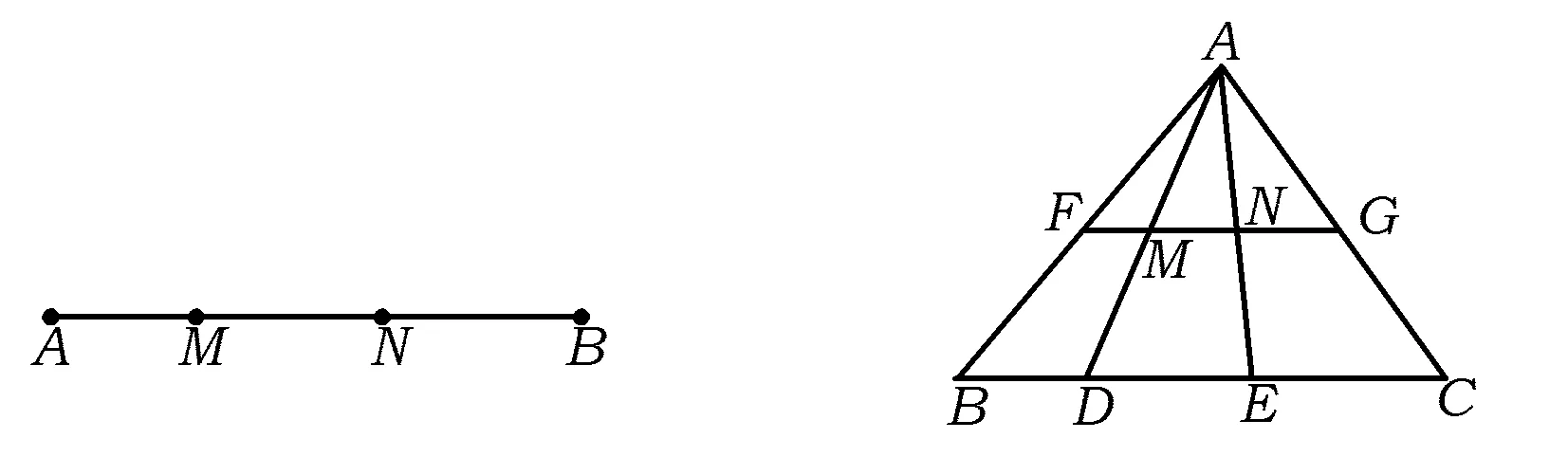
图1 图2

2)如图2，在△ABC中，FG是中位线，点D，E是线段BC的勾股分割点，且EC>DE≥BD，联结AD，AE分别交FG于点M,N．求证：点M，N是线段FG的勾股分割点.

图3 图4

3)已知点C是线段AB上的一定点，其位置如

图3所示，请在BC上画一点D，使点C，D是线段AB的勾股分割点(要求尺规作图，保留作图痕迹，画出一种情形即可).

4)如图4，已知点M，N是线段AB的勾股分割点，MN>AM≥BN，△AMC,△MND和△NBE均为等边三角形，AE分别交CM，DM，DN于点F，G，H，若H是DN的中点，试探究S△AMF，S△BEN和S四边形MNHG的数量关系，并说明理由．

(2015年浙江省台州市数学中考试题第24题)

本题作为压轴题，知识涵盖面广，综合程度较高，计算、作图、证明联手出击，融汇一体，彰显数学的本色.

亮点1 亲和力中融“四基”，体现公平

本题以学生熟悉的直角三角形以及勾股定理为背景，给学生一种“温暖”的心理暗示,倍感“平易近人”.通过文字语言描述、图形语言说明给出了“勾股分割点”的概念，在文字和图形的相互映衬下，学生能轻松地理解概念，消除了因不理解题意而无法解题的障碍.问题的呈现,从利用“勾股分割点”概念计算线段长度,再证明“勾股分割点”,最后进行尺规作图,进而综合应用“勾股分割点”寻求S△AMF，S△BEN和S四边形MNHG的数量关系,由易到难,层层递进,力求让不同层次的的学生在本题上会有不同的收获，真正诠释了《数学课程标准(2011年版)》中所提出的“学生要获得适应社会生活的基础知识、基本技能、基本思想、基本活动经验”，充分体现了试题的公平性.

亮点2 新颖度中藏“三技”，彰显本色

本题蕴藏数学的三大题型——计算、作图、证明，联手出击，融汇一体.《数学课程标准(2011年版)》中新增了关键词“几何直观”，就是在作图过程中，再现知识、熟练技能、历练思维，知识的来龙去脉全程展现，为巩固认知、加深理解提供了直观的感应和理性的思考.通览本题,命题者借助“勾股分割点”这个概念为载体,整个题目交汇于全等、相似等核心知识，计算、证明贯穿始终.第1)小题利用“勾股分割点”计算线段的长度，看似计算，实际上是理解与计算的凝聚,更是分类思想的渗透;第2)小题证明“勾股分割点”，是对新概念理解后的简单应用，促进学生能熟练掌握“勾股分割点”;第3)小题尺规作图，逆向思考，综合运用，提升学生的思维品质;第4)小题先猜想，再证明，难度大，凸显甄选功能.因此,“大胆猜想,细心求证”在本题中尘埃落定，成为考查学生逻辑思维能力的有效载体.

亮点3 解题法中赋“内涵”，回味无穷

《数学课程标准(2011年版)》中对“问题解决”的具体阐述是：“获得分析问题与解决问题的一些基本方法，体验解决问题方法的多样性，发展创新意识.”本题的第4)小题,解法多样,凸显本质,有利于引领学生学习能力的主动发挥和创造力的充分挖掘.下面就第4)小题提供几种解法供欣赏.

解 如图5，设AM=a，MN=b，NB=c.由H是DN的中点，得△MND，△BNE均为等边三角形，从而

△DGH≌△NEH.

因为

MG∥NE，

所以

即

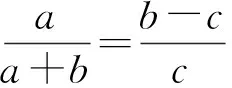
又因为

b2=a2+c2,

所以

(a-c)(b+a-c)=0,

即

a=c,

故

(此步骤是本题的关键，以下解法中将直接应用.)

方法1 利用相似比求面积

图5 图6

如图6，设FM=x，则

因为

AC∥MG,

所以

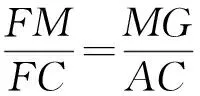
即

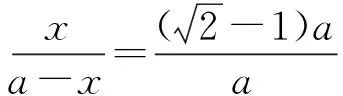
得

设S△AMC=S,则

即

则

故

于是

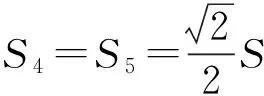
进而

因此

S1+S3=S2.

方法2 利用转化全等图求面积

如图7，过点E作EX∥BN，可证

S△AMF=S△XHE.

由

知

S梯形MNEG-S△HNE=S菱形NBEX-S△HNE,

即

S1+S3=S2.

图7 图8

方法3 利用等底同高分割面积

如图8，易证△ACF≌△GDH，于是AF=GH,从而

S△AFM=S△GHM.

因为H是DN的中点，所以

又因为

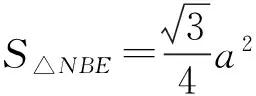
所以

S△MNH=S△NBE,

从而

S△AMF+S△NBE=S四边形MNHG.

方法4 利用全等分割面积

过点G作GK∥MN交DN于点K，因为

△ACF≌△GDH,

所以

AF=GH.

由

∠FAM=∠HGK， ∠AMC=∠GKH,

知

△AMF≌△GKH，

从而S四边形MNKG=S△MND-S△GKD=

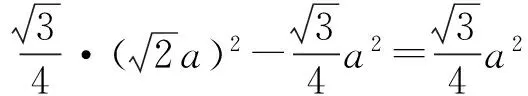
又因为

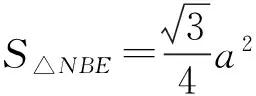
所以

S△AMF+S△NBE=S四边形MNHG.

图9 图10

方法5 利用中位线以及全等代换

如图10，取MN的中点P，联结HP，作HQ⊥NE于点Q.由PH∥NE得

从而 (b-a)(a-b+c)=0(其中a-b+c≠0)，

即

因为

△ACF≌△GDH≌△ENH，

且

所以

从而

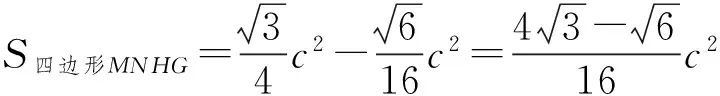
故

S△AFM+S△BNE=S四边形MNHG.

亮点4 区分度中蕴“灵动”，凸显选拔

图11

笔者在中考阅卷过程中,发现有许多考生的解题思路“火候”不够.笔者也曾迷惑,似乎其中有一定的道理,但通过仔细考究,发现这原来是命题者的“点睛之作”——凸显选拔性.

猜想 如图11，S四边形MGHN≥S△AFM+S△BNE.

简略理由如下：设AM=a，MN=c，BN=b.易证

△DGH≌△NEH， △ACF∽△DGH.

从而

因为

MN>AM≥BN,

即

a≥b,

所以

S△ACF≥S△DGH.

又因为

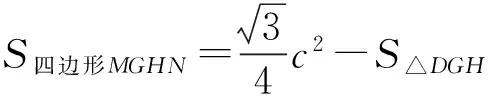
所以

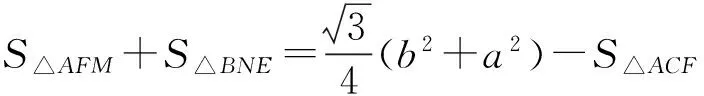
且

当a=b时，S四边形MGHN=S△AFM+S△BNE;当a>b时，S四边形MGHN>S△AFM+S△BNE.

综上所述,S四边形MGHN≥S△AFM+S△BNE.

这些考生的思维方式是到位的,但“火候”不够，因没有证明a=b而失分，足见命题者对第4)小题的深度思考和敏锐的洞察力.数学猜想需要经历特定的思维过程,看似简单的答案,却能考查学生的观察能力和归纳能力,考查学生是否具备丰富的知识储备、完善的认知结构.数学猜想作为综合程度很高的数学能力,具有科学性、多样性、假定性、验证性、创新性.因此,本题对新课程所倡导的核心理念——“一切为了学生的发展”作了真正的解读,无愧为一道妙题.