中高考交汇 2题共同源——2015年一道高考题与一道中考题解法探索

●杨 虎

(礼县职业中等专业学校 甘肃礼县 742200)



中高考交汇 2题共同源
——2015年一道高考题与一道中考题解法探索

●杨 虎

(礼县职业中等专业学校 甘肃礼县 742200)

自进入6月以来，高考、中考、小考等各级考试便接连不断，因此6月被称为“考试月”.经过“考试月”的洗礼，莘莘学子便有到更高一级学校深造的机会，同时“考试月”也是对教师的一场洗礼，通过对试题的学习与研究、反思与归纳，为今后的教学积累经验不无裨益.通过研习2015年的高考题和中考题发现，全国数学高考新课标卷文科的第22题(例1)与浙江省湖州市数学中考第20题(例2)有着惊人的相似，从而引起笔者的学习兴趣.下面就这2道题的学习与解法探索过程作一呈现，与各位数学爱好者分享交流.

1 原试题与参考答案

例1 如图1,AB是⊙O的直径，AC是⊙O的切线，BC交⊙O于点E.

1)D为AC的中点，求证：DE是⊙O的切线；

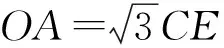
(2015年全国数学高考新课标文科试题第22题)

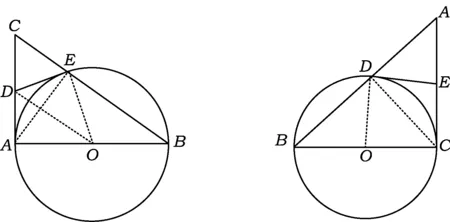
图1 图2

1)证明 联结AE，OE，由已知得AE⊥BC，AC⊥AB.在Rt△AEC中，由已知得DE=DC，从而

∠DEC=∠DCE.

又因为∠ACB+∠ABC=90°，∠OBE=∠OEB，所以

∠DEC+∠OEB=90°，

即

∠OED=90°，

故DE是⊙O的切线.

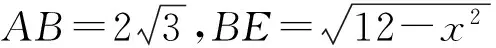
AE2=CE·BE，

从而

解得

于是

∠ACB=60°.

例2 如图2，BC是⊙O的直径，AC切⊙O于点C，AB交⊙O于点D，E为AC的中点，联结DE.

1)若AD=DB，OC=5，求切线AC的长;

2)求证：DE是⊙O的切线.

(2015年浙江省湖州市数学中考试题第20题)

1)解 联结CD.因为BC是⊙O的直径，所以∠BDC=90°，即

CD⊥AB.

又因为AD=DB，所以

AC=BC=2OC=10

2)证明 联结CD.因为∠ADC=90° ，E为AC的中点，所以

于是

∠CDE=∠DCE.

又因为∠ODC=∠OCD,AC切⊙O于点C(即AC⊥OC)，所以

∠CDE+∠ODC=∠DCE+∠OCD=90°,

故DE是⊙O的切线.

2 试题的交汇

2.1 一样的题干，相同的源头

通过仔细阅读这2道题，比较后发现题干部分基本相同，只是图形的字母有所不同，其源头都是平面几何中的圆与直线的问题，主要考查圆及其切线的相关知识与运算.其交汇点是例1的第1)小题与例2的第2)小题条件一样，问题也完全一样，都是求证DE是⊙O的切线，也就是证明直线DE与圆的半径OD垂直的问题.下面以例1的第1)小题为例进行解法探索.

探索1 利用2个角互余证垂直

证法1 如图3，联结AE,OE.因为AC是⊙O的切线，所以

∠CAE+∠OAE=90°.

又OA=OE，从而

∠OAE=∠OEA.

因为AB为⊙O的直径，D为AC的中点，所以

DE=DC=DA，

从而

∠DAE=∠DEA,

即

∠CAE=∠DEA, ∠DEA+∠OEA=90°，

亦即DE是⊙O的切线.

评注 证明2个角互余的方法很多，原题的参考答案也是利用2个角互余来证明垂直的，即通过证明∠DEC+∠OEB=90°得出∠OED=90°.而这里利用∠DEA+∠OEA=90°得出∠OED=90°，进而说明DE是⊙O的切线.

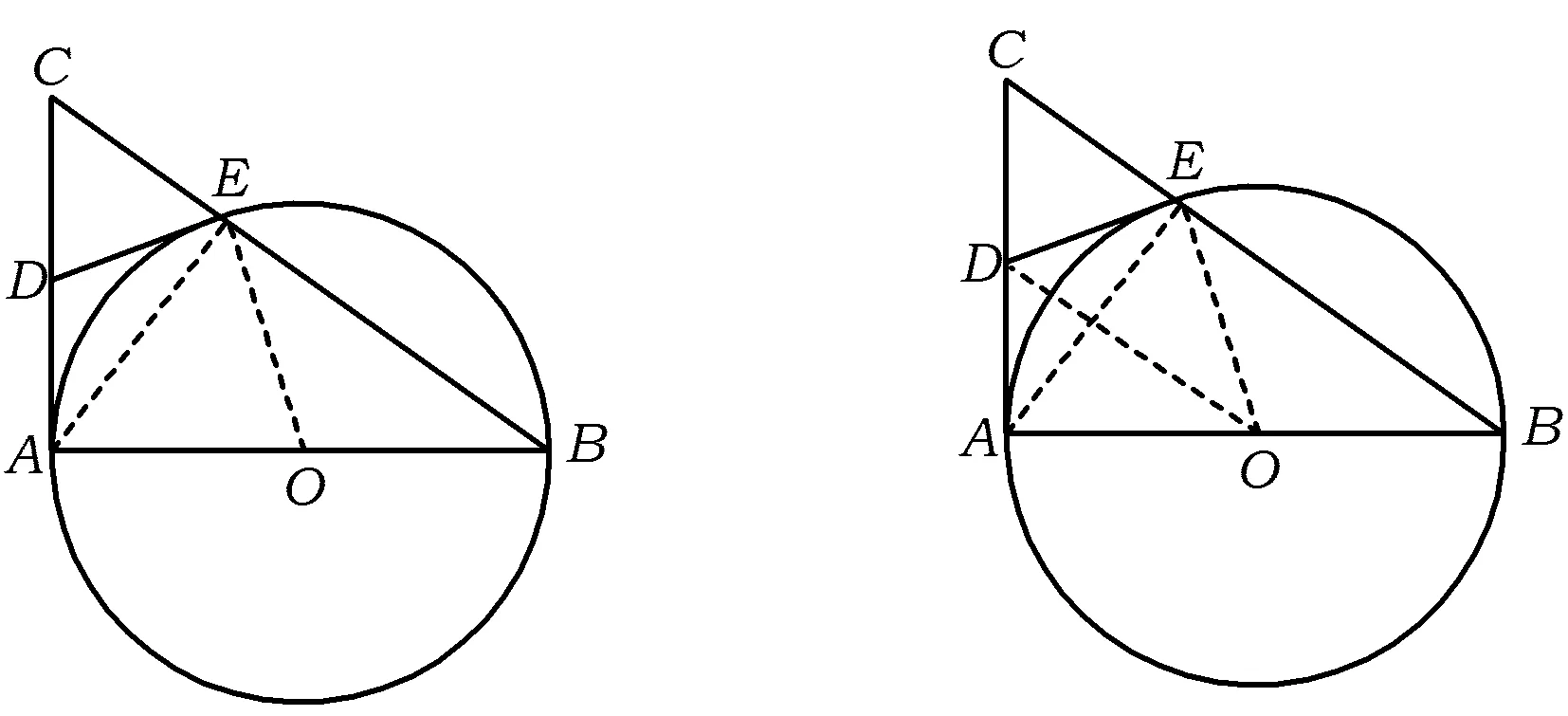
图3 图4

探索2 利用2个三角形全等证垂直

证法2 如图4，联结AE，OE,OD,易知DA=DE.因为CA是⊙O的切线，所以

∠CAB=∠DAO=90°.

易证△DAO≌△DEO,从而

∠DAO=∠DEO=90°，

因此DE是⊙O的切线.

评注 由于CA是⊙O的切线，从而∠DAB=90°，结合三角形的全等可证得∠OED=90°，达到证明的目的.

探索3 利用2个三角形相似证垂直

证法3 因为CA是⊙O的切线，所以

∠CAB=90°.

△DEO∽△CAB,

因此

∠DEO=∠CAB=90°，

故DE是⊙O的切线.

评注 在证明角相等时，相似也是一种很好的选择，此方法通过利用相似三角形，证明∠DEO=∠CAB=90°，达到证明的目的.

探索4 利用4点共圆证垂直

证法4 因为CA是⊙O的切线，所以

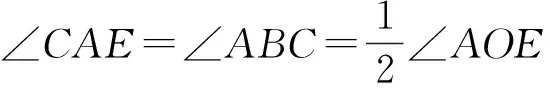
即

∠AOE=2∠CAE.

易得DA=DE,从而

即

∠CDE=2∠CAE，

于是

∠CDE=∠AOE,

因此点O,A,D,E共圆，从而

∠DAO+∠DEO=180°.

又因为∠DAO=90°，所以

∠DEO=90°，

故DE是⊙O的切线.

评注 4点共圆在平面几何中有重要的应用，在这里通过四边形的外角等于它的内对角来判定点O,A,D,E共圆，再利用4点共圆的性质，对角互补，达到证明的目的.

2.2 不一样的条件，相同的内涵

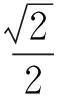
2.2.1 例1第2)小题的另解探索

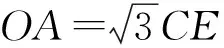
在Rt△ABC中，AB2+AC2=BC2，即

AC2=BC2-AB2，

从而

CE·CB=BC2-AB2，

于是

从而

于是

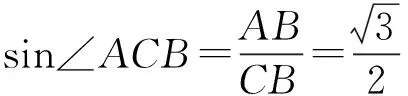
评注 由切割线定理及Rt△ABC中勾股定理的运用，结合方程思想，可以求得∠ACB的正弦值，从而求得∠ACB的大小.

2.2.2 例2第1)小题的另解探索

AE2=CE·BE，OC=OD=5,

从而

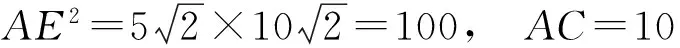
评注 正是因为这2道题有着紧密的联系，其内涵相同，所以通过分析例1的第2)小题便可以轻松地解决例2的第1)小题.

中、高考题凝结着命题人辛勤的汗水，体现了命题教师深邃的智慧.一道中考题与一道高考题有交汇，2题共同源，且出现在同一年的中考与高考题中，不失为一道亮丽的“风景”.放眼2道试题，通过对比学习、探索思考，这一道“风景”强烈的撞击着我们的思维，引领我们以不同的视角来审视问题，带给我们不同的体验，领略到不同的“风景”，让我们快乐在数学解题之中，陶醉在数学探索之中！