课堂中如何更好地发挥例题的作用——例题的引申与拓展例谈

●王常斌

(青云中学 广东佛山 528313)



课堂中如何更好地发挥例题的作用
——例题的引申与拓展例谈

●王常斌

(青云中学 广东佛山 528313)

高三复习的教学离不开选题，而高考题是我们选题的主要来源之一.选好例题固然重要，而在课堂上如何用好例题则更为重要.笔者在一节复习课中深刻体会到这一点，现将课堂实录整理出来，供同行参考.

本节课复习圆锥曲线及其应用，在简单复习完圆锥曲线的有关知识点后，笔者给出了一道例题：

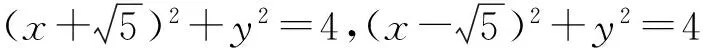
1)求⊙C的圆心轨迹L的方程；

本题选自一道高考题，笔者让学生尝试做第1)小题，会做的独立思考，有困难的看以下提示：

①你能画出2个已知圆吗？

②你能画出满足条件的一个⊙C吗？

③设⊙C的半径为r,你能用r表示出CF′与CF吗？

④由③你发现了什么？你能解决第1)小题吗？

设计意图 分层教学思想：能力强的学生独立解决；学困生在教师的问题提示下更好地理解题意，一步步找出解决问题的“源”.

图1

几分钟后生1上台板书：

则 ||CF|-|CF′||= |(r+2)-(r-2)|=

师：生1做得对吗？

生2：我觉得他的解答过程有问题，漏写了1种情况.

师：你能更正吗？

生2：可以.

于是生2上台将解答更正为：

从而 ||CF′|-|CF||= |(r+2)-(r-2)|=

笔者对2位学生都给予了肯定，特别是生2的思维严谨，并指出如果按生1的解答应是双曲线的一支，而不是完整的双曲线.笔者利用这个契机强化了双曲线的定义，在这里采用了概念复习习题化的方法，比单纯复习概念效果要好.接着，笔者让学生继续思考第2)小题如何解决，有困难的同学看以下提示:

①你能根据第1)小题计算的结果画出第2)小题的示意图吗？

②从示意图中可以看出点P，M，F构成什么图形？

③当点P运动到什么位置时，||MP|-|FP||最大？理由是什么？

设计意图 数形结合思想，从图中观察思考，启迪思维，教学着眼于学生的最近发展区，一步步引导学生找到解题思路.

(不一会，有学生发言.)

生3：我想应该用“三角形两边之和小于第三边”来做吧.

师：思路正确，那具体怎么做呢？

生3：我还未想好.

师：那同学们再思考一下，也可以相互讨论.

(不一会，另一位学生发言.)

生4：当点P,F,M共线时，||MP|-|FP||取得最大值，因此只需求出直线MF与双曲线的交点坐标即可.

师：三个臭皮匠，顶个诸葛亮！同学们按此思路试试看.

下面是生5板书的解答过程：

||MP|-|FP||≤ |MF|=

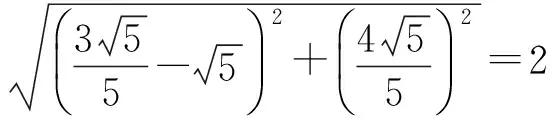
得

从而

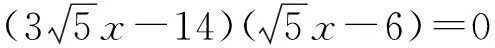
解得

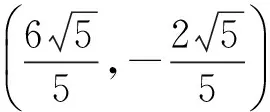
师：同学们，上述的解答过程有问题吗？

生6：不是2个点，而应舍去一个.

师：为什么？

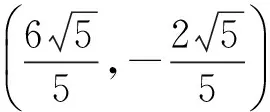
师：同学们明白了吗？可以自己画图试试.

图2

(学生们画出如图2所示的图形，得到验证后大家对生6佩服有加.)

教师趁热打铁：解析几何是用代数方法来解决几何问题，体现了数与形的结合，因此千万不要忽视形(图形)在解题中的作用啊!

(例1解决了，同学们都意犹未尽，笔者觉得就此打住未免太可惜了.)

师：同学们，我们不是为了解题而解题，要力争做到“做一题，会一类”.对于例1，能否改变其中的条件或所求问题而变出其他题目呢？请同学们试一试.

笔者让学生谈谈自己的改题方案.方案五花八门，有合理的，也有不合理的，经过筛选，综合起来合理的改题方案有以下几种：

变式1 1)将第1)小题中的条件“与一圆内切，与一圆外切”改成“与2个圆都外切”或“与2个圆均内切”.

2)在第1)小题中改变2个圆的位置关系.

3)将变式1),2)中的条件同时改变.

4)第2)小题中求|MP|+|FP|的最小值.

5)改变第2)小题中点M的位置，求|MP|+|FP|的最小值.

上面的变式1因为很简单，所以教师让学生直接说出答案：轨迹L的方程为直线x=0(其中y≠0).

然后，笔者让每个学习小组(4人一组)自选以上变式2)～5)中的1个进行探究.10分钟后，各小组派代表展示自己的探究成果(简单地书写在黑板上，例题书写量大的用草稿纸进行投影).当然在展示的过程中也有一些错漏，经过学生纠错和师生共同评定都予以更正.现选取学生的探究结论和部分例题整理如下：

变式2 1)由例1知，当2个圆外离时，与一圆内切、与另一圆外切的圆的圆心轨迹L为双曲线，2个圆半径不相等时此结论仍然成立.

2)当2个圆外切时，与一圆内切、与另一圆外切的圆的圆心轨迹L为一条直线(去掉3个点)，即2个圆的连心线(去掉2个圆的圆心及切点),2个圆半径不相等时，此结论仍然成立.

3)2个圆内切时，满足条件的轨迹为椭圆(去掉切点).

例2 设⊙C与2个圆(x+2)2+y2=1，(x-2)2+y2=25中的一个内切，另一个外切．求⊙C的圆心轨迹L的方程.

分析 设F′(-2,0)，F(2,0),⊙C的半径为r，因为⊙C只能与小圆外切与大圆内切，所以

则

|CF′|+|CF|=(r+1)+(5-r)=6>4,

4)当2个圆内含时，满足条件的轨迹为完整的椭圆.

变式3 1)当2个圆外离且2个圆半径不相等时，与2个圆均外切的⊙C的圆心轨迹为双曲线的一支.

2)当2个圆外切且2个圆半径不相等时，与2个圆均外切的⊙C的圆心轨迹为双曲线的一支(去掉2个圆的切点).

3)当2个圆相交且2个圆半径不相等时，与2个圆均外切的⊙C的圆心轨迹为双曲线一支的一部分(去掉夹在2个圆交点之间的部分(包括2个交点)).

当2个圆半径不相等时，与2个圆均内切的圆的圆心的轨迹与2个圆外切时有类似的结论，这里不再赘述.

分析 |MP|+ |FP|≥|MF|=

图3

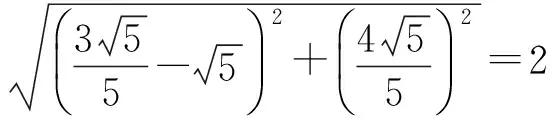
得

解得

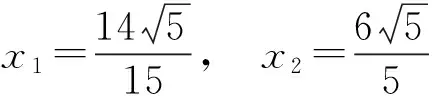
图4

分析 在例3中，点M夹在双曲线的2支之间，而由例4画出图形(如图4所示)可知，点M在右支里面，从而直线MF与双曲线的交点P不可能夹在点M,F之间，因此例4用例3的方法行不通.显然满足条件的点P只可能在右支上，可以考虑用双曲线的定义，将|FP|转化为|PF′|-4(其中F′为双曲线的左焦点)，从而转化为求|MP|+|PF′|-4的最小值，再用例3的方法解决.

|PF|=|PF′|-4，

从而 |MP|+|FP|= |MP|+|F′P|-4≥

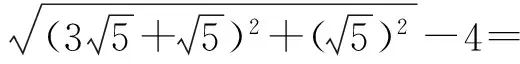
解得

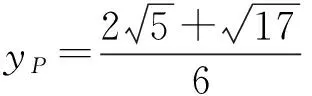
学生展示完探究结果，师生共同赏析和点评后，进入课堂小结环节.

师：今天我们解答了一道高考题，并对此高考题进行了改编，同学们改编出若干好题、妙题，探究出许多有意义的结论，看来同学们学习数学的潜力是无穷的！通过今天这节课的学习，你有哪些收获和体会，请自由谈谈.

(得到教师的表扬，每位学生都很开心，兴致更高.)

生7：今天我学会了用定义法求圆锥曲线的轨迹方程，其关键在于如何将题目中的条件转化为符合圆锥曲线定义的表达式.

生8：在求曲线轨迹方程时，要画出草图，分清与哪个圆内切，与哪个圆外切；利用2个圆的位置关系写表达式时，要结合草图来看.特别是2个圆内切时，一定要分清哪个圆的半径大、哪个圆的半径小.

生9：我觉得求出曲线方程后,还应该考虑自变量的取值范围.

生10：今天我学会了“已知2个点M,P的坐标，如何在已知曲线上求一点P，使得||MP|-|FP||取得最大值，或使得|MP|+|FP|取得最小值”.前者用“三角形两边之差小于第三边”，后者用“三角形两边之和大于第三边，3个点共线时取等号”.

生11：我觉得共线时取等号，还要考虑到点P的位置，前者应在MF的延长线上，后者在线段MF上.

生12：我觉得做解析几何题时一定要注意数形结合：前面求曲线方程时如此，后面求最值时也要画出草图；根据点M的位置来选择是直接求直线MF与曲线的交点，还是转化为求直线MF′与曲线的交点.

(以上学生们的发言，赢得了大家阵阵掌声，也得到了教师由衷的赞扬.接着教师布置了课后作业.)

师：每位同学将课内自己没有探究的变式，选择2～3个进行探究，每个变式自编一题，并写出详细的解答过程.

通过这节习题课的教学，笔者也有较大的收获.体会最深刻的一点是在课堂教学中，教师要充分发挥教学智慧，要创造条件充分发挥例题的辐射作用.许多教师对例题的教学仅停留在题目的表面，学完例题，做几道同类的练习题，但缺乏对解题方法的提炼、对解题策略的总结.学生仅停留在简单模仿或变式练习阶段，只有少数学生能从例题和练习中自发领悟.要使学生对所学的知识融会贯通，我们必须引领学生从“自发领悟”到“自觉分析”.对于选择的经典例题要善于“从不同的角度挖掘100次，这样的效果要远胜于对100道题只浅挖一次”[1].这就要求教师在课堂内多创设一些情景，多给学生一些平台，激发他们的好奇心和求知欲，充分发挥学生学习的自觉性、主动性.教师的“外因”必须通过学生的“内因”起作用，学生的有意义建构是例题教学的本质之所在.

[1] 王永生.一道高考数学试题教学运用的精彩故事[J].中学数学教学参考:上旬，2014(1/2):42-45.