等式基本性质教学设计的几个要点*

●王红权

(杭州市普通教育研究室 浙江杭州 310003)



等式基本性质教学设计的几个要点*

●王红权

(杭州市普通教育研究室 浙江杭州 310003)

“源于生活、易于理解”是对日常生活中的一些规律的最为简朴的抽象.等式基本性质是数学中的基本规律之一，小学和初中的教材中都呈现了该内容，它是数学基础教学中重要的教学内容，在教学设计中需要充分理解其地位、价值和意义.

1 理解等式的含义是“开篇设计”的前提

1.1 教材呈现以图代文，教学必需由图及文(数)

本文所指的教材是指浙江教育出版社义务教育教科书《数学》(七年级).“开篇设计”以实验形式呈现，符合学生的认知规律，让学生真实经历等式基本性质的形成过程.因此教学设计时必须要有实验操作环节，在图1、图3的基础上通过添加(或减少)相同的砝码个数(如图2、图4所示)，观察天平是否平衡，“触摸”等式基本性质1的生活原型.这个环节展示时要注意3点：1)演示要反复多次并能让学生注意到每一次操作都是“对称的”；2)要让学生体会到这种操作是“可逆的”(添加和取出)；3)要注意让学生思考操作过程中的不同状态：从一种平衡通过“操作”到另一种平衡，在这一变化过程中不变的是什么.

图1 图2

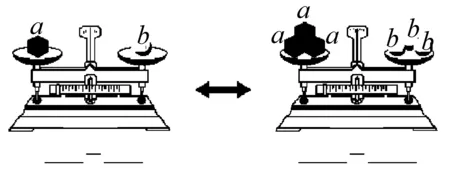
图3 图4

教材采用合作学习的方式，教师辅之以实验，目的都是为了让学生增加体验，获得经验，为接下来的抽象归纳提供直观的、感性的原型，使得数学抽象不再是无源之水、无本之木.

1.2 图是图，文是文，数学抽象是理性的抽象

1.3 反思一个案例

在某省级观摩课中，笔者发现几处课堂细节的发生与上述理解有密切的关系.第1个细节是教师演示完实验后学生在归纳形成等式基本性质2时，忽略了“c≠0”，原因就是教师强调了2组图中的“双箭头”，而忽视天平称量的可逆并不是数学原理的可逆，失去提升学生理性思考的绝佳机会.

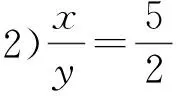
2 熟练运用等式基本性质是“中篇设计”的关键

学生凭借已有的生活经验理解等式基本性质应该不会困难，但熟练应用并在应用过程中提升其逻辑思维能力和提炼出解方程的依据需要对教材编排有深刻的理解.

等式基本性质教学单元的设置是为解一元一次方程服务的.由于在一元一次方程的解决过程中只涉及移项、去分母(分母不含0因子)和合并同类项，因此在等式性质教学设计时不必过分强调分母等于0的情形.一般而言，在等式基本性质2的应用举例教学设计时不宜补充如下问题：“已知2x-5y=0，且x≠0，求y与x的比”，留待学习分式时再研究.

3 等式基本性质、方程同解、分配律是“收官之篇设计”的三大支柱

利用等式基本性质可以解一元一次方程，其原因就是在对方程进行变形的过程中，方程本质属性不变.

1)同解方程：解集相同的方程(等价方程).例如方程x-2=0与方程x=2是2个同解方程.同解是方程之间的一种等价关系，可以用一个简单的同解方程来代替一个较复杂的方程.同解原理：①方程的2边加上同一个数或式(式与方程的定义域相同)，方程的解集不变.容易知道“移项”是一种同解变形.②方程的2边乘以同一个非0的数或不取零值的式(式与方程的定义域相同)，方程的解集不变.

当方程变形不满足同解原理时，变形后的方程就有可能出现增根或失根.因此在教学时必须注意利用等式性质解一元一次方程并不是没有原则的使用，是在利用由等式性质导出的“移项”、“去分母(这里指方程的2边同乘以或除以一个非0的数)”和乘法分配律解一元一次方程.这就是讲解例2需要渗透的关键点，也是对讲解“1例5练”所获得认识的理性提升和自然延续.

2)从同解原理中可以知道“移项”是同解变形；“去分母”时，方程的2边同时乘以或除以一个非0的数也是同解变形.这2条构成解一元一次方程的全部依据.由此看来“检验”一元一次方程的解是“多余”的，那么教材为何在例2之后编排“检验”？解读不好会对后续学习产生困惑，即学生不清楚到底什么时候需要检验方程的解(正常的解一元一次方程不会产生增根和失根)，什么时候不需要检验.教学设计时不必过分强调“检验”环节，知道通过“检验”可以判定解得的“解”是否正确就够了.原因非常简单：时候未到！等到学解分式方程并且增根出现时，在学生产生强烈的认知冲突时(增根从哪里来的)，分析强调教学效果会更好.当然更加不必去补充“体现所谓检验必要性”的例题了.

3)教材不涉及方程同解原理是为了突出基础数学的本质和基本思想都是平实朴素、平易近人的，但要教得平易近人需对教材作深入研究.表面上看方程中的“未知量”是不定元，实际上是一个未知量和已知量之间约定关系式中的待定量，是一个确定的数，因此它满足数的全部运算律.解代数方程的基本原理就是有系统地运用运算律把所给的代数方程简化，从而确定其中所含的“未知数”所应取之值[1].在简化一元一次方程的过程中使用“移项”和“去分母”等手段，其本身并不构成解代数方程的核心思想方法，通过这些手段需要表达的是可以通过系统的、程序化的方法达成化未知为已知的目的(算法思想的直接渗透).

由此可知，例2的教学中需要淡化等式性质的直接应用，要注重等式性质和“移项”、“去分母”的交替使用.不必过分强调等式性质的适用性，而要体验其中“以简驭繁，化未知为已知”的简朴道理，体验解决问题的系统性和规律性，也就是解决问题的程序性，让算法思想根植于学生的心中.设计好等式基本性质的教学，为进一步学习解方程提供最好的范本.

[1] 项武义．基础代数学[M]．北京：人民教育出版社，2004．

王红权，男，杭州市普通教育研究室中学数学教研员，中学高级教师，曾获杭州市教育系统优秀教师、教坛新秀、优秀党员，杭州市数学学科带头人，中国统计教育学会基础教育分会理事，浙江省数学会理事，浙江省教育学会中学数学分会常务理事，杭州市数学会秘书长.近年来主持浙江省、杭州市重点规划课题多项，获奖多项，参与国家社科、教育部重点课题多项，已在各类杂志发表论文50余篇．

本文是全国教育科学“十一五”规划2010年教育部重点课题“中小学数学核心内容及其教学的研究”(编号：G0A107010)及2014年浙江省教研课题“中学数学核心概念‘习得型’习题课教学设计研究”(编号：14B002)的研究成果之一．