一种用定积分证明泰勒中值定理的方法
2016-12-01张康宇吴茂全
张康宇, 吴茂全
(沈阳化工大学 数理系, 辽宁 沈阳 110142)
一种用定积分证明泰勒中值定理的方法
张康宇, 吴茂全
(沈阳化工大学 数理系, 辽宁 沈阳 110142)
介绍一种从拉格朗日中值定理出发,通过重复的定积分运算,直接推导出泰勒中值定理的方法.首先通过定义函数,将拉格朗日中值定理的表达式转化为可积的形式,之后在定义域的任一闭区间上对其进行定积分;得到的结果通过定义第二个函数再次转化为可积的形式,继续进行定积分.如此循环n-1次,得到一个类似于泰勒中值定理的n次多项式.通过对在定积分过程当中所定义的n个函数的值域进行讨论,便可将此n次多项式转化为泰勒中值定理的形式.这种方法不需要泰勒公式作为推导的基础,因此,它能较好地揭示泰勒中值定理的本质,建立泰勒中值定理与拉格朗日中值定理之间的有机关联.
拉格朗日中值定理; 泰勒中值定理; 定积分
1 问题的提出
泰勒中值定理与拉格朗日中值定理同是两个重要的微分学中值定理.仅从形式上看,拉格朗日中值定理是泰勒中值定理的特殊形式,文献[1]和文献[2]都提到了这一点.不过,正如文献[3]所表述的“泰勒定理不妨看成是拉格朗日中值定理在导数的阶数上的一个推广.”通过几何意义明确的拉格朗日中值定理引出并证明泰勒中值定理,显然有助于对泰勒中值定理的理解.
但是,文献[3]并没有给出一种直接由拉格朗日中值定理推广至泰勒中值定理的方法,而是与文献[1]、[2]和[4]中的方法的出发点相同,是在泰勒公式的基础之上,讨论了如何通过构造函数来证明泰勒中值定理.因此,本文以拉格朗日中值定理为基础,直接推导出泰勒中值定理.
2 对问题的讨论
设函数f(t)在区间(a,b)内有直到n阶的导数.任取t0∈(a,b),设t>t0,则由拉格朗日中值定理,在(a,b)上有
f(n-1)(t)-f(n-1)(t0)=
f(n)(ξ)(t-t0) (ξ∈[t0,t])
文献[3]中表述:“拉格朗日中值定理给出了函数与其一阶导数的关系,而泰勒定理却给出了函数与其高阶导数之间的关系.”因此,由拉格朗日中值定理推导泰勒中值定理的关键是:通过上式,得到f(n)(t)与f(t)的函数关系.若通过定积分运算可以使上式左端f(t)导数的阶降低,同时保持右端f(t)导数的阶不变,则重复对上式作n-1次的定积分运算,问题得解.
记f(n)(t)在其定义域(a,b)上的值域为M.任取(a,b)内一点t0,则由拉格朗日中值定理,对任一t∈(a,b),设t>t0,均存在ξ0∈(t0,t)⊆(a,b),使得
f(n-1)(t)-f(n-1)(t0)=f(n)(ξ0)(t-t0)
对于任一t≠t0,f(n)(ξ0)∈M由t唯一确定,故将区间(a,b)上的t与f(n)(ξ0)的函数关系记作


故h0(t)在t=t0处连续.记h0(t)在(a,b)上的值域为M0,显然M0⊆M.由于[f(n-1)(t)-f(n-1)(t0)]与(t-t0)均在(a,b)上连续,且h0(t)在t=t0处连续,故h0(t)在(a,b)上连续,并且在(a,b)的任一闭子区间上可积.由此,任取t∈(a,b),作第一次定积分
(1)
设t>t0,故在[t0,t]上,(s-t0)不改变符号,h0(s)连续.故由积分平均值定理[5],存在ξ1∈[t0,t],使得
故式(1)变为
f(n-2)(t)-f(n-2)(t0)-f(n-1)(t0)(t-t0)=
(2)
由于t为(a,b)上的任取值,而式(2)中的闭区间[t0,t]仅用作定积分运算,且[t0,t]⊆(a,b),故式(2)可写作
f(n-2)(t)-f(n-2)(t0)-f(n-1)(t0)(t-t0)=
(3)

由洛必达法则
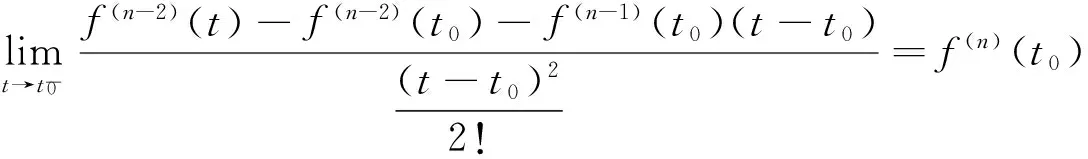

f(n-1)(t0)(s-t0))ds=
仿照上面的步骤,易得
(4)

由洛必达法则
f(n)(t0),
故h2(t)在t=t0处连续.记h2(t)在(a,b)上的值域为M2,显然M2⊆M1⊆M0⊆M,故式(4)可记作
仿照上面重复进行定积分,当进行了k次这样的定积分之后,将得到
其中,(a,b)上的连续函数hk(t)的值域为Mk,Mk⊆Mk-1⊆…⊆M0⊆M,故当k=n-1时,得到
(5)
其中hn-1(t)在(a,b)上的值域为Mn-1.由于Mn-1⊆Mn-2⊆…⊆M0⊆M,故对于任意t∈(a,b),必存在至少一个ξ∈(a,b),使得hn-1(t)=f(n)(ξ)∈M,因此,可将式(5)记作
(ξ∈(a,b))
此结果所表述的正是泰勒中值定理.
3 结 论
从上面的推导过程可以看出:本文的直接引出同时证明泰勒中值定理的方法与文献[1-4]中单纯证明泰勒中值定理的方法有着本质的不同.文献[1-4]中的方法,是在已知泰勒公式的具体形式的前提下,求出拉格朗日余项,从而证明定理.而本文的方法,是从拉格朗日中值定理出发,通过定积分层层还原,最终自然地得到泰勒中值定理,即证明了定理.
[1] 同济大学数学系.高等数学[M].6版:北京:高等教育出版社,2007:141.
[2] 吴纪桃,魏光美,李翠萍,等.高等数学[M].2版.北京:清华大学出版社,2011:112.
[3] 闵兰,陈晓敏.几个微分中值定理之异同:从罗尔定理到泰勒定理[J].西南师范大学学报(自然科学版),2009,34(6):197-199.
[4] 陆伟,刘佳依,王帅.泰勒中值定理的证明及应用探析[J].学园,2013(23):57-58.
[5] 常庚哲,史济怀.数学分析教程(上册)[M].3版.合肥:中国科学技术大学出版社,2012:246.
A Proof of Taylor′s Theorem Using Definite Integral
ZHANG Kang-yu, WU Mao-quan
(Shenyang University of Chemical Technology, Shenyang 110142, China)
With Lagrange′s theorem been treated as the starting point,a method includes repeated definite integral can work out Taylor′s theorem directly.Transform the expression of Lagrange′s theorem to make it integrable using the function defined in the first place.Then do the integral on any closed interval of the domain of definition; transform the result to make it integrable by defining the second function,then do the integral again.Cycle forn-1 times like this,an-order polynomial which is similar to the expression of Taylor′s theorem will be gained.By discussing the range of thesenfunctions,the polynomial can be transformed into the form of Taylor′s theorem.The Taylor′s formula is not the foundation of this method,so this method can reveal the essence of Taylor′s theorem,can build an organic relationship between Lagrange′s theorem and Taylor′s theorem.
Lagrange′s theorem; Taylor′s theorem; definite integral
2015-06-08
张康宇(1995-),男,江苏赣榆人,本科生在读,主要从事化学工程与工艺的研究.
吴茂全(1963-),男,河北冀县人,副教授,硕士,主要从事代数学、高等数学及工程数学的教学及科研研究.
2095-2198(2016)03-0275-03
10.3969/j.issn.2095-2198.2016.03.018
O13
A
