氮化锗多形体的四方、单斜和正交畸变的理论研究

仓玉萍, 陈 东, 杨 帆, 杨慧明

(信阳师范学院物理电子工程学院, 信阳 464000)



氮化锗多形体的四方、单斜和正交畸变的理论研究

仓玉萍, 陈 东, 杨 帆, 杨慧明

(信阳师范学院物理电子工程学院, 信阳 464000)

采用量子化学从头算方法, 对Ge3N4的四方、 单斜和正交结构同质异相体的微结构、 态密度和声子谱进行了研究. 形成焓为负值、 弹性常数满足Born稳定性准则和声子谱无虚频等结果证实在0～20 GPa范围内3种相都能保持结构稳定. 温度变化影响到晶胞体积, 从而使体模量发生改变. 3种Ge3N4都属于半导体, Ge原子和N原子之间存在明显的s-p杂化现象. 当压强增大时诱发了离域电子, 从而使体系的带隙减小. 本文还采用准谐近似对Ge3N4的热力学性质进行了研究, 结果表明, 温度和压强对热膨胀系数、 熵、 热容、 德拜温度和格林爱森参数产生了明显影响.m-Ge3N4和t-Ge3N4的热膨胀系数分别为o-Ge3N4的3倍和2倍.t-Ge3N4和o-Ge3N4的晶格谐振频率基本不受温度的影响.

从头算; 氮化锗; 电子结构; 稳定性

1 理论模型和计算方法

t-,m-和o-Ge3N4的晶胞结构如图1所示[26]. 本文采用量子化学从头算方法进行自洽总能量计算[27], 电子之间的交换关联势采用广义梯度近似(GGA)下的PBE泛函来描述[28]. 原子的价电子组态是N-2s22p3和Ge-4s24p2. 采用体系的总能量进行收敛测试, 收敛精度为5×10-7eV/原子. 平面波截断能设定为500 eV.c-Ge3N4,t-Ge3N4,m-Ge3N4和o-Ge3N4的布里渊区分别采用10×10×10, 12×12×8, 8×18×12和11×7×10的Monkhorst-Packk点网格来描述[29]. 在态密度计算时空带数目设定为43. 采用有限位移方法计算声子[30], 超晶胞的截断半径为0.5 nm.t-Ge3N4,m-Ge3N4和o-Ge3N4的q矢量分别设置为7×7×4, 5×9×6和6×6×8. 计算过程对晶胞进行优化, 同时采用BFGS算法对内坐标进行弛豫[31]. 收敛标准: 原子间最大作用力为0.01 eV/nm, 最大应力为0.05 GPa, 原子最大位移为5×10-4nm.

Fig.1 Crystal structures of tetragonal(A), monoclinic(B) and orthorhombic(C) Ge3N4 phasesThe small and big balls represent the N and Ge atoms, respectively.

采用准谐近似(QHA)[32,33]进行热力学性质研究. 体系的非平衡态吉布斯自由能G*(V,P,T)可以表示为

(1)

式中:E(V)为总能量;PV为压力项;Fres为电子热运动和磁性对自由能的贡献[32];Fvib为有限温度时晶体中原子振动对自由能的贡献,Fvib可以表示为

(2)

式中:kB为玻尔兹曼常数;nel为价电子数;ωj为谐振频率;n为原子数.

体系的定容热容Cv, 体模量B, 体积热膨胀系数α(V)和格林爱森参数γ可以采用下式计算:

(3)

(4)

式中:V为原胞体积,P为压强,θD为德拜温度,D(θD/T)为德拜积分.

2 结果与讨论

图2给出了3种氮化锗材料在0 ℃时总能量与体积的对应关系. 曲线的最低点对应该体系最稳定结构的体积和总能量. 表1列出了采用GGA-PBE泛函对Ge3N44种结构进行优化后的点阵常数和弹性常数. 由于未找到t-Ge3N4,m-Ge3N4和o-Ge3N4的晶胞常数和弹性常数的相关数据, 本文计算了c-Ge3N4的晶胞常数并与实验值进行对比. 从表1可以看到,c相的点阵常数与相关实验值[12]和理论值[16,20,25]一致, 最大误差仅为1.1%. 计算得到的c相的弹性常数与文献[34]的结果(C11=395 GPa,C12=166 GPa,C44=235 GPa)符合得很好.

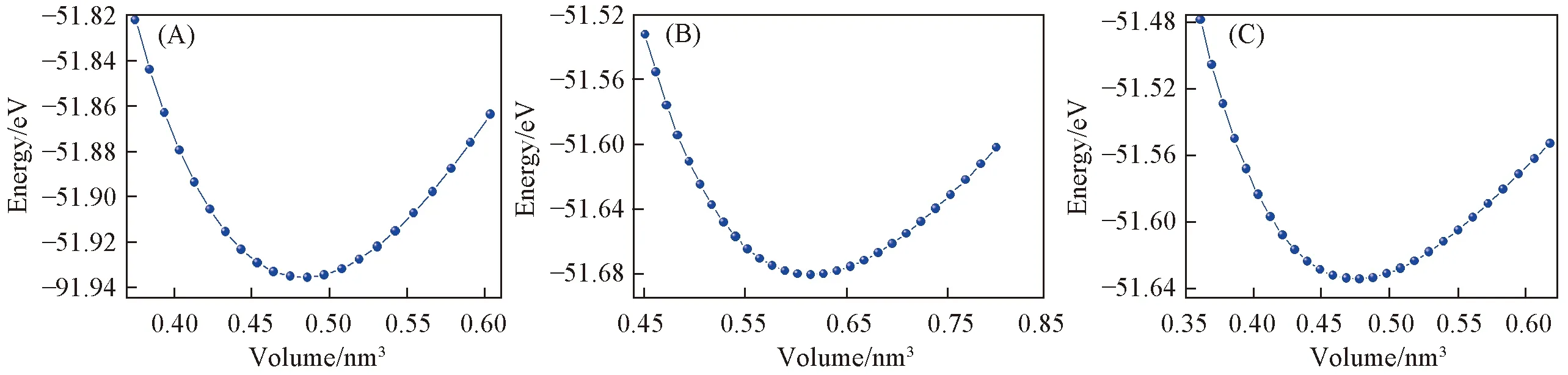
Fig.2 Total energy as a function of volume for t-Ge3N4(A), m-Ge3N4(B) and o-Ge3N4(C)

表1给出的正交相的体模量(203.4 GPa)与c相的体模量(221.8～296 GPa)很接近, 说明o-Ge3N4也属于超硬材料, 其硬度远大于t相和m相. 在3种新结构中,o-Ge3N4的剪切模量最高, 抗剪切应变能力最强. 依据Born弹性稳定性准则, 四方、 单斜和正交晶系的弹性常数应分别满足下列各式[35]:

Table 1 Lattice constants a, b, c (nm), formation enthalpy ΔH (eV), bulk modulus B, shear modulus G and elastic constants Cij(GPa) of Ge3N4

(C11-P)>0, (C33-P)>0, (C44-P)>0,

(C11-C12-2P)>0, (C11+C33-2C13-4P)>0,

(2C11+2C12+C33+4C13+3P)>0, (C66-P)>0 (5)

(C11-P)>0, (C22-P)>0, (C33-P)>0, (C44-P)>0,

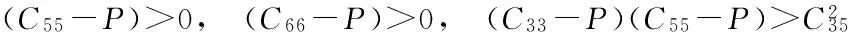
(C11+C22+C33+2C12+2C13+2C23+3P)>0,

(C11-P)>0, (C22-P)>0, (C33-P)>0, (C44-P)>0,

(C55-P)>0, (C66-P)>0, (C11+C22-2C12-4P)>0,

(C11+C33-2C13-4P)>0, (C22+C33-2C23-4P)>0,

(C11+C22+C33+2C12+2C13+2C23+3P)>0 (7)

从表1可见, 在0和20 GPa时,t-,m-和o-Ge3N4的弹性常数分别满足式(5),(6)和(7), 说明三相都能保持结构稳定.c相的计算结果与实验结果一致. 虽然未找到t-Ge3N4,m-Ge3N4和o-Ge3N4的晶胞常数和弹性常数的实验数据和理论结果, 但本课题组之前的工作表明,β-和γ-M3N4(M=Si, Ge)的晶胞常数和弹性常数[24,37]计算值与实验值符合得相当好. 这也能够部分说明本文结果的准确性.

依据几何优化和内坐标弛豫后的晶胞参数, 本文计算了声子色散曲线和声子态密度(PDOS), 结果如图3所示. 声子谱没有虚频, 负频率区域的PDOS为零, 说明3种体系都处在各自的能量最低状态, 在晶格动力学上是稳定的. 研究20 GPa时3种相的声子谱, 未发现虚频. 因为20和0 GPa时的声子谱很相似, 所以在本文未给出. 表1列出的3种相的形成焓都为负值, 弹性常数满足Born稳定性准则, 因此认为t-Ge3N4,m-Ge3N4和o-Ge3N4在0和20 GPa时为结构稳定相态. 从图3(A)可以看到,t-Ge3N4的原胞中含有7个原子, 因此四方相的声子谱包含21支格波(3支声学支和18支光学支). 有3支振动波的谐振频率在Г点(即:G点)趋于零, 这3支即为声学支. 晶格振动主要集中在0～497 cm-1和604～801 cm-1范围内.t-Ge3N4在497～604 cm-1处出现了一个声子禁带. 由分原子声子态密度可知, 低频区主要是来自Ge原子的贡献; 高频区(18 THz或者说604 cm-1以上)主要是来自N原子的贡献; 在中频区(367～604 cm-1) 氮的贡献略大于锗.

Fig.3 Phonon dispersions and phonon density of states for t-Ge3N4(A), m-Ge3N4(B) and o-Ge3N4(C) The blue and red lines are the DOS of N and Ge, respectively.

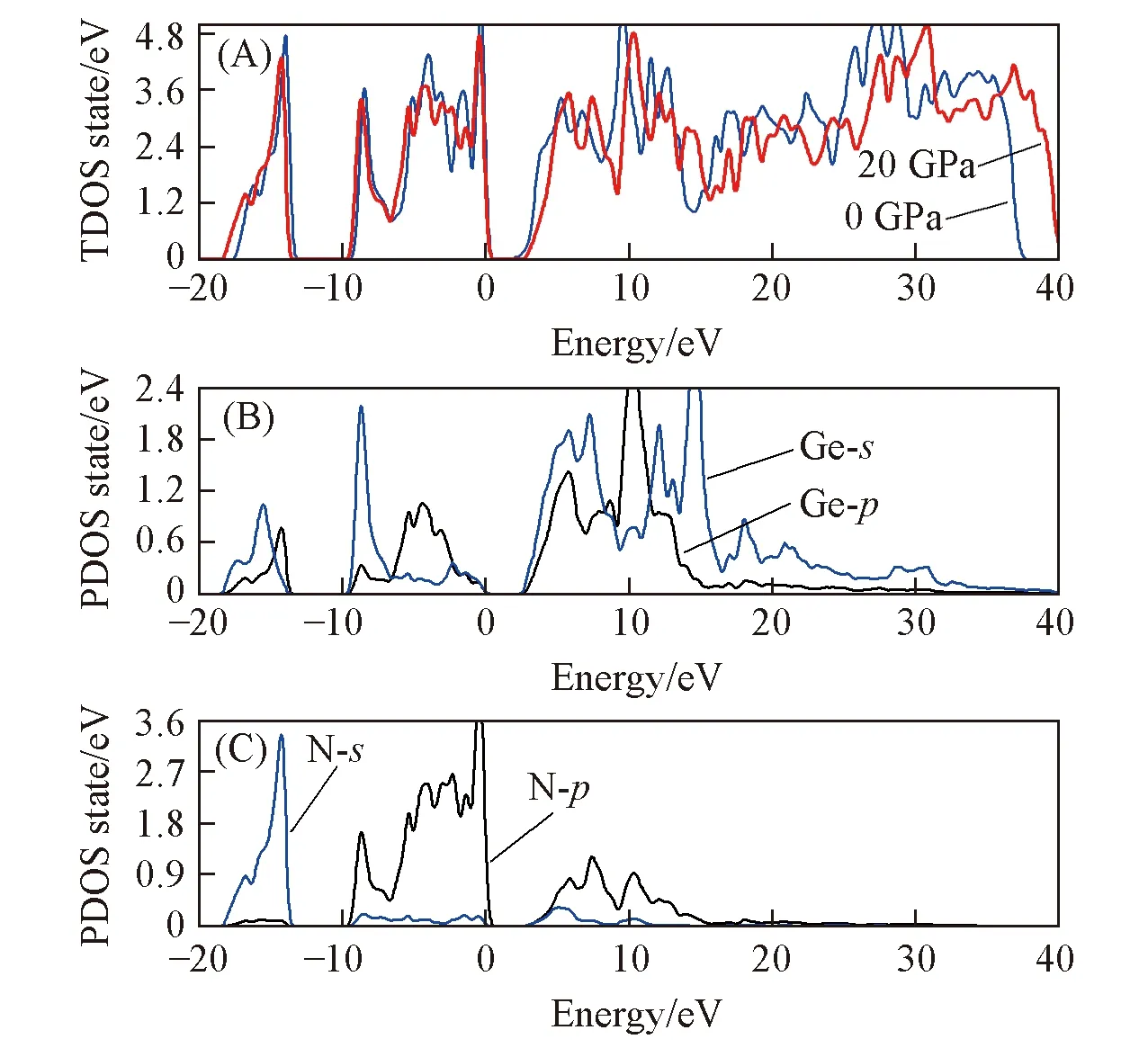
Fig.4 Total(A) and partial density of states for Ge(B), N(C) atoms of t-Ge3N4

如图3(B)所示,m-Ge3N4的声子谱同样是由3支声学支和18支光学支构成的. 光学支在767～834 cm-1处出现了一个宽度为67 cm-1的声子禁带. 分波态密度(PDOS)显示Ge原子和N原子分别占据0～367 cm-1和367 cm-1以上的区域. 因为正交结构Ge3N4的原胞含有28个原子, 所以声子谱的振动波数量较多, 如图3(C)所示. 因为o-Ge3N4和m-Ge3N4的声子态密度很相似, 所以本文并未给出o-Ge3N4的分原子声子态密度, 而是直接给出了总声子态密度. 从图3可知, 3种相的声学支在Г点附近都呈线性变化. 因为Ge的原子量远大于N的原子量, 所以声学支主要是由重原子Ge贡献的, N原子的贡献很小.

Fig.5 Total(A) and partial density of states for Ge(B), N(C) atoms of m-Ge3N4

Fig.6 Total(A) and partial density of states for Ge(B), N(C) atoms of o-Ge3N4

图4～图6给出了Ge3N4的总态密度和各原子的分波态密度, 其中费米能级EF设为零. 从图4(A)、 图5(A)和图6(A)中可以看到, 3种相在20 GPa压强下的总态密度都比0 GPa时的峰值低. 价带态密度向低能区拓展, 导带态密度向高能区拓展, 说明压强增大诱发了离域电子, 使得体系中的电子更加非局域化. 在20 GPa压强下o-Ge3N4的价带分别比m-Ge3N4和t-Ge3N4的价带宽0.8和1.0 eV. 费米能级附近的态密度非常陡峭, 表明有大量电子聚集在这个区域[19]. 3种相的价带都可以分成第一价带(-19～-13 eV)和第二价带(-10～0 eV)两部分. 第一价带主要是N-2s和Ge-4s, 4p轨道贡献的, 第二价带和导带主要由N-2p和Ge-4s, 4p轨道构成[9,12,19]. Ge原子和N原子之间的轨道杂化使得氮化锗体系存在强烈的共价键. 如图4(B, C), 图5(B, C)和图6(B, C)所示, 晶胞内部原子的Wyckoff位置不同导致3种相的态密度存在细微的差别. 零压下t-Ge3N4,m-Ge3N4和o-Ge3N4的能隙宽度分别为1.08, 1.07和1.04 eV. 因为GGA通常低估带隙, 再考虑到态密度是经过展宽的, 所以3种相真实带隙应当更宽. 另外, 计算得到的t-Ge3N4,m-Ge3N4和o-Ge3N4费米能级处的态密度n(EF)分别为2.74, 1.18和6.38, 对应的电子比热系数γe(γe= π2(kB)2n(EF)/3[38])分别为6.46, 2.79和15.03 mJ·K2·mol-1·Cell-1.

Fig.7 Temperature dependences of the normalized bulk moduli B/B0(A) and pressuredependences of the bulk moduli B(B) for the new Ge3N4 phases a. t-Ge3N4; b. m-Ge3N4; c. o-Ge3N4.

图7(A)给出了归一化体模量B/B0与温度的关系, 其中B0是零温零压时的体模量(计算得到t-Ge3N4,m-Ge3N4和o-Ge3N4的B0分别为190.1, 126.2和195.2 GPa). 可以清楚地看到, 本文使用QHA模型结合赝势平面波方法得到的0和20 GPa时的体模量(见表1)符合得很好.B/B0在T<100 K时基本保持不变. 在100～300 K温度区间内B/B0的数值逐渐降低, 曲线的斜率不断增大. 当温度继续升高时,B/B0进入线性下降的区域.o-Ge3N4的B/B0下降最缓慢, 说明在高温时该相仍能保持自身的硬度, 难以被压缩. 如图7(B)所示,B随着压强的升高而线性增大, 体模量对温度和压强都非常敏感. 这是因为体模量是通过体积对压强求导获得的, 温度和压强改变了晶胞体积, 从而改变了体模量.m-Ge3N4的体模量随着温度升高下降的最快, 随着压强升高增大也最快. 3种相的体模量与压强的线性关系表明, 在0～20 GPa范围内没有相变发生.

体积热膨胀系数α(V)主要描述温度改变时材料体积的变化规律, 是衡量材料热力学性质的重要参数之一. 图8(A)为α(V)随温度的变化示意图. 在0～300 K区间内α(V)呈指数增长, 温度高于300 K后α(V) 的增大趋势放缓.t-Ge3N4和m-Ge3N4的α(V)-T曲线非常陡峭;o-Ge3N4的曲线相对平缓, 说明正交相的热膨胀现象较弱. 图8(B)给出了熵S随着温度的变化关系. 可以看到,S在T<200 K时增大得很快; 当温度高于400 K后表现为线性增加.m-Ge3N4的熵增大得最快. 高温下温度T对S和α(V)的影响远小于低温下T对S和α(V)的影响. 如图8(C)所示, 定容热容Cv与T3成正比, 超过300 K之后Cv的增速放缓. 当T>600 K时热容逐渐接近固定值174.6 J·mol-1·K-1(Dulong-Petit极限, 对单个原子为3R,R为摩尔气体常数)[39]. 研究发现Cv的大小满足: 单斜相>四方相>正交相. 图8(D)给出的Cv随着压强的升高而下降, 说明压强和温度对热容的影响截然相反. 当温度固定时m-Ge3N4的α(V),S和Cv最高,o-Ge3N4的α(V),S和Cv参量最低. 这主要是因为o-Ge3N4的硬度最高, 晶胞也是3种相中最致密的.

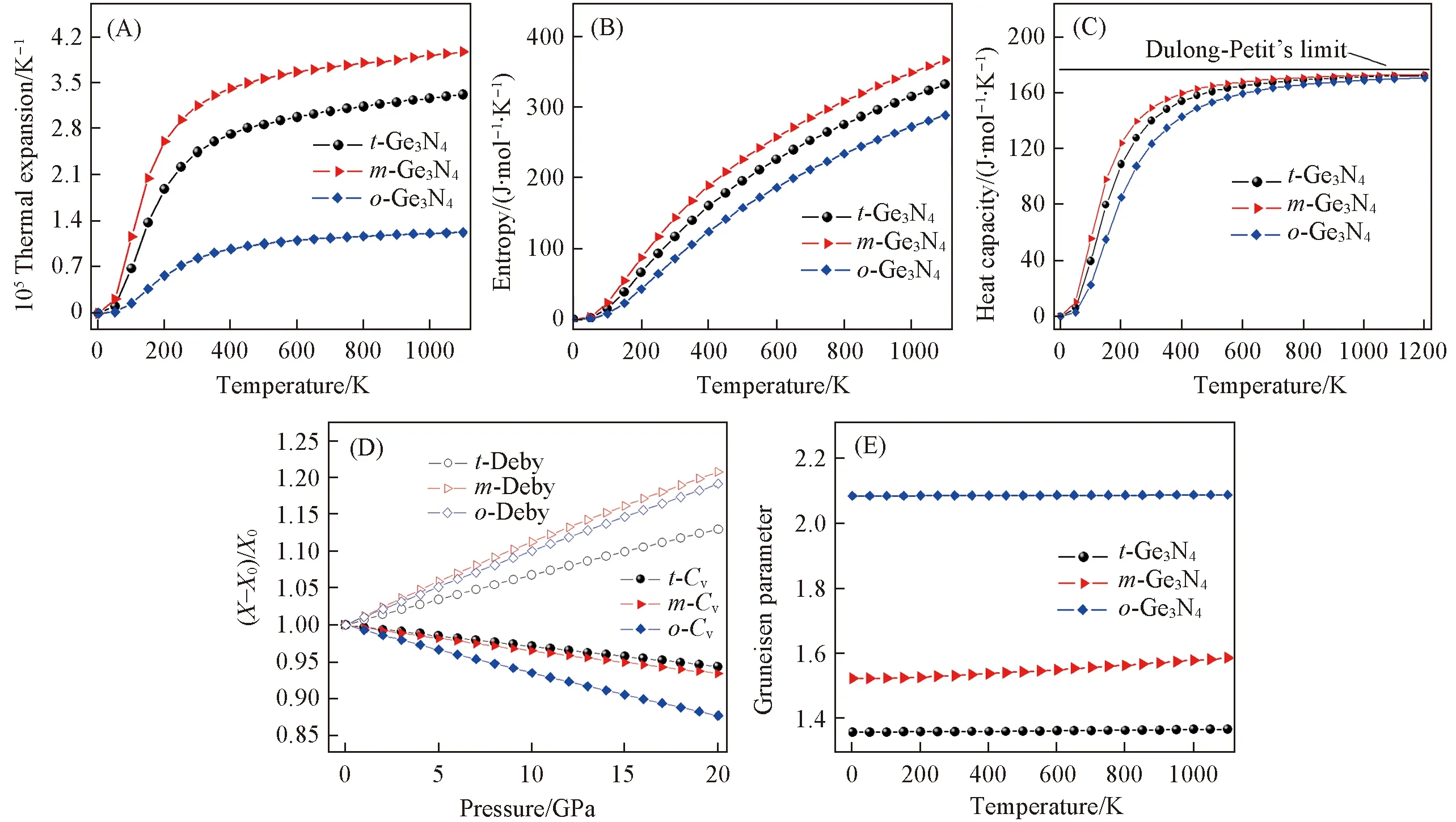
Fig.8 Variations of the volume thermal expansion α(V)(A), entropy S(B), heat capacity Cv(C), normalized Debye temperature θD and heat capacity Cv (D) and Grüneisen parameter γ(E) for the three Ge3N4 compounds

计算得到的德拜温度θD在图8(D)中给出.t-Ge3N4,m-Ge3N4和o-Ge3N4的θD在0～20 GPa范围内分别增加了13%, 21%和19%. 单斜相的θD变化最快, 四方相的θD增速最慢. 德拜温度和体模量的变化规律一致[见图7(B)], 原因是体模量较高的材料通常也具有较高的德拜温度. Grüneisen参数γ主要描述晶胞体积随着温度的改变而变化时晶格谐振频率的变化情况. 如图8(E)所示, 单斜相的γ从0 K时的1.54缓慢增大到1100 K时的1.59. 四方和正交相的γ基本不变(分别为1.36和2.09), 说明t-Ge3N4和o-Ge3N4的晶格谐振频率基本不随温度的变化而变化. 计算得到的0 GPa和300 K时四方(单斜/正交)氮化锗的α(V),Cv,S和θD分别为2.45 [(3.15/0.84)×10-5K-1], 140.1(149.3/123.6 J·mol-1·K-1), 117.6(143.9/85.9 J·mol-1·K-1)和645.5(538.8/820.9 K).

3 结 论

通过量子化学从头算方法结合准谐近似研究了四方、 单斜和正交结构氮化锗的晶胞结构、 电子结构、 声子谱和热力学性质. 考虑到德拜温度、 热容和体模量与压强的线性关系, 再结合3种相在0和20 GPa时的形成焓为负值、 弹性常数满足Born稳定性准则和声子谱无虚频, 本文结果表明, 在0～20 GPa范围内t-Ge3N4,m-Ge3N4和o-Ge3N4都能保持结构稳定. 声子谱的低频区和高频区分别来自Ge原子和N原子的贡献. 能隙宽度分别为1.08, 1.07和1.04 eV, 说明t-Ge3N4,m-Ge3N4和o-Ge3N4都属于半导体材料. 锗和氮之间存在明显的s-p杂化现象. 低温时的体模量B几乎不变, 高温时B的下降速率加快. 这种变化主要是由晶胞体积改变引起的.o-Ge3N4在高温时仍能保持自身的硬度.m-Ge3N4和t-Ge3N4的热膨胀系数分别为o-Ge3N4的3倍和2倍. 热容随着温度的升高而迅速增大, 逐渐趋近Dulong-Petit极限;t-Ge3N4和o-Ge3N4的晶格谐振频率对温度变化不敏感. 非谐效应导致Cv,S和α(V)与温度的关系都不是线性的. 本文计算结果有助于理解氮化锗3种新结构在高温和高压下的性质, 但是此结果还需实验验证.

[1] Lu X., La P., Guo X., Wei Y., Nan X., He L.,J.Phys.Chem.Lett., 2013, 4(11), 1878—1881

[2] Fu R. B., Yang L. Q., Feng L. Y., Guo W.,Chem.J.ChineseUniversities, 2014, 35(4), 825—830(付融冰, 杨兰琴, 冯雷雨, 郭伟. 高等学校化学学报, 2014, 35(4), 825—830)

[3] Hart J. N., Allan N. L., Claeyssens F.,Phys.Rev.B, 2011, 84(24), 245209

[4] Yang H. M., Xu B., Guo X. F., Wen Z. X., Fan X. H., Tian B.,Chem.J.ChineseUniversities, 2013, 34(4), 970—974(杨红梅, 许斌, 郭晓斐, 温振兴, 范小红, 田彬. 高等学校化学学报, 2013, 34(4), 970—974)

[5] Salamat A., Hector A. L., Kroll P., McMillan P. F.,Coordin.Chem.Rev., 2013, 257(13/14), 2063—2072

[6] Ding Y. C., Chen M., Wu W. J.,J.Theor.Comput.Chem., 2015, 14(4), 1550024

[7] Boyko T. D., Hunt A., Zerr A., Moewes A.,Phys.Rev.Lett., 2013, 111(9), 097402

[8] Deb S. K., Dong J., Hubert H., McMillan P. F., Sankey O. F.,SolidStateCommun., 2000, 114(3), 137—142

[9] Duan Y. H., Zhang K. M., Xie X. D.,ActaPhys.Sinica, 1996, 45(3), 512—517(段玉华, 张开明, 谢希德. 物理学报, 1996, 45(3), 512—517)

[10] Serghiou G., Miehe G., Tschauner O., Zerr A., Boehler R.,J.Chem.Phys., 1999, 111(10), 4659—4662

[11] Leinenweber K., O’Keeffe M., Somayazulu M. S., Hubert H., McMillan P. F., Wolf G. H.,Chem.Eur.J., 1999, 5(10), 3076—3078

[12] Yang M., Wang S. J., Feng Y. P., Peng G. W., Sun Y. Y.,J.Appl.Phys., 2007, 102(1), 013507

[13] Chu L. H., Kozhevnikov A., Schulthess T. C., Cheng H. P.,J.Chem.Phys., 2014, 141(4), 044709

[14] He H. L., Sekine T., Kobayashi T., Kimoto K.,J.Appl.Phys., 2001, 90(9), 4403—4406

[15] Wang Z., Zhao Y., Schiferl D., Qian J., Downs R. T., Mao H. K., Sekine T.,J.Phys.Chem.B, 2013, 107(51), 14151—14153

[16] Dong J. J., Sankey O. F., Deb S. K., Wolf G., McMillan P. F.,Phys.Rev.B, 2000, 61(18), 11979—11992

[17] Gao S. P., Cai G. H., Xu Y.,Comput.Mater.Sci., 2013, 67, 292—295

[18] Lü T. Y., Zheng J. C.,Chem.Phys.Lett., 2010, 501(1—3), 47—53

[19] Wang H., Chen Y., Kaneta Y., Iwata S.,J.Phys.:Condens.Matter., 2006, 18(47), 10663—10676

[20] Ching W. Y., Mo S. D., Ouyang L. Z.,Phys.Rev.B, 2001, 63(24), 245110

[21] Horvath-Bordon E., Riedel R., Zerr A., McMillan P. F., Auffermann G., Prots Y., Bronger W., Kniep R., Kroll P.,Chem.Soc.Rev., 2006, 35(10), 987—1014

[22] Soignard E., McMillan P. F., Hejny C., Leinenweber K.,J.SolidStateChem., 2004, 177(1), 299—311

[23] McMillan P. F., Deb S. K., Dong J. J.,J.RamanSpectrosc., 2003, 34(7/8), 567—577

[24] Luo Y., Cang Y., Chen D.,Comput.Condens.Matter., 2014, 1, 1—7

[25] Lowther J. E.,Phys.Rev.B, 2000, 62(1), 5—8

[26] Cui L., Hu M., Wang Q., Xu B., Yu D., Liu Z., He J.,J.SolidStateChem., 2015, 228, 20—26

[27] Kohn W., Sham L. J.,Phys.Rev., 1965, 140(4A), A1133—A1138

[28] Perdew J. P., Burke K., Ernzerhof M.,Phys.Rev.Lett., 1996, 77(18), 3865—3868

[29] Monkhorst H. J., Pack J. D.,Phys.Rev.B, 1976, 13(12), 5188—5192

[30] Ackland G. J., Warren M. C., Clark S. J.,J.Phys.:Condens.Matter., 1997, 9(37), 7861—7872

[31] Shanno D. F., Kettler P. C.,Math.Comput., 1970, 24(1—3), 657—664

[32] Otero-de-la-Roza A., Luańa V.,Comput.Phys.Commun., 2011, 182(8), 1708—1720

[33] Otero-de-la-Roza A., Abbasi-Pérez D., Luańa V.,Comput.Phys.Commun., 2011, 182(10), 2232—2248

[34] Dong J. J., Deslippe J., Sankey O. F., Soignard E., McMillan P. F.,Phys.Rev.B, 2003, 67(9), 094104

[35] Liu Q. J., Ran Z., Liu F. S., Liu Z. T.,J.AlloysCompd., 2015, 631, 192—201

[36] Soignard E., Somayazulu M., Dong J. J., Sankey O. F., McMillan P. F.,J.Phys.:Condens.Matter., 2001, 13(4), 557—563

[37] Yu B. H., Chen D.,Chin.Phys.B, 2012, 61(19), 197102

[38] Zhao Z. F., Li Y. F., Yao N.,Chem.J.ChineseUniversities, 2015, 36(8), 1648—1654(赵昨非, 李元丰, 姚宁. 高等学校化学学报, 2015, 36(8), 1648—1654)

[39] Petit A. T., Dulong P. L.,Ann.Chim.Phys., 1819, 10, 395—413

(Ed.: Y, Z)

† Supported by the National Natural Science Foundation of China(Nos.61475132, 11304141, 11475143, 61501392) and the National Training Programs of Innovation and Entrepreneurship for Undergraduates, China(No.201510477001).

Theoretical Studies on Tetragonal, Monoclinic and Orthorhombic Distortions of Germanium Nitride Polymorphs†

CANG Yuping, CHEN Dong*, YANG Fan, YANG Huiming

(CollegeofPhysicsandElectronicEngineering,XinyangNormalUniversity,Xinyang464000,China)

Applying theabinitiopseudo-potential technique, we had predicted the lattice structures, density of states, phonon dispersion curves of the recently-discovered tetragonal, monoclinic and orthorhombic phases of Ge3N4. The negative formation enthalpy, the satisfactory of Born’s stability criteria and no imaginary frequency can be seen in the phonon dispersion curves proof that the three Ge3N4polymorphs can retain their stabilities in the pressure range of 0―20 GPa. The temperature affects the cell volume, thereby decreasing the bulk modulus. The band gaps show that Ge3N4are semiconductors, while obviouss-phybridizations can be seen in the density of states. The band gaps decrease with applied pressure, which is due mainly to the generation of non-local electrons. Then, the quasi-harmonic approximation is used to study the thermodynamic properties of Ge3N4. The results show that the thermal expansion coefficient, entropy, heat capacity, Debye temperature and Grüneisen parameter are significantly affected by both temperature and pressure. The thermal expansions ofm-Ge3N4andt-Ge3N4are three and two times greater than that ofo-Ge3N4, respectively. The lattice vibration frequency ofo-Ge3N4keeps unchanged at different temperatures. Our results are concordant with the experimental data and the previous results. Therefore, the present results indicate that the combination ofabinitiocalculations and quasi-harmonic approximation is an efficient method to simulate the high-temperature behaviors of different Ge3N4polymorphs. Generally speaking, the results listed in this work are all predictions, which need to be verified by experiments in the near future.

Abinitio; Germanium nitride; Electronic structure; Stability

10.7503/cjcu20150921

2015-11-29.

日期: 2016-03-17.

国家自然科学基金(批准号: 61475132, 11304141, 11475143和61501392)和国家级大学生创新创业训练计划项目(批准号: 201510477001)资助.

O641

A

联系人简介: 陈 东, 男, 副教授, 主要从事量子化学计算研究. E-mail: chchendong2010@163.com