高考选择题的解法*

●张春杰

(学军中学 浙江杭州 310012)



高考选择题的解法*

●张春杰

(学军中学 浙江杭州 310012)

主要针对浙江省高考数学选择题的特点和命题趋势，结合多年选择题的备考思路，分析了一些常见的解题策略和方法:直接法、特例法、排除法和图像法等，力图体现数学本质，提炼数学思想.

高考；选择题;解法

1 知识内容

1)高考数学选择题主要考查基础知识与基本方法，力求知识的覆盖、方法的融合.解决选择题，一般不宜采取长篇大论的思维策略，主要目标是准确和快速.

2)选择题的特点是不需要过程，只需给出选项答案，因此选择题的解法千姿百态、不拘一格.常见选择题的解法有直接法、特例法、排除法、图像法、逆推法、分类讨论法等.

2 命题分析

从历年浙江省数学高考试题来看，试卷的题型结构一直在变化，其中选择题从2015年开始调整为8道，预计2016年保持稳定，仍主要考查数学基本概念，以思维分析判断为主、计算为辅.

3 典题剖析

3.1 直接法

直接法，就是“由因到果”解决问题的思路方法.具体地说，就是由已知条件或相关定理，按照严谨的思路，一步一步直接解决问题的思路和方法.

( )

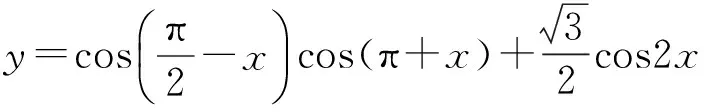
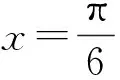
分析 因为

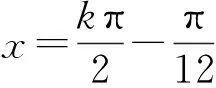
当k=2时，选项D符合.

例2 如图1，已知△ABC，D是AB的中点，沿直线CD将△ACD折成△A′CD，所成二面角A′-CD-B的平面角为α，则

( )

A.∠A′DB≤αB.∠A′DB≥α

C.∠A′CB≤αD.∠A′CB≥α

图1 图2

分析 如图2，作AO⊥DC，由旋转的过程可知，二面角A′-CD-B的平面角为∠A′OE,AO=A′O,从而

同理可得

因为∠A′OA是直线AA′与平面A′DC所成的角(是直线与平面所成角中最小的角)，所以∠AA′D≥∠AA′O,从而∠A′OA≤∠A′DA,于是∠A′DB≥α.故选B.

点评 直接法是解答选择题最常用的基本方法．应用直接法需要有效地整合题目给出的条件，选择一个适当的切入口，进行严谨地论证或说明.直接法的思路有时不宜发现，需要对题目进行仔细分析.

2 特例法

特例法是一种在客观题中经常采用的思维方法.主要特点就是分析题目的条件，从一般情形中找出最有代表性的例子.特例法的特点是过程虽不严谨，但是可以快速有效地解决问题，是一种“小题小做”的典型方法.

例3 一个二面角的2个半平面分别垂直于另一个二面角的2个半平面，则这2个二面角

( )

A.相等 B.互补

C.相等或互补 D.关系不确定

分析 考虑特殊情形，也就是说二面角是180°的情形，另外一个平面只要保证棱与已知平面垂直，可以得出2个二面角没有任何关系.故选D.

例4 函数f(x)=Msin(ωx+φ)(其中ω>0)在区间[a，b]上是增函数，且f(a)=-M，f(b)=M，则函数g(x)=Mcos(ωx+φ)在[a，b]上

( )

A．是增函数 B．是减函数

C．可以取得最大值M

D．可以取得最小值-M

点评 特例法的特点在于选择的例子要典型，具有一般性的特征.特例法不仅可以快速有效地解决选择题，而且在其他类型的题目中可以帮助我们有效理解题意.

3 排除法

排除法其实和特例法是密切相关的.需要针对题目给出的条件进行分析，逐步排除一些明显不符合题意的情况，缩小选择的范围，直至选出正确的选项.

例5 若a,b∈R，则使|a|+|b|>1成立的一个充分不必要条件是

( )

C.a≥1 D.b<-1

分析 对于选项A,取a=b=0.5,则不是充分条件.同理可说明选项B也不成立.对于选项C来说，只需取a=1,b=0,即可说明选项C是错误的.故选D

例6 存在函数f(x)满足：对任意x∈R都有

( )

A.f(sin2x)=sinxB.f(sin2x)=x2+x

C.f(x2+1)=|x+1| D.f(x2+2x)=|x+1|

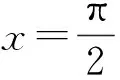
点评 排除法的特点是“逐步筛选”，直至得出正确答案．

4 图像法

图像法，有时也称数形结合法,是充分地把“数”和“形”结合起来解决问题的方法.形是具体的，数是抽象的.利用形寻找解决问题的突破口，打开解决问题的钥匙，再利用数进行严谨地表述.

( )

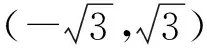
C.(-1,1) D.(-2,2)

分析 不妨令t=3x,由f(x)=0,可知

a=PA-PB∈(-1,1).

故选C.

图3 图4

( )

分析 如图4，由题意可知，点O，A，C，B共圆.当OC为该圆的直径时，|c|取得最大，此时

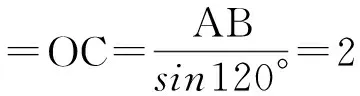
点评 图像法的关键点在于形的把握.所谓形散而神不散，就是要从题目繁杂的条件中准确地画出图形，然后从图形中寻找解决问题的“突破口”.图像法在高考选择题中用途非常广泛.

4 精题集萃

1.已知i是虚数单位，a,b∈R,则“a=b=1”是“(a+bi)2=2i”的

( )

A.充分不必要条件 B.必要不充分条件

C.充分必要条件

D.既不充分也不必要条件

2．过点(1,3)作直线l，若l经过点(a,0)，(0,b),且a,b∈N*，则可作出的l的条数为

( )

A．1 B．2 C．3 D．多于3

3.已知{an}是等差数列，公差d不为0，前n项和是Sn，若a3，a4，a8成等比数列，则

( )

A.a1d>0,dS4>0 B.a1d<0,dS4<0

C.a1d>0,dS4<0 D.a1d<0,dS3>0

( )

A.直线x=2上 B.直线x=1上

C.直线y=2x上 D.直线y=x上

5.在空间中，过点A作平面π的垂线，垂足为B，记B=fπ(A).设α,β是2个不同的平面，对空间任意一点P，Q1=fβ[fα(P)]，Q2=fα[fβ(P)],恒有PQ1=PQ2，则

( )

A.平面α与平面β垂直

B.平面α与平面β所成的(锐)二面角为45°

C.平面α与平面β平行

D.平面α与平面β所成的(锐)二面角为60°

6.已知圆(x+1)2+y2=4的圆心为C，点P是直线l：mx-y-5m+4=0上的点，若该圆上存在点Q使得∠CPQ=30°，则实数m的取值范围为

( )

A．[-1，1] B．[-2，2]

7.设实数a,b,t满足|a+1|=|sinb|=t,下面哪个叙述是正确的

( )

A.若t确定，则b2唯一确定

B.若t确定，则a2+2a唯一确定

D.若t确定，则a2+a唯一确定

( )

9.已知⊙C的方程为(x-2)2+(y-1)2=5，点B的坐标为(0,2)，设P,Q分别是直线l:x+y+2=0和⊙C上的动点，则|PB|+|PQ|的最小值为

( )

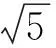
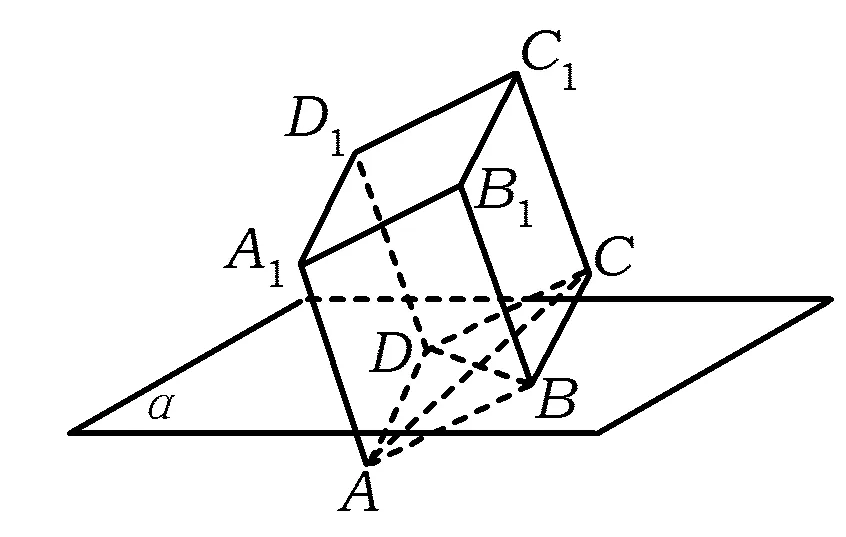
图5

10.如图5,正方体ABCD-A1B1C1D1的棱长为1，底面ABCD的对角线BD在平面α内，则正方体在平面α内的射影构成的图形面积的取值范围是

( )

参 考 答 案

1.A2.B3.B4.A5.A6.D7.B

8.D9.B10.B

�2015-12-16；

2016-01-19.

张春杰(1974-)，男，河南潢川人，中学高级教师，研究方向：数学竞赛.

O12

A

1003-6407(2016)03-46-03