冲刺阶段，试卷讲评要突出解法的选择*

●王永生

(大理第一中学 云南大理 671003)



冲刺阶段，试卷讲评要突出解法的选择*

●王永生

(大理第一中学 云南大理 671003)

高三数学复习过程中, 试卷讲评常伴随始终。结合一次省级测试，就解题突破口的选择，客观题“小题大做”的避免和解题思维障碍的跨越进行了有针对性的讲评尝试。并提出，在冲刺阶段，试卷讲评时，应突出对学生进行解题方法选择的指导，从而有意识地培养学生的数学学习选择能力.

高三数学复习；冲刺阶段；试卷讲评；数学学习选择能力

选择，百度百科解释为“挑选，选取”.在生活中，选择无处不在.在一定阶段，怎样才能做出理性的选择已经成为每个合格公民必须具备的一种基本素养.

经过第一轮的系统复习和第二轮的整体提高后，学生的基本知识、基本方法和基本技能都已初步具备，可实际运用还不够娴熟.冲刺阶段，在众多的模拟考试中，除关注传统的查缺补漏工作外，有一种现象不容忽视.那就是有好多题，2个小时内，学生不是因为不会做，而是因为解法选择不当，不仅导致该题解题失败，还使其他题也没时间求解，从而难以取得较理想的成绩.当教师讲评时或跟同学讨论后才大呼当时没想到实在可惜.

中学生的数学学习选择能力是指中学生在数学学习活动过程中形成和发展起来的，能够对学习对象(客体)进行辨别、筛选的，有助于数学学习的一种个性心理特征[1].

有研究表明，中学生的数学学习选择能力是影响学习成绩的重要因素，二者有着较高的正相关.大部分学生还没有养成良好的解题自我监控的习惯，不能选择合适的解题策略[2].解题中的自我监控是学生数学学习选择能力的一个主要方面.在高三数学复习过程中，冲刺阶段的主要任务是全面提高学生的学习成绩.为此，在试卷讲评时，应突出对学生解题方法选择的指导.

2015年3月，云南省进行了第1次高中毕业生的复习统一检测.由于部分试题解法比较灵活，对学生的选择能力提出了较高要求.借此机会，在进行试卷讲评时，笔者就解法的选择对学生进行了有针对性地指导.

1 利用模式识别，寻找解决问题的突破口

此次考试，选择题得分率最低的是第7题，试题如下：

( )

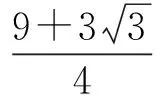
很多学生坦言，此题根本无从下手，考试时只能胡乱猜了一个答案.

一个月前，在复习解三角形内容时已系统讨论过该题的求解.例1只是稍有改变，学生无从下手确实难以理解.可如何选择解题突破口正是学生解题思路选择的一个关键，往往影响着解题的方向，并最终决定了解题的成败.

“当遇到一个新问题时，我们辨认它属于哪一类基本模式，联想起一个已经解决的问题，以此为索引，在记忆贮存中提取出相应的方法来加以解决，这就是模式识别的解题策略.”[3]

基于此，何不利用模式识别，引导学生寻找解决问题的突破口.为此，笔者对例1进行了下面的讲评：

师:当内角C最大时，cosC最小.此题就是在所给条件下求cosC最小时△ABC的面积.那如何求cosC的最小值呢？以前碰到过类似的问题吗？应从哪里入手呢？

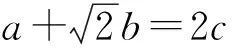
即

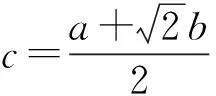
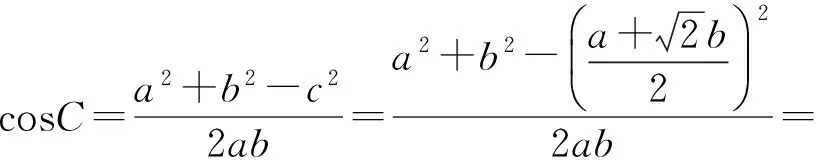
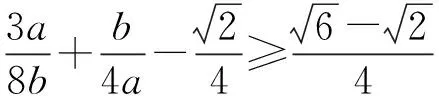
还可由

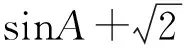
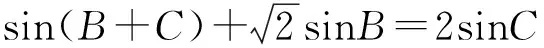
从而

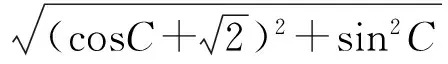
得

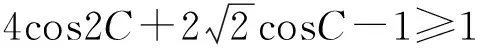
此解法不易想到，由此可见，选择好思考问题的角度往往是解决问题的关键.此题的求解对探求例1的解题思路有何帮助呢？

事实上，在△ABC中,

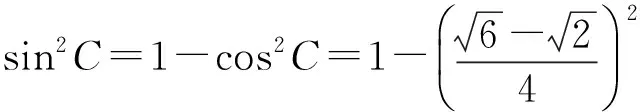
得

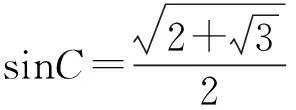
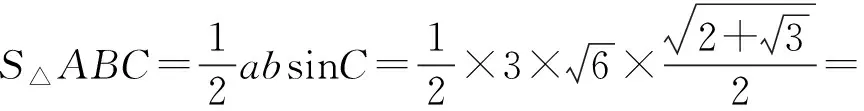
应选A.

在求解过程中，对复合二次根式的化简是例1求解的第2个难点，其关键在于拆项后构造完全平方式，这也是需要大家掌握的基本方法之一.

考试时没办法再求下去，于是只好放弃了.

师:这应该是多数同学最初的想法吧！由于题目多给出了条件b=3，这样思考也无可厚非，但难道就真的没办法求了吗？

事实上，

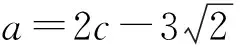
生(众)：好难啊！

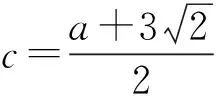
方法相似，但求解确实简化了许多.只是一小点的更改，就可淡化多处的技巧，从而使解法优化.可见，在解题过程中，不同的方法选择，其解题效果明显有所不同.

通过例1的解法分析可知，当碰到一个新问题难以入手时，可尝试通过模式识别寻找解决问题的突破口.对于选择题或填空题，可直接利用模式求解.当然，“模式只是提供了一种相对稳定的样本，既非万能又非一成不变.”[3]于是，在进行模式识别时还应灵活处理，结合题目自身特征，选择更为恰当的解题方案.

2 借助归纳推理，有效避免小题大做

在填空题中，学生出错最多的是第16题，试题如下：

已知递推公式求数列的通项公式一般有2种思考方向.可先由递推公式求出该数列的前若干项，后通过观察、归纳猜想出其通项公式，再进行严格证明；也可通过构造新数列转化为等差、等比数列问题.这正好是“归纳推理”和“演绎推理”的具体体现.

“这种由某类事物的部分对象具有某些特征，推出该类事物的全部对象都具有这些特征的推理，或者由个别事实概括出一般结论的推理，称为归纳推理.”[4]“从一般性的原理出发，推出某个特殊情况下的结论，这种推理称为演绎推理.”[4]

《普通高中新课程标准(实验)》的一大特色是增加了对“推理与证明”的学习.《普通高等学校招生全国统一考试大纲(课程标准实验版)》也提出了“了解合情推理的含义，能利用归纳和类比等进行简单的推理，了解合情推理在数学发现中的作用”的考试要求.

基于此，笔者对例2进行了如下的讲评：

师:由条件可知

即

(an+1an+1)2.

因为an>0,所以

2an+1=an+1an+1,

即

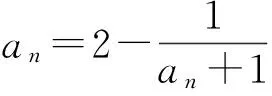
学生：不好求解.

师:先来看人教A版普通高中课程标准实验教科书《数学(选修2-2)》第71页的例题：

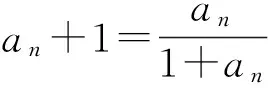
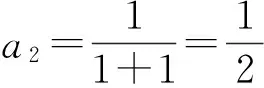
师:非常好，这就是归纳推理.你能尝试着解决上面的问题吗？

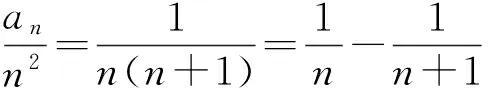
有研究表明，当前高中生数学“归纳推理”能力差异大，主要是受教师教学的影响.并提出，只有在数学教学中有意识地渗透“归纳推理”思想，才能提高学生的“归纳推理”能力.[5]

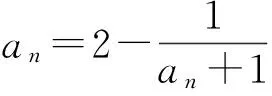
得

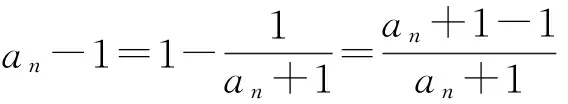
从而

即

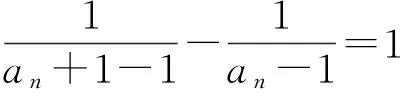
应当说，这样的构造也不算难，多数学生也曾想这样做，可由于思维要求较高，多次尝试也未能如愿.既使勉强走对了路，解决填空题也未免有“小题大做”之嫌.可见，同一道题，考试时选对方法显得多么的重要，而这正是数学学习选择能力的一个重要方面.

3 通过构造函数，成功跨越思维障碍

“从近几年的高考试题看，在函数背景下考查不等式的证明成为了一种新的命题趋势.”[6]而且往往还以高考压轴题的形式出现.平时的模拟考试，学生基本上都难以完成这一道题.这已经成为学生心中难以逾越的一座大山.

此次高考试题理科第21题仍以函数背景下不等式证明的形式出现.

1)求f(x)的单调区间；

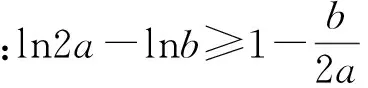
“从心理学角度来看，证明的过程就是把新的命题(论题)与已有认知结构中的有关命题和概念(论据)关联起来，通过对它们的重新组合，综合运用各种推理形式而使新的命题获得意义的过程.”[7]

据此，顺着学生的思路，笔者进行了如下的讲评：

(众生哑然.)

师:其实有一部分同学已经做到了这里，其“思路点”是正确的，可由于其“扩展力”和推理能力不够，最终没能正确完成解答.

事实上，因为a>0，b>0，所以

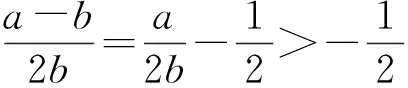
从而

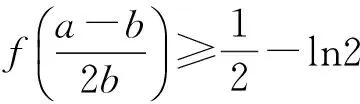
化简得

考试时，常会碰到这样的思维障碍.如何有效跨越呢？一种方式是顺其自然，坚持到底；另一种方式是另寻他途.此问能否另寻他途呢？

g(x)min=g(1)=1，

后略.

师:不错，此法通过构造新的函数，成功跨越了思维的障碍.虽然看上去比参考答案要麻烦一些，可思路清晰，一气呵成，实为此问证明的上佳之策.而这种方法也是函数背景下不等式证明的常用方法.

考试时，有些题目，学生不是不会做，而往往是因为解法选择不当，从而导致未能获得理想的成绩.此次考试，笔者选择了3道相对困难的题目就解题突破口的选择、客观题“小题大做”的避免和解题思维障碍的跨越进行了有针对性的讲评.虽然不能涵盖解法选择的全部，但对学生即将面对的高考却是极有帮助的.冲刺阶段，试卷讲评的方式很多，但突出对学生进行解法选择的指导却显得尤为重要.

[1] 张文宇，范文贵.中学生数学学习选择能力研究[J].长春师范学院学报：自然科学版，2007,26(4)：121-125.

[2] 张文宇，范文贵，张守波.中学生数学学习选择能力与学习成绩相关性研究[J].数学教育学报，2008,17(1)：59-61.

[3] 罗增儒.数学解题学引论[M].西安：陕西师范大学出版社，2001.

[4] 人民教育出版社课程教材研究所，中学数学课程教材研究开发中心.普通高中课程标准实验教科书：数学选修2-2[M].北京：人民教育出版社，2007.

[5] 严运华.高中生数学“归纳推理”能力的微型调查[J].中学数学教学参考：上旬，2012(9)：62-65.

[6] 汪中明，罗新兵.例说函数背景下的不等式证明[J].中学数学教学参考：上旬，2011(11)：53-54.

[7] 朱水根，王延文.中学数学教学导论[M].北京：教育科学出版社，2001.

�2015-10-13；

2015-11-17.

王永生(1974-)，男，云南大理人，中学高级教师，研究方向：数学教育.

O12

A

1003-6407(2016)03-36-05