亲历探究过程 收获别样的美——从一节高三复习课谈起*

●章建斌

(青田中学 浙江青田 323900)



亲历探究过程 收获别样的美
——从一节高三复习课谈起*

●章建斌

(青田中学 浙江青田 323900)

专题复习课要坚持以学生的心理特点和认知规律为抓手，精心创设问题情境，激发学生的学习欲望，让学生充分感受提出问题、探究问题、解决问题的过程，不断完善学生的知识网络体系，有效提升学生的数学思维能力.笔者以一节平面向量专题复习课为例，谈谈在复习课教学设计上的一些思考.

知识网络体系；数学思维；数学能力；三值三线

1 课堂简录

1.1 原题呈现

1.2 学生解题方法呈现

1)(代数法)因为λ=1,所以

图1

2)(代数法1)因为λ+μ=2,所以

λ2+λμ+μ2=λ2-2λ+4=(λ-1)2+3,

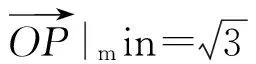
(λ+μ)2-λμ≥

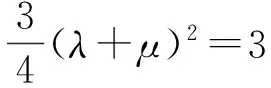
当且仅当λ=μ=1时，等号成立.

(几何法)由λ+μ=2，得

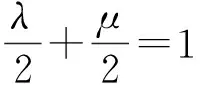
图2

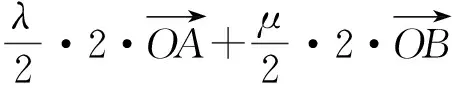
3)(代数法)因为λ=2μ,所以

图3

1.3 问题探究，展示规律

师：很精彩，上述3个小题讲述了：1)λ,μ的3种关系：即λ为定值；λ，μ之和为定值；λ，μ的倍数关系.2)解决平面向量问题主要的方法有代数法和几何法.3)在解决平面向量问题时，涉及到了方程、函数、不等式和平面向量的几何意义.

师(追问)：第1)小题中若λ=λ0，μ∈R,则点P的轨迹是什么？

(教师引导学生自己先画一画，再分组讨论，最后给出点P的轨迹.)

师：第1)小题中若μ=μ0，λ∈R,则点P的轨迹是什么？

图4 图5

师：第2)小题中若λ+μ=t0，则点P的轨迹是什么？

师：第4)小题中若λ=k0μ，则点P的轨迹是什么？

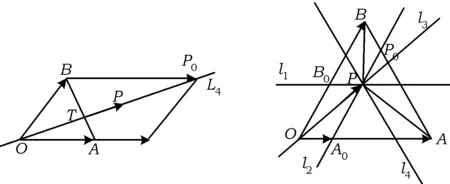
图6 图7

师：大家的思维很活跃.在同学们的努力下，我们发现了非常漂亮的规律(如图7所示).若μ=μ0,λ∈R，则点P的轨迹是直线l1；若λ=λ0,μ∈R，则点P的轨迹是直线l2；若λ=k0μ，则点P的轨迹是直线l3；若λ+μ=t0，则点P的轨迹是直线l4，我们不妨称之为“三值三线”.

1.4 问题拓展，提升能力

师：请同学回答第4)小题的做法.

(学生思考，举手的学生明显少了.)

师：我们请一位还没有完成的同学谈谈他的做法，看看问题出在哪里？

师：其他同学的疑惑是不是也在这里？

生(众)：是.

师：请同学们相互讨论，给出生1接下去的解题思路.

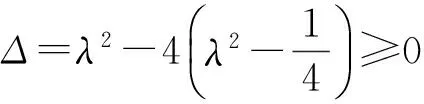
即

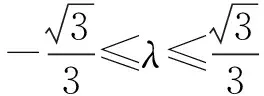
故

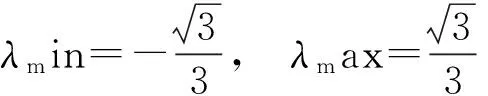
师：很好！生2利用了方程思想，请大家注意方程的形式特征.有没有同学用几何法解决的？

(整个班级静悄悄，过了一会，有学生站起来回答.)

图8

图9

�2015-11-19；

2015-12-23.

章建斌(1979-)，男，浙江青田人，中学一级教师，研究方向：数学教育.

O123.1

A

1003-6407(2016)03-18-03