一个条件等式派生出的若干不等式链*

●何 灯 李云杰

(福清第三中学 福建福清 350315)



一个条件等式派生出的若干不等式链*

●何 灯 李云杰

(福清第三中学 福建福清 350315)

文章以一个条件等式为出发点，建立了2条不等式链，并由此派生出与一些经典不等式竞赛试题相关的若干不等式链.

条件等式；不等式链；数学竞赛

1 问题缘起

文献[1]和文献[2]中研究了以“p,q,r为正实数,且p2+q2+r2+2pqr=1”为条件的一类不等式的证明,得出了若干结论.特别地,文献[2]中归纳了该条件下的5个性质,并应用这些结论证明有关条件不等式.

性质 设p,q,r为正实数,且p2+q2+r2+2pqr=1,则

(1)

(2)

3)p+q+r≥2(pq+qr+rp);

(3)

(4)

(5)

文献[3]则给出了上述5个性质的统一的三角代换法证明.在拜读3篇文章的同时,笔者萌生一个想法：能否将上述零散的5个不等式统一成一体,构成一条不等式链？经探究,得到了2条主要的不等式链,并由此派生出与一些经典不等式试题相关的若干不等式链.

2 2条基础不等式链

结论1 设p,q,r为正实数,且p2+q2+r2+2pqr=1,则

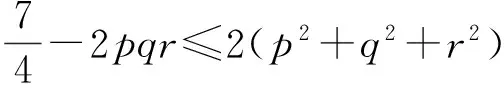
结论2 设p,q,r为正实数,且pq+qr+rp+2pqr=1,则

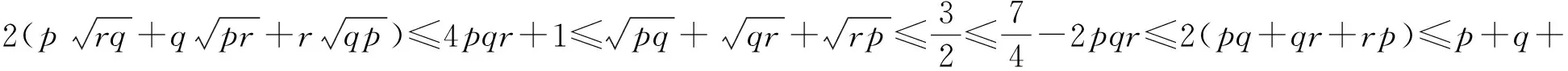
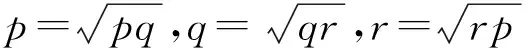
由于上述2个结论可以相互转化,限于篇幅,下面仅针对结论1给出其若干应用.

3 结论1的应用

(第48届中国国家集训队试题)

分析 令u=4p2,v=4q2,w=4r2,则已知条件转化为p2+q2+r2+2pqr=1,待证不等式等价于

例2 设正实数x,y,z满足xy+yz+zx+xyz=4,求证：x+y+z≥xy+yz+zx.

(1996年越南数学奥林匹克竞赛试题)

分析 令xy=4p2,yz=4q2,zx=4r2,则已知条件转化为p2+q2+r2+2pqr=1,待证不等式等价于

例3 设非负实数x,y,z满足x2+y2+z2+xyz=4,求证：xy+yz+zx-xyz≤2.

(第30届美国数学奥林匹克竞赛试题)

分析 令x=2p,y=2q,z=2r,则已知条件转化为p2+q2+r2+2pqr=1,待证不等式等价于

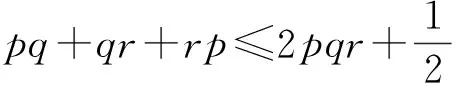
(2005年伊朗数学奥林匹克竞赛试题,2007年美国国家集训队试题)

(2011年中欧数学奥林匹克竞赛试题)

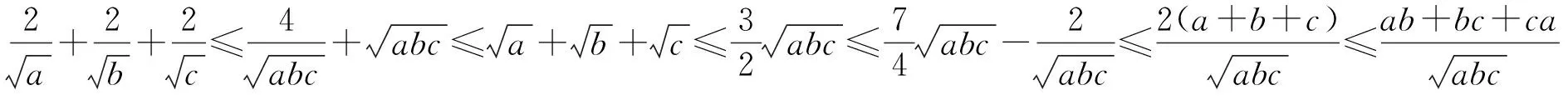
由上观之,通过对文首5个性质的串联,本文所建立的2条基础不等式链能够对一类不等式赛题给出上界、下界或隔离,并由此发现一些相关的不等式.2个结论的更多应用,留给有兴趣的读者继续探究.

[1] 陈建兵,邹守文.一个条件等式派生的不等式在证明竞赛不等式试题中的运用[J].中学数学研究,2011(5):46-49.

[2] 邹守文.一类不等式奥林匹克竞赛试题的共同背景[J].中学教研(数学),2012(9):43-46.

[3] 查正开.一类代数问题的三角解法[J].中学教研(数学),2015(4):15-19.

[4] 李建潮.一类三角形不等式的证法初探[J].河北理科教学研究,2014(4):41-43.

[5] 张俊.一个三角形恒等式繁衍出的代数不等式[J].数学通讯,2010(9):61-62.

�2015-09-08；

2015-12-19.

何 灯(1984-)，男，福建福州人，中学二级教师，研究方向：初等数学、不等式.

O122.3

A

1003-6407(2016)03-31-03