对错题与“错题”的几点思考*

●黄琳婕 方均斌 蒋丰盈

(温州大学数学与信息科学学院 浙江温州 325035)



对错题与“错题”的几点思考*

●黄琳婕 方均斌 蒋丰盈

(温州大学数学与信息科学学院 浙江温州 325035)

错题一词在数学教育中使用颇为频繁，但其含义似乎没有统一.为此，提出错题、错解题、“错题”3个概念，由于当下对错解题的研究颇多，故着重对错题及“错题”的存在及教育价值进行一些探析.认为，错题及“错题”与数学教育永恒伴随，不能回避，故必须正视其教育价值.错题及“错题”的教育价值主要体现在对教师及学生批判意识的教育及自我反思层面上，其研究目前不是很多，具有很大的深入空间.

错题；错解题；“错题”；教育价值

数学教育中的“错题”一词大家并不陌生.然而，这个概念似乎大家并不在意它的辨析.查阅相关文献，发现“错题”有2个含义：一是指内在逻辑有错误的数学问题[1]；二是指解错的数学问题[2].其实，还有一类指存在争议的数学题：“错题”(特意加引号)[3]，它专指不吻合数学习题标准[4]的数学题.本文试图对错题等相关概念及其在数学中的教育价值进行一些梳理，请大家批评指正.

1 错题概念的明确化

错题到底属于“命题者犯错”还是“解题者犯错”，这个概念目前依然没有统一的说法，而且指“解题者犯错”大有约定俗成之势.笔者认为，如果指“解题者犯错”不太科学，因为任何一个正确的数学问题都有可能被解题者解错而“冤枉地”被称为错题，这样，错题就属于“因人而异”的一个名词而“不知所云”.我们应该把“解题者犯错”的正确数学问题称之为“错解题”，而错题应该专指因命题者行为而导致数学问题本身存在逻辑错误(应用题还包括与实际情况不符等现象)的问题.很多中小学教师所研究的错题实质上是指“错解题”.

一些学者为了数学教学的可操作性，对“正确的数学问题”尤其是学生面对的数学习题提出了具体的要求，例如，戴再平先生对数学习题提出了评判的科学性标准[4]：

1)有关的概念必须是被定义的；

2)有关的记号必须是被阐明的；

3)条件必须是充分的、不矛盾的；

4)条件必须是独立的、最少的；

5)叙述必须是清楚的；

6)要求必须是可行的.

然而，随着人们数学教育观念的改变，提出了不吻合戴先生所提条件而致的“错误的数学问题”也存在教育价值的问题[6].因为中小学教材中很多用词(概念)根本没有像高等数学一样进行严格定义，例如“规律”、“未知数”等，这些用词尽管未严格定义，但它们却与基础教育阶段的数学“形影相随”，这类除了文献[4]提出科学性要求的3)中的“条件不矛盾”以及5)中的“叙述必须是清楚的”之外的数学习题(或问题)我们姑且称之为“错题”(特加引号).此类“错题”目前研究的文献不是很多，属于数学教育研究的盲区，甚至有些数学教育者可能把其作为“禁区”而不加理会.我们提出的错题标准不仅涵盖了戴先生指出的违背3)中的“条件不矛盾”以及5)中的“叙述必须是清楚的”要求之外，还包括所提条件与结论存在矛盾等.

2 错题及“错题”的存在及教育价值

尽管我们力图避免数学教育过程中某些“负面”的东西，但是，错题、错解题、“错题”依然与数学教育形影相随，无法避免！既然如此，我们不能采取鸵鸟政策，只能坦然面对.其实，我们很多教师已经发现学生出现频率比较高的错解题(易错题)的研究与教育价值，可以当作一面“镜子”去发现学生的思维和心理盲区，将错解题当作一种很重要的教育资源，一些学生也用自己平时的错解题去进行反省，也达到较好的自我教育目的.由于错解题的教育价值已经引起大家的关注并进行了很多的研究，因此，本文着重就错题和“错题”的存在及教育价值进行一些探析.

2.1 错题的存在及教育价值

错题的负面作用大家都很清楚.例如，在重大考试中，出现错题往往使一些学生在考试中的水平发挥失常，有时甚至出现社会问题.例如，某年某省的数学高考题曾因出现疑似错题就发生了很大的社会风波.出错题固然可悲，但是，学生不敢在考场上提出对考题的质疑，则是因我们长期忽视错题的教育及研究价值所致.

2.1.1 错题是教师职业技能与职业态度的一面镜子

数学教师素有追求严谨的“美称”，如果数学教师出错数学题，很可能是专业素养不够或者注意力不够集中而致，越是重大的考试，教师越需要注意数学问题的科学性.

案例1f(x)是定义在R上的以3为周期的奇函数，且f(2)=0，则方程f(x)=0在区间(0，6)内解的个数的最小值是

( )

A.2 B.3 C.4 D.5.

(2005年福建省数学高考理科试题第12题)

该题一般学生仅推理出：f(1)=-f(1)=f(2)=0，f(4)=f(1)=0，f(5)=f(2)=0，f(3)=f(0)=0(因为f(0)=f(-0)=-f(0)，所以f(0)=0)，很难发现：由-f(1.5)=f(-1.5)=f(-1.5+3)=f(1.5)得到f(1.5)=0，因此f(4.5)=f(1.5)=0，正确答案为7(而选项上没有出现)！

由于该题属于选择题，一般解题者如果能够根据自己的推理找到“答案”往往也就掉以轻心了.针对于隐函数的问题，因为“隐”字当头，不注意挖掘，很可能遗漏或者产生矛盾.

2.1.2 错题是培养学生形成批判意识的一种手段

尽管我们力图回避错题以免“干扰”学生的数学学习，但这样做很可能使学生对错题的“免疫力”降低，一旦遇到错题，往往怀疑是自己的能力而不是这些错题本身.其实，一些学生自己对数学错题的判断能力差也是很懊恼，曾经做过调查，在所调查的中学生和大学生中，分别有71%和62%对教师故意在平时放个别错题以测试他们的判断能力表示理解和支持[5].

案例2 已知函数f(x)满足f(sinx)=cos3x，求f(cosx)的表达式.

将这道题作为例题在师范类学生面前讲解.

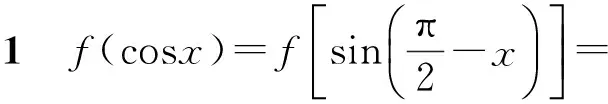
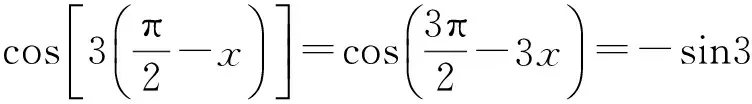
学生们面面相觑，不清楚这2种结果完全相反的解法到底错在哪，几乎没有学生敢于质疑问题本身，而将注意力集中在这2种解法是否有误！师范类学生作为未来的教师，面对铺天盖地的数学习题，没有辨别错题和对问题评价的能力，将很难承担将来的职业需求！

案例3 一次寻找错题的尝试.

这是笔者之一在中学教书时所遇到的案例.有一次单元测试，笔者发现有一道选择题出错了(出现了2个正确选项)，但修改肯定会让学生发现答案，于是就说：“本卷中可能有一道错题，如果你指出来了，就加分，否则不给分.”结果由于教师没有指出是具体哪个类型的数学问题出错，一些学生把自己不会做或者找不到选项的选择题认为是错题.这件事引来了数学组教师的争议.特别是老教师不赞同这样的做法，他们认为：这会对检测学生学习的真正情况产生偏差，应该不做任何提示，只要让学生找到那道错题的2个选项中的一个就可以给分，这样就不影响学生的测试了.其实，从这里我们可窥学生遇到错题出现不知所措或者浑然不知等现象的一些原因，他们的批判性意识应该通过各种手段有意识地进行培养，尽管找错题仅是其中的一种手段.

2.2 “错题”的存在及教育价值

上世纪90年代闹得沸沸扬扬的“船长年龄问题”就属于“数学习题科学标准”之外的数学问题.加州大学教授费尔德出了一道题目：“在一条船上，有75头牛、32只羊，请问船长的年龄有多大?”这道题目让64%的法国孩子和40%的美国孩子得出“船长年龄为43岁”的结论，他们直接用75减去32来算船长的年龄.著名数学教育家张奠宙曾对中国孩子提出同样的问题，却发现有90%的中国孩子得出“船长年龄为43岁”.此类“错题”对学生的测试结果让我们数学教育者有种“五味杂陈”的感觉：说不出味道但又很难受.其实，长期以来，“错题”一直被我们数学教育工作者拒之门外，才造成了这样的调查结果.随着数学教育的逐步深入和视野的扩展，我们不得不正视“错题”的存在及教育价值.

2.2.1 “错题”促使学生反省数学问题的形成过程

以往我们的学生往往只管做题，很少考虑数学问题的来源及实际情况.其实，数学问题来源无非来自2个主要方面：一是来自数学本身；二是来自生活情境.这些问题的产生往往一开始不一定会符合文献[4]提出的“数学习题科学标准”.在问题解决的过程中往往会发现这些数学问题属于“错题”,甚至错题.学生在接触“错题”或者错题时，只要教师合理引导，就会让学生感悟到平时所做的数学题其实有一些是通过“人为加工的”，属于“客观存在”的人为问题.

案例4 列方程组解应用题.

学生通过解一元一次方程，知道可以设立未知数通过方程来解决一些实际问题.然而，教师在教学二元一次方程内容的时候，提出：我今天早上吃2种早餐：蛋糕和牛奶，一共花了7元，请问：蛋糕和牛奶各多少钱？显然这位教师提出的是“错题”，因为这个问题的“条件不是充分的”，当教师补充：“如果买蛋糕的钱比牛奶多1元，你能够知道结论吗？”一些学生通过观察可能马上会得出答案：“牛奶是3元，蛋糕是4元.”教师再说：“如果我再加条件：买蛋糕的钱是牛奶的2倍，而且前面的2个条件不变，你能够知道结论吗？”一些学生感觉自己凭直觉得到的答案好像不满足第3个条件，思考：满足前2个条件是否还存在满足第3个条件的答案？好像不行，但又说不出理由.这样，解二元一次方程组的需要就进入了学生的视野，而且，学生在后续的学习过程中知道，求解2个未知数往往只需设立2个方程即可.

很多数学问题是通过其他数学问题变化而来的，在问题变化的过程中，往往回避不了“错题”和错题的过渡环节.同样，现实问题很复杂，其“毛坯数学问题”往往属于“错题”，甚至是错题.只有对一些信息进行取舍，才能够成为“符合科学性”的数学问题;只有让学生经历过这些过程，才能够体验数学的“再创造”学习.新加坡的数学教育家李秉彝先生在与笔者之一的交流中打了个比喻：“我们不能老是让学生坐在餐厅里品尝‘数学美食’，有时应该让他们去‘数学厨房’看看，这些‘数学美食’是怎么做出来的.这些‘漂亮的数学美食’是如何从那些不那么漂亮甚至有些丑陋的‘原材料’中加工过来的.”

2.2.2 “错题”促使教师研究数学与生活的交融

数学源自生活，从生活中的问题提炼到“符合科学性”的数学问题往往需要经历从“错题”甚至错题的过程.不仅如此，数学应用过程中也需要经历“错题”甚至错题的过程.

案例5 一个学生的尴尬回答.

其实，数学在应用的过程中需要和生活交融，很多问题尽管有数学的成分，按照数学问题来做却与实际相违背，一些问题的处理不一定按照数学的游戏规则进行.此类问题虽与生活交融但仍该列入“错题”甚至是错题范畴.如果添加诸如“小张与小李在平时一起消费的时候都采取AA制”之类的说明，就可以成为一个“正确的数学问题”了！很多具有“实际成分”的“数学问题”，或者具有“数学成分”的“实际问题”，应该用生活及数学的双重眼光审视后才能够成为“正确的数学应用题”.例如，涉及到浓度问题，教师在编拟问题时必须考虑实际溶解度的问题；又如，编拟年龄问题的数学应用题，则不可以出现诸如“爷爷比爸爸大123岁”[3]之类的尴尬现象！

2.2.3 “错题”是数学教学避免纠结的一种过渡

前面我们谈过，基础教育阶段中的很多数学概念是不加定义的，也正因为此，与这些概念相关的数学问题往往都是“错题”，一旦较真，麻烦不断，只能“约定俗成”而“将错就错”，从而避免了一些纠结.

案例6 观察下面一列数,按某种规律在横线上填入适当的数,并说明你的理由.

(2004年浙江省温州市、台州市联合中考试题)

这是一道“错题”，因为按照数学上的理解，一个数列可以写出其通项公式，就认为这个通项公式就是它的“规律”，这个数列的一个通项公式为：

只要控制k的值，第4项可以为任何值.好在编题者已经注意到这个现象，增加了“你的理由是______.”不过如果一位学生在第4项随意填上一个数，然后在后面的理由上写着：“胡思乱想”，不知道改卷的教师该如何评分？

这个案例的问题症结就在于中小学里的“规律”一词是不加任何定义的，只能“约定俗成”也就“相安无事”了！其实，如果按照严格的“科学标准”，基础教育阶段的数学问题中很可能存在大量的“错题”，为此，陈重穆和宋乃庆先生指出了“注重实质，淡化形式”的观点[7]，避免纠结于一些“非本质”的数学问题，也就是说，很多中小学所涉及的数学问题从严格意义上讲都是“错题”，但只要学生理解或者领会所面对的数学问题的数学实质，也就不需要“纠缠”了！可以这样认为，一些“错题”是数学教学避免纠结的一种过渡，也是吻合基础教育阶段基本特征的一种数学问题.

2.3 错题与“错题”教育价值的实现

前面笔者着重谈了错题和“错题”的概念及其存在与教育价值.其实，尽管可能一再回避错题及“错题”，但它们永远与数学教育相伴相随，应该坦然对待，这方面的话题在世界范畴可能也是一个空白，如何实现错题及“错题”的教育功能，这需要大家一起努力.

首先，尽量避免在重大考试中出现错题以免产生社会负面影响，这是理所当然的共识，但要做到这点确实很不容易.教师可以将历年重大考题中出现的错题或者有争议的数学问题进行审视，引以为戒.此外，如果在平时的练习中偶然发现错题，应该不忙于纠正，可以让学生自己寻找错题，以提高学生的批判性意识，这也是一个不错的教育手段，以往这方面的做法不多，建议遇到这种情况可以“借机教育”.至于是否故意出错题让学生寻找，这方面的研究我们期待大家关注并进行一些实践性工作.

其次，应该让一些“错题”进入我们的数学教育研究视野.例如:1)根据数学问题让学生创设生活情境，体验数学与生活之间的“千丝万缕”关系；2)添加或者减少数学条件，使数学问题的解决能够确定或者不矛盾，用这种手段让学生把握正确数学问题形成的实质；3)利用一些“错题”作为数学教育的“花絮”，既提高学生的批判意识，又增加一些数学教学的乐趣.

随着数学教育观念的改变，尤其是开放题的进入，人们对数学问题的要求也越来越“宽容”，哪些“错题”可以融入我们的数学教育，这方面的研究亟待大家的参与.

[1] 黄恒进.一道高考错题引起的思考——谈抽象函数的解题策略[J].试题与研究：教学论坛，2009(4)：42-43.

[2] 洪菲菲.一道错题引发的教学思考[J].内蒙古教育，2015(5)：52-54.

[3] 方均斌.例说“错题”的教育价值[J].数学通报，2006，45(5)：54-56.

[4] 戴再平.数学习题理论[M].杭州：浙江教育出版社，1996：35-65.

[5] 方均斌.数学信息处理的批判性意识的调查与思考[J].数学教育学报，2010,19(1)：48-50.

[6] 楼盘网.小学奇葩数学题闹笑话：爷爷比爸爸大123岁[EB/OL].http://ganzhou.loupan.com/html/news/201511/2064880.html.

[7] 陈重穆，宋乃庆.淡化形式，注重实质——兼论《九年义务教育全日制初级中学数学教学大纲》[J].数学教育学报，1993，2(2)：4-9.

�2015-11-19；

2015-12-15.

黄琳婕(1991-)，女，浙江台州人，硕士研究生，研究方向：数学教育.

O12

A

1003-6407(2016)03-24-04