再探平面向量数量积的应用*
2016-12-01寇恒清
●寇恒清
(上海市黄浦区教育学院 上海 200023)
再探平面向量数量积的应用*
●寇恒清
(上海市黄浦区教育学院 上海 200023)
笔者对平面向量数量积的一些应用进行了初步探讨.主要涉及以下3个方面:在距离问题中的应用、在向量等式问题中的应用、在最值问题中的应用.文中通过若干典型例题的解析,来阐述这些应用的操作方式、具体特点与独特优势.
平面向量;数量积;应用
关于平面向量数量积的应用,比较常见的是平面图形中的夹角(含平行与垂直)问题,这方面的研究已比较多.而对于其他方面的一些应用,相关研究还比较少.下面就对这些应用进行初步探讨,供同行们教学时参考.
1 在距离问题中的应用
在平面几何与平面解析几何中,有许多距离问题,可以用向量的数量积运算来解决.


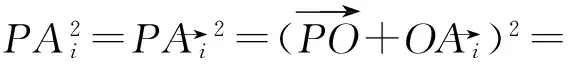

其中i=1,2,3,4,5,可得



例2[1]证明:正多边形内任意一点到各边所在直线距离之和为定值.
分析 正多边形内任意一点到各边距离可转化为数量积,然后证明这些数量积的和为定值.
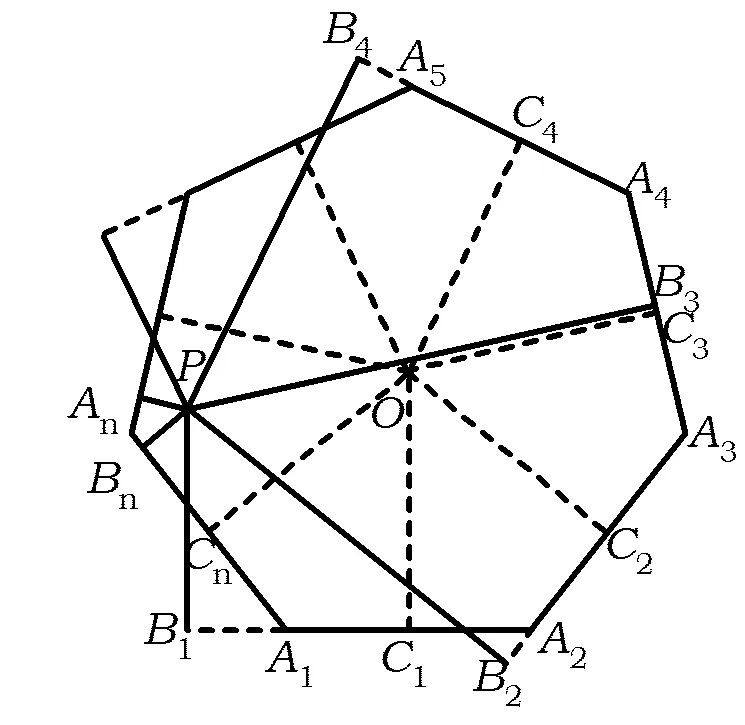
图1
证明 如图1,设P为正n边形A1A2…An所在平面内的任一点,Ci(其中i=1,2,…,n)是边AiAi+1(其中An+1=A1)的中点,点P到边AiAi+1(其中An+1=A1)的距离为di,O是正n边形的中心,r是其内切圆的半径,则



因此,正多边形内任意一点到各边所在直线距离之和为定值.
说明 在空间几何中,我们常用空间向量的数量积来计算距离,如点面距离、异面直线距离等.而在平面上,我们同样可以用平面向量的数量积来计算点线距离.本题中的点线距离可以看成向量投影的绝对值,而一个向量在另一向量上的投影值就是一个向量与另一向量的单位向量的数量积.将点线距离转化为数量积之后,就可以运用向量运算的有关法则来解决问题.
例3 如图2,设AC是ABCD的较长的对角线,过点C作直线AB,AD的垂线,垂足分别为E,F,试求证:AB·AE+AD·AF=AC2.
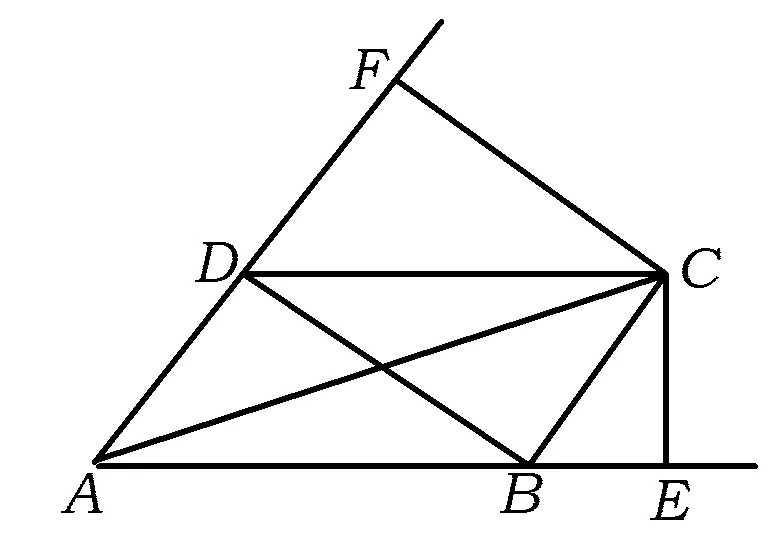
图2
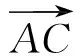
解 由CE⊥AB可得


又四边形ABCD是平行四边形,从而

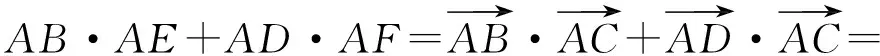

说明 本题也可以用平面几何或解析几何的方法进行证明,但明显较上述向量法来得繁琐,从中我们可以体会到向量法的优越性.另外,向量法在解决平面几何与解析几何问题中,具有较为广泛的应用,而不仅仅是夹角(含平行与垂直)类问题.
2 在向量等式问题中的应用
近年来的高考或竞赛试题中,经常出现一类向量等式问题.这类问题处理方法很多,但不同方法繁简程度差异较大.下面我们尝试利用向量的数量积来进行求解.
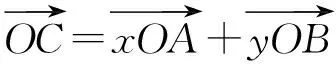

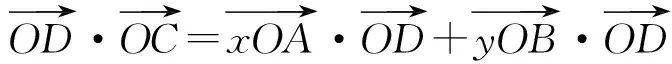
可得

说明 在本题中,当点C与点A或点B重合时,x+y取得最小值,且最小值为1.本题的处理方法很多,但有些方法解题过程较为繁琐.上述解法不仅过程简洁,而且自然流畅,很好地展现了问题的本质.

图3 图4

分析 △AOB与△AOC的面积比等于点B,C到直线AO的距离之比,而点线距离可以用向量数量积来加以讨论.
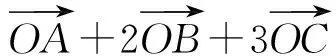

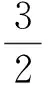
说明 与例2一样,本题也是将点线距离转化为向量的数量积.这种处理方法非常简便,并且利用这种方法可以很容易地将上述结论加以推广.
3 在最值问题中的应用
利用向量工具也可以解决一些代数中的最值问题、不等式问题、线性规划问题.其求解的关键是将这些代数问题转化为关于向量的数量积问题.


图5
且m≥0,n≥0.如图5,在坐标系mOn中,点(m,n)的轨迹是以原点为圆心、以3为半径的圆在第一象限以及2个坐标轴正半轴上的部分.
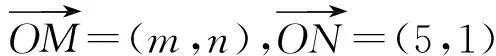


说明 应用向量数量积有效地实现了数形结合,使解题过程与相应结论一目了然.
例7[2]设z=2x+y,变量x,y满足条件
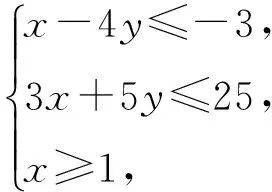
求z的最大值和最小值.

图6
分析 因为z=2x+y=(2,1)·(x,y),所以z可看成2个向量的数量积,可应用向量数量积的几何意义来解决.
解 作出可行域如图6.设N为可行域内的任意一点,M(2,1),则


说明 利用向量的数量积来解决线性规划问题,解题思路也较为清晰和直观.
4 在三角问题中的应用
向量与三角有密切的关系,因此我们也可以利用向量的数量积来解决三角问题,并且同样具有简捷、明快等特点.


图7
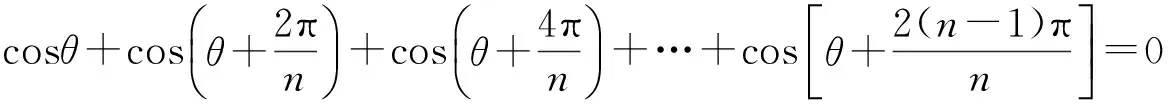
说明 本题若不利用向量的数量积,也可采用向量的其他知识来求解.例如可构造以坐标原点O为圆心、半径为1的圆的内接正n边形(其中一个顶点坐标为(cosθ,sinθ)),由其重心的横坐标为0,也可得到相应结论.
总之,向量是数形结合的重要桥梁,是解决各种数学问题的有效工具.为此,在高中数学教学过程中,应高度重视向量及其数量积的教学,并逐步加强向量应用方面的教学,切实发挥好向量的桥梁与工具作用.
[1] 寇恒清.正多边形的一个性质的简证与再推广[J].数学通报,2014(11):58-59.
[2] 胡云浩.向量数量积的几何意义应用例析[J].中学数学杂志,2006(3):32-34.
�2015-10-13;
2015-11-09.
寇恒清(1966-),男,江苏赣榆人,中学高级教师,研究方向:数学教育.
O123.1
A
1003-6407(2016)03-21-03
