你分我来补 一招显原形——巧用割补法解决棱锥问题*

●许钦彪

(稽山中学 浙江绍兴 312000)



你分我来补 一招显原形
——巧用割补法解决棱锥问题*

●许钦彪

(稽山中学 浙江绍兴 312000)

立体几何是高中数学的重要内容，也是高考的主要和必考内容.从全国各省市历年高考试题统计分析，立体几何综合解答题中许多是与棱锥有关的综合问题.如果能分析清楚这类问题的命题依据、背景和来源，对解决这些棱锥问题是很有益处的.认清棱锥问题的来源，将其还原为规则几何体，再予解决的方法——“割补法”对于解决棱锥问题具有重要的意义和作用.

棱锥;分割;添补

立体几何是高中数学的重要内容，也是高考的主要和必考内容.从全国各省市历年高考试题统计分析，每年必有一个立体几何综合解答题，其中许多是与棱锥有关的综合问题.如果能分析清楚这类问题的命题依据、背景和来源，对解决问题是很有益处的.

我们先从2个常见的棱锥问题入手分析.

问题1 如图1，三棱锥P-ABC的3条侧棱PA，PB,PC两两垂直，且长度分别为3，4，5，求该三棱锥的外接球的表面积.

图1 图2

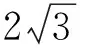
从学生解答的情况看，普遍存在着解答过程冗长、说明不清、计算复杂等问题，导致不能正确完整地解决.究其原因，是对这类棱锥问题的命题来源不了解，感觉陌生困难，从而找不到正确、合理、快捷的解决方法.事实上，这种棱锥都是相应的长方体分割得到的，因而，把其添补还原成相关的长方体，问题就会变得熟悉而简单，从而迎刃而解.

1)把所给三棱锥添补成相应的长方体(如图3)，其外接球就是该长方体的外接球，直径是对角线之长

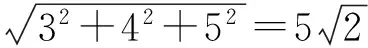
球的表面积为

图3 图4

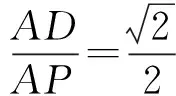
由此可见，认清棱锥问题的来源，将其还原为规则几何体，再予以解决的方法——“割补法”对于解决棱锥问题的重要意义和作用.事实上，许多棱锥是由规则的长方体或正方体等分割得到的，这些棱锥综合问题其来源和命题素材是相应的长方体或正方体.理解了这类问题的背景和本质，就可以尝试把棱锥添补还原成相应的长方体或正方体，从而将其化为熟识的长方体、正方体问题来解决.

本文以几则高考立体几何综合题来说明如何巧用“割补法”解决棱锥综合问题.

(2008年浙江省数学高考理科试题)

图5 图6

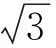
可见，巧用割补法把棱锥还原为相应的正方体后，问题变得简单熟悉，解答就更准确、快捷，其事半功倍的效果显而易见.

例2 若四面体ABCD的3组对棱分别相等，即AB=CD，AC=BD，AD=BC，则以下结论正确的是______.

①四面体ABCD每组对棱互相垂直；

②四面体ABCD每个面的面积相等；

③从四面体ABCD每个顶点出发的3条棱两两夹角之和大于90°而小于180°；

④连接四面体ABCD每组对棱中点的线段互相垂直平分；

⑤从四面体ABCD每个顶点出发的3条棱的长可作为一个三角形的3条边长.

(2012年安徽省数学高考理科试题)

分析 如果仅根据题意得到的棱锥看，由于要判断的结论多且涉及面广，问题就会感到陌生而困难.作为高考的一个填空题，时间上也必须快速.根据当年的高考评卷分析，此题失分的考生较多，其原因就是因为不能认识到该题的来源本质，只在棱锥上考虑，从而找不到正确简洁的方法.如果认识到了棱锥的来源本质，就会联想到长方体的3组对面对角线分别相等，认识到该棱锥是由长方体分割得到的，可以把它添补为相应的长方体(如图7)，问题就化难为易，化陌生为熟悉了.

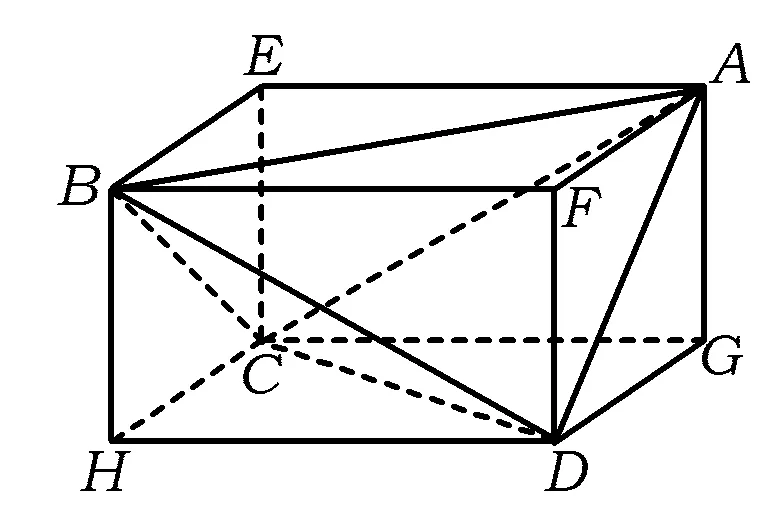
图7

在长方体中容易判断出：

①不正确；

② 4个三角形的3条边长均相等，正确；

③若每个顶点3个夹角之和均小于180°，则4个顶点的夹角之和小于720°，而事实上，4个顶点的夹角之和(12个角)就是4个三角形面的角度之和等于720°，矛盾，不正确；

④每组对棱中点连线实际上就是长方体每组对面的中心连线，这3条线段交于长方体中心且垂直平分，正确；

⑤每一个顶点的3条棱其中2条棱是夹边，第3条与对边等长，如AB,AD为夹边，AC和BD等长，而ABD是三角形，AB,AD,AC长当然也可以构成三角形，正确.

例3 如图8，三棱锥P-ABC中，PA⊥平面ABC，PA=1，AB=1，AC=2，∠BAC=60°.

1)求三棱锥P-ABC的体积；

(2015年安徽省数学高考理科试题)

图8 图9

例4 如图10，四边形ABCD是边长为1的正方形，MD⊥面ABCD，NB⊥面ABCD，且MD=NB=1，E为BC的中点.

1)求异面直线NE与AM所成角的余弦值.

2)线段AN上是否存在点S，使得ES⊥面AMN？若存在，求出线段AS的长;若不存在，请说明理由.

(2009年福建省数学高考理科试题)

图10 图11

分析 据题意可知，此命题源于正方体，还原为棱长为1的正方体(如图11)后，就化为熟悉的正方体问题了.

从而

2)若ES⊥面AMN，则有ES⊥AN，即ES在正方体前面的射影BS⊥AN，此时S必为AN的中点，ES在正方体上面的射影(S′,E′必为所在棱的中点)E′S′⊥MN，即ES⊥MN.

图12

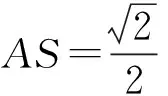
例5 在如图12所示的几何体中，四边形ABCD是正方形，MA∥PD，MA⊥平面ABCD，AD=PD=2MA,E,F,G,H分别是MB,PC,PB,PA的中点.

1)求异面直线EF与PA所成角的余弦；

2)求平面EGF与底面ABCD所成二面角的大小；

3)求平面EGF与平面DHF所成二面角的余弦值.

(2010年山东省数学高考试题改编)

分析 此命题从给出的已知图中较难找出所求的线、面之间的关系.考虑到题设条件，可将其添补还原为如图13所示的正方体，就较易得出相互之间的关系.

如图13中，作正方体中截面INQR，显然E,G,F在该平面内.

图13 图14

1)取PD,MA的中点K,S，则EF∥SK.问题就化为在左侧平面正方形(如图14)中，求SK与对角线PA所成角的余弦，再设O为KD的中点，则所求角化为更简单易求的∠PAO.

设正方体的棱长为1，则

2)面EGF就是中垂面INQR，显然面EGF与底面ABCD所成角为90°.

3)面EGF与面DHF所成的角就是面DHF与中垂面INQR所成的角θ.由图14易知△DHF在中垂面上的射影就是△NGF.

由射影面积公式得

�2015-12-29；

2016-01-19.

许钦彪(1962-)，男，浙江绍兴人，浙江省特级教师，研究方向：数学教育.

O123.2

A

1003-6407(2016)03-08-03