圆锥曲线离心率的求解策略*

●王新宏

(张掖市实验中学 甘肃张掖 734000)



圆锥曲线离心率的求解策略*

●王新宏

(张掖市实验中学 甘肃张掖 734000)

圆锥曲线的离心率是高考的热点内容，而且常考常新，值得我们关注；通过总结求解圆锥曲线离心率的关键与规律，让读者清楚求解离心率主要是通过各种途径构建关于a,b,c(或a,b,c中的2个)的一个等式或不等式；真题示范，引导他们灵活运用“关键与规律”，快速准确地求解离心率或与之相关问题.

离心率；值；范围；关键；方法；转化

圆锥曲线的离心率是解析几何中的重要内容，也是高考考查的热点之一.圆锥曲线的离心率问题解法有多种，如果我们能掌握规律，抓住关键，就能轻松、快速地解决相关问题[1].那么，关键是什么，规律又有哪些呢？

1个关键：寻找、寻求建立a,b,c(或a,b,c中的2个)的一个等式或不等式.

2个切入点：从“形”入手、从“数”下手.

3个方向：从圆锥曲线的定义思考、从几何图形的性质出发、从方程(或不等式)的角度落笔.

4种工具：平面几何基础知识、平面向量的知识、三角函数、柯西不等式.

5种思想：数形结合的思想、方程思想、函数思想、等价转化思想、分类讨论思想.

1 求离心率的值

图1

根据题目给定的条件，寻找并建立含有a,b,c(或a,b,c中的2个)的一个等式，即可求得离心率.

(2015年山东省数学高考理科试题第15题)

kOB·kAF=-1,

从而

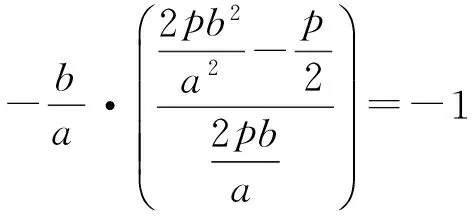
即

5a2=4b2,

得

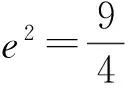
故

点评 画图很重要.若题目较复杂，则需要耐住性子，要清醒地认识到:题易，我易，他易，不大意;题难，我难，他难，不畏难.例1的图形有点复杂，但关键是要找到关于a,b,c(或a,b,c中的2个)的一个等式，沉着冷静，胆大心细，足以应对.

2 求离心率的范围(或最值)

可借助图形、圆锥曲线定义或常见结论等知识寻求解决问题的突破口.

( )

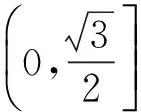
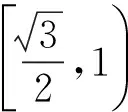
(2015年福建省数学高考文科试题第11题)

解 如图2，设椭圆的左焦点为F1，半焦距为c，联结AF1,BF1,则四边形AF1BF为平行四边形，因此

|AF1|+|BF1|=|AF|+|BF|=4.

根据椭圆定义,

|AF1|+|AF|+|BF1|+|BF|=4a，

图2

点评 例2重点考查考生的等价转化与化归的能力，由|AF|+|BF|=4能否等价转化为4a=8；另一方面草图对解题有不可轻视的指导引领作用.

3 与离心率交汇的其他问题

此类问题要注意全方位、多角度去思考，寻求多方着力，尽可能通过分析推理得出最简便的方法.

( )

(2014年湖北省数学高考理科试题第9题)

图3

解法1 如图3，设|PF1|=r1，|PF2|=r2(其中r1>r2),|F1F2|=2c,椭圆的长半轴长为a1，双曲线的实半轴长为a2，椭圆、双曲线的离心率分别为e1,e2.由余弦定理得

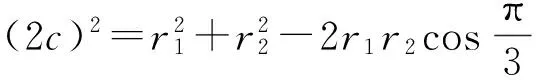
即

又根据定义r1+r2=2a1,r1-r2=2a2，得

r1=a1+a2,r2=a1-a2,

从而

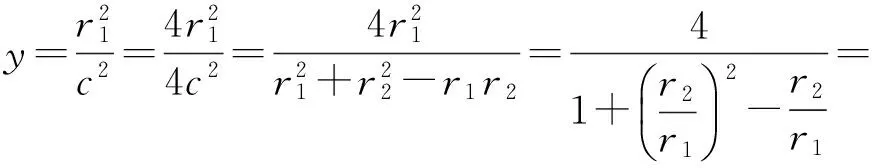
故选A.

解法2 如图3，设|PF1|=r1,|PF2|=r2(其中r1>r2),|F1F2|=2c,椭圆的长半轴长为a1,双曲线的实半轴长为a2,椭圆、双曲线的离心率分别为e1,e2.由定义得

r1+r2=2a1，r1-r2=2a2,

平方得

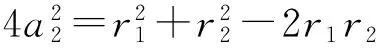
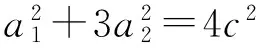
即

因此，由柯西不等式得

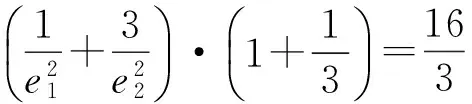
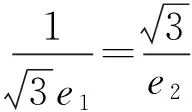
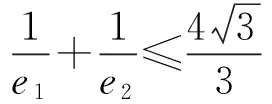
故选A.

点评 二维形式的柯西不等式为

当且仅当a1b2=a2b1时等号成立.

解法3 如图3，设|PF1|=r1，|PF2|=r2(其中r1>r2),|F1F2|=2c椭圆的长半轴长为a1，双曲线的实半轴长为a2，椭圆、双曲线的离心率分别为e1,e2.由余弦定理得

从而

于是

消去r1,r2，得

(1)

以下同解法2.

或构造向量求解如下：

p·q=|p|·|q|cosθ(其中θ=),

所以

|p·q|≤|p|·|q|，

即

|p·q|2≤|p|2·|q|2,

代入式(1)得

即

得

故选A.

解法4 如图3，设|PF1|=r1,|PF2|=r2(其中r1>r2),|F1F2|=2c，椭圆的长半轴长为a1，双曲线的实半轴长为a2，椭圆、双曲线的离心率分别为e1,e2.由正弦定理得

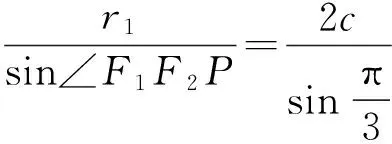
即

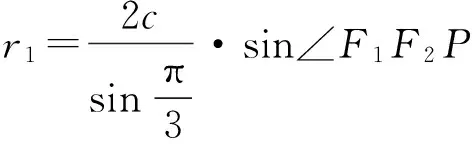
故选A.

解法5 如图3，设|PF1|=r1，|PF2|=r2(其中r1>r2),|F1F2|=2c,椭圆的长半轴长为a1，短半轴长为b1,双曲线的实半轴长为a2，虚半轴长为b2,椭圆、双曲线的离心率分别为e1,e2.由椭圆和双曲线的焦点三角形面积公式得

即

以下同解法2或解法3.

以“形”入手，借助函数、柯西不等式、三角函数、焦点三角形面积公式等，都是为了有效地架起已知与求解之间的桥梁，意在考查考生利用知识等价转化问题、解决问题的能力[2].

[1] 张启兆.解圆锥曲线的离心率问题有讲究[J]．中学生数学，2012(12):16-17.

[2] 李智勇,何涛澜.一道圆锥曲线题的解法探讨[J]．数理天地，2015(7):25-26.

�2015-10-20；

2015-11-16.

甘肃省教育科学“十二五”规划2013年度课题“新课改理念下高三数学复习高效策略研究”(GS[2013]GHB0771).

王新宏(1974-)，男，甘肃高台人，中学高级教师,研究方向：数学教育.

O123

A

1003-6407(2016)03-05-03