支持向量机在化工过程故障诊断中的应用

蒋 强，黄 剑

(沈阳理工大学 信息科学与工程学院，沈阳 110159)



支持向量机在化工过程故障诊断中的应用

蒋 强，黄 剑

(沈阳理工大学 信息科学与工程学院，沈阳 110159)

针对当前复杂的化工过程，提出一种基于主元分析和优化参数支持向量机相结合的故障诊断方法。先采用主元分析法对TEP的5种状态模式进行特征提取和故障监测，若监测为异常，再利用优化参数的支持向量机进一步进行故障诊断。实验结果表明，与单独使用支持向量机方法相比，所提方法克服了单一方法的缺陷与不足，提高了故障诊断的准确率。

主元分析；支持向量机；故障诊断

化工几乎涉及了人类生产生活的各方面，而化工过程的复杂化和大型化也带来了许多安全隐患，如果系统一处发生故障，就有可能引起连锁效应，造成巨大的人员伤亡和财产损失。因此，研究化工过程的故障诊断显得尤为重要。

针对化工过程的特殊性，依斯曼化学品公司开发了一种高级仿真工业过程—田纳西伊斯曼过程(TEP)，众多学者利用它进行化工过程故障诊断的研究[1]。目前，应用于TE过程的故障诊断方法已经越来越成熟，主要集中在多变量统计分析、神经网络、支持向量机等方法[2]。

但是这些方法的故障诊断准确率仍有待提高，本文提出主元分析和支持向量机相结合的方法，利用两种方法的优点提高TEP故障诊断准确率。首先，利用主元分析进行故障监测和特征提取，若监测正常，则继续进行监测，否则采用支持向量机确定异常数据属于哪类故障，最后对支持向量机的相关参数进行优化，进一步提高其故障诊断的准确率。

1 主元分析

主元分析(Principal Components Analysis，PCA)是一种经典的数据降维方法，其提取的主成分可以摒除原始数据空间的冗余信息而保留大量的方差信息，并且各主成分变量相互正交[3]。

1.1 PCA的数据降维

假设样本数据X∈Rm×n，其中m表示样本数，n表示变量数，那么可对X做如下的主元分解：

(1)

式中:[t1t2… tn]表示样本X的得分矩阵，其两两相互正交；[p1p2… pn]表示样本X的负荷矩阵，其两两相互正交且长度为1。

使用累积贡献率的方法选出k个主元构造出主元子空间，这k个主元代表了样本数据最主要的变化，而变化较小的几个主元可以忽略，因此样本X可以近似表示为

(2)

这样，原样本数据X近似为X*，变量数从n个减少到k个，实现了数据的降维。

1.2 PCA的故障监测

基于PCA的TEP故障监测策略是：提取TEP正常状态样本的主元并构造主元子空间，计算主元子空间的T2统计量设为正常状态的控制限，将测试样本投影到主元子空间并计算其统计量，若其超出了正常状态的控制限，则认为系统发生故障，这种方法无需了解系统的结构和原理，建模简单，易于实现[4]。

TEP的样本数据有52维，若将样本直接送入支持向量机进行训练，由于维数过高，计算量较大，势必会影响训练的速度。而PCA方法不但可以实现数据降维，还可以消除变量间的非线性关联，因此可使用PCA方法对TEP样本数据进行故障特征提取，再利用支持向量机进行故障诊断。

2 支持向量机

支持向量机(SupportVectorMachine，SVM)是Vapnik等人提出的一种基于统计学习理论的机器学习方法，它可以将非线性问题转化为线性问题并能得到全局最优解，从而避免了神经网络中经常出现的过学习、欠学习、局部最小化等问题，近年来在故障诊断领域得到了广泛的应用[5-6]。

2.1 两分类SVM

标准SVM是两分类分类器，其结构示意图如图1所示，x=(x1,x2,…,xm)为输入向量。

图1 SVM结构示意图

其基本策略是把输入空间的样本映射到高维特征空间，然后在特征空间中求出把样本线性分开的最优分类面[7]。假设两类样本集(xi,yi),其中，xi∈Rn，yi∈{-1,+1}(i=1,2,…,m)，m为训练样本总数，n为样本空间的维数，yi为样本的类别标签。那么对这两类进行分类时，标准SVM即解决如下问题

(3)

式中：K(xi,xj)为满足Mercer条件的核函数；αi为拉格朗日乘子，上式的解中只有一部分αi不为零，对应的样本称为支持向量(SupportVector，SV)；C是一个大于0的常数，称为惩罚系数。由此构造分类决策函数为

(4)

式中，sign为符号函数，b*为决策函数的阈值。

2.2 “一对一”多分类SVM

故障诊断大多是多分类问题，Kressel提出的“一对一”算法可以实现多分类问题的求解，此方法需要在每两个类别间构造一个分类器。在故障诊断中，若研究对象共有a个故障模式，则需要构造b=a(a-1)/2个分类器，每个分类器训练两种故障模式的训练集，并构造相应的决策函数。对于每个测试样本点而言，b个分类器会给出b个判别结果，统计所有判别结果得到各个类的总票数，得票数最多的类即为该样本点所属的类，这种算法的优点是每个分类问题的规模都很小，每次只需要将两类的训练数据进行训练，训练时间比较短[8]。

2.3 SVM参数优化

Vapnik等人的研究说明，SVM的性能主要取决于误差惩罚因子C和核函数中的参数g[9]，最优的参数可以避免过学习和欠学习状态对分类准确率的影响，但是目前国际上并没有公认最好的参数优化方法。

采用交叉验证(Cross Validation，CV)的方法，可以找到一组相对较好的参数C和g使得训练集达到最高的分类准确率，CV方法有多种，其中K-CV法的基本思想是让参数C和g在某一范围内离散取值，对于取定的C和g，将原始训练集均分成k组，将每个子集作一次验证集，余下的k-1组作为训练集对SVM进行训练，这样就会得到k个验证集的分类准确率，取它们的平均数作为此组C和g下的分类准确率，使分类准确率最高一组C和g即为SVM的最佳参数。

3 实验仿真与结果分析

3.1 样本的建立

本文从网站http://web.mit.edu/braatzgroup/links.html上下载的数据是故障诊断的标准数据集，此数据集包括正常状态和各故障模式下的训练集和测试集。

TE过程共预设了21种故障，其中故障1～7为阶跃、8～12为随机扰动、13为慢漂移、14～15为粘滞、16～20为未知，21为恒定故障。本文选择正常状态、故障6、故障8、故障13和故障18作为故障诊断的研究对象，5种模式的描述如表1所示，将其重新编号为F0、F1、F2、F3和F4，并将其分类标签分别设为0、1、2、3和4。对这5种模式分别选择200组训练集和100组测试集组成最终的训练集1000和测试集500×52，其中1000和500代表样本数，52表示样本点的变量数。

表1 5种模式的描述

3.2 实验仿真

3.2.1 基于PCA的TEP故障检测和特征提取

基于PCA的故障检测步骤如下：

(1)建立正常样本的主元模型：使用TEP正常状态(F0)的200组训练集建立主元模型，通过累计贡献率的方法确定主元的个数。实验中当累计贡献率设置为0.9时，主元个数为29个，即通过PCA降维后原始的52维数据变为29维。

(2)计算正常样本的控制限：计算主元模型的T2统计量，当T2统计的置信度设置为99%时，主元子空间的控制限为：T2UCL=74.5801。

(3)对测试集进行测试：对5种模式共500组测试集进行测试，测试结果如图2所示，图中的红色虚线为主元子空间的控制限。从图2可以看出，前100组正常工况下的数据未超过控制限，而后400组的4种故障数据均超过控制限，可判定为发生故障。因此基于PCA的TEP故障监测准确率达到了100%。

PCA的故障特征提取：将所有训练集和测试集投影到前面确定的主元空间，这样原始的52维数据经降维后变为29维，即完成了PCA的故障特征提取，降维后的样本为X*，将其分为新的训练集和测试集用于SVM故障诊断。

3.2.2 基于PCA_SVM的化工过程故障诊断

实验中SVM 的实现采用台湾大学林智仁教授的LIBSVM工具箱，在Matlab软件平台下运行，此工具箱默认采用“一对一”法支持多分类问题。

图2 主元分析统计量变化图

(1)训练SVM模型。由于降维后的样本X*各维数据量纲不同，因此首先对其数据进行归一化处理，使各维的数据被规整到[0,1]的范围，假设样本X*其中一维数据为x*，则此维归一化后的数据x^为

(5)

将样本X^中的训练集1000×29运用LIBSVM工具箱的相关函数训练SVM，训练过程中使用的相关参数如表2所示。

表2 训练SVM所选参数

表中核函数参数g是默认值，为样本维数的倒数，惩罚系数C默认值为1；由于样本中各类的样本数量相同，因此，各类的权重都设为1。

利用表2中所选的相关参数对SVM进行训练，训练完成的SVM模型如图3所示。图中nr_class表示样本集中有多少个类别，和所设的类别数相同为5个；totalSV代表支持向量的总个数，这里共有644个；nSV表示每类样本的支持向量的数目，样本共有5类，所以它是一个5×1的矩阵；rho是决策函数中阈值b*的相反数，由于采用“一对一”法来解决多分类的问题，因此对于一个5类的样本，共构造了10个决策函数，每个决策函数对应的阈值列于表3中；sv_coef是一个644×4的矩阵，装载的是644个支持向量在决策函数中的系数；SVs是一个稀疏矩阵，装载的是全部644个支持向量。

model=

由于SVM的模型选择为C-SVC，核函数选择为RBF，故每两个类别间的决策函数变为

(6)

式中：n代表支持向量的个数；Wi=yiαi=sv_coef(i)为决策函数的系数；gamma是所选参数g，其大小为0.0345；xi表示支持向量；x是待测试标签的样本。根据式(6)和model中的所得参数，即可确定10个SVM模型的决策函数。

(2)测试集的预测。将样本X^中的500组测试集送入训练好的SVM模型中，得到测试集的预测标签，统计预测标签和期望标签一致的个数记为d，计算分类准确率。

(7)

分类准确率反映了SVM模型对预测集预测的准确性，在本实验中反映了其对各故障的识别能力。

为验证PCA_SVM方法的优异性，将原始样本X采用相同的方法对SVM进行训练并得到测试集的分类准确率，两种方法的预测结果如图4所示，其中图4a为原始测试集的预测结果，图4b为PCA_SVM测试集的预测结果。

图4 SVM和PCA_SVM预测结果

从图4可以看出，PCA_SVM方法较单一的SVM方法对测试集预测准确率更高，即对故障的识别率更高，因此PCA_SVM方法更适合于化工过程的故障诊断。

(3)SVM参数优化。实验中采用K-CV法对PCA_SVM模型的相关参数进行优化，优化结果如5图所示，最佳参数C=256，g=0.57435。将优化的参数用于PCA_SVM模型中，得到最终的故障识别结果如图6所示，经过优化后PCA_SVM的分类准确率达到91%，高于之前的两次识别准确率。

3.3 结果分析

各方法故障诊断准确率的对比结果如表4所示，从表4可以看出，经过PCA特征提取再进行SVM故障诊断的方法比单一使用SVM的方法更好，而经K-CV法参数优化后，PCA_SVM法的故障诊断准确率得到了显著提高。

图5 SVM参数优化

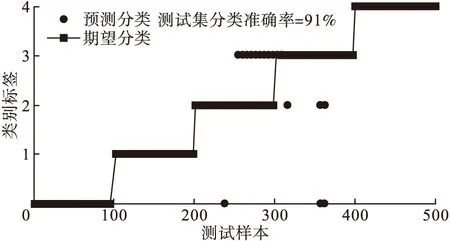
图6 优化参数后的PCA_SVM预测输出

故障诊断方法SVMPCA_SVM参数优化PCA_SVM准确率70.4%80.2%91%

4 结论

通过实验仿真结果可以看出，单一SVM法的故障识别率为70.4%，PCA_SVM法故障识别率为80.2%，故障识别率提高了9.8%，而经参数优化后的PCA_SVM法故障识别率为91%，故障识别率又提高了10.8%，为3种方法中故障识别率最高的一种。因此，经参数优化的PCA_SVM法的故障识别率较单一的SVM法和PCA_SVM法有较大程度的提高，更适合应用于TEP的故障诊断。

[1]王鲜芳,王岁花,杜昊泽,等.基于模糊粗糙集和支持向量机的化工过程故障诊断[J].控制与决策,2015(2):353-356.

[2]张姮.TE过程故障诊断方法比较研究[D].沈阳:沈阳理工大学,2014.[3]童楚东.基于特征提取与信息融合的工业过程监测研究[D].上海:华东理工大学,2015.

[4]薛永飞.基于改进T-PLS的化工过程故障诊断研究[D].兰州:兰州理工大学,2014.

[5]GE M,DU R,ZHANG G C,et al.Fault diagnosis using support vector machine with an application in sheetm etal stamping operations[J].Mechanical Systems & Signal Processing,2004(18):143-159.

[6]ZHANG Y W.Enhanced statistical analysis of nonlinear processes using KPCA,KICA and SVM[J].Journal of Chemical Engineering Science,2009(64):801-811.

[7]沈怀荣,杨露,周伟静,等.信息融合故障诊断技术[M].北京:科学出版社,2013:151.

[8]陈铭.基于LS-SVM的复杂工业过程故障诊断方法研究[D].南京:南京理工大学,2009.

[9]徐晓明.SVM参数寻优及其在分类中的应用[D].大连:大连海事大学,2014.

(责任编辑：马金发)

The Application of Support Vector Machine in the Fault Diagnosis of Chemical Process

JIANG Qiang,HUANG Jian

(Shenyang Ligong University,Shenyang 110159,China)

A fault diagnosis method based on principal component analysis and support vector machine is proposed for the complex chemical process.Feature extraction and fault detection of five kinds of chemical process fault mode is analyzed by using principal component method.If the detection is abnormal,samples of fault classes could be tested by using SVM for fault diagnosis.Experimental results show that the fault diagnosis method overcomes the defects of single method and improves fault diagnosis accuracy based on PCA and SVM in comparison with SVM method.

PCA；SVM；fault diagnosis

2015-07-03

蒋强(1974—)，男，副教授，研究方向：先进控制理论与应用、故障诊断。

1003-1251(2016)05-0028-05

TP29

A