遗传算法优化的开关磁阻电动机RFNN位置控制器设计

乔维德

(无锡开放大学，无锡 214011)



遗传算法优化的开关磁阻电动机RFNN位置控制器设计

乔维德

(无锡开放大学，无锡 214011)

为克服开关磁阻电动机严重的非线性、时变性及强耦合性等缺陷，设计一种递归模糊神经网络控制器，应用遗传算法优化控制器参数，并代替开关磁阻电动机控制系统的位置控制器，对开关磁阻电动机进行准确的位置控制。仿真与实验结果证明设计的位置控制器优于常规PID控制器，具有较强的跟踪能力和动态响应。

开关磁阻电动机；遗传算法；RFNN；位置控制

0 引 言

开关磁阻电动机(以下简称SRM)具有电机结构简单、起动转矩大、调速性能好、运行效率高等优点，特别对于低压、小功率以及恶劣的工作环境，其性能要远好于一般异步电动机和直流电动机，目前已获得广泛应用。然而SRM的磁路分布存在严重非线性，SRM伺服控制系统实际上是多变量、非线性、强耦合的时变系统，传统的线性控制(如常规PID控制)很难满足SRM控制系统的需求。考虑SRM伺服控制系统特性，提出递归模糊神经网络(以下简你RFNN)控制器的设计策略，取代SRM伺服控制系统位置环中的常规PID控制器，且利用免疫遗传算法(以下简称IGA)优化和调节RFNN控制器的结构参数，实现对SRM准确定位的优化控制。

1 SRM数学模型

SRM的定子和转子铁心采用双凸极结构。因SRM磁路高度非线性分布，很难求出精确的数学表达式。通过对SRM磁路的有限元分析与演算，得出SRM的电压、转矩及机械运动等状态方程式。

电压方程：

式中:Uk,Rk,ik,ψk分别是SRM的第k相绕组电压、电阻、电流、磁链。

转矩方程：

式中:Wk,Tk分别是SRM第k相的磁场储能和电磁转矩；θ为转子位置角；Ttotal为总电磁转矩(即各相转矩之和)。当电流为常值时，SRM的电磁转矩Tk可通过磁场储能Wk对转子的位置角求得。

机械运动方程：

式中：J是转动惯量；B是摩擦系数；TL是负载转矩。

以上公式描述了SRM电磁及力学关系，但是由于SRM电机磁矩和转矩方程等具有较强的非线性，实际上难以应用并实现。

2 SRM伺服控制系统设计

2.1 控制系统结构

SRM伺服控制系统由速度环、电流环、位置环三部分组成，电流环采用比例(P)调节控制器，速度环设计为比例—积分(PI)控制器，位置环处在SRM控制系统结构的最外环，各种干扰信号在系统速度环与电流环中形成的误差通过位置环的控制作用加以有效补偿或者抑制。SRM伺服控制系统结构中，给定位置用角位移θr表示，实际位置检测值用θ表示；设计RFNN控制器取代常规PID控制器，用作SRM伺服控制系统位置环中的位置调节器，通过IGA在线调节和优化RFNN的结构参数，如图1所示。

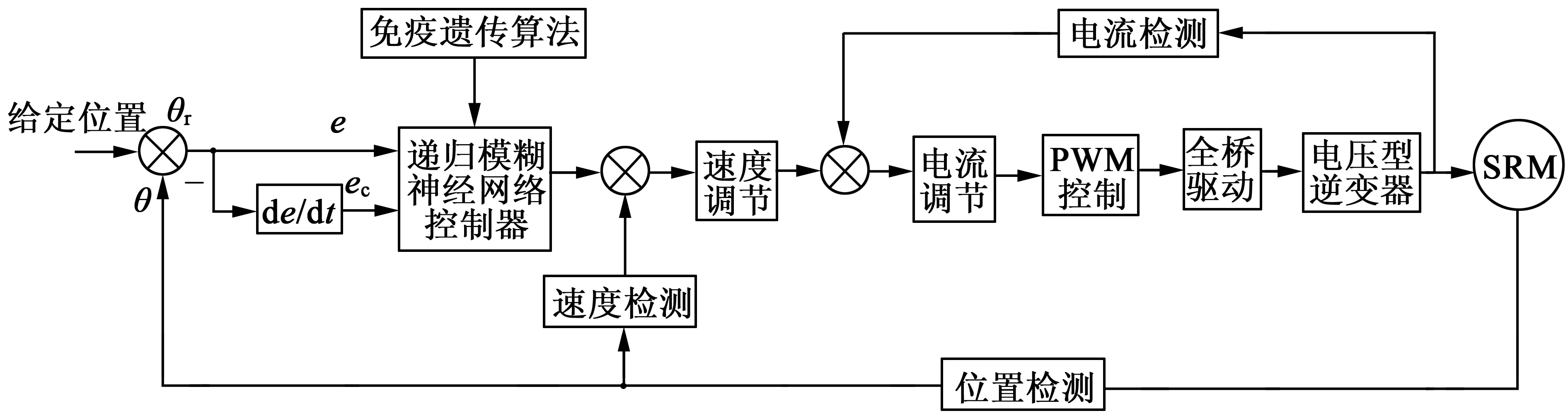
图1 SRM伺服控制系统结构图

2.2 RFNN控制器

RFNN控制器的结构如图2所示。它共有4层BP网络，分别是输入层、模糊化层、模糊规则层、输出层，且在模糊化层加入递归神经元。递归神经元能实现内部信息的反馈连接并及时保存信息，RFNN的输出既与当前输入有关，还与过去的输入和输出有关，以形成局部或全局递归的网络结构，可以通过较快收敛速度和较少神经元个数，有效解决SRM伺服控制系统的高度非线性映射缺陷。

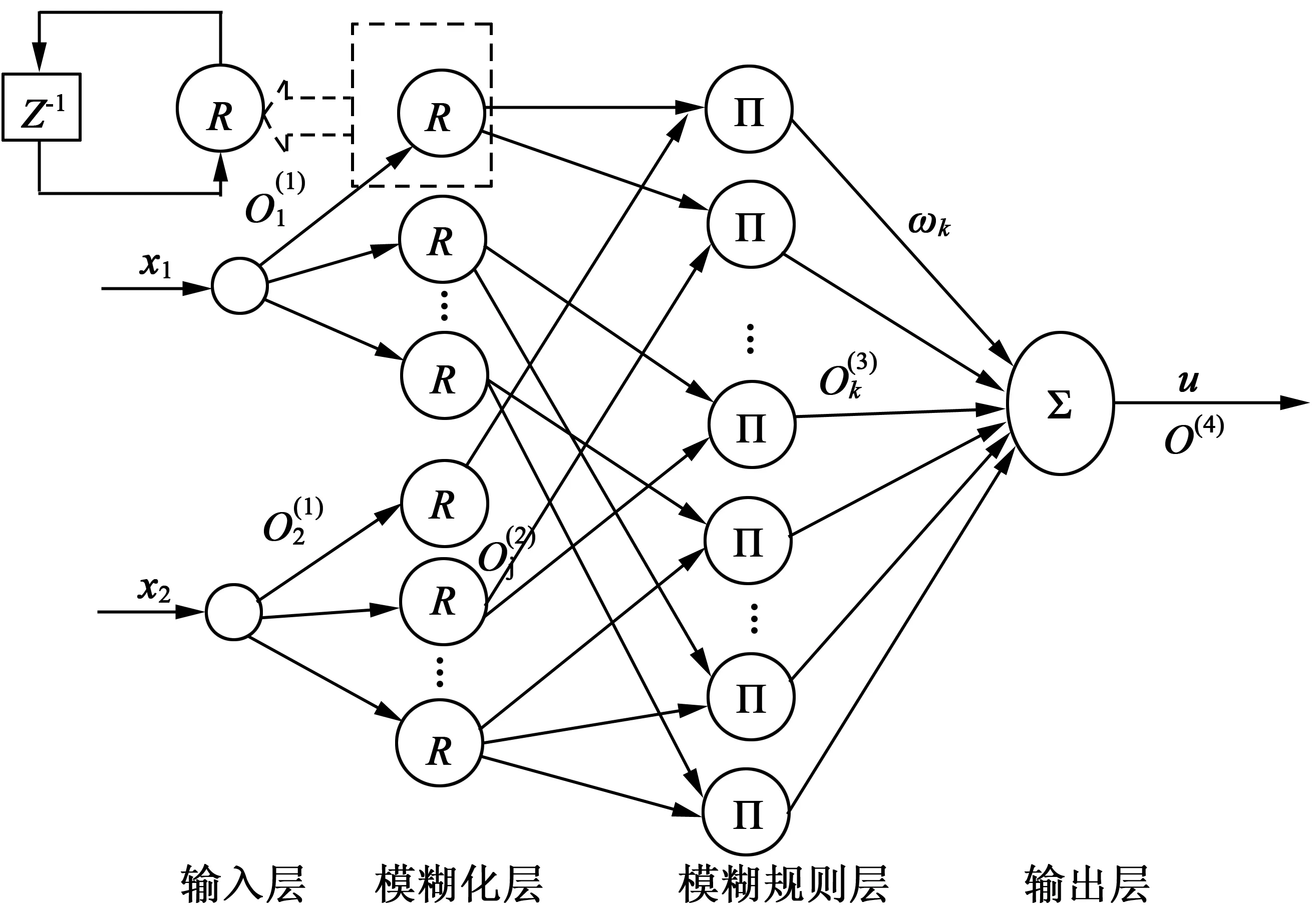
图2 RFNN控制器结构图

在输入层中，网络的输入矢量x为[e，ec]T，将输入量x转换为[-1，1]区间值。

输出节点值：

在模糊化层中，对输入变量进行模糊化处理，每个输入变量均分别表示为模糊语言变量{PB，PS，ZE，NS，NB}，其中，PB为负大，PS为负小，ZE为零，NS为正小，NB为正大。计算求取每个输入分量属于各模糊语言变量集合的隶属度函数，用高斯基函数表示隶属函数。该模糊化层共有10个输出节点，其输出值：

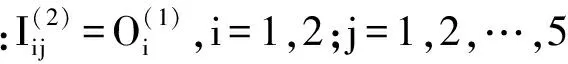
因在模糊化层中的每一个节点均引入同结构的递归环节节点，所以该层输入节点值应：

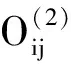
其中，k1=k2=1,2,…,5;k=k1k2=1,2,…,25。

模糊规则层的输出节点值：

在输出层中，首先要对模糊规则层的输出模糊值进行去模糊化和归一化处理。该层的输入和输出值分别：

式中：ωk是模糊规则层与输出层间的连接权值。

2.3IGA优化RFNN控制器参数

IGA是一种基于生物免疫机理的改进遗传算法和智能计算策略，它是在标准遗传算法中注入了生物免疫系统的抗原识别、抗体多样性、免疫记忆、浓度控制等优势功能，能提高遗传算法的搜索速度和全局搜索能力，增强其自我调节功能，从而克服标准遗传算法求解容易陷入局部最优解的缺陷。

在SRM伺服控制系统中，RFNN控制器用作系统的位置调节器，以给定位置值dr与检测位置值d之间的误差e及误差变化率ec作为RFNN控制器的两个输入变量，采用IGA在线优化RFNN控制器的结构参数，即模糊规则层与输出层之间的连接权值ωk、模糊化层中的高斯函数中心值aij、宽度bij及其递归单元连接权值rij、模糊化层与模糊规则层之间连接权值ωjk。通过IGA对RFNN的学习和训练，在线优化控制器结构参数，有效提高RFNN控制器的控制性能和鲁棒性。

3 IGA控制算法实现

第一步，把给定特求问题当作抗原，通过分析特征信息，选择需要优化的参数变量aij, bij,ωk, rij。

第二步，选择IGA运行参数，确定群体规模为50，交叉概率为0.8，变异概率为0.2。

第三步，生成初始群体(即抗体)且进行编码。假设为记忆中抗原，可以从记忆细胞中直接选取对应抗体形成初始群体，不然的话就随机组合产生初始群体。采用十进制编码方式进行编码，形成基因码串，每个码串分别表示一个个体，代表待优化问题的每个解。本文中SRM伺服控制系统需要选取数组(aij, bij,ωk, rij)作为每个抗体对应的RFNN结构参数，初始抗体群体共计有m组(aij, bij,ωk, rij)。

第四步，计算抗体适应度。因为生物进化仅会向适应度函数值增大方向演变，所以适应度函数与目标函数互为倒数。假定抗体Ps对应的RFNN能量函数是Es，因此适应度函数Fs计算表达式：

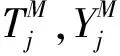
第五步，演变记忆细胞。如果为新产生的抗原，就将当前种群中适应度函数值高的抗体取代记忆细胞中适应度函数值低的抗体；不然的话，把当前种群中适应度高的抗体直接归进记忆细胞。

第六步，抗体促进与抑制。通过相近抗体数和群体总数的比值计算，确定当前种群中适应度值相近的抗体浓度，如果抗体浓度较高，就必须降低抗体的选择概率，以抑制抗体；反过来就应该提高抗体的选择概率，从而通过促进抗体生成使种群个体多样化。

第七步，抗体交叉和变异。根据选取的交叉概率和变异概率进行交叉与变异操作处理，且对生成的新一代种群进行重新评价、选择、交叉、变异，循环重复，持续提升群体最优抗体适应度函数值和平均适应度函数值，直到最优抗体适应度函数值满足预定要求，或者最优抗体适应度函数值和群体抗体平均适应度函数值不能继续提高，而且仍满足控制系统的所有约束条件，由此得出系统的迭代过程收敛并输出RFNN控制器的最优结构参数。

4 仿真研究

采用常规PID控制器和本文设计的RFNN控制器作为SRM伺服控制系统的位置调节器，利用MATLAB软件中Simulink功能，建立SRM控制系统的仿真模型。SRM参数如下：定子极数为6，转子极数为4，额定电压250 V，定子电阻0.78 Ω,额定转速1 200 r/min，转动惯量为0.05 kg·m2。在给定输入信号分别是方波、正弦波时，SRM伺服控制系统在传统PID和RFNN两种位置控制器情况下的位置响应曲线如图3和图4所示。从图3、图4中分析可知，与PID控制器相比，RFNN控制器作用下的SRM控制系统响应速度更快、超调更小、稳态精度更高、抗扰动能力更强、鲁棒性更强。

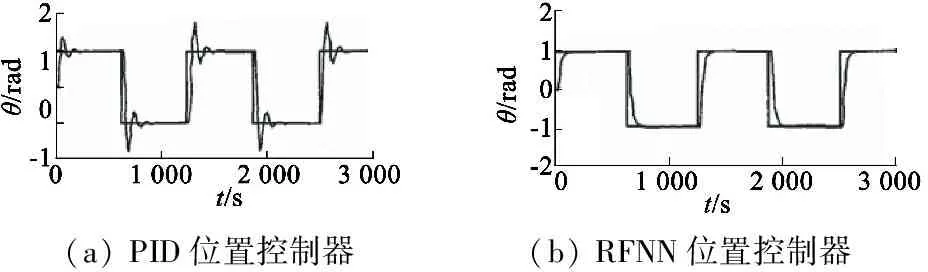
(a)PID位置控制器(b)RFNN位置控制器

图3 给定输入为方波时位置仿真响应

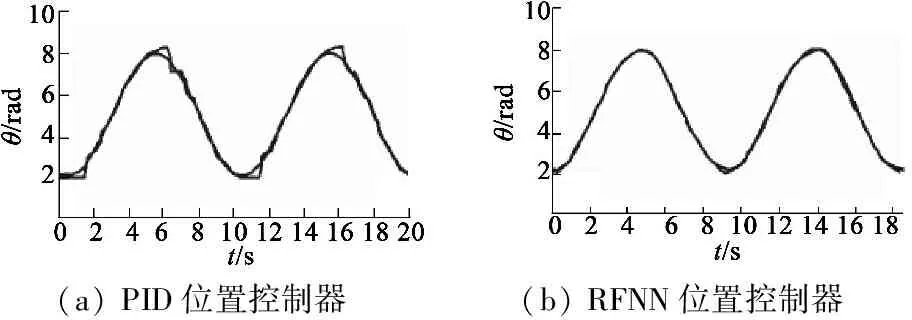
(a)PID位置控制器(b)RFNN位置控制器

图4 给定输入为正弦波时位置仿真响应

5 试验验证

为验证本文设计的RFNN控制器的有效性与可行性，在以DSP芯片为核心的实验平台上对SRM伺服控制系进行带载运行试验，搭建的控制系统实验框图如图5所示。其中DSP芯片采用美国TI公司的TMS320LF2407A。本系统由C语言编程实现IGA控制算法。

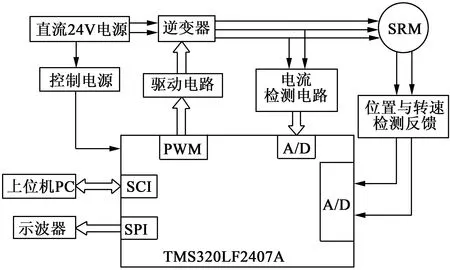
图5 SRM控制系统实验原理框图

图6为实验时给定位置为正弦变化时，位置环采用RFNN控制器策略下的系统位置跟踪响应曲线，从示波器观察曲线分析，其误差非常小，系统的定位控制精度高。

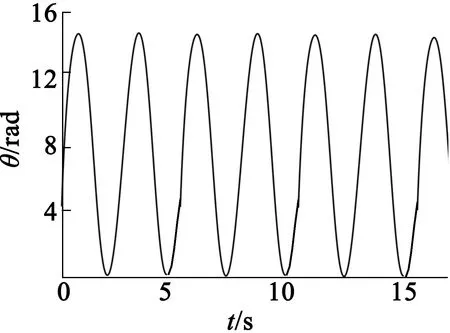
图6 实验给定输入为正弦波时的位置响应

6 结 语

经IGA优化的RFNN控制器应用于SRM伺服控制系统位置调节器，实现对SRM控制系统的定位控制。仿真与实验结果分析表明，RFNN控制器的控制性能明显优越于常规PID调节器，具有较高的位置控制精度和优良的动态响应性能，控制方案有效可行，控制效果较为理想。

[1] 乔维德.遗传优化的模糊免疫PID控制器在SRM中的应用[J].微特电机,2008,36(1):8-10.

[2] 赵子龙,王洪诚,马鹏宇,等.开关磁阻电机单神经元自适应PID控制系统[J].自动化技术与应用,2014,33(6):14-16.

Design of Switched Reluctance Motor’s RFNN Position Controller Optimized by Genetic Algorithm

QIAO Wei-de

(Wuxi Open University，Wuxi 214011)

In order to overcome defects of switched reluctance motor such as serious nonlinear, time-varying and strong coupling, a recurrent fuzzy neural network controller was designed. The genetic algorithm was used to optimize parameters of controller. The designed controller can realize accurate position control of switched reluctance motor instead of the conventional position controller. The simulation and experiment results show that the designed position controller is better than conventional PID controller with strong tracking ability and dynamic response.

switched reluctance motor (SRM); genetic algorithm; RFNN; position control

2015-02-28

TM352

A

1004-7018(2016)02-0075-03

乔维德(1967-)，男，教授，研究方向为电机及其智能控制。