基于CPLD的TRUM相电压平衡控制的研究

孙鹤旭，荆 锴，李国庆，董 砚

(1．河北工业大学，天津 300130；2．河北科技大学，石家庄 050018)



基于CPLD的TRUM相电压平衡控制的研究

孙鹤旭1, 2，荆 锴1，李国庆1，董 砚1

(1．河北工业大学，天津 300130；2．河北科技大学，石家庄 050018)

针对行波型旋转超声电机两相参数不对称带来的两相电压不平衡的现象进行了深入研究。在H桥式电路驱动下，以电机输入LC电路为研究模型，理论分析了输入方波电压占空比与谐振输出电压间的关系，并设计了以CPLD为核心的控制逻辑，实现了对行波型旋转超声电机的驱动电压平衡控制。最后通过对比实验，对两相电压对电机转速转矩的影响进行了验证。

行波型旋转超声电机；两相电压；LC电路；占空比；CPLD

0 引 言

行波型旋转超声波电动机(以下简称TRUM)不同于传统电磁电机，它通过压电陶瓷激发定子弹性体的高频微幅振动，依靠摩擦来驱动转子[1]。这一类电机具有低噪声运行、转矩密度大、瞬态响应快、无电磁干扰、位置分辨率高等特点，在高端精密运动控制中应用前景广阔[2]。TRUM的运行是由两相互差90°的高频正弦电压驱动的，其驱动电压信号通常由推挽式或H桥式驱动电路输出脉宽的方波经升压及LC谐振得到[3-4]。然而，受TRUM两相压电陶瓷材料选取、制造工艺存在差异以及LC谐振电路参数的偏差的影响，两相输入电压往往无法达到平衡，从而导致电机转速和转矩波动大，影响运行效率，严重时还可能损坏电机。文献[5]提出以Boost升压电路作为两相驱动的供电电源，以调节两相电压；文献[6]提出电压闭环的控制方式，动态调整TRUM的两相电压。但闭环的控制方式应用于高频信号时很难满足其动态性能，因此并不能获得良好的调节效果。另外，上述方法均增加了驱动器的硬件结构，不利于电机控制器的小型化设计。

本文基于H桥式驱动电路，研究输出方波信号与电机输入电压间的响应关系，给出两相参数不对称的情况下，平衡两相相电压方波信号的计算方法，并采用CPLD实现TRUM两相电压平衡的开环控制，以简化控制结构。最后通过实验对电压输出和电机性能进行验证。

1 H桥驱动电路

TRUM的H桥驱动电路如图 1所示，两相分别由一个H桥电路连接升压变压器及串联电感构成。

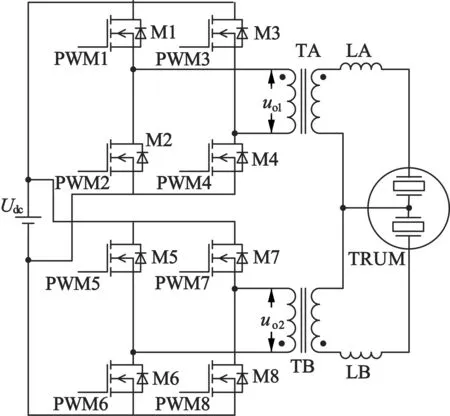
图1 TRUM H桥驱动电路

电路中直流母线Udc恒定，输入开关管的控制信号均满足上下桥臂互反且占空比均为50%。图 2中示出了两个H桥上桥臂驱动信号波形以及H桥输出电压uo1，uo2波形。

图2 H桥PWM控制信号及输出电压

定义输出电压的占空比为其正(负)电平持续时长与半个周期的比值，即图中的α1，α2，两相的占空比可通过调节各相PWM的相位差来实现。控制中通常还要保证两相输出电压正(负)电平的中心轴线互差π/2。

2 LC模型下的TRUM相电压平衡分析

TRUM压电振子可用图 3中虚线框中等效电路表示，通常在谐振工作点出串联支路阻抗较大，电机对外表现为容性，在分析驱动电压时可忽略其串联支路[7]，简化为右图结构，驱动电路中的串联电感L则与一相压电振子等效电容C构成一个LC谐振网络。

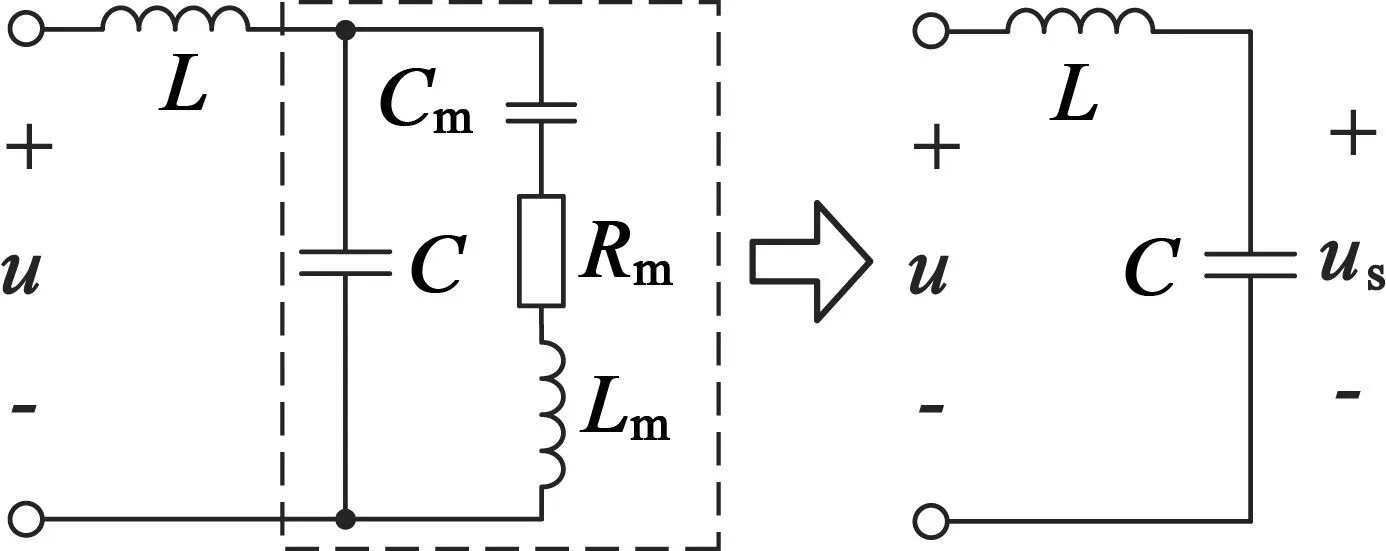
图3 TRUM简化等效电路

升压变压器TA,TB输出与H桥同型的方波电压，取归一化的轴对称方波信号：

(1)

α为占空比。由于该函数为偶函数，其傅里叶展开只包含余弦项：

(2)

(3)

在实际中，受压电陶瓷材料及制造工艺的影响，电机两相输入等效电容并不一致，并且，绕制串联电感时，其电感值也很难做到与期望完全一致。文中所使用的TRUM-60型电机，经导纳圆参数辨识，可得A，B两相的静态电容分别为C1=8.748nF，C2=7.400nF；两相串联电感分别为L1=756.7μH、L2=775.4μH。这样，TRUM两相电压幅值的基波分量与40kHz工作频率下的方波占空比间的关系曲线如图 4所示。

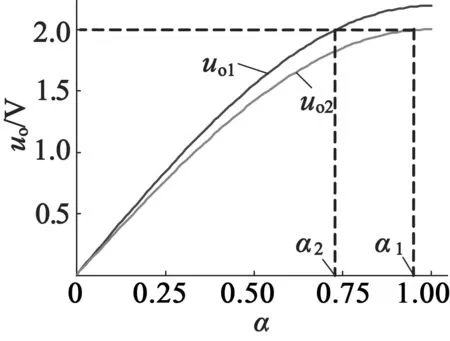
图4 两相电压幅值响应与占空比的关系曲线

于是要想获得等幅值输出的驱动电压，α1,α2存在较大差异。对于以上的电机参数，当B相的α2= 95%时，若获得同样大小的输出电压，A相α1= 73%，谐振放大倍数约2倍。当Udc为20V，升压变压器变比为1∶5，则获得的电机两端的电压为200V。

3 基于CPLD的TRUM相电压平衡控制的实现

控制器硬件结构如图 5所示，以CPLD为核心，结合H桥驱动芯片HIP4081A产生所需的8路PWM。

图5 CPLD控制器硬件结构框图

图5中，CPLD输出的Q0～Q3对应于图中的四个上桥臂PWM信号。PWM信号采用周期计数比较的控制逻辑予以实现，如图 6所示。

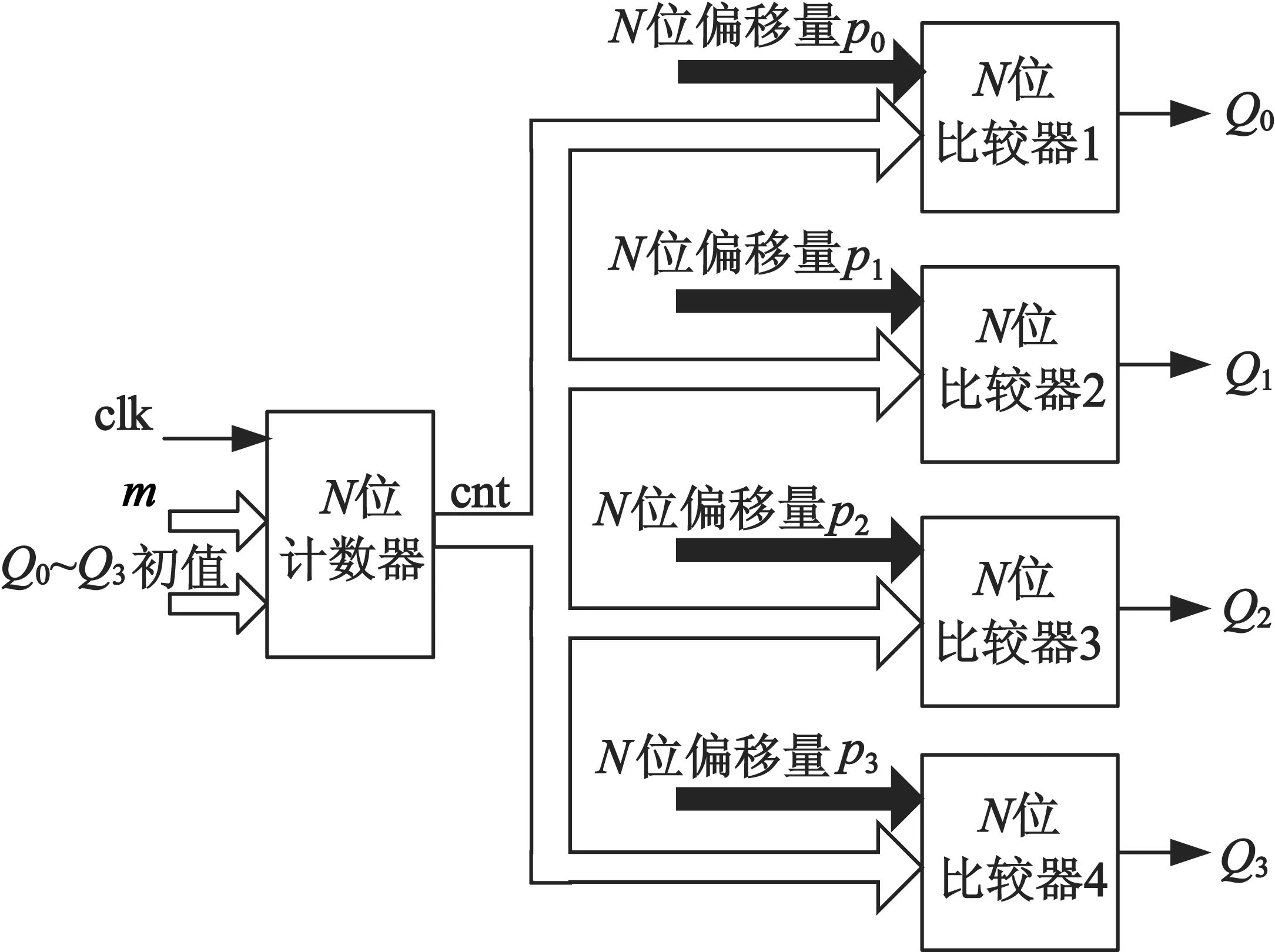
图6 PWM信号生成的CPLD逻辑框图

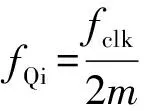
(4)

通常取p0= 0，则可通过代入两相电压平衡所得的占空比，得到偏移量，从而根据控制逻辑输出PWM控制信号控制H桥，使得TRUM的两相驱动电压一致。

4 实验验证

根据上述分析，对两相电压平衡进行对比试验验证。CPLD时钟频率fclk= 40MHz,工作频率fQ=40kHz。当占空比按上节计算得到的α1= 73%，α2= 95%，根据式(4)可得：p0=0，p1=135，p2=305，p0=330。实验中与占空比为1情况进行对比，首先，CPLD输出的PWM信号仿真如图 7所示，图7中左侧为占空比1时的PWM信号，右侧为取α1=73%，α2=95%时的PWM信号。

图7 CPLD信号仿真图

以下的对比实验均基于上述的两种PWM控制信号。当控制信号由CPLD输出，经驱动电路作用于TRUM，最后经LC谐振获得的两相输入电压如图 8所示。

由实验可得，图 8(a)为两相电压不平衡，A相电压峰值约230V，B相电压峰值约208V；图 8(b)两相电压基本一致，峰值约为225V。

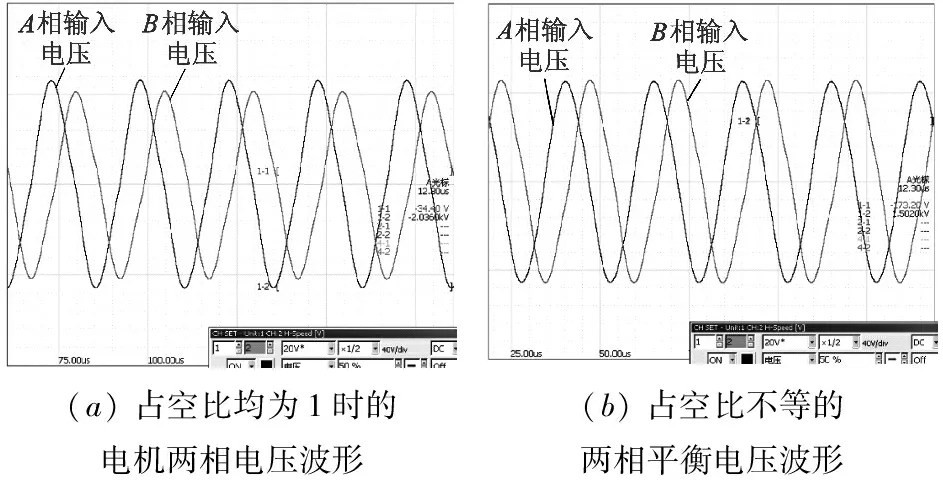
(a)占空比均为1时的电机两相电压波形(b)占空比不等的两相平衡电压波形

图8 电压波形对比图

在上述两种驱动情形下，给电机加载恒定负载转矩，调节电机以同样的平均转速运行，获得其输出转矩和转速曲线，如图 9所示。

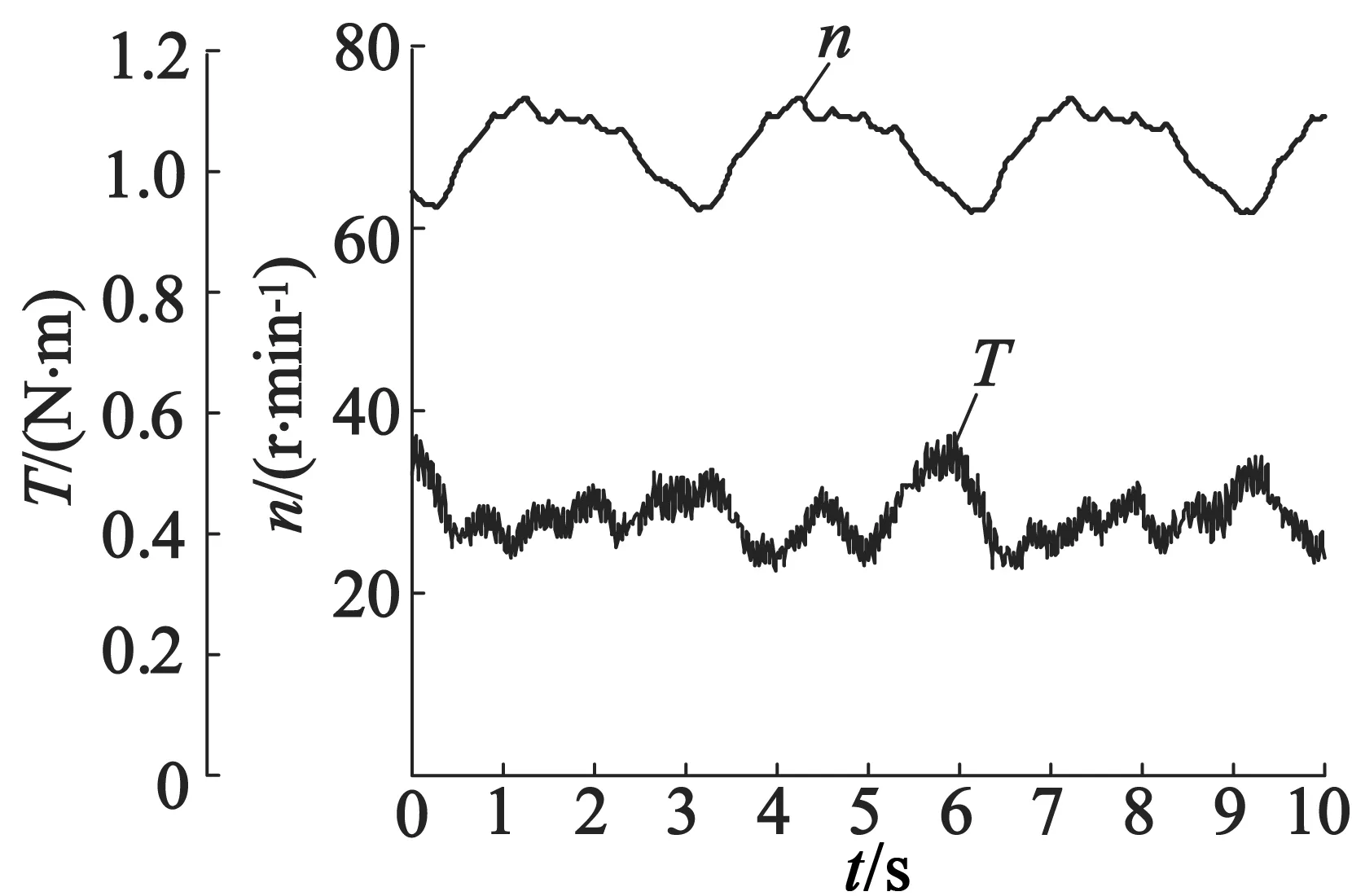
(a) 两相电压不平衡时电机输出转矩和转速

(b) 两相电压平衡时电机输出转矩和转速

图 9(a)为两相电压不平衡情况下的输出转矩和转速曲线，平均转速68.89 r/min，平均转矩0.429 9 N·m，转矩和转速的均方误差分别为0.002 095 (N·m)2,13.89 (r/min)2；图 9(b)为经调整占空比，两相电压平衡后的输出转矩和转速曲线，平均转速67.85 r/min，平均转矩0.433 5 N·m，转矩和转速的均方误差分别为0.001 186(N·m)2,7.209(r/min)2。与前者相比，转速和转矩的波动有所减小,故两相电压平衡有效地降低了电机转矩和转速的脉动，使电机运行更加平稳。

5 结 语

本文针对H桥式驱动电路对TRUM两相输入电压平衡问题进行了研究，以简化的等效电路分析了H桥输出方波电压的占空比与LC谐振输出电压的关系，并据此对两相电压平衡时的占空比进行了求解。文中还以CPLD为核心设计了占空比可控的PWM控制逻辑，并根据两相电压平衡时的占空比计算控制逻辑所需的偏移量。最后通过实验对比了常用恒定占空比下两相电压不平衡及调节后两相电压平衡情况下的电压及输出转矩、转速的波形，验证了本文控制策略对平衡驱动电压确保电机平稳运行的有益效果。

[1] 赵淳生. 超声电机技术与应用[M]. 北京: 科学出版社. 2007.

[2] 李摇霞, 张摇宁, 高摇琳, 等. 超声谐波电动机的设计与分析[J].微特电机,2015, 43(5): 9-13.

[3] YAN Jiajia,RUAN Xinbo.A soft switching driving circuit for ultrasonic motor[C]//IEEE Power Electronics Specialists Conference,2007:559 - 562.

[4] 皮文苑, 鹿存跃, 杨明. 基于NuMicro M0516的超声波电动机驱动电路设计[J].微特电机,2012,40(4):68-70.

[5] 史敬灼.调频调幅调相的超声波电机控制电路[J].微特电机,2008,36(1):46-49.

[6] 王海彦,史敬灼.二相行波超声波电机的电压闭环控制[J].电机与控制应用,2009,36(12):14-16.

[7] 李华峰,赵淳生.基于LC谐振的超声电机驱动器的研究[J].中国电机工程学报,2005,25(23):144-148.

Research for the Phase Voltage Balance Control of TRUM Based on CPLD

SUN He-xu1,2, JING Kai1, LI Guo-qing1, DONG Yan1

(1.Hebei University of Technology,Tianjin 300130,China；2.Hebei University of Science and Technology,Shijiazhuang 050018,China)

The imbalance of the two phase voltage of travelling-wave type rotary ultrasonic motors was studied, which is caused by the asymmetry of the two phases. A theoretical analysis of the phase voltage was done by the LC circuit model to deduce the relationship of the duty cycle of the square wave input voltage and the resonant output voltage, which was under the driving of H-bridge circuit. A control-logic was also designed in CPLD to implement the balance of the two phase voltage. The contrast experiments were completed to testify the effects of the two phase voltage on the speed and torque of the motor.

travelling-wave type rotary ultrasonic motors (TRUM); two phase voltage; LC circuit; duty cycle; CPLD

2015-07-20

河北省自然科学基金项目(E2013202108)；河北省重大科技成果转化项目(13041709Z)；河北省研究生创新资助项目(2015)

TM359.9

A

1004-7018(2016)02-0080-04

孙鹤旭(1956-)，男，教授，博士生导师，研究方向为运动控制、工程系统与控制。