基于变参数MRAS法的异步电机矢量控制研究

黄劭刚,宋凤林,洪剑锋,陈健强

(南昌大学，南昌 330031)



基于变参数MRAS法的异步电机矢量控制研究

黄劭刚,宋凤林,洪剑锋,陈健强

(南昌大学，南昌 330031)

提出一种变参数的MRAS法，该方法采用改进电压模型法磁链观测器作为参考模型，采用变参数PI调节器代替传统的PI调节器，即在电机控制低速段与高速段分别取不同的PI参数，其值随着转速变化而变化。通过对基于变参数MRAS法的异步电机无速度传感器矢量控制系统仿真与实验表明，改进电压模型法可以较好解决积分漂移问题，且控制系统响应速度得到较大提高，尤其是低速时的收敛速度与转速辨识误差得到有效改善。

模型参考自适应;变参数;异步电机;矢量控制;转速辨识

0 引 言

在异步电机高性能的矢量控制与直接转矩控制算法中，速度传感器几乎是不可少的检测设备。它的使用增加系统成本，降低了可靠性，还限制了在恶劣环境下的运用，因此，无速度传感器技术成为当前研究电机控制的热点[1-2]。

无速度传感器技术的关键性问题是磁链与转速的辨识，磁链与转速的辨识误差直接影响电机的性能。目前，转子磁链观测广泛采用的方法有电压模型法、电流模型法及基于两者的混合模型法。转速辨识方法主要有直接计算法[2]、模型参考自适应法[3-4]、状态观测法[5-6]、转子齿谐波法[7]、高频注入法及神经元网络法等，其中MRAS转速辨识法不仅具有结构简单，且具有转速渐进收敛性。MRAS法速度辨识准确性依赖于参考模型的准确性，因此影响参考模型的参数同样影响转速辨识的精度。在常规的MRAS法中，电压模型法中纯积分器存在直流漂移与积分初始值问题，为了解决此问题，文献[3]及文献[8-9]采用低通滤波器代替纯积分器，由此引起的观测磁链相位延迟与幅值误差，采用参考磁链值或参考励磁电流进行补偿。这种方法虽可解决积分漂移问题，但动态性能较差。常规MRAS法辨识系统存在收敛速度慢、低速时转速辨识误差大的缺点，文献[10-11]采用全阶状态观测器法与文献[12]采用降阶状态观测器法具有辨识速度收敛快和动态性能好的优点，但其结构复杂且不易硬件实现。

针对常规MRAS法中存在的缺陷，本文提出一种变参数的模型参考自适应法。该方法采用改进电压模型法作为参考模型，采用变参数PI调节器代替传统的PI调节器，即在电机控制低速段与高速段分别取不同的PI参数。仿真与实验表明，该方法较好解决积分漂移问题，且控制系统响应速度得到较大提高，尤其是低速时的收敛速度与转速辨识误差得到有效提高。

1 转子磁场定向异步电机矢量控制原理

在异步电机磁场定向的控制中，通常把dq坐标系放到同步旋转磁场上，并使d轴与转子磁场方向重合，即基于转子磁场定向，此时转子磁场q轴分量为零(ψrq=0)。因此，异步电机基于转子磁场定向下的派克方程可表示如下：

电压方程：

(1)

磁链方程：

(2)

转矩方程：

(3)

由式(1)～式(2)可推导得转子磁链与转差式：

(4)

将式(4)代入式(3)可得转矩表达式：

(5)

式中：ψsd,ψsq,ψrd,ψrq为定转子磁链dq轴上分量；Ls,Lr,Lm为定转子电感与定转子间互感；Rs，Rr为定转子电阻；ωr为转子角速度;ωs为定子角频率;ωsl为转差;Tr为转子时间常数；p为微分算子;p为极对数。

由式(4)～式(5)可知，将异步电机模型基于转子磁场后，只须控制定子电流的d轴分量(励磁分量)就可控制转子磁链幅值，当控制转子磁链幅值恒定时，可直接通过控制定子电流的q轴分量(转矩分量)来控制电磁转矩，这样磁链与转矩达到完全解耦的控制，因此，其控制性能几乎可与直流电机相媲美。

2 常规MRAS法的转速辨识方法

常规的模型参考自适应法采用电压模型法作为参考模型，采用αβ静止轴系下的电流模型作为可调模型，其结构如图1所示。

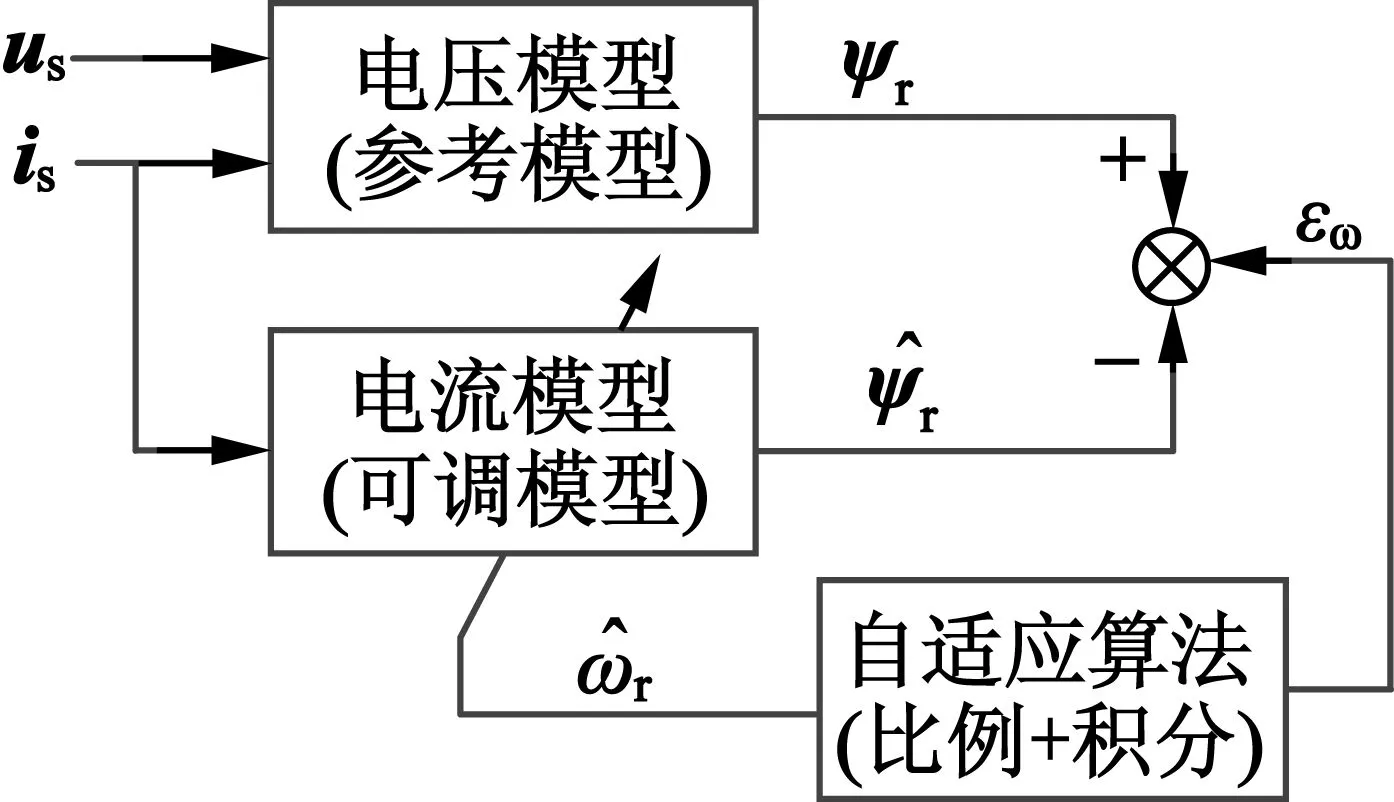
图1 常规MRAS法的基本结构

电压模型法转子磁链观测模型如下：

(6)

可调模型中转子磁链观测器模型：

(7)

如图1所示，这里认为参考模型与电机的实际状态相符，即转子磁链矢量ψr是真实且正确的。 在可调模型中Lm和Tr是不变参数，只有转速ωr是时变参数。采用模型输出的误差产生自适应律来改变辨识转速的值，来达到辨识转速跟踪实际转速的目的。根据Popov超稳定性理，这个系统是渐进收敛的，自适应算法采用PI调节器，如下：

(8)

其中：

(9)

将两模型的磁链误差εω经过合适的PI调节器后得到辨识转速，转速辨识准确性依赖于参考模型的磁链观测的准确性。电压模型法中的积分漂移等问题，以及系统存在收敛速度慢、低速时转速辨识误差大的缺点并没有得到解决，因此需要对其进行改进。

3 变参数MRAS法转速辨识方案

常规MRAS法中电压模型法存在积分漂移问题，文献[3]中纯积分器由低通滤波器代替，而由此引起的观测磁链相位延迟与幅值误差，采用参考磁链值或参考励磁电流进行补偿，结构如图2所示。虽然该方法去掉的纯积分环节解决了积分漂移问题，但是用给定的参考磁链进行补偿时存在动态时(起动过程、突加减负载及弱磁控制)磁链检测发生抖动，致使转速辨识发生波动的问题，且系统存在收敛速度慢、低速时转速辨识误差大的缺点。

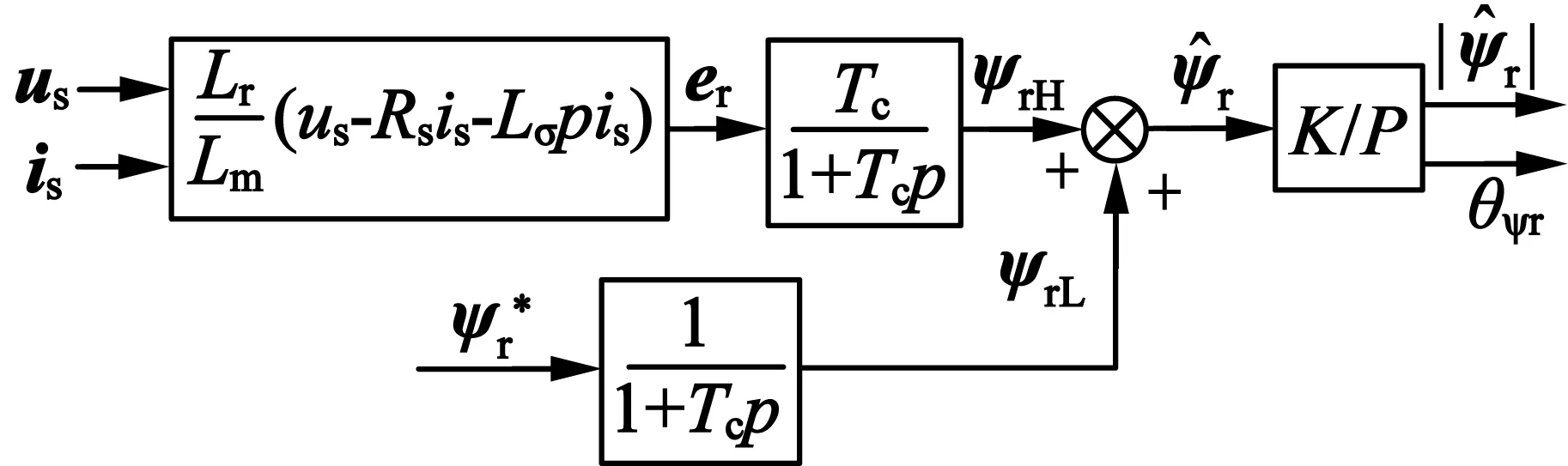
图2 文献[3]中的磁链观测模型

3.1 改进电压模型法的转子磁链观测器原理

为了解决电压模型法中积分漂移问题，本文在文献[3]的基础上进一步改进，得到改进电压模型磁链观测器，将该模型作为MRAS法中参考模型。该方案采用一阶惯性滤波环节来代替纯积分环节，一阶惯性滤波环节是由纯积分器与一阶高通滤波器的有效组合。由此引起的转子观测磁链的幅值与相位误差由实际的励磁电流或者实际的转子磁链进行补偿，可提高系统的动态性能。其详细结构如图3所示。

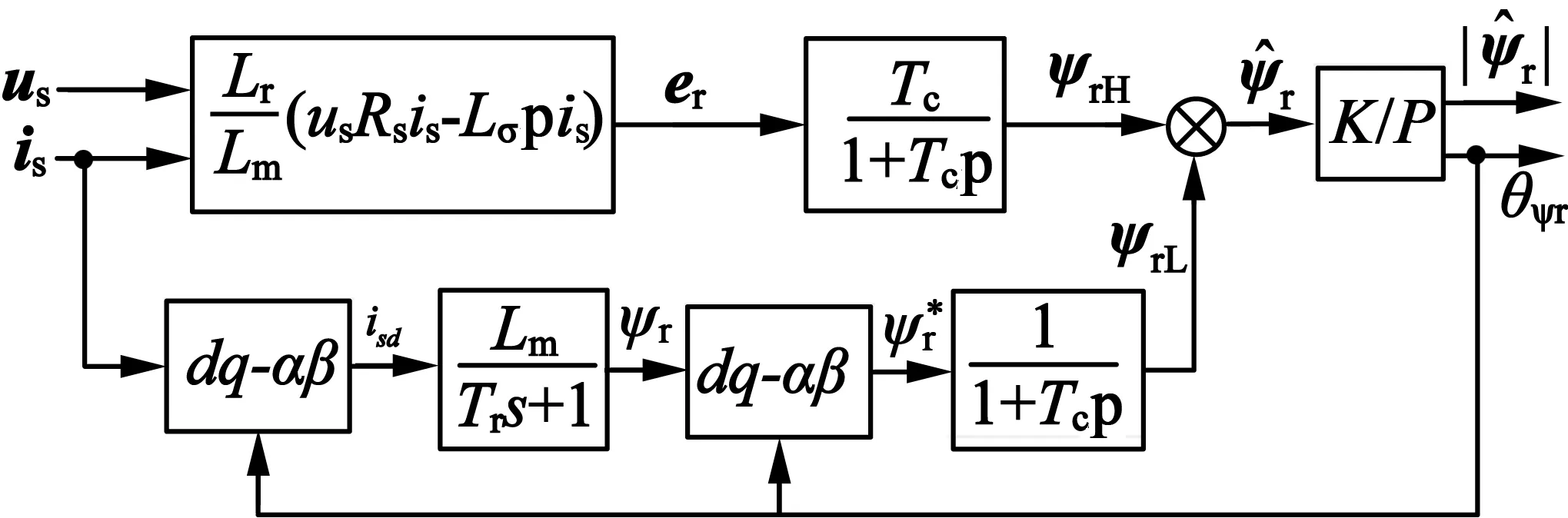
图3 改进电压模型法转子磁链观测器

如图3所示，与图2采用给定磁链参考值补偿不同，该模型在补偿量生成的通道前端加入基于转子磁链定向坐标系中的转子磁链电流模型，即励磁电流isd，用以适应动态时励磁变化的场合。同步旋转dq轴系下的转子磁链电流模型如下：

(10)

转子反电动势计算式：

(11)

转子磁链状态估计ψr的动态方程如下：

(12)

稳态方程：

(13)

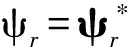
3.2 改进电压模型法的稳定性分析

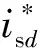
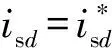
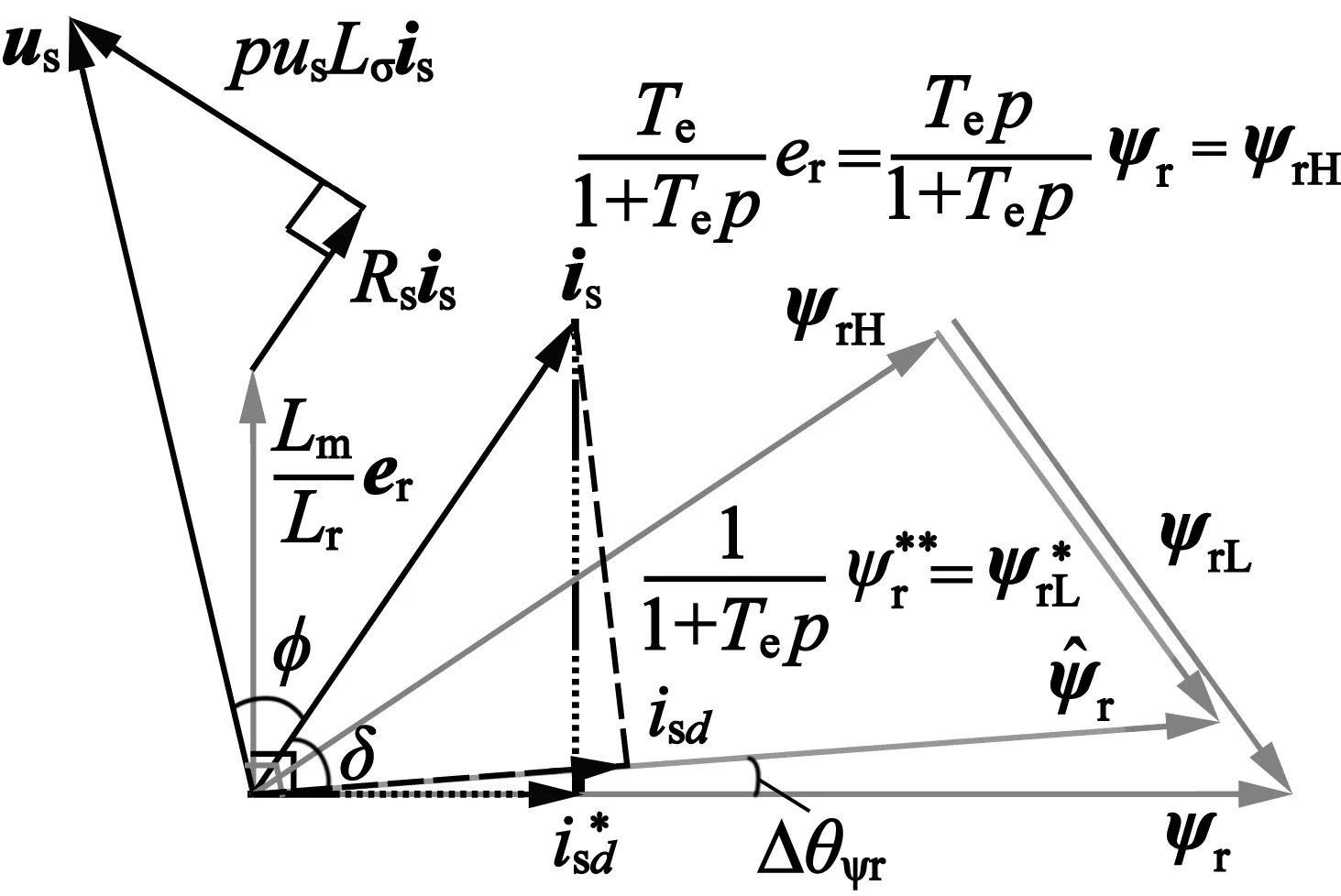
图4 改进电压模型法的空间矢量图

3.3 变参数PI调节器的设计

针对常规的MRAS法中参考模型存在的问题，本文采用改进电压模型法可以较好地解决由纯积分器带来的积分漂移与积分初始值问题。但参考模型在低速时由于定子电阻参数的影响，系统的收敛速度与转速辨识误差较大的缺点，本文可采用变参数PI调节器来解决，可以在低速时适当选择较大的Kp,Ki值，以加速低速时的系统响应速度，减少收敛时间；当转速升高时，可适当选择较小的Kp,Ki值，削弱静差，减小超调，减小稳定时间。因此，在常规MRAS法的基础上，采用变参数模型参考自适应法，Kp,Ki参数的值随着辨识转速值的大小而发生相应的变化。

这里假定ωr<50 rad/s时定义为低速段，此时Kp,Ki为较大的值，当转速超过50 rad/s时，Kp,Ki值按相应比例减小，具体如下：

(14)

(15)

式(14)、式(15)分别为Kp,Ki值的表达式，K0为斜率系数值，可根据设定转速的大小进行调整。其实Kp,Ki可跟根据实际系统的需要预设定不同的转速值，也可以分多段函数进行设定。例如，Kp值可按转速50rad/s为界定，而Ki值可按转速为100rad/s为界定。这就增加了Kp,Ki设定的灵活性。

4 仿真与实验结果分析

在常规MRAS法的基础上进行改进，基于变参数的MRAS法的转速辨识模型如图5所示，参考模型采用改进电压模型法，PI环节采用变参数PI调节器。

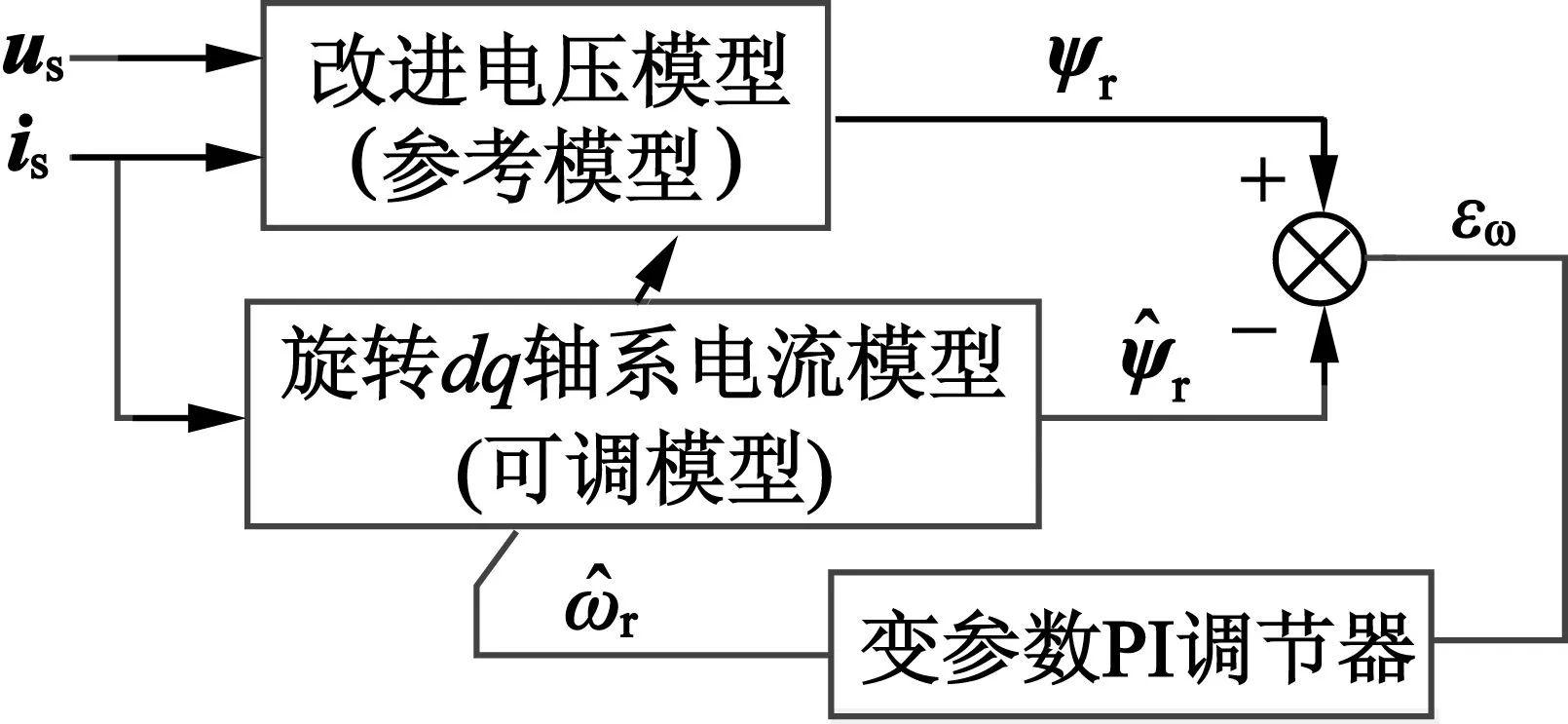
图5 基于变参数MRAS法转速辨识模型

以异步电动机为控制对象，在MATLAB/Simulink建立如图6所示的基于变参数模型参考自适应法的异步电机矢量控制系统仿真模型。仿真参数：Pe=7.5kW，额定电压UN=380V，额定频率f=50Hz，极对数p=2，定子电阻Rs=14.8×10-3Ω，转子电阻Rr=9.3×10-3Ω，定子漏感Lls=0.3×10-3H，转子漏感Llr=0.3×10-3H，互感Lm=10.46×10-3H，转动惯量J=3.1kg·m2，粘滞摩擦系数B=0.08N·m·s，Kp=150，Ki=4 500，K0=10。

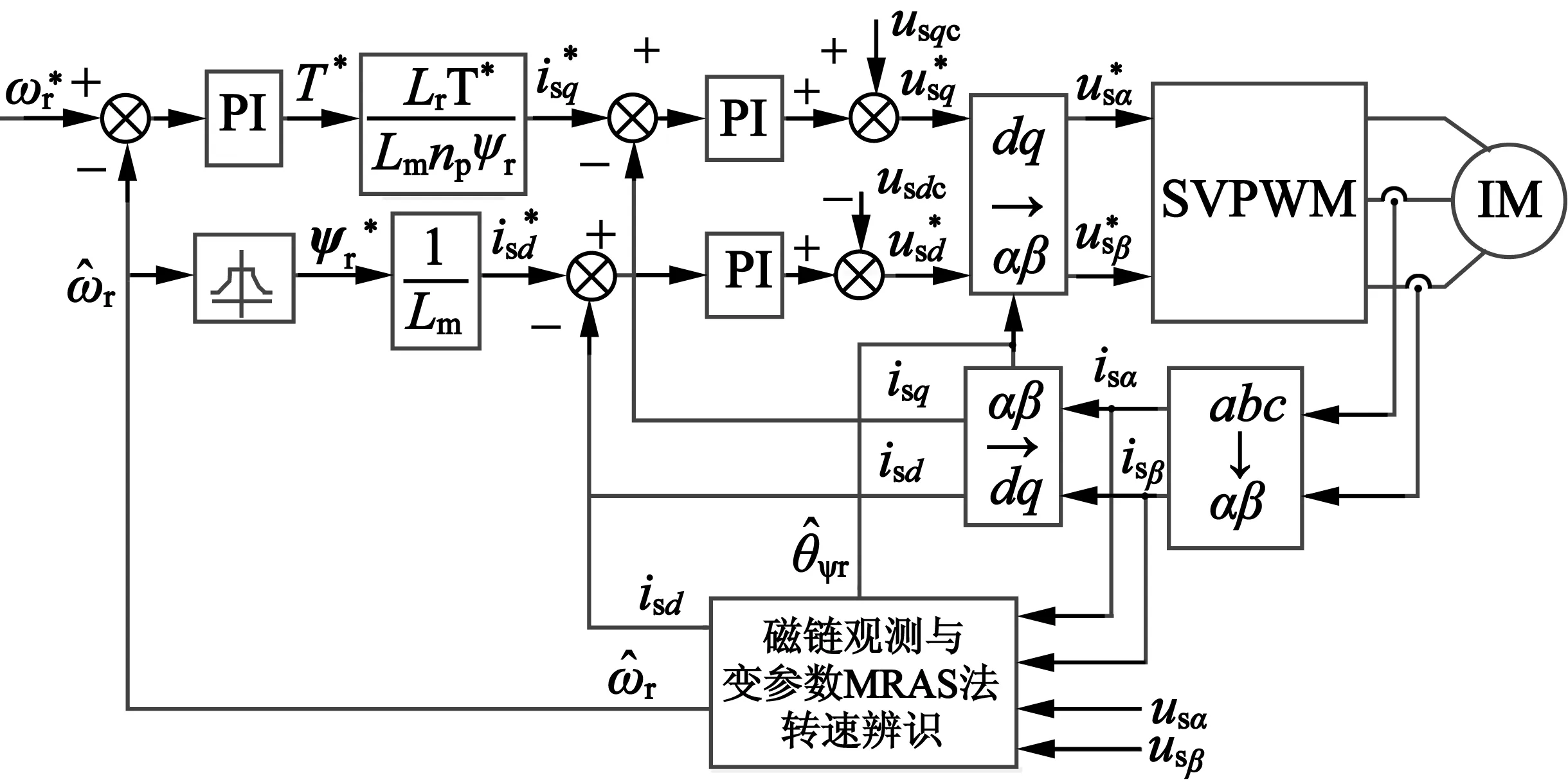
图6 变参数MRAS法的异步电机矢量控制系统设计

为了测试电机转速与转矩发生变化时，变参数MRAS法的动态性能、收敛速度及低转速辨识性能。图7是电机转速由n=0上升到n=400r/min，接着上升到n=1 000r/min，再上升到1 200r/min时的仿真图。图8是转速由n=0上升到n=800r/min，再下降到n=400r/min时的仿真图。由磁链观测图可知，基于改进电压模型法的转子磁链观测值与实际值之间的误差非常小。由转速辨识及误差图可知，变参数MRAS法转速辨识比常规MRAS法减小了超调量、加快了收敛速度、减小了辨识误差及具有低速时转速辨识准确等优点。由电磁转矩及Kp,Ki值变化曲线可知，在低速时(ωr<50rad/s)，Kp,Ki值保持初始值不变，随着转速的上升，其值按相应的比例减小，最终当转速稳定时其值也稳定。实际转矩能够较好地跟踪给定转速，电机控制性能较好。

对上述基于变参数MRAS法的异步电机矢量控制系统方案，采用TI公司的DSP芯片TMS320F2812搭建了该系统，实验所用的感应电机参数如下：电机功率Pn=15kW，额定电压Un=380V，定子阻值Rs=0.121Ω，转子阻值Rr=0.067Ω，定子电感Ls=0.027 82H，转子电感Lr=0.027 46H，定转子互感Lm=0.026 25H，极对数p=6。

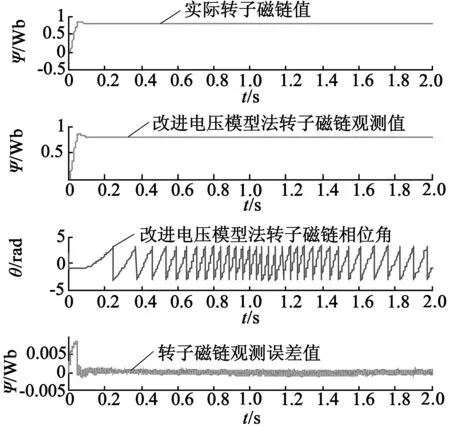
(a)磁链观测

(b)转速辨识

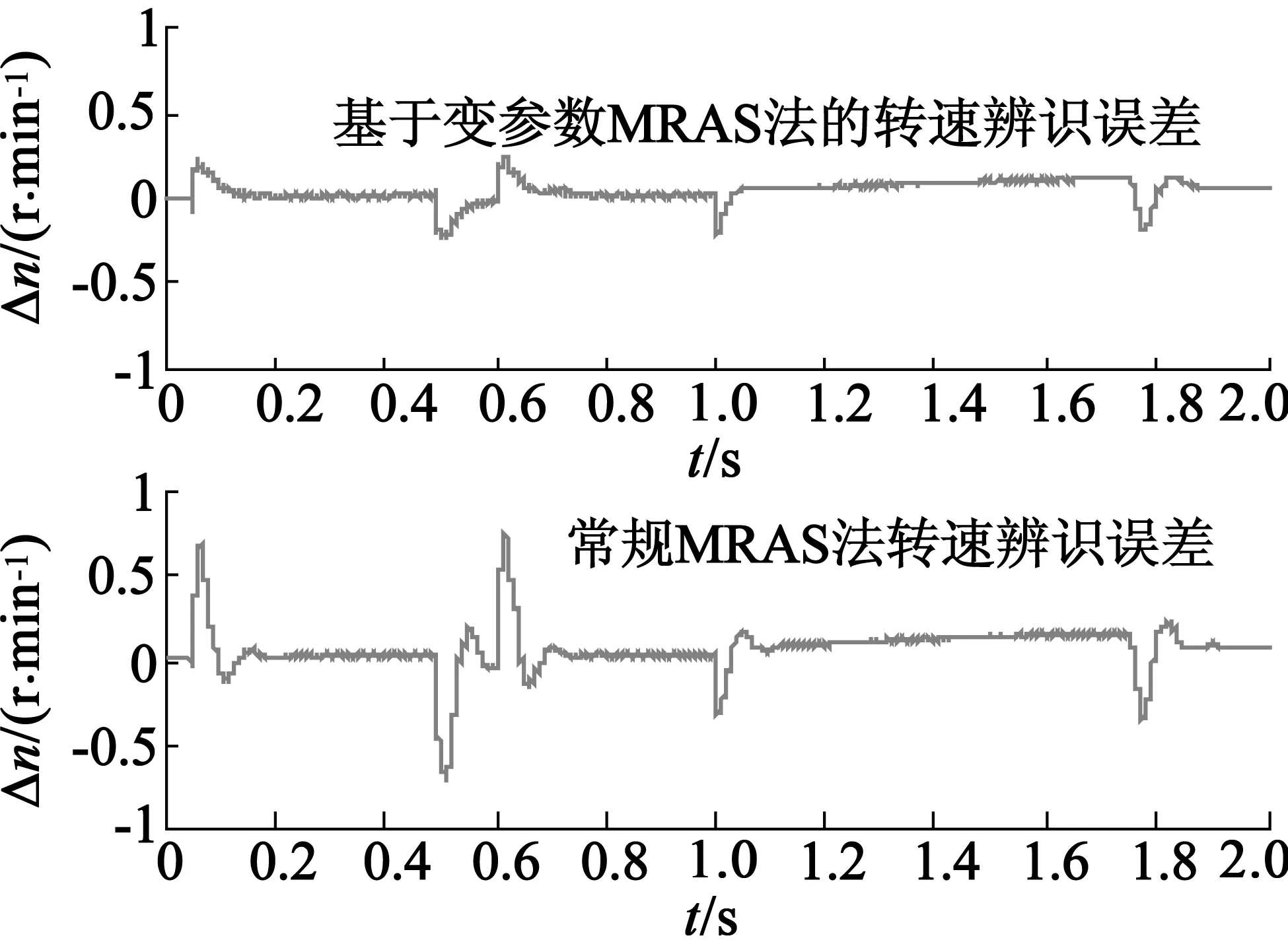
(c)转速辨识误差

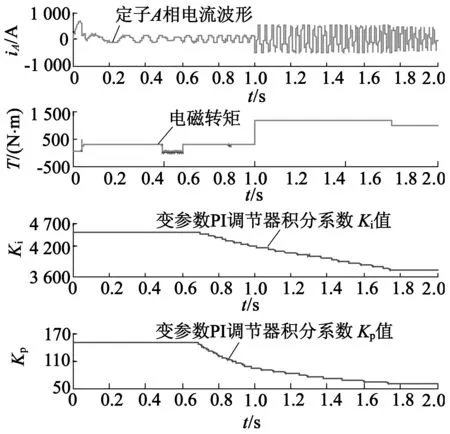
(d)电磁转矩与Ki,Kp值

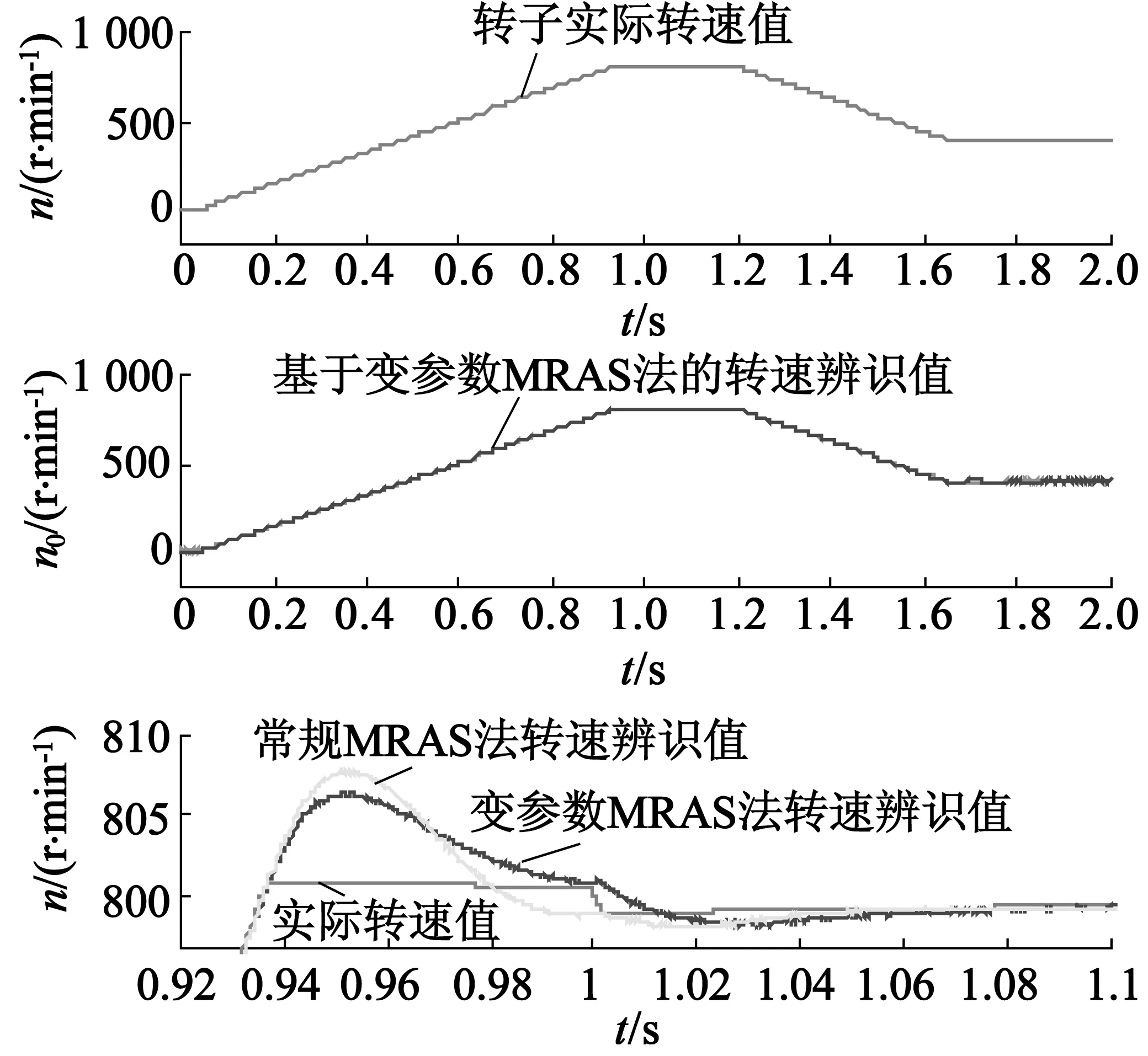
(a)转速辨识

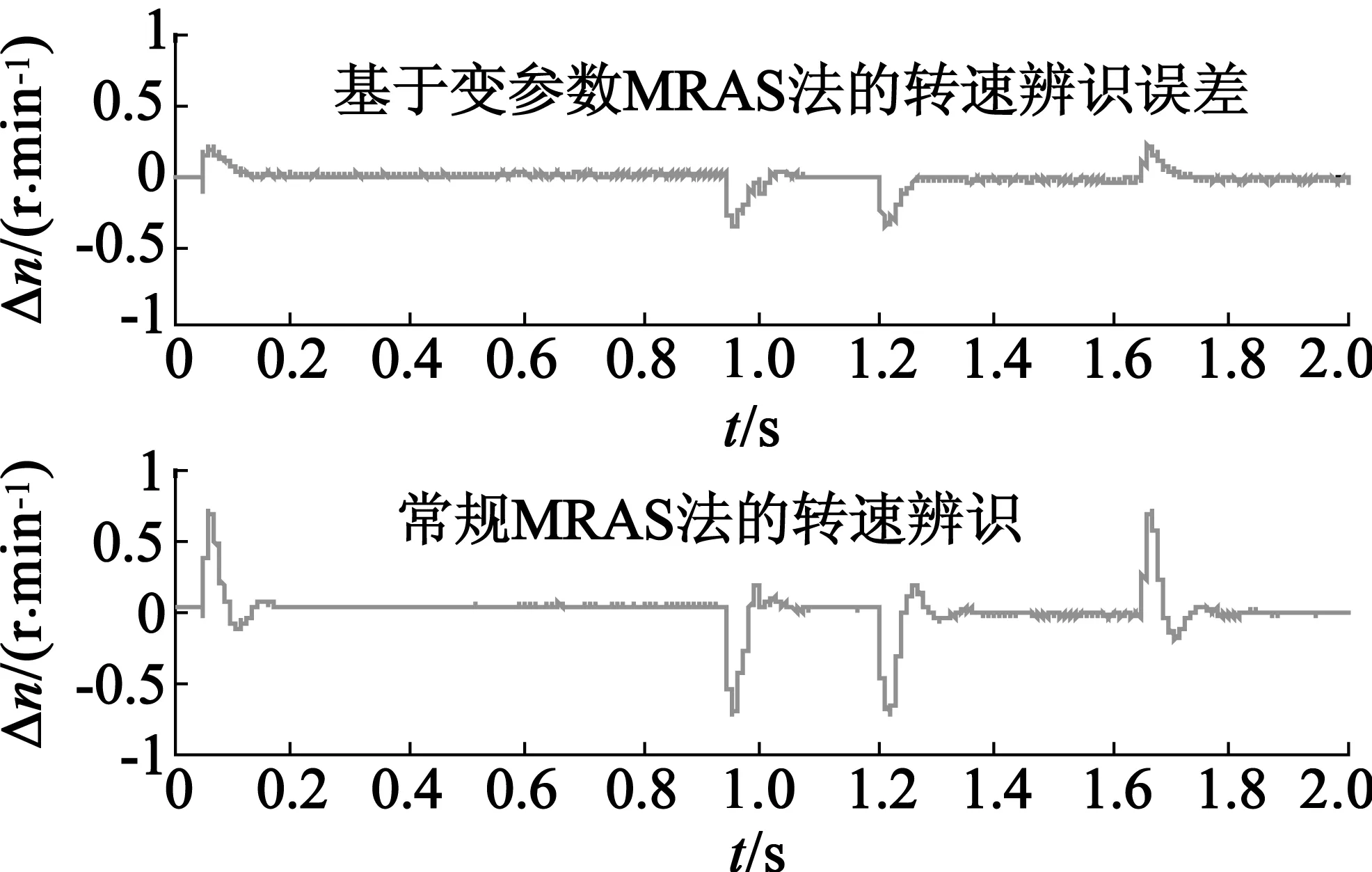
(b)转速辨识误差

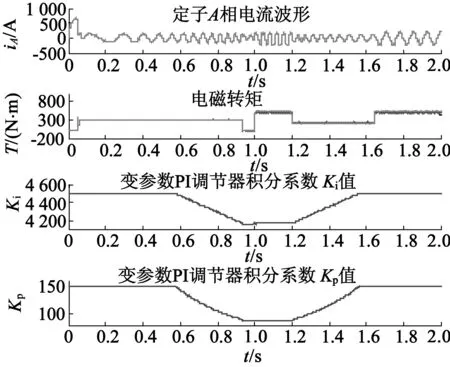
(c)电磁转矩与Ki,Kp值

实验结果：图9是在CCS上得到的SVPWM波形，图10是CCS上得到的给定转速与辨识转速波形。通过实验波形分析可知，转速辨识误差在允许的范围内，可见变参数MRAS法可较好地运用在工程实践中。

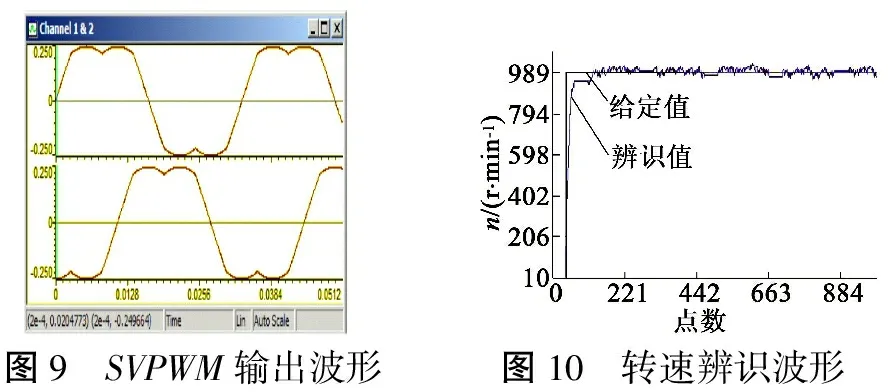
图9 SVPWM输出波形图10 转速辨识波形

5 结 语

本文在常规MRAS法的基础上，采用改进电压模型法磁链观测器作为参考模型，且为了解决系统的响应速度及低速时转速辨识误差较大的缺点，采用分段变参数PI调节器来代替传统PI调节器，仿真与实验表明，改进电压模型法磁链观测克服了积分漂移及低速检测波动大的问题，变参数MRAS法转速辨识比常规MRAS法减小了超调量、加快了收敛速度、减小了辨识误差及低速时转速辨识准确等优点。通过实验表明，变参数MRAS法可以较好地运用在转速经常变化的场合，其具有较好的工程实用价值。

[1] 宋文祥，周杰.感应电机磁链观测及矢量控制低速发电运行控制方法综述[J].电机与控制应用，2013，40(11)：1-7.

[2] 王成元，夏加宽，孙宜标.现代电机控制技术[M].北京：机械工业出版社，2012.

[3] 周亚丽,李永东,郑泽东.基于MRAS的感应电机无速度传感器矢量控制[J].电气传动,2009,39(4)：3-8.

[4]YANGG,CHINTH.Adaptive-speedidentificationschemeforaninverterinductionmotordrive[J].IEEETrans.onIndustryElectronics,1993,29(4):820-825.

[5]JABBOURZ,MOREAUS,RIWANA.Speedestimationimprovementusingfullorderstateobserverforahapticinterface[J].IEEETrans.onIndustrialElectronics,2009:1482-1487.

[6] 郑泽东，李永东，王琛琛.异步电机全阶自适应磁链观测和速度辨识研究[J].电气传动，2006，36(7)：7-10.

[7]HURSTKD,HABETLERTG,etal.Speedsensorlessfield-orientedcontrolofinductionmachinesusingcurrentharmonicspectralestimation[C]//IEEEAnnualMeetingofIndustryApplicationSociety，1994:601-607.

[8] 李永东.交流电机数字控制系统[M].北京:机械工业出版社, 2002.

[9] 齐桓若，刘其辉.基于一种新型转子磁链观测方法的矢量控制高压变频器[J].电机与控制应用，2014,41(10)：61-67.

[10] 李瑞强，刘跃敏，范波.一种改善的全阶磁链观测器及速度计算[J].微电机，2013,46(2)：50-54.

[11] 柳巍，阮毅，吴晓新，等.基于伪降阶磁链观测器的速度辨识方法[J].电机与控制应用，2014,41(8)：13-17.

[12] 宋文祥,周杰，阮智勇，等.无速度传感器感应电机降阶磁链观测器方法及实现[J].电机与控制学报，2013,17(6):42-50.

Induction Motor Vector Control System Based on Variable Parameters MRAS

HUANG Shao-gang,SONG Feng-lin,HONG Jian-feng,CHEN Jian-qiang

(Nanchang University,Nanchang 330031,China)

A variable parameter of MRAS method was proposed, which used improved voltage method flux observer model as the reference model,and used variable parameters PI controller instead of the traditional PI regulator, that is to use different PI parameters when at low speed and high speed sections, whose value decreases as the speed changes.The simulation and experiments of induction motor speed sensorless vector control system based on the variable parameters MRAS method show that the improved voltage method can better solve integration drift problem, and the control system response speed is greatly improved, especially at low speed section convergence and identification error effectively improved.

model reference adaptive; variable parameter； induction motor; vector control; speed identification

张刚(1987-)，男，硕士，讲师，研究方向为新型电机控制技术、智能建筑电气设计。

2015-01-08

国家自然科学基金项目(51467011)；江西省研究生创新资金项目(YC2013-S059)

TM343

A

1004-7018(2016)02-0062-05