多阈值提取平面点云边界点的方法
2016-07-19廖中平刘科向雨蔡晨光
廖中平 刘科 向雨 蔡晨光

摘要:针对基于切片技术的点云数据重建算法需要提取切片内点云边界点,及现有算法效率低、提取效果不好等问题,提出一种多阈值提取平面点云边界点的算法。通过选取判断点的k个近邻点,计算相邻两点与判断点连线间夹角,由于边界点必存在最大夹角,通过判断最大夹角是否超过设定阈值,从而快速提取边界点。通过对阈值设值分析,不同点云数据的边界提取实验及几种方法间比较,该方法不受点云形状影响,均能较好提取边界点,且优于其他3种算法。结果表明该方法在保证原始点云特征信息的前提下,可较好提取边界点,提高后续点云重建速度与效率。
关键词:
点云;边界点;阈值;效率;点云形状
中图分类号: P232; TP391.41 文献标志码:A
0引言
三维激光扫描技术能快速获取扫描对象表面的大量点云数据,基于点云数据对物体进行三维重建,已成为当前逆向工程三维重构领域中的研究热点[1-2]。采用切片技术的点云重建方法可将原始无序的三维点云数据转化为具有层次结构、有序组织形式的数据,使得对物体的重建更加有效。切片技术就是用一组平行平面沿着某一给定方向、给定间隔对三维点云进行划分,再将平面两侧的点云投影到平面上,从而将三维点云转换为二维点集,在此基础上再进行物体表面重建[3-4],因此,如何提取投影在平面上点云的边界点,成为后续物体表面三维重构的重要一步。
文献[5]中,在提取平面边界点时提出以判断点为中心,将其邻域采用不同的分割方法分成若干区域,再根据某一区域内是否有散乱点作为判断准则来提取边界点。由于每进行一次判断,需要将其他散乱点遍历一次,导致运算速度慢,效率低。文献[6]中,将判断点的邻域从4个均匀区域增至8个均匀的区域,提取效果有所改善,仍不能较好提取凹陷区域边界点。文献[7]在提取三维边界散乱点云时,采用R*tree对点云数据进行动态聚类划分,依据k近邻点以最小二乘法拟合该点集的切平面,将k个点投影在切平面上,再以点云中最大夹角与设定的阈值为依据来提取边界点;但文中未对阈值大小的设置进行分析,也未考虑平面上点云形状对提取效果的影响。文献[8]中,通过计算判断点周边点之间的夹角,采用角度标准差作为边界点判断依据来提取三维点云边界点;但该方法对离散、分布不均匀的点云提取效果不理想。文献[9]中,在提取保留三维边界点时,将近邻点投影到某一平面上,然后选取若干参考面,统计位于参考面两侧的点数,以两侧点数之差作为判断的标准;但该方法不适合平面点云边界点的提取。文献[10]中,采用矢量合成的思想,将判断点周围点构成矢量并单位化后进行叠加,依据叠加后的矢量的模与矢量数量的比值作为判断准则;但该算法对非均匀分布的点云及凹陷处的边界点提取效果不理想。
以上一些算法在提取三维边界点时,效果较好;但经实验将其计算思想应用在提取二维平面散乱点的边界点时,则提取效果不理想,尤其是有凹陷的点云形状边界的提取。同时计算过程复杂、繁琐,如文献[5]需要进行区域划分。本文在文献[7]基础上进行改进,提出一种基于多阈值的提取平面点云边界点算法,不需对近邻点进行区域划分。同时对本方法中阈值的设定进行了分析,实验结果表明,依据本文的阈值设置原则,使用本文方法能够较好地提取边界点。
1多阈值提取平面点云边界点的方法
1.1近邻点的检索
二维平面散乱点云没有明显的几何分布特征,点与点之间也没有拓扑关系,因此当点云数量巨大,寻找k近邻点时,有必要建立点云间的拓扑关系,提高搜索速度。常用方法有栅格法、八叉树法、空间单元格法和KDtree法等[11]。由于切片面上点云数据量较小,且为二维点云数据,因此采用简单的栅格法建立点间的拓扑关系,提高k近邻点搜索速度。栅格大小的设置与点云密度有关,如果设置不当,会影响计算效率[11]。
点云密度ρ的估算方法如下所示。
在点云中随机抽取n个点,对每个点gi(i=1,2,…,n)在点云中搜索距其距离最近的m个点,并计算每点到其距离Di,求其平均值即为点云密度估计值:
ρ=(∑ni=1∑mj=1Dji)/(n×m)(1)
依此密度值设置栅格尺寸,在获取得到近邻点后,可依据距离对近邻点排序,获得最近的k个近邻点[12]。
1.2点集的几何特性分析
判断点P的近邻点分布,若近邻点偏向一侧,则认为P点为边界点;反之若近邻点均匀分布在其四周,该点则为内部点。P点为内部点和外部点的点集分布如图1所示。
边界点具有不确定性,即边界点是否处在边界线上,是不确定的,如图2所示,因此,不能提取出完全与边界一致的点,而只能提取出其近似边界点,但要在最大限度上保留其边界特征[5]。
1.3判断过程
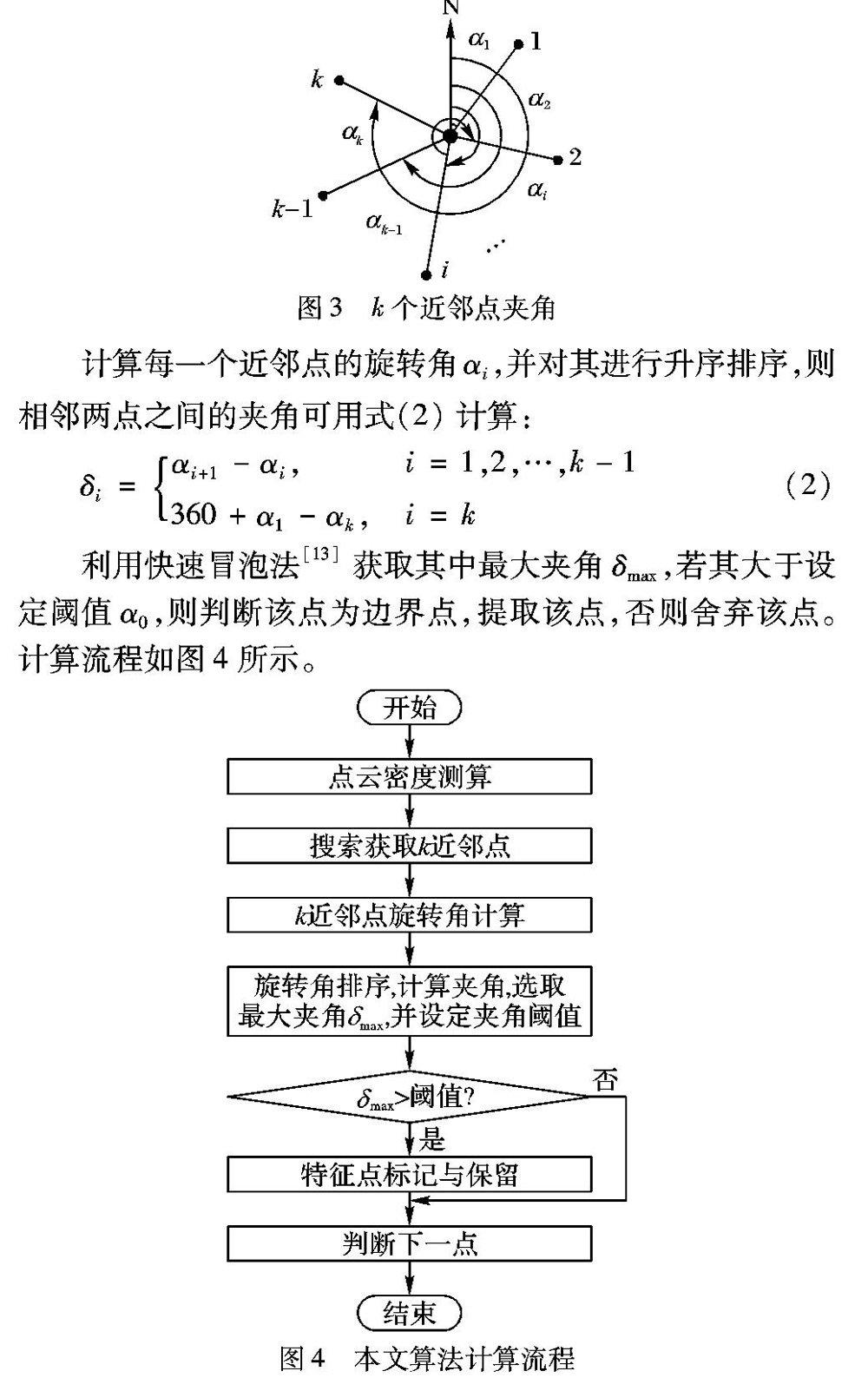
依据预测点云密度ρ设置栅格尺寸,获取k个近邻点。以当前判断点P为中心,分别连接各个近邻点,以选定的某一方向为起始方向,顺时针旋转到近邻点所在的线上,得到k个与之对应的旋转角,如图3所示。
2实验及分析
2.1实验说明
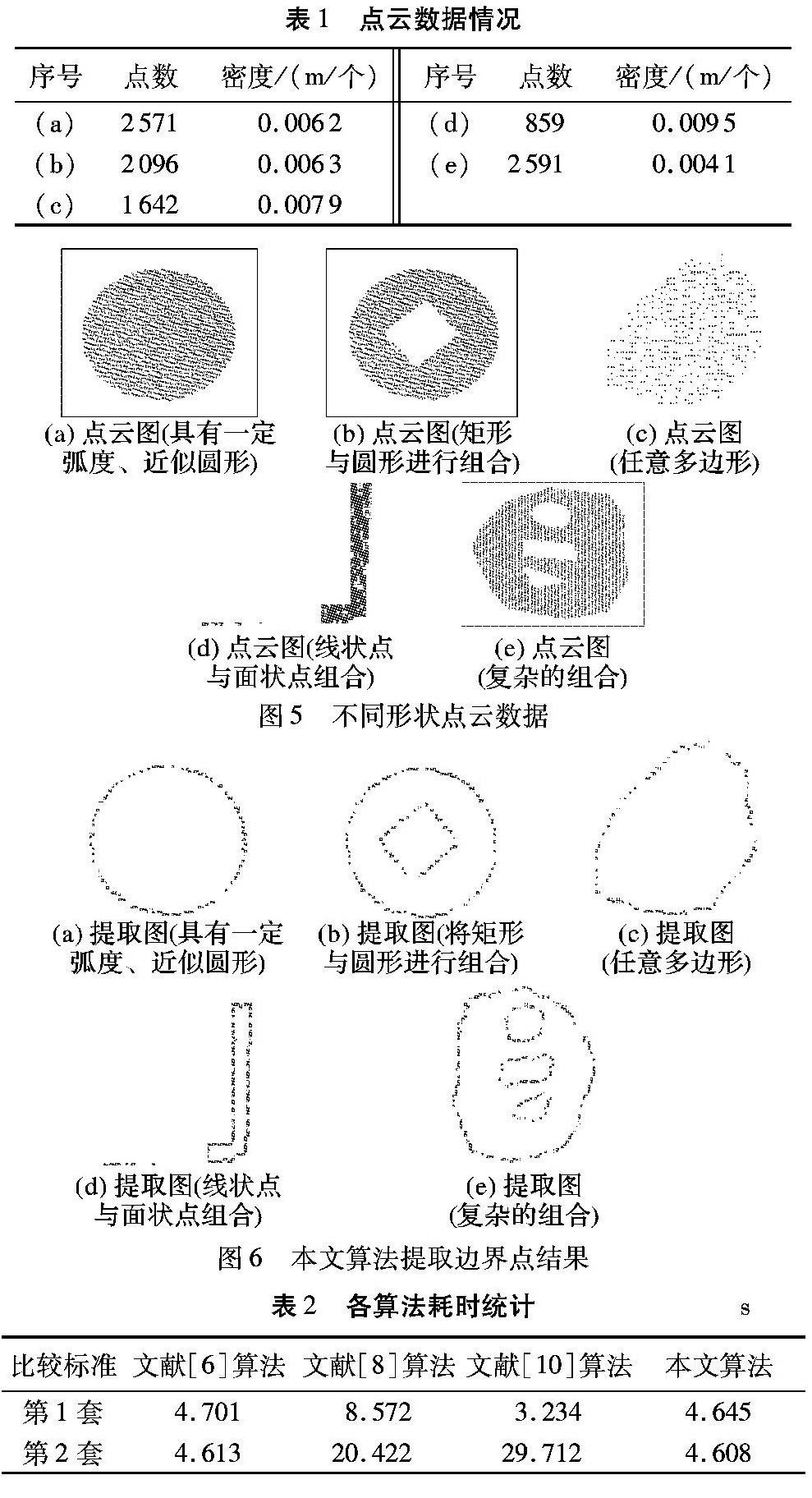
本文使用Leica C10三维激光扫描仪采集数据,选取5类点云数据,分布情况如图5所示。其中:图5(a)对应具有一定弧度、近似圆形的点云数据;图5(b)中则将矩形与圆形进行组合;图5(c)为任意多边形点云数据;图5(d)为线状点与面状点组合;图5(e)中则是更加复杂的组合。其中各点云的点数及密度情况如表1所示。同时增加了文献[6]、[8]、[10]对应方法与本文方法的比较。由于各算法效率与获得邻近点方法及邻近点数量有关,因此采用两套标准比较:第1套标准中,各方法获取邻近点方法与数量相同的前提下比较,不考虑最终提取效果;第2套是在最大限度提取边界点前提下比较,统计各种算法耗时。
2.2实验结果
算法是在PC机配置为AMD E350 Processor 1.60GHz,内存为3.0GB,Windows 7 32位系统上运行,使用Matlab 7.0进行编程,冒泡法进行排序,使用本文方法分别对图5中的点云数据进行边界点的提取,均采用k=15、α0=120°的阈值,其提取的边界点效果如图6所示。表2为4种算法在第1两套标准下耗时统计结果,图7中的(a)~(d)则为4种算法在第2套标准下的提取结果。其中:图7(a)为文献[6]算法提取结果,图7(b)为文献[8]算法提取结果,图7(c)为文献[10]算法提取结果,图7(d)为本文的提取结果。
2.3实验结果分析
由表2中的4种算法耗时可知,由于第1套标准未考虑提取效果,因此4种算法在第1种标准下耗时均少于在第2套标准下的耗时。由图7(a)~(d)可知,本文算法与文献[6]对应的算法提取效果最好;但本文算法在提取内部边界点上要优于文献[6]算法。
在第1套标准下,4种算法均需计算获取邻近点。但文献[10]矢量合成算法,只需计算矢量并求和,计算过程相比其余3种算法计算相邻点间夹角要简单;同时也少了计算邻点与指定方向的夹角这一步骤,因此在不考虑提取效果的前提下效率最高;同时计算过程所占存储空间最小。而文献[8]角度方差法由于计算角度方差相对于夹角计算要复杂,因此效率最低。而文献[6]区域划分法由于增加对点距离限制条件,因此效率次于本文算法,运行内存也高于本文算法。而在第2套标准下,由于各算法中参数大小的改变,导致最后提取耗时相差较大;但本文算法效率依旧高于其余3种。
由图6可知,在使用相同的阈值k、α0进行边界点提取,均能提取点云边界点。其中图6(a)~(d)提取效果相对于图6(e)较好,图6(e)中内部边界点遗漏较多。结果表明在点云密度ρ、阈值k、α0大致相同的情况下,提取效果与点云形状有关。
平面多边形可分为凸多边形和凹多边形,对于带有弧段的多边形,可以认为其是无穷多边形。对于凸多边形,其定义为:设pi=(xi,yi)((xi,yi)∈R2(i=1,2,…,n,且pn+1=p1))是构成多边形的n个顶点,若线段pi-1pi与pipi+1所形成的内角(即该多边形围成的有界区域内所形成的角)不大于180°,则称点pi为凸点,否则称为凹点;若n个顶点都是凸点,则称该多边形为凸多边形(n≥4),用O表示[14]。其具有所有内角均是劣角、外角均是优角的性质,因此对于凸多边形的点云提取边界点时,由于内部点四周较均匀分布着离散点,因此设置夹角阈值α0要接近但要小于180°,则可较好保留边界点。如果大于或非常接近180°,则会将位于直线上的边界点忽略掉,只能提取出拐点处的边界点,效果不好。
对于凹多边形,由于不具有凸多边形的外角均为优角的性质,因此在设置阈值时,需要依据点云形状来具体设置。凹、凸多边形的点云形状如图8所示,黑色部分为散乱点云分布情况。在凹多边形中,有两个外角β1、 β2,均是劣角。如果仍是选择角度阈值接近180°,当取一定数量近邻点时,相邻点间夹角就会均会小于180°,则会将β1、 β2顶点处的边界点给忽略掉,因此需重新设置角度阈值。针对此种情况,本文处理方法是统计多边形中凹角中劣角的个数,然后估计劣角的角度大小范围,在此基础上设置角度阈值,使其接近外角中最小的角度,该图中β1较小,则设置的阈值应接近β1。
2.3.1凹、凸多边形点云提取实验
本次实验选取的数据是表1中(e)中所对应的数据,此点云形状中,外轮廓边界点云对应凸多边形,内部轮廓对应凹多边形。根据点云所构成的形状来看,内部轮廓中凹角中最小角度大致为45°,因此本次选取角度阈值α0=45°、60°、120°、150°、180°。同时为了研究k大小对角度设置的影响,选取了k=5,15,25进行组合实验。其中在α0=45°时,在原有的k值基础上,增加了k=30,35,40,50四组实验。其阈值与序号对应关系如表3所示,表3与图9存在重复表达的现象,故删除表3。提取效果如图9所示。
2.3.2结果分析
图9中的19种提取结果进一步验证了2.3节中阈值设置原则的可行性,对于该点云外轮廓的提取,由于外轮廓边界点所构成的形状为凸多边形,因此在k不断变化时,只要α0值不是很接近或大于180°,则外轮廓边界点就会较好地保留;而如果大于180°,则会将位于一条直线上的边界点给忽略掉,而只保留凸角处的边界点。图9中的(d)、(i)、(n),拐角处边界点保留较好,位于直线上的边界点则遗漏较多。对于内边界点的提取,则角度阈值α0接近或等于45°时提取效果比较好。α0为120°、150°和180°的内部边界点遗漏严重,甚至没有达到提取效果。如需两者兼顾,同时提取外轮廓与内边界点,则需将k值增大,α0接近凹角最小角范围,图9(g)与图9(l)提取效果的差别在于前者k值小于后者。同时在提取实验过程中发现,α0越接近凹角最小值,则k值需相应增加,才能提取出理想的边界效果。由图4的本文算法计算流程可知,k值的大小直接决定着程序的运算量,因此在提取过程中,在保证边界信息准确的前提下,避免设置α0过小,k值过大组合的情况。如图9(k)、(p)要达到图9(q)的提取效果,k值由25,30增加到35,无形中增加计算量。图9(i)相对图9(q),较好地保留了边界点;但计算量相对于图9(k)没有增加。同时并非k值越大,提取的效果会越好;相反有时会降低效率。图9(r)、(s)相对图9(q)虽k值增加,提取效果并没提高;但计算量却增加不少。
3结语
本文提出的基于多阈值提取二维平面点云边界点的算法,依据最近邻点阈值k与相邻点夹角阈值α0对平面点云进行边界点提取,并对两个阈值的设置进行分析,也给出了凹凸多边形的阈值设置原则。这可应用于以后对不同情况提取边界点和后续基于切片技术的点云数据重建。由于本文未对不同点云密度的情况进行研究,而点云密度可能影响到本文算法阈值的设置,因此在接下来的工作中会研究点云密度对阈值的影响,使该算法适用性更广。
参考文献:
[1]
程效军,方芳.基于形态学的散乱点云轮廓特征线提取[J].同济大学学报(自然科学版),2014,42(11):1738-1743.(CHENG X J, FANG F. Morphologybased scatter point cloud contour extraction [J]. Journal of Tongji University (Natural Science), 2014, 42(11): 1738-1743.)
[2]
徐工,程效军.基于小波技术的散乱点云自适应压缩算法[J].同济大学学报(自然科学版),2013,41(11):1738-1743.(XU G, CHENG X J. Adaptive reduction algorithm of scattered point clouds based on wavelet technology [J]. Journal of Tongji University (Natural Science), 2013, 41(11): 1738-1743.)
[3]
柯映林,王青.反求工程中的点云切片算法研究[J].计算机辅助设计与图形学学报,2005,17(8):1798-1802.(KE Y L, WANG Q. Research on point cloud slicing technology in reverse engineering [J]. Journal of Computer Aided Design & Computer Graphics, 2005, 17(8): 1798-1802.)
[4]
WU Y F, WONG Y S, LOH H T, et al. Modeling cloud data using an adaptive slicing approach [J]. ComputerAided Design, 2004, 36(3): 231-240.
[5]
邱泽阳,宋晓宇,张树生,等.一种新的散乱数据边界点提取方法[J].机械科学与技术,2004,23(9):1037-1039.(QIU Z Y, SONG X Y, ZHANG S S, et al. A new method for the extraction of boundary points from scatter data points [J]. Mechanical Science and Technology, 2004, 23(9): 1037-1039.)
[6]
齐维毅,丁言镁,吴丽娟.四边形网格划分过程中的边界其提取与优化算法实现[J].小型微型计算机系统,2007,28(10):1861-1864.(QI W Y, DING Y M, WU L J. Realization of the edge points searching and edges optimization in quadrangular mesh generation process [J]. Journal of Chinese Computer Systems, 2007, 28(10): 1861-1864.)
[7]
孙殿柱,范志先,李延瑞.散乱数据点云边界特征自动提取算法[J].华中科技大学学报(自然科学版),2008,36(8):82-84.(SUN D Z, FAN Z X, LI Y R. Automatic extraction of boundary characteristic from scatter data [J]. Journal of Huazhong University of Science and Technology (Nature Science), 2008, 36(8): 82-84.)
[8]
刘章明,董慧颖,王金涛.一种非封闭自由曲面的点云边界提取算法[J].计算机应用,2009,29(Z2):247-249.(LIU Z M, DONG H Y, WANG J T. Boundary extraction algorithm of point clouds on nonclosed freeform surface [J]. Journal of Computer Applications, 2009, 29(Z2): 247-249.)
[9]
黄文明,肖朝霞,温佩芝,等.保留边界的点云简化方法[J].计算机应用,2010,30(2):348-350.(HUANG W M, XIAO Z X, WEN P Z, et al. Point cloud simplification with boundary points reservation [J]. Journal of Computer Applications, 2010, 30(2): 348-350.)
[10]
陈义仁,王一宾,彭张节,等.一种改进的散乱点云边界特征点提取算法[J].计算机工程与应用,2012,48(23):177-181.(CHEN Y R, WANG Y B, PENG Z J, et al. Improved algorithm for extraction of boundary characteristic point from scattered point cloud [J]. Computer Engineering and Applications, 2012, 48(23): 177-181.)
[11]
吴禄慎,晏海平,陈华伟,等.一种基于散乱点云的边界提取算法[J].计算机应用与软件,2014,31(11):264-268.(WU L S, YAN H P, CHEN H W, et al. A boundary extraction algorithm based on scattered point cloud [J]. Computer Applications and Software, 2014, 31(11): 264-268.)
[12]
杨振清,雍永磊.基于点云切片的边界提取[J].计算机应用与软件,2014,31(1):221-224.(YANG Z Q, YONG Y L. Boundary extraction based on point cloud slices [J]. Computer Applications and Software, 2014, 31(1): 221-224.)
[13]
龚沛曾,杨志强,陆慰民.Visual Basic程序设计教程[M].3版.北京:高等教育出版社,2007:106-107.(GONG P Z, YANG Z Q, LU W M. An Introduction to Visual Basic Programming [M]. 3rd ed.Beijing: Higher Education Press, 2007: 106-107.)
[14]
戴光明,王茂才,彭雷.凸多边形最小面积四边形包围盒算法[J].华中科技大学学报(自然科学版),2006,34(6):71-73.(DAI G M, WANG M C, PENG L. Algorithm for smallest quadrangle encasing box of convex polygon [J]. Journal of Huazhong University of Science and Technology (Nature Science), 2006, 34(6): 71-73.)
