一种改进的稀疏度自适应压缩采样匹配追踪算法*
2016-11-30倪加明孙钦者陆家明
倪加明,孙钦者,陆家明
(杭州电子科技大学 通信工程学院,浙江 杭州 310018)
一种改进的稀疏度自适应压缩采样匹配追踪算法*
倪加明,孙钦者,陆家明
(杭州电子科技大学 通信工程学院,浙江 杭州 310018)
针对未知稀疏度信号的重建,提出了一种改进的稀疏度自适应压缩采样匹配追踪(MACSMP)算法。该算法以压缩采样匹配追踪(CoSaMP)算法为基础,结合变步长自适应的思想,摆脱了对于信号稀疏度的依赖,并在迭代过程中引入正则化思想,从而提升了算法的重构精度。仿真结果表明,文中提出的MACSMP算法在重构性能与运行效率两方面都要优于SAMP、OMP、CoSaMP这几种算法,且其计算量较低,运行时间较短。
压缩感知;重构算法;稀疏度自适应;正则化
0 引 言
传统采样定理中要求采样频率需大于信号带宽的两倍,以保证恢复出来的信号不失真,因而我们在用它处理宽频段类信号时就存在很多困难。压缩感知(Compressed Sensing,CS)[1]理论的提出成功解决了这一难题,其能够以远低于Nyquist率的采样频率对信号采样,且可以使用相关重构算法来恢复信号。
重构算法是压缩感知领域一个重要的研究方向,为此相关学者在这一方面做了很多功课,先后提出了许多性能比较优异的算法。在这些算法中,贪婪算法由于自身结构较为简单且运算量相对较少,故而得到了广泛应用。典型的有正交匹配追踪算法(Orthogonal Matching Pursuit,OMP)[2]、正则化正交匹配追踪算法(Regularization Orthogonal Matching Pursuit,ROMP)[3]、压缩采样匹配追踪算法(Compressive Sampling Matching Pursuit,CoSaMP)以及稀疏度自适应匹配追踪算法(Sparsity Adaptive Matching Pursuit,SAMP)[4]。本文在研究上述几种典型重建算法的基础上,将CoSaMP算法结合自适应的思想以及正则化的方法并加以改进,提出了一种改进的自适应压缩采样匹配追踪(MACSMP)算法。
1 压缩感知与重构算法
压缩感知理论表明,若信号是稀疏的或是可压缩的,则可用测量矩阵对信号进行观测,以少量的观测值来表示原信号,然后利用重建算法恢复原信号。
假设离散信号x(x∈RN)是N×1维列矢量,在经过一组N×1维向量基等效表示后,其中非零值系数只有K( K≪N)个,或者是大系数只有K个且其他系数均较小。那么,我们就可以将其在该变换域内看作是稀疏的,用数学公式可表示为:

式中,α=[α1,…,αN]T是稀疏矢量,ψ=[ψ1,…,ψN]是稀疏字典,K是稀疏度。
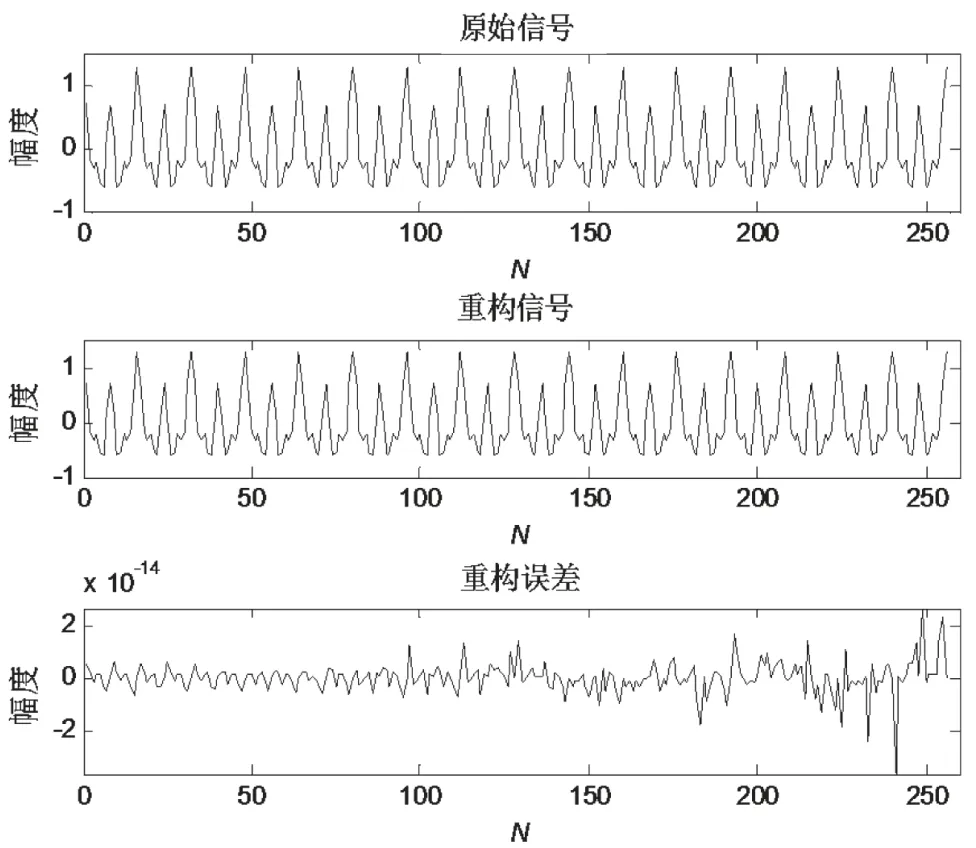
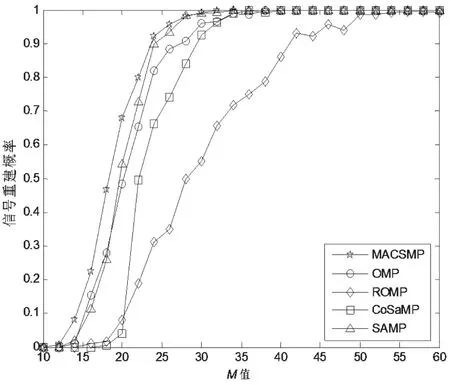
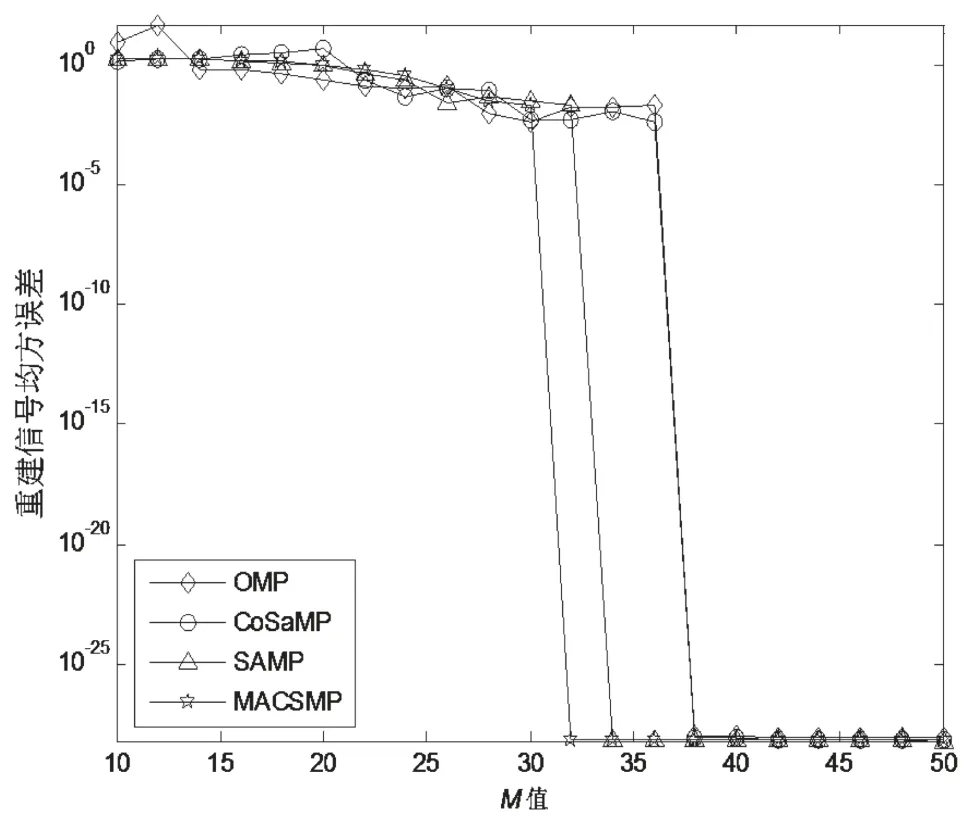
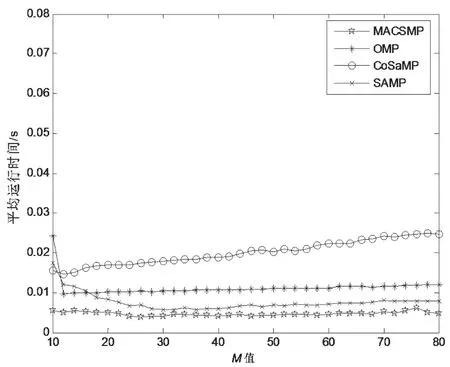
信号在经过上述变换后,我们可以设计出一个M×N(M< 式中Θ=Φ·ψ是一个M×N的矩阵,也被称为恢复矩阵或重构字典。 由于测量向量y的长度相比原信号x的长度要小好多,因此式(2)是一个欠定方程组,通常解不唯一,故无法直接通过求逆运算恢复出信号。此时,可以利用求最小l0范数的办法来解决上述问题,即: 这样就可以将它转换成一个凸优化问题,从而可以使用凸松弛算法来解决这个问题。其中,最为典型的是基追踪(BP)算法[6]。该类算法在信号重建过程中往往需要寻求全局最优解,因而信号重建效果比较好,但相应所需的计算量也比较大,实时性较差。 常用的还有基于l0范数模型的贪婪算法,其由于结构更为简单、速度更快,因而在压缩感知中应用的领域也更加广泛,其中最典型是正交匹配追踪(OMP)算法。此外,还包括引入了正则化的ROMP算法、分段运算的StOMP算法、具有回溯功能的CoSaMP算法以及具有自适应功能的SAMP算法等。 传统CoSaMP重构算法具有回溯的思想,在每次迭代前需计算出残差r,再根据式(5)计算出残差r和测量矩阵里对应原子的相关系数u: 将u中前2K个最大值对应的索引集S合并到支撑集F里,并依据F中的这些索引值取出测量矩阵中相应的原子构成ΦF,再使用最小二乘法重建信号,并只保留F中与信号最为匹配的K个原子的索引,其他元素置零,同时再次更新下ΦF重建信号更新残差rnew: CoSaMP算法在预选阶段选出的原子数是2K个,这一点与其他算法不同。因而,在每次迭代中对信号进行最小二乘估计时,所需的计算量也相对较大。为此,可以引入正则化的思想对原子进行二次筛选,这样既可以减少算法运算量,同时还可以进一步提升算法的精确度。 SAMP算法在使用时无需知晓原始信号的稀疏度,而是利用阶段的累加来不断扩大支撑集大小,使之最终能够达到信号实际稀疏度K,这也是其自适应思想的精华所在。但SAMP算法也受固定步长的限制,因为步长取值过大会影响算法的重构精度,故通常也只是取一个较小的值,这就使得该算法需要多次进行原子匹配以及信号估计,导致算法重建效率较低。 为此,在利用自适应思想解决CoSaMP算法须知晓原始信号稀疏度这一缺陷时,我们还应考虑SAMP算法本身所存在的不足。这里,可以采用稀疏度预估计的办法以及变步长的思想来对其进行改进,以有效提升算法效率和算法精度。下面给出使用的稀疏度预估计方法。 文献[7]证明了,在Φ以参数(K,δK)满足RIP性质前提下。若有K0≥K,则其中K是信号真实稀疏度,K0是稀疏度预估计值,F0为Φ中与残差最匹配的K0个原子对应的索引集。那么,其逆否命题也是真命题。 基于上述理论分析,本文提出了MACSMP算法。该算法首先通过稀疏度预估计的方法获得一个粗略值K0,然后在此基础上使用变步长自适应方式向原始信号真实稀疏度逼近,从而克服了CoSaMP以及SAMP算法中存在的不足。此外,MACSMP算法还增加了正则化方式来进一步筛选原子,保证了其能够更加精准地重构原始信号。下面我们给出MACSMP算法的步骤。 输入:测量向量y,测量矩阵Φ,初始阶段步长step≠0 步骤1:初始稀疏度K0=1,支撑集F=∅; 步骤2:利用式(5)计算相关系数u,并将K0个最大值对应的索引存入支撑集F中; 步骤5:初始化:阶段stage=1,迭代次数n=1,支撑集大小size=K0,索引集S=∅; 步骤6:利用式(5)计算相关系数u,并选出2size个最大值对其进行正则化处理,然后将对应索引存入S中; 步骤7:将S合并到支撑集F中,利用式(6)重建信号xˆ,并保留F中与xˆ最匹配的size个元素,其他元素置零,并更新ΦF; 步骤8:再次重建信号xˆ,同时根据式(7)得到新的残差rnew; 步骤10:若满足扩大支撑集长度条件||rnew||2≥||r||2,则转步骤11;否则r=rnew,迭代次数n=n+1,并转步骤6; 输出:信号x的稀疏估计xˆ 其中,步骤1到步骤3完成稀疏度预估计的功能,步骤6到步骤8主要实现对原子进行正则化筛选以及回溯思想处理,而步骤9到步骤11则是通过两个阈值ε1、ε2来分别控制迭代停止与迭代步长是否减半[8]。MACSMP算法中,逼近信号稀疏度部分的运算量相对较小,主要计算量集中在利用最小二乘法来估计信号这一块,但由于采用稀疏度预估计的方法得到了一个稀疏度粗略值,这样也就间接减少了算法前期迭代中对信号估计的次数,故而能有效降低算法的运算量。 为了检验MACSMP算法性能,文中对其做了相关仿真。在本文实验中,原始信号采用长度为N=256的一维正余弦稀疏信号,阶段步长的值为step=4,稀疏度预估计时参数δK=0.3。此外,稀疏字典ψ和测量矩阵Φ分别采用压缩感知中比较常见的傅里叶变换矩阵和高斯随机矩阵。 图1为M=64时MACSMP算法的重构效果仿真。图中分别给出了原始信号、重构信号以及这两者间的误差,可以发现其能够完整地把信号恢复,并且误差较小。 图1 MACSMP算法的信号重构 为了更进一步说明所提算法的准确性与有效性,下面将其与典型的OMP、ROMP、CoSaMP、SAMP这几种算法作性能对比分析。在M取不同值的情况下,分别用这几种算法对同一信号进行重构,所有算法均运行400次,然后计算其对信号的重建概率及其平均运行时间。 图2是不同M值下MACSMP与上述几种算法对于同一信号的重建结果。可以发现,所有算法对于原始信号的重建概率均随着M值的增大而提高,并且当采样点数M大于一定数量时,所有算法都可以把原始信号完全恢复出来。但在同一采样点数下,本文所提出的MACSMP算法对于信号重构的概率最高,相比而言,其重构性能要优于其他几种算法。 图2 不同M值下的重建概率 图3所示为MACSMP与OMP、CoSaMP以及SAMP算法用于重建同一信号时的均方误差对比。从中可以发现,随着M值的增大,MACSMP算法的均方误差最先趋于零,其次是SAMP算法,然后才是OMP和CoSaMP这两种算法。这直接说明了MACSMP算法仅需更少的采样点就能稳定把信号恢复出来。而图4则是他们各自运行400次的平均运行时间。由图4可知,图中MACSMP算法的运行时间要比其他三种短,说明其重构效率更优。 图3 不同M值下的重建均方误差 图4 各算法仿真所需时间 本文提出了一种改进的稀疏度自适应压缩采样匹配追踪(MACSMP)算法。该算法首先通过稀疏度预估计的方法得到一个初始值,然后在此基础上使用变步长自适应的方式向信号真实稀疏度逼近,克服了CoSaMP以及SAMP算法中存在的不足。除此之外,MACSMP算法还增加了正则化方式来进一步筛选原子,保证了其能够更加精准地重构原始信号。仿真结果显示,在同等条件下,本文所提MACSMP算法要比OMP、CoSaMP、SAMP算法用于重建信号时效果更佳,并且其计算量较低,运行时间较短。 [1] Donoho D.Compressed Sensing[J].IEEE Trans on Information Theory,2006,52(04):1289-1306. [2] Tropp J A,Gilbert A C.Signal Recovery from Random Measurements via Orthogonal Matching Pursuit[J].IEEE Trans on Information Theory,2007,53(12):4655-4666. [3] Needell D,Vershynin R.Uniform Uncertainty Principle and Signal Recovery via Regularized Orthogonal Matching Pursuit[J].Foundations of Computational Mathematics,2009,9(03):317-334. [4] Do T T,Lu Gan,Nguyen N,et al.Sparsity Adaptive Matching Pursuit Algorithm for Practical Compressed Sensing[C].California:Asilomar Conference on Signals,Systems and Computers,2008:581-587. [5] Candes E J,Romberg J K,Tao T.Stable Signal Recovery from Incomplete and Inaccurate Measurements[J].Communications on Pure and Applied Mathemati cs,2006,59(08):1207-1223. [6] Chen S,Donoho D,Saunders M.Atomic Decomposition by Basis Pursuit[J].SIAM Journal on Scientific Computing,1998,20(01):33-61. [7] 杨成,冯巍,冯辉等.一种压缩采样中的稀疏度自适应子空间追踪算法[J].电子学报,2010,8(01):1914-1917. YANG Cheng,FENG Wei,FENG Hui,et al.An Adaptive Subspace Tracking Algorithm for Sparse Degree in Compressed Sampling[J].Journal of Electroni cs,2010,8(01):1914-1917. [8] 朱延万,赵拥军,孙兵.一种改进的稀疏度自适应匹配追踪算法[J].信号处理,2012,28(01):80-86. ZHU Yan-wan,ZHAO Yong-jun,SUN Bing.A Modified Sparsity Adaptive Matching Pursuit Algorithm[J].Signal Processing,2012,28(01):80-86. 倪加明(1992—),男,硕士研究生,主要研究方向为信号处理; 孙钦者(1992—),男,硕士研究生,主要研究方向为软件无线电; 陆家明(1990—),男,硕士研究生,主要研究方向为无线通信技术。 A Modified Adaptive Compressive Sampling Matching Pursuit Algorithm NI Jia-ming, SUN Qin-zhe, LU Jia-ming For the reconstruction of signals with unknown sparsity , a modified sparsity adaptive compressive sampling matching pursuit (MACSMP) algorithm is proposed. Based on the compressive sampling matching pursuit (CoSaMP) algorithm, the proposed algorithm adds the thought of regularizaton to iterative process,thus to improve the accuracy of the algorithm, and in combination with variable step adaptive idea, to solve the dependence on signal sparsity. Simulation results indicate that the proposed MACSMP algorithm is better than SAMP algorithm, OMP algorithm, CoSaMP algorithm in the reconstruction performance and operation efficiency, and in addition the calculation is lower and the running time shorter. compressed sensing; reconstruction algorithm; sparsity adaptation; regularization TN911.7 A 1002-0802(2016)-08-0992-05 10.3969/j.issn.1002-0802.2016.08.007 2016-04-18; 2016-07-25 date:2016-04-18;Revised date:2016-07-25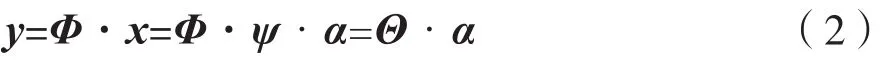
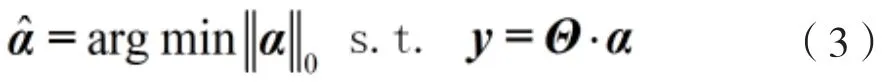
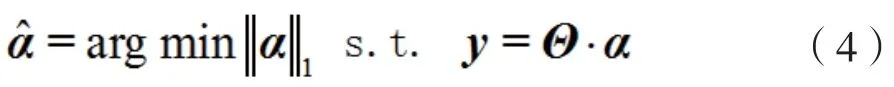
2 MACSMP算法
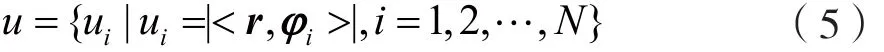

3 仿真结果
4 结 语

(College of Communication Engineering, Hangzhou Dianzi University, Hangzhou Zhejiang 310018, China)
