新的最佳非对称量子码和最佳量子卷积码*

陈丙亚

（安徽理工大学 理学院，安徽 淮南 232007）

新的最佳非对称量子码和最佳量子卷积码*

陈丙亚

（安徽理工大学 理学院，安徽 淮南 232007）

量子MDS码是一类重要的量子码。目前，许多学者利用常循环码构造量子MDS码。通过研究常循环码，得到两类新的非对称量子码，且对于相位翻转错误和量子比特翻转错误具有更大的纠错能力。由常循环码得到的两类新的量子卷积码，和之前文献中的不同。经验证，所构造的非对称量子码和量子卷积码是最佳的。

常循环码；非对称量子码；量子卷积码；最佳码

0　引 言

量子纠错码的构造一直是量子信息和量子计算方面重要的研究课题。当前，一些学者在研究常循环码构造量子码[1-8]。众所周知，常循环码包括循环码和负循环码。2013年，Kai[9]等人利用负循环码构造两类量子MDS码。同年，Kai、Zhu[10]又用负循环码构造几类好的量子码。2014年，Kai[11]等人又用几类常循环码构造几类量子MDS码。Chen[12]等人则研究与文献[11]中不同的几类常循环码，并构造出量子MDS码。Zhang、Chen[13]用常循环码构造两类新的量子码。现在，常循环码已经成为量子研究方面好的资源。

非对称量子码是定义在有不同性质的量子比特翻转错误和相位翻转错误的量子通道上的量子码。在许多量子力学系统中，量子比特翻转和相位翻转是不同的。过去的二十年，好的非对称量子码[14-19]一直被研究。Chen[20]等人利用负循环码研究最佳非对称量子码。Wang、Zhu[21]则用常循环码构造六类新的非对称量子码。

现在，好的量子卷积码[22-26]的构造一直被许多学者研究。Guardia[27]利用几类循环码构造一些好的量子卷积码，并和文献[22]中的量子卷积码做了比较。Guardia[28]又用BCH循环码研究了一类最佳量子卷积码，同时也利用负循环码构造两类最佳量子卷积码[29]，还用常循环码构造了几类最佳卷积码和非对称量子码[30]。

本文将利用文献[13]中的两种常循环码构造两类非对称量子码和量子卷积码，具体如下：

（4）[[8(q-1),8(q-1)-2δ'+2,1;1,δ'+1]]q，其中q是奇素数幂且q=8t-1，t是偶正整数，δ'是正整数，且

本文结构如下：第一部分介绍常循环码的一些定义和基本结论。第二部分，复习非对称量子码的一些定义和基本结论，构造两类最佳非对称量子码。第三部分，首先介绍经典卷积码和量子卷积码的概念和结论，然后构造两类最佳量子卷积码。最后总结全文。

1　常循环码的基本知识点

首先，介绍常循环码的基本结论[11-12]。

若C⊆C⊥h，则C是Hermitian自正交码。若C⊥h⊆C，则C是Hermitian对偶包含码。

性质1[13]（常循环码的BCH边界）：假设gcd(n,q)=1，令C是长度为n的q2元λ常循环码。若C的生成多项式g(x)有元素作为根。其中，η是单位本原rn次根，则C的最小距离至少是d。

2　最佳非对称量子码的构造

首先陈述一些定义和基本结论[14-18]，然后用文献[13]中的两类常循环码构造两类最佳非对称量子码。

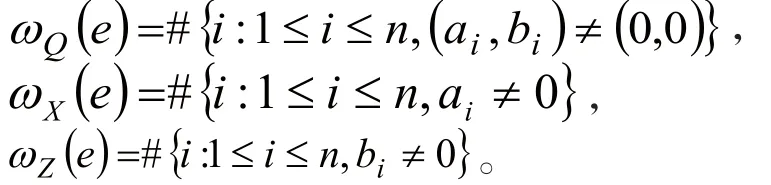
定义1[14]：参数为gcd(n,q)=1的q元非对称量子码Q是Hilbert空间Γqn的一个qk维子空间，且Q能够纠正至多个量子比特翻转错误和个相位翻转错误。

定理1对Euclidean和Hermitian两种情况都成立，具体如下。

定理1[15]（CSS构造）：令Ci是参数为[n,ki,di]的经典码，i=1,2，有则存在参数为的非对称量子码。其中，

性质2[8]（Singleton界）：若线性码C=[n,k,d]存在，则k≤n-d +1。

性质3[20]：C是参数为[[n,k,dz/dx]]的非对称量子码，则C满足量子Singleton边界k≤n-dzdx+2。若C满足等式k =n -dz-dx+2，则C是最佳码。

引理1[13]：假设q是一个奇素数幂，且q≡3(mod4)。令n =(q2-1)4，r=4。设C是Fq2上长度为n，定义集合为：

定理2：假设q是一个奇素数幂，且q≡3(mod4)。令n =(q2-1)4，r=4，则存在参数为[[(q2-1)4,(q2-1)4-(δ1+δ2),δ1+1/δ2+1]]的非对称量子码。其中，δ1、δ2是正整数，且

证明：n =(q2-1)4，r=4。令是单位本原四次根。模rn的每个q2元分圆陪集恰好包含一个元素。假设Cδ是Fq2上长度为n的λ循环码，其定义集合为：

式中δ是正整数，且

令C1是定义集合为：的λ常循环码。

于是，根据性质1和引理1可知，C1是参数为[(q2-1)4,(q2-1)4-δ,d≥δ+1]2的λ常循111q环码。根据性质2知，C1是λ常循环码

令C2是定义集合为的λ常循环码。

于是，根据性质1和引理1可知，C2是参数为[(q2-1)4,(q2-1)4-δ2,d2≥δ2+1]q2的λ常循环码。根据性质2知，C2是λ常循环码

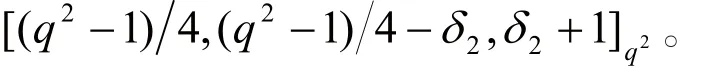
其中，δ1、δ2是正整数，且

注1：由性质3知，所构造的非对称量子码是最佳的。

引理2[13]：假设q是奇素数幂，且q=8t-1，t是偶正整数。令n=8(q-1)，r=t。假设C是上长度为n、定义集合为Z={1+ti|4t-8≤i≤8t-3}的λ常循环码，则C是对偶包含码。

定理3：假设q是奇素数幂，且q=8t-1，t是偶正整数。令n=8(q-1)，r=t，则存在参数为[[8(q-1),8(q-1)-(δ1+δ2),δ1+1δ2+1]]q2的非对称循环码。

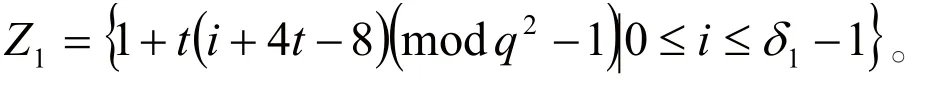
其中，δ1是正整数，且

根据性质1和引理1知，C1是参数为[8(q-1),8(q-1)-δ1,d1≥δ1+1]q2的λ常循环码。

令C2是定义集合为：的λ常循环码，

[8(q-1),8(q-1)-δ2,d2≥δ2+1]q2的λ常循环码。

因此，由定理1知，存在参数为

[[8(q-1),8(q-1)-(δ1+δ2),δ1+1δ2+1]]q2的非对称量子码。

注2：由性质3知，构造的非对称量子码是最佳的。

例1：根据定理2、定理3，得到一些非对称量子码，分别如表1、表2所示。在表3中，我们列举了文献[21]定理4.3中的一些非对称量子码。

表1　由定理2得到的一些非对称量子码

表2　由定理3得到的一些非对称量子码

表3　由文献[21]中的定理4.3得到的一些非对称量子码

固定码长和维数，比较关于相位翻转错误和量子比特翻转错误的最小距离dz/dx。通过研究表1、表2、表3，发现在相同码率下，表1和表2中dz和dx的取值更大，即dz/dx可取到较大的值。所以，定理2和定理3构造的非对称量子码对相位翻转错误和量子比特翻转错误具有更大的纠错能力。

文献[15]中，G.G.La Guardia用RS码构造非对称量子码p是素数。用表1和表2构造的两类最佳非对称量子码和文献[15]中的进行比较，发现定理2和定理3构造的两类非对称量子码的较大边界dz比较小边界dx大。所以，文中构造的非对称量子码对相位翻转错误和量子比特翻转错误具有更大的纠错能力。

3　最佳量子卷积码的构造

首先介绍经典卷积码和量子卷积码的一些定义和基本结论[22-23,26-28]，然后利用常循环码构造两类量子卷积码。

若G(D)是正逆多项式，则称多项式编码矩阵G(D)∈Fq[D]k×n是基本的。假如整体约束长度在卷积码C的所有基本生成矩阵中有最小值，则卷积码C的基本生成矩阵是截短的。所以，整体约束长度γ是卷积码C的阶次。定义元素的权重为其中，wt（ vi（ D））是vi（D）的非零系数的数量。

定义2[22-23]：码率为kn的卷积码是由截短基本矩阵生成的的一个子模块，

卷积码C的Euclidan对偶为：

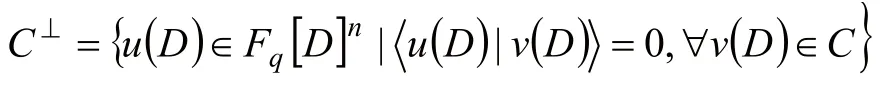
下面介绍经典卷积码的基本结论[22-23,26,28-30]。

令[n,k,d ]q是奇偶校验矩阵H的块码，矩阵H被分割成μ+1个不相交的子矩阵Hi，使得H=［H0,H1,…,Hì］T。其中，每个Hi有n列。因此，多项式矩阵：

矩阵G（D）生成卷积码V。其中，G（D）有κ行，κ是矩阵Hi中行的最大数量。矩阵是通过在矩阵Hi底端增加元素为零的行得到的，使得矩阵一共有κ行。

下面的结论对Euclidean和Hermitian两种情况都成立。

定理4[28-30]：令是奇偶校验矩阵为的[n,k,d ]q码。假设H被分割成子模块使得对1≤i≤μ，κ=rkH0， rkHi≤κ。考虑式（1）中的矩阵G（D），则有：

（a）矩阵G（D）是截短基本生成矩阵。

（b）若C⊥⊆C（相对应C⊥h⊆C），则卷积码V=｛v（D）=u （D）G（D）|u（G）∈Fqn-k[D]｝满足V⊂V⊥（相对应V⊂V⊥h）。

（c）若df和分别表示V和V⊥的自由距离，di表示码的最小距离，d⊥是码C⊥的最小距离，则码有

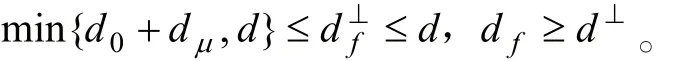
下面介绍量子卷积码的基本结论[22-23,28-29]。

稳定子可由形式为S（ D）=（X（ D）|Z（ D））∈F[D](n-k)×2nq的矩阵给出，满足X（D）Z（1D ）t-Z（D）X （1D）t=0。考虑由满秩稳定子矩阵S（D）定义的量子卷积码C。则C是码率为kn的量子卷积码[(n, k,μ; γ,df)]q。其中，n是帧大小，k是每个帧上逻辑量子数的数量。量子卷积码的存储量df是自由距离，γ是码的阶次。定义约束长度为则整体约束长度是

下面定理给出如何用经典卷积码构造量子卷积稳定码。

定理5[22-23]令C是参数为的卷积码，有C⊆C⊥h。于是，存在量子卷积稳定码[(n, k,μ; γ,df)]q。其中df=wt( C⊥hC)。

性质4[22,23]（量子Singleton界）：Fq2上纯的线性卷积稳定码[(n, k,μ; γ,df)]q的自由距离为

定理6：假设q是奇素数幂，且q≡3(mod4)。令n =(q2-1)4，r=4，则存在参数为[(q2-1)4,(q2-1)4-2δ′+2,1;1,δ′+1)]q的量子卷积码。其中，

证明：令C是定义集合为

所以，存在参数为[(q2-1)4,(q2-1)4-δ′, δ′+1]q2的λ常循环码。

同样，令C0是定义集合为

Z0=C4-q∪C8-q∪…∪C4δ′-4-q 的λ常循环码。从引理4知，C0的奇偶校验矩阵为：

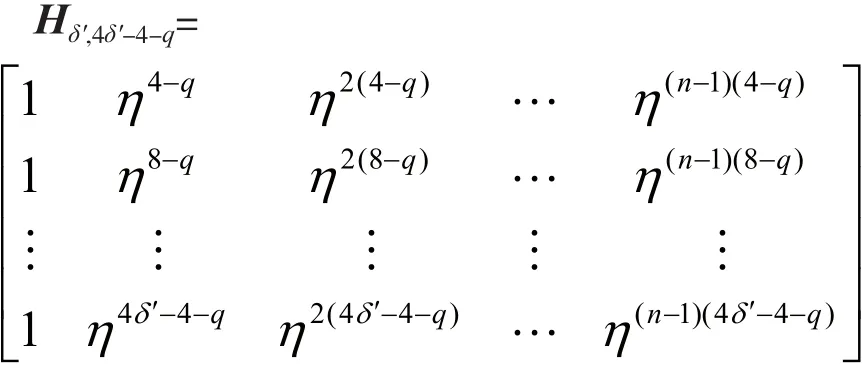
所以，存在参数为

[(q2-1)4,(q2-1)4-δ′+1,δ′]q2的λ常循环码。

假设C1是Fq2上定义集合为Z1=C4δ′-q的λ常循环码。根据引理4知，C1的奇偶矩阵H1为

所以得到参数[(q2-1)4,(q2-1)4-1,d≥2]q2的λ常循环码。

根据上面的讨论，得到rkH0≥rkH1。因此，由矩阵生成的卷积码V是参数为的λ常循环码。其中，是通过在H1底端增加元素为零的行而得到，使得和H0的行数相等。因为那么根据定理4得到由定理4和引理1知

因此，由定理2知，存在量子卷积码

定理7：假设q是奇素数幂，且q=8t-1，t是偶正整数。令n=8(q-1)，r=t，则存在量子卷积码[[8(q-1),8(q-1)-2δ′+2,1;1,δ′+1]]q。其中，

令λ常循环码C0、C1的定义集合分别为其中

因此，使用和定理6相同的方法可证明结论成立。

例2：根据定理5、定理6，得到一些量子卷积码，分别如表4、表5所示。

表4　由定理5得到的一些量子卷积码

表5　由定理6得到的一些量子卷积码

和文献[25,28-31]构造的量子卷积码比较，发现本文构造的卷积码和它们均不相同。

4　结 语

常循环码用于构造最佳量子码是一类好的资源。通过研究文献[13]中的常循环码，构造两类最佳非对称量子码和两类最佳量子卷积码。通过比较分析得出，文中构造的非对称量子码比文献[21]中的定理4.3和文献[15]中的非对称量子码对相位翻转错误和量子比特翻转错误具有更大的纠错能力。表4、表5分别列举了一些最佳量子卷积码，证明文中构造的量子卷积码和文献[25,28-31]不同。

[1] Aydin N,Siap I,Ray-Chaudhuri D K.The Structure of 1-generator Quasi-twisted Codes and New Linear Codes[J].Designs Codes & Cryptograp hy,2001,24(03):313-326.

[2] Bakshi G K,Raka M.A Class of Constacyclic Codes over a Finite Field[J].Finite Fields & Their Applicati on,2012,18(02):362-377.

[3] Berlekamp E R.Negacyclic Codes for the Lee Metric[J].Combinatorial Mathematics & Its Applications,2015:298-316.

[4] Blackford T.Negacyclic Duadic Codes[J].Finite Fields & and Their Applications,2008,14(04):930-943.

[5] Chen B,Fan Y,Lin L,Liu H,et al.Constacyclic Codes over Finite Fields[J].Finite Fields & and Their Applicatio ns,2013,18(06):1217-1231.

[6] Huffman W C,Pless V.Foundamentals of Error-Correcting Codes[M].Cambridge:Cambridge University Press,2003.

[7] Krishna A,Sarwate D V.Psudocyclic Maximum-distanceseparable Codes[J].IEEE Transactions on Information Theory,1990,36(04):880-884.

[8] MacWilliams F J,Sloane N J A.The Theory of Error-Correcting Codes,Part I[M].Cambridge:Cambridge University Press,1977,26(13):Xviii,646.

[9] Kai X,Zhu Z.New Quantum MDS Codes from Negacyclic Codes[J].IEEE Transactions on Information Theory,2013,59(02):1193-1197.

[10] Kai X,Zhu S,Tang Y.Quantum Negacyclic Codes[J]. Physical Reviewa.A,2013,88(01):012326.

[11] Kai X,Zhu Z,Li P.Constacyclic Codes and some New Quantum MDS Codes[J].IEEE Transactions on Information Theory,2014,60(04):2080-2086.

[12] Chen B,Ling S,Zhang G.Application of Constacyclic Codes to Quantum MDS Codes[J].IEEE Transactions on Information Theory,2014,61(03):1474-1484.

[13] Zhang G,Chen B.New Quantum MDS Codes[J].International Journal of Quantum Information,2014,12(04):1450019.

[14] La Guardia G G.New Families of Asymmertric Quantum BCH Codes[J].Quantum Information & Computation,2011,11(03-04):239-252.

[15] La Guardia G G.Asymmetric Quantum Reed-Solomon and Generalizde Reed-Solomon Codes[J].Quantum Information Processing,2012,11(02):591-604.

[16] La Guardia G G.Asymmertric Quantum Product Codes[J]. Internation Journal of Quantum Information,2012,10(01).

[17] La Guardia G G.Asymmetric Quantum Codes:New Codes from Old[J].Quantum Information Processi ng,2013,12(08):2771-2790.

[18] La Guardia G G.On the Construction of Asymmertric Quantum Codes[J].Interational of Theortical Physics,2014,53(07):2312-2322.

[19] Leng R G,Ma Z.Constructions of New Families of Nonbinary Asymmertric Quantum BCH Codes and Subsystem BCH Codes[J].Science China Physics Mechanics & Astronomy,2012,55(03):465-469.

[20] Chen J Z,Li J P,Lin J.New Optimal Asymmetric Quantum Codes Devived from Negacyclic Codes[J].InTernational Journal of Theoretical Physics,2013,53(01):72-79.

[21] Wang L,Zhu S.On the Construction of Optimal Asymmertric Quantum Codes[J].International Journal of Quantum Information,2014,12(03):856-863.

[22] Grassl M,Rotteler M.Non-catastrophic Encodrs and Encoders Inverses for Quantum Convolutional Codes[J].Proc.IEEE Intl.Symposium on Information Theory(ISIT),2006:1109-1113.

[23] Grassal M,Rotteler M.Constructions of Quantum Convolutional Codes[J].IEEE International Symposium on Information Theory,2007,28(31):816-820.

[24] Aly S A,Grassl M,Klappenecker A,et al.Quantum Convolution BCH Codes[J].Mathematics,2007:180-183.

[25] Aly S A,Klappenecker A,Sarvepalli P K.Quantum Convolutional Codes Derivede from Reed-Solomon and Reed-Muller Codes[C].IEEE International Symposium on Information Theory.Nice:IEEE,2007:821-825.

[26] Forney Jr G D,Grassl M,Guha S.Convolutional and Tail-biting Quantum Error-Correcting Codes[J].IEEE Transactions on Information Theory,2007,53(03):865-880.

[27] G.G.La Guardia.On Nonbinary Quantum Convolutional BCH Codes[J].Quantum Information & Computati on,2012,12(09-10):820-842.

[28] La Guardia G G.On Classical and Quantum MDSConvolutional BCH Codes[J].IEEE Transactions on Information Theory,2012,60(01):304-312.

[29] La Guardia G G.On Negacyclic MDS-Convolutional Codes[J].Linear Algebra & Its Applicatio ns,2014,448(03):85-96.

[30] La Guardia G G.On Optimal Constacyclic Codes[J]. Eprint Arxiv,2013(496):594-610.

[31] Chen J Z,Li J P.Some Families of Asymmertric Quantum Codes and Quantum Convolutional Codes from Constscyclic Codes[J].Linear Algebra and Its Applications,2015(475):186-199.

陈丙亚（1990—），女，硕士，主要研究方向为纠错码理论及应用。

Novel Optimal Asymmetric Quantum Code and Optimal Quantum Convolutional Code

CHEN Bing-ya
(College of Science, Anhui University of Science and Technology, Huainan Anhui 232007, China)

Quantum MDS (maximal-distance-separable) code is an important class of quantum codes. Recently, many scholars utilize constacyclic codes to construct some quantum MDS codes. Based on the research of constacyclic codes, two new classes of asymmetric quantum codes are achieved,and they have even greater error-correction capability than the original in regard to phase flip error and quantum bit flip error. Quantum convolutional codes from constacyclic codes are different from the ones mentioned in the lierature. Demonstration indicates that, the constructed asymmetric quantum codes and quantum convolutional codes are optimal in performance.

constacyclic cod;asymmetric code;quantum convolutional code;optimal code

National Science Foundation of Anhui Province(No.1408085MA05)

TN911.2

A

1002-0802(2016)-08-0968-07

10.3969/j.issn.1002-0802.2016.08.003

2016-04-21;

2016-07-22

date:2016-04-21;Revised date:2016-07-22

安徽省自然科学基金（No.1408085MA05）