FTN系统中的低复杂度接收技术比较*

张广娜，郭明喜，沈越泓

（解放军理工大学 通信工程学院，江苏 南京 210007）

FTN系统中的低复杂度接收技术比较*

张广娜，郭明喜，沈越泓

（解放军理工大学 通信工程学院，江苏 南京 210007）

超奈奎斯特码元速率传输（Faster-than-Nyquist）可以有效提高系统的带宽有效性和通信系统的传输速率，但在接收端不可避免地引入无限长的码间串扰（ISI），增加了接收设备特别是接收机的复杂度。为了降低接收端的复杂度，重点介绍FTN传输系统中的低复杂度接收技术及其改进方案，包括加窗Chase均衡（WCE）和改进型WCE、迭代分组判决反馈均衡器（IBDFE）和低复杂度IBDFE（LC-IBDFE）、判决反馈均衡（DFE）和部分判决反馈均衡（PDFE），同时分别从计算复杂度和系统误码率性能两个方面进行分析比较，给出各方法的优缺点及应用场合。

超奈奎斯特码元速率传输；码间串扰；低复杂度；接收技术

0　引 言

1975年，Mazo首次提出了FTN理论[1]，通过理论证明，在带宽受限的加性高斯白噪声信道条件下，当以超过Nyquist速率25%以内的速率传输sinc脉冲时，二进制调制符号之间的欧氏距离并没有损失，误码率性能可以不下降。所以，和传统方法相比，该方法可以在相同带宽、相同能量且不损失性能的情况下，传输更多的数据符号[2]。

由于FTN比传统的Nyquist准则提供了更高的符号速率，系统接收端必然引入无限长的码间串扰。如何在消除码间串扰的同时以较低的复杂度完成FTN系统的检测，成为制约FTN技术迅速发展的重要因素。当传输的码字等概率分布时，最大似然检测（MLSD）是最佳的[3]。对于长ISI信道，MLSD的计算复杂度随滤波器的抽头数和符号的比特数的增加呈指数级别增加，难以应用于实际的通信系统。维特比算法（VA）同样存在FTN系统不可接受的高复杂度[4]。除此之外，人们提出了将低复杂度的BCJR算法应用于FTN系统的ISI消除[5-6]，但是计算网格解码的复杂度比较困难。McGuire和Sima也提出了一种在加性高斯白噪声信道条件下采用矩阵乘法降低接收复杂度的离散块FTN信号的方法。

本文从降低FTN系统接收复杂度的角度出发，重点介绍FTN传输系统中的低复杂度接收技术及其改进方案，包括WCE和FTN-MWCE、IBDFE和LC-IBDFE、DFE和PDFE。对每种低复杂度接收技术及其改进技术分别进行分析比较，并指出其优缺点和适用范围，以期为FTN传输技术的实用化奠定基础。

文章结构如下：第一部分给出了FTN系统传输模型。第二部分介绍并比较上述三种低复杂度接收技术及其改进方案，并分别给出其复杂度和BER性能差异。第三部分对本文提出的低复杂度接收方案作进行总结并得出结论。第四部分归纳全文，展望下一步工作。

1　系统模型

FTN系统如图1所示。由图1可看出，信道编码和调制解调与传统Nyquist速率传输并无太大区别，最大的区别在于FTN脉冲成型和FTN的检测模块。本文从FTN的检测模块入手，重点介绍三种FTN传输系统中的低复杂度接收技术及其改进方案：（1）基于Chase算法的均衡；（2）频域均衡；（3）基于矩阵模型的接收技术。三种接收技术及其改进技术均可以有效降低接收复杂度，但其优缺点及适用范围各不相同。第二部分我们将对每种方法做详细介绍及比较，从而进一步将FTN传输技术推向实用化。

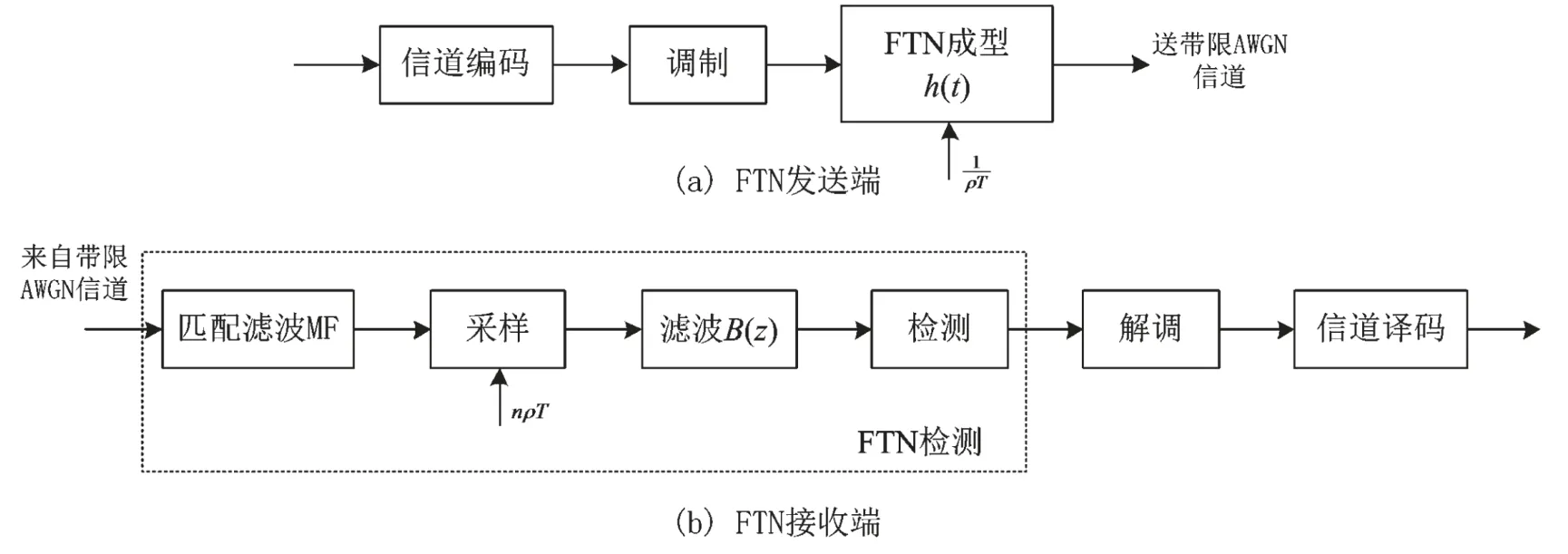
图1　FTN系统传输模型

2　低复杂度接收技术

2.1基于Chase算法的均衡

1972年，Chase提出了用于线性分组码的3种译码算法，即Chase算法[7]。Tang[8]证明，Chase译码算法的纠错半径如果达到最大值，则一定是渐进最优的。但由于Chase算法主要用于分组码和Turbo乘积码的软判决、多进多出信道检测以及多用户检测，译码过程中将会产生大量的试探序列，复杂度还有待进一步降低。

2.1.1加窗Chase均衡

文献[9]提出了加窗Chase均衡。该方法可以使系统具有逼近MLSD的误码性能，同时对接收序列做加窗处理。当窗口内出现可信度低的值需重新传输时，只需重新传输窗口内的序列，从而避免Chase算法的复杂度随数据长度呈指数增长。为消除接收矢量中的ISI影响，加窗Chase均衡采用两级均衡，接收方案框图如图2所示，具体计算步骤如下。

时间离散的基带系统的第k个接收样值信号表示为：

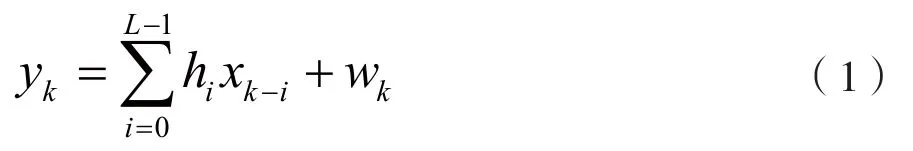
式中，L为ISI长度，hi为第i个信道系数，wk为零均值、方差为σ2的复数加性高斯白噪声（AWGN）。一组信息比特经星座符号映射得到M进制符号xi=F(di)，m=log2M。式（1）的矩阵形式为：

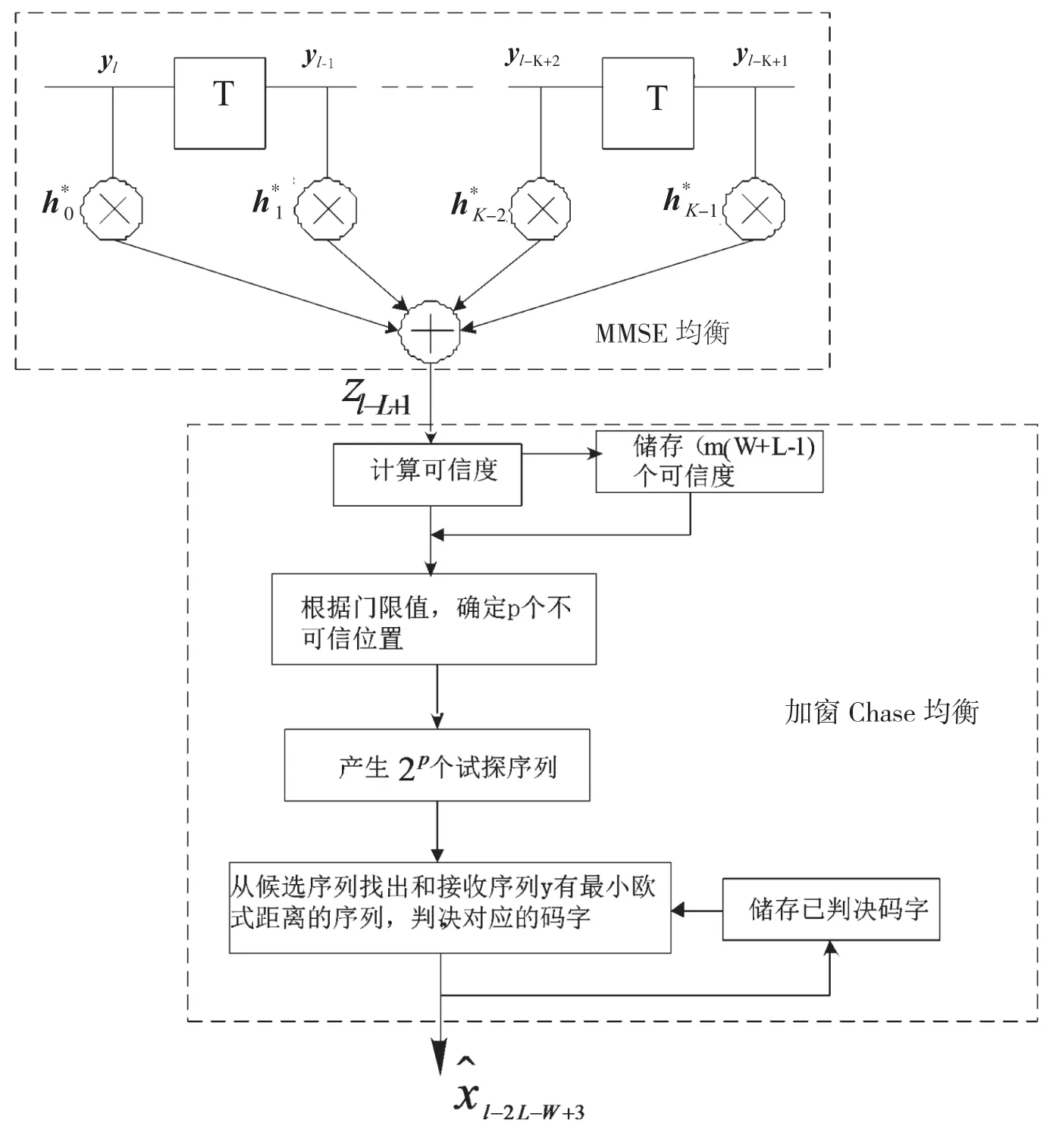
图2　FTN-WCE接收方案系统

式中，yk、wk、h均为长度为N0的矢量，发送矢量Xk为N0×L矩阵，其第i行可表示为

（1）MMSE均衡

（2）加窗Chase均衡

步骤2：选取最不可信位置。

步骤3：产生试探序列。

步骤4：输出译码。

文献[9]给出了每个步骤的详细过程，这里不再赘述。

2.1.2改进型WCE

为进一步降低加窗Chase均衡的复杂度，文献[10]提出了改进型WCE，主要从以下两点对加窗Chase均衡进行改进：第一，将Chase算法产生的发送信号候选试探序列变传统的二进制编码排列为格雷编码排列，由于相邻的两个候选试探序列只存在一个不同比特，通过数学推导，可以得到迭代的欧氏距离计算方法，从而减少运算量；第二，设计一种更简单、更高效的序列判决准则，而文献[9]中一次窗口内Chase算法的执行只能对应一个判决符号的输出。将上述改进型WCE和新的低复杂度判决准则相结合，可实现保持误码性能不变的同时，有效降低计算复杂度。

2.1.3比较与分析

（1）复杂度分析

相较于加窗Chase算法，改进型WCE带来的复杂度降低体现在计算试探序列与接收序列的欧氏距离上。表1给出了两种检测算法平均每窗口内的计算复杂度。可见，改进型WCE在复乘和复加计算量上都有大幅度降低。

表1　两种检测算法平均每窗口内的计算复杂度比较

其中，W和W '分别为加窗Chase均衡和改进型WCE中设置的窗口长度，分别为两种方法中平均每窗口内的试探序列个数。因此，总的复乘和复加计算的减少率分别为：

（2）误码率性能分析

在AWGN信道条件下采用BPSK调制，即m=1，ISI长度L=11，MMSE均衡器长度K=31，信道系数h=[0.04 -0.05 0.07 -0.21 -0.5 0.72 0.36 0 0.21 0.03 0.07]T。

图3是窗口长度W '=11、门限Vth=0.5时，MMSE均衡法、加窗Chase均衡和改进型WCE的误码率性能随信噪比的变化曲线。可以看到，MMSE均衡法的误码性能最差。采用改进型WCE对FTN传输系统进行接收，和加窗Chase算法相比，误码率性能没有下降，且都接近MLSD的误码性能。

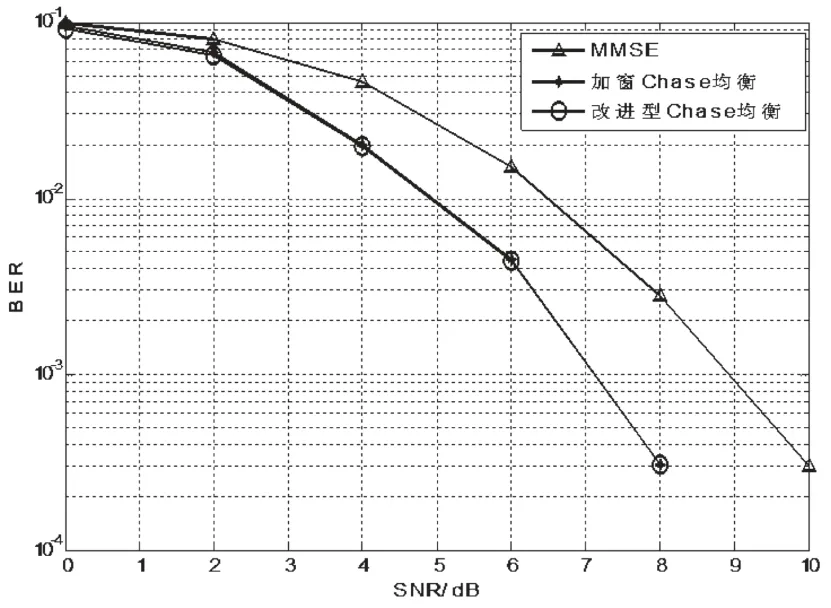
图3　三种均衡方式误码率性能比较

2.2频域均衡

2.2.1IBDFE的简要介绍

对于普通的二进制线性调制信号，其基带形式为：

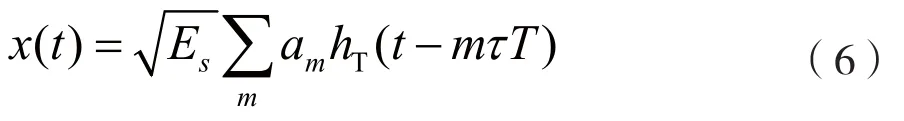
式中am是等概独立同分布的实数数据符号；对FTN信号，hT(t)是实的非正交单位能量基带调制脉冲，且符号时间为τT(0＜τ＜1)。为方便接收端的有限长均衡器操作，需要对无限长ISI做近似截短处理，截短后的ISI长度是L[11]。经过加性高斯白噪声（AWGN）信道和接收滤波器，并以两倍的发送速率过采样后，得到接收信号：

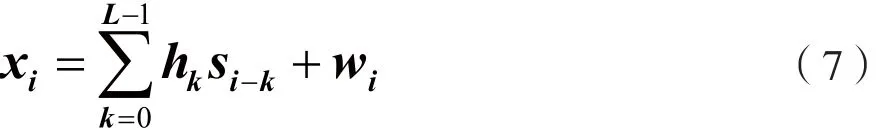
式中，hk=h(kT/2),k=0……Nh-1。wi是加性高斯白噪声与接收滤波器冲激响应的卷积，其中加性高斯白噪声的单边功率谱密度是n0。IBDFE结构简图如图4所示。

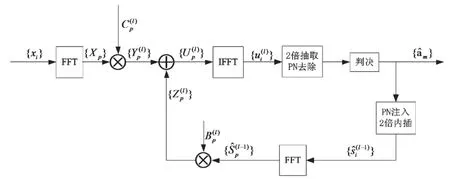
图4　IBDFE结构

IBDFE的主要步骤为：

步骤1：伪随机噪声（PN）扩展

发送信号分组前，发送端首先要发送一个长为n的PN序列{qm}。{qm}在接收端已知，再在长度为（P-n）的数据分组{dm}后增加长度为n的PN序列{qm}组成信号分组，发送信号的结构如图5所示。这里系统不采用循环前缀（CP）扩展传输方式，原因是PN传输扩展方式性能更优[12]。为了避免相邻两个分组内的数据符号相互影响，PN序列长度n必须大于等于ISI的长度，即：n≥(L-1)/2。

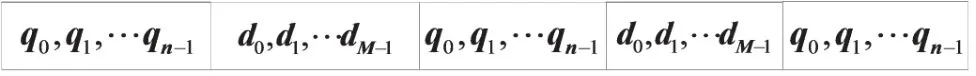
图5　发送信号的结构

步骤2：DFT变换

由图4可知，IBDFE由前向滤波器和反向滤波器两部分组成。接收到的信号{xi}经过DFT变换得到：

由于采用过采样，因此在接收端信号分组长度、分组中信息序列长度、PN序列长度均为原长度的两倍，即p=0,…2P-1，Xp、Sp、Hp分别是xi、si、hp的2P点DFT变换，Wp是wi的2P点DFT变换。

步骤3：迭代运算

设迭代次数为υ，最大迭代次数为NI(υ=1,2,…NI)，则第υ次迭代后的信号Up(υ)表示成：

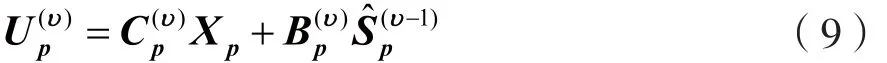
步骤4：计算前向、反向抽头系数

文献[13]给出了该均衡器的前向和反向抽头系数的具体表达形式，并在文献[14]中给出了主要参数的详细估计方法。由于均衡器每进行一次迭代，参数都要计算一次，因此IBDFE的复杂度很高。

2.2.2LC-IBDFE

在接收机结构上，文献[15]所提的LC-IBDFE与IBDFE结构相同，创新点在于其为了降低复杂度，先将判决信号中的误差与期望信号分离，即频域判决信号表示为：

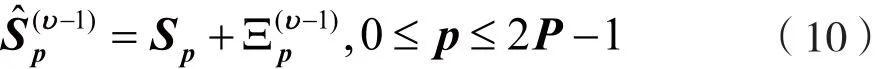
2.2.3比较与分析

（1）复杂度分析

IBDFE、LC-IBDFE两种均衡器的计算复杂度主要来自三方面：（1）DFT、IDFT计算；（2）DFE接收机处理信号；（3）抽头系数的计算和参数估计。其中，（1）（2）产生的运算量相同，不同点体现在抽头系数的计算和参数估计。文献[15]给出了两种均衡器判决单个符号所需运算量，如表2所示。

表2　两种均衡器判决单个符号所需运算量

比较得到，计算LC-IBDFE的前向、反向抽头系数时，每个信号分组不随迭代次数的增加而更新，只需计算一次。因此，在高迭代次数的条件下，LC-IBDFE的复杂度优势将更明显。文献[15]同样通过仿真验证了这一点。

（2）误码率性能分析

在AWGN信道条件下采用BPSK调制，ISI长度为L=81，升余弦滚降系数α=0.2，加速因子τ分别取0.9、0.8，PN长度为n=40，分组长度P=256。LC-IBDFE中β=2，设定Ps,pre=0.1，图6给出了当迭代次数NI=2时的两均衡器性能比较。可以看出τ值相同时，两种接收机在性能上很接近，并且都随τ值的减小性能变差。

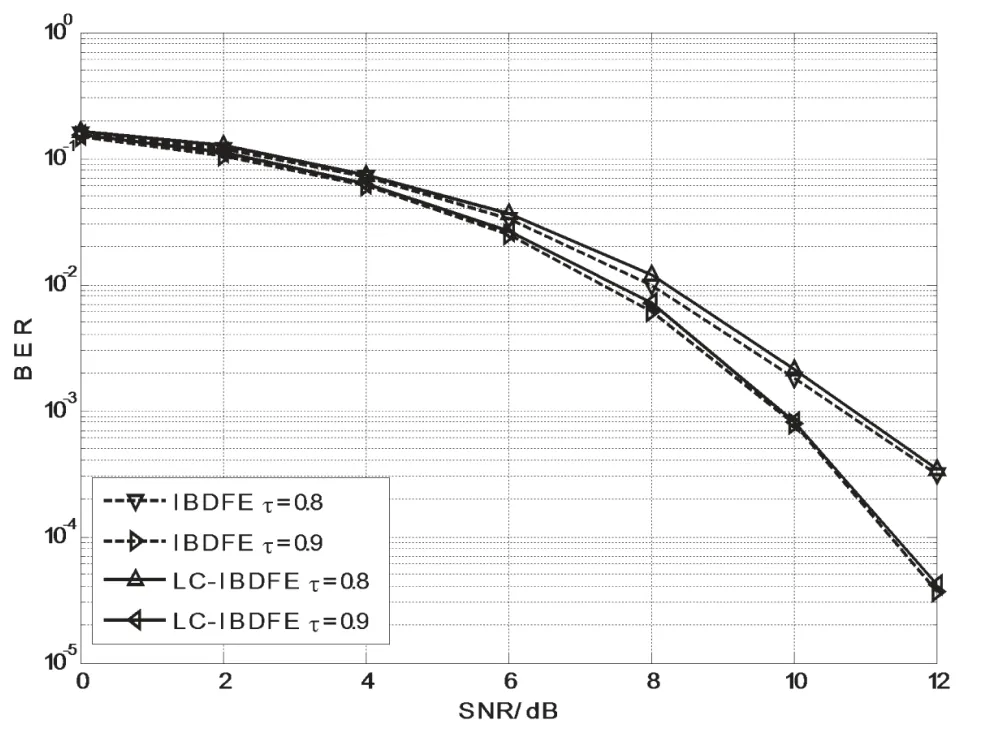
图6　NI=2时，LC-IBDFE和IBDFE的性能

2.3基于矩阵模型的接收技术

图7给出了FTN的系统模型。

图7　FTN系统模型

FTN信号经过AWGN信道得到接收信号，再经过匹配滤波和采样后得到矩阵表达式为：

式中，w是有色高斯噪声序列，噪声的协方差矩阵为σ2H，矩阵H表示FTN信号引入的符号间干扰，取截短后的ISI维度为N×N。对于根升余弦调制脉冲h(t)，ISI矩阵可以表示为[16]：

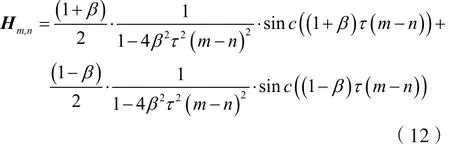
2.3.1判决反馈均衡（DFE）

采用迫零算法是信号检测最简单直接的方法，即接收信号向量Y左乘干扰矩阵的Moore-Penrose逆矩阵。但是，该方法会使噪声幅度增加而使误码率性能变差。文献[17]将MIMO系统常用的基于矩阵QR分解的DFE信号检测应用于FTN信号系统中。该算法的主要步骤为：

（1）QR分解

对ISI矩阵H做QR分解得到：

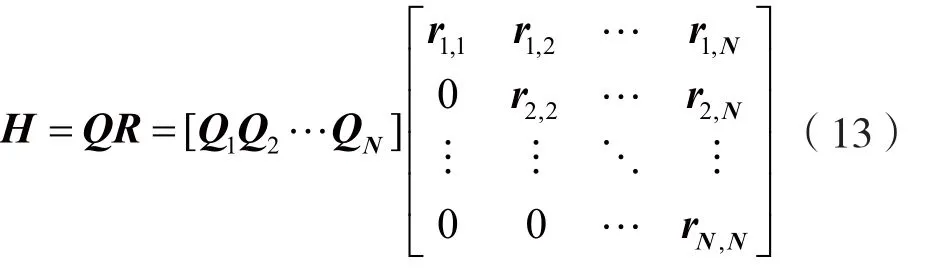
式中R是上三角矩阵，Q满足QHQ=I，为酉矩阵。

（2）左乘QH

将接收信号向量Y左乘QH得到：

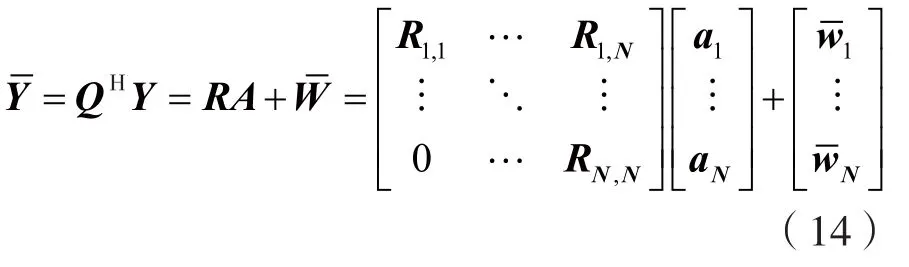
（3）硬判决

从式（14）的最后一行开始分别做硬判决，得到：

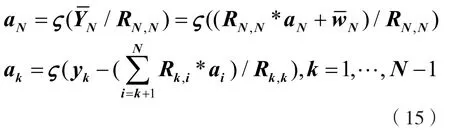
式中，y=ζ(x)表示y为距离x欧氏距离最小的整数。

由于矩阵FTN中的ISI无限长，因此构造矩阵模型时，我们需对ISI做近似截短处理。截短后长度N的值仍很大，导致DFE信号检测方法计算复杂度很高。

2.3.2PDFE信号检测方法

为有效降低计算复杂度，文献[17]提出了PDFE信号检测方法。和DFE检测算法相比，它的创新点在于：对ISI矩阵做分块处理，将ISI矩阵维度降低。先选择维度为c×c（c＜N）的分块矩阵：

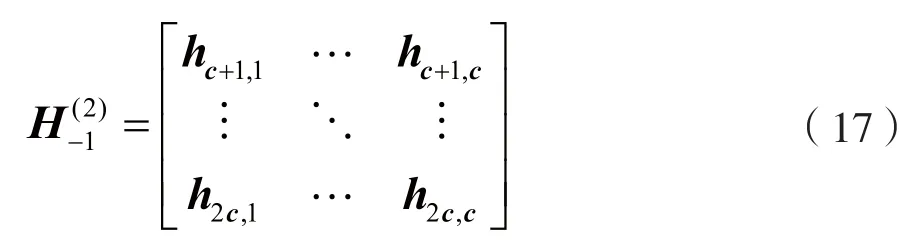
然后，选取第二个c×c分块矩阵，重复上述步骤[N/c]次即可检测出所有发送信号。第二个分块矩阵表示为：

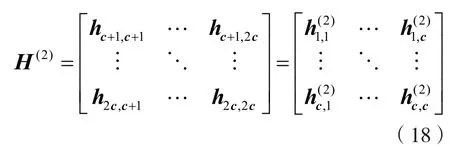
2.3.3比较与分析

（1）复杂度分析

为简化运算，只考虑复值乘法运算和ISI矩阵H的维度大小，两种信号检测方法的复杂度总结如表3所示。

表3　DFE、PDFE复杂度比较

DFE中，QR分解的复杂度正比于O(N3)，第二项和第三项分别表示左乘及硬判决。虽然PDFE相比DFE要多进行([N/c]-1)次前向干扰消除，但由于N的值远大于c，DFE中QR分解和硬判决的复杂度仍远大于PDFE，所以PDFE的复杂度优势非常明显。

（2）误码率性能分析

图8给出在AWGN信道条件下采用BPSK调制、ISI长度为L=200，升余弦滚降系数β=0.22，加速因子τ取0.9时，DFE和PDFE的误码率性能比较。

从图8中可得，当τ取值相同时，PDFE的误码率性能较DFE有所下降，原因是PDFE只考虑了部分串扰，且分块矩阵维度越小，PDFE的误码率性能越差。

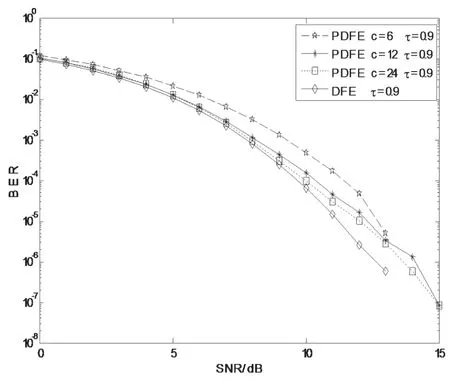
图8　DFE和PDFE误码率性能比较

3　比较与结论

为了降低接收端的复杂度，本文重点介绍了三种FTN传输系统中的低复杂度接收技术及其改进方案。加窗Chase均衡、迭代分组判决反馈均衡器（IBDFE）、判决反馈均衡（DFE）都能在一定程度上降低系统的复杂度。尤其是三种接收技术的改进算法，在保证系统误码率性能不变或降低小的前提下，明显降低了计算复杂度，为FTN系统的实用化奠定基础。表4给出以上改进型低复杂度接收方案的特点及适用范围。

表4　低复杂度接收方案对比及总结

其中，改进型WCE比加窗Chase均衡复杂度可以降低80%以上，且更适用于低信噪比的条件；LC-IBDFE在迭代次数高的情况下，复杂度优势明显；PDFE在长码间串扰情况下，对ISI矩阵分块处理后，有效降低了复杂度，所以特别适用于长码间串扰的情况。

4　结 语

如何实现FTN系统的低复杂度接收，是FTN系统面临的主要问题和挑战之一。本文从这一角度出发，重点介绍了FTN传输系统中的低复杂度接收技术及其改进方案，其中改进型WCE、低复杂度IBDFE和PDFE均为改进算法，保证了在系统误码率性能不变或降低小的条件下，能以更低的计算复杂度消除ISI，同时文章也给出了三种改进型算法的特点及适用范围。但是，本文只考虑了算法在AWGN信道条件下的性能及适用性，下一步的工作是将低复杂度接收方案向多径衰落信道推广，从而进一步推动FTN向实用化方向发展。

[1] Mazo J E.Faster-than-Nyquist Signaling[J].The Bell System Technical Journal,1975,54(08):1451-1462.

[2] LE C,SCHELLMANN M,FUHRWERK M,etal.On the Practical Benefits of Faster-than-Nyquist Signaling[C]. Vietnam:2014 International Conference on Advanced Technologies for Communications,2014:208.

[3] FORNEY G D.Maximum-likelihood Sequence Estimation of Digital Sequences in the Presence of Intersymbol Interference[J].IEEE Transaction Information Theory,1972,18(03):363-378.

[4] HAYES J F.The Viterbi Algorithm Applied to Digital Data Transmission[J].IEEE Communication Magazine, 2002,40(05):26-32.

[5] ANDERSON J B,PRLJA A,RUSEK F.New Reduced State Space BCJR Algorithms for ISI Channel[C]. Seoul Korea:International Symposium on Information Theory,2009:889-893.

[6] Prlja A,Anderson J B.Reduced-complexity Receivers for Strongly Narrowband Inter-symbol Interference Introduced by Faster-than-Nyquist Signaling[J].IEEE Transaction Communication,2012,60(09):2591-2601.

[7] CHASE D.A Class of Algorithms for Decoding Block Codes with Channel Measurement Information[J].IEEE Transaction Information Theory,1972,18(01):170-182.

[8] TANG Y S,LING S,FU F W.On the Reliability-orderbased Decoding Algorithms for Binary Linear Block Codes[J].IEEE Transaction Information Theory,2006,52(01):328-336.

[9] NAMMI S,BORAH D K.A List-based Detection Technique for Long Inter-symbol Interference Channels[J].Wireless Co mmunication,2009,8(03):1276-1283.

[10] LI H,SHEN Y H,XU K.Windowed Fast Chase Detection for Long Intersymbol Interference Channels[J].Freque nz,2010,64(07-08):134-139.

[11] SUGIURA S.Frequency-domain Equalization of Fasterthan-Nyquist Signaling[J].IEEE Wireless Communication Letters,2013,2(05):555-558.

[12] BENVENUTO N,TOMASIN S.On the Comparison Between OFDM and Single Carrier Modulation with a DFE Using a Frequency Domain Feedforward Filter[J].IEEE Transaction Communication,2002,50(04):947-955.

[13] TOMASIN S,BENVENUTO N.Fractionally Spaced Nonlinear Equalization of Faster-than-Nyquist Signals[C]. Signal Processing Conference (EUSIPCO),2014 Proceedings of the 22nd European Publication Year:2014,9(03):1861-1865.

[14] TOMASIN S,BENVENUTO N.Iterative Design and Detection of a DFE in the Frequency Domain[J].IEEE Transaction Communication,2005,53(07):1867-1875.

[15] XU Y,GUO M X,SHEN Y H,etal.A Low Complexity Iterative Frequency Domain Decision Feedback Equalization of Faster than Nyquist Signals[J].Communications Technology,2015,33(02):10-15.

[16] RINGH E.Low Complexity Algorithms for Faster-than-Nyquist Signaling:Using Coding to Avoid an NP-hard Problem[D].Sweden:Royal Institute of Technology,2013.

[17] BAEK M S,HUR N H,LIM H.Novel Interference Cancellation Technique based on Matrix Computation for FTN Communication System[C].Daejeon Korea:IEEE Military Communications Conference,2014:830-834.

张广娜（1991—），女，硕士研究生，主要研究方向为无线通信、超奈奎斯特速率传输等；

郭明喜（1978—），男，博士，讲师，主要研究方向为高速无线通信、MIMO和协同通信技术等；

沈越泓（1959—），男，博士，教授，主要研究方向为无线通信信号处理、高速数字调制技术、移动通信等。

Low-Complexity Receiver Technology in Faster-than-Nyquist Transmission System

ZHANG Guang-na, GUO Ming-xi, SHEN Yue-hong
(College of Communications Engineering,PLAUST,Nanjing Jiangsu 210007,China)

FTN signaling, with faster symbol rate than Nyquist rate, is regarded as a promising technique to improve the bandwidth efficiency. However the unavoidable ISI(inter-symbol interference) in the receiver would usually result in high complexity of the receiving device and the receiver as well. In order to offectively reduce the interference, low-complexity receiver technology and the modified algorithms are proposed, including WCE(Windows Chase Equalization) and FTN-MWCE, IBDFE (Iterative Decision Feedback Equalization) and LC-IBDFE, DFE (Decision Feedback Equalization) and PDFE(Partial Decision Feedback Equalization). The analysis on and comparison of these algorithms are done respectively from computation complexity and BER performance, and their advantages disadvantages, and applications as well also presented.

faster-than-Nyquist Signaling;ISI(inter-symbol interference);low complexity; receiver technology

National Natural Science Foundation of China (No.61301157)

TN911

A

1002-0802(2016)-08-0960-08

10.3969/j.issn.1002-0802.2016.08.002

2016-04-25;

2016-07-22

date:2016-04-25;Revised date:2016-07-22

国家自然科学基金资助项目（No.61301157）