一种无特征混沌扩频波形的设计*

姜 艳

（中国人民解放军91404部队，河北 秦皇岛 066001）

一种无特征混沌扩频波形的设计*

姜 艳

（中国人民解放军91404部队，河北 秦皇岛 066001）

混沌扩频波形具有很高的类随机性和复杂性，被广泛运用于安全保密通信领域。但是，常规的混沌波形的频谱通常是一个有色频谱，从而为敌对检测截获方提供了可利用的有效特征。因此，从混沌序列设计出发，设计了一种无特征的混沌扩频序列，并且利用该混沌扩频序列产生出一种无特征混沌扩频波形。仿真结果表明，该波形在一阶到四阶的累积量特性都与高斯白噪声保持一致，使其无法与高斯白噪声区分，从而使波形具有很好的低检测低截获特性。

混沌扩频；无特征；低检测低截获；高阶累积量

0　引 言

21世纪的战争是信息战，而通信是在信息战中取得优势的关键和灵魂。因此，保证通信安全、畅通且不被敌方检测和截获，成为了急需解决的关键技术。

近年来，人们对混沌波形进行了广泛研究。混沌波形的非周期性、宽带频谱、类似噪声的特性，使得混沌波形信号具有天然的隐蔽性。另外，混沌信号对初值的敏感特性使得混沌信号具有长期不可预测性和抗截获的能力[1-2]。因此，混沌扩频通信已成为非常有效的保密通信方式。

但是，随着信号检测技术的快速发展，出现了一些利用信号的循环相关、高阶累积量等特征的信号特征检测方法。其中，基于高阶累积量的信号检测手段由于只需要较少的先验知识且具有优越的噪声抑制能力、微弱信号检测能力，得到了广泛运用[3-4]。而常规混沌信号通常具有一个有色谱，这使得基于高阶累积量的信号检测方法能够将混沌信号与高斯白噪声区分开，从而实现对信号的检测和截获。为了提高混沌扩频波形的复杂性和低检测低截获特性，国内外学者进行了大量的研究工作。国外的哈里斯公司提出了一种基于混沌序列的无特征调制方式，使得混沌波形信号的一阶和二阶累积量与高斯白噪声保持一致[5]。国内学者宁国强、何小海等人采用两个初值的Logistic映射来产生复合混沌序列，初值空间增加了一倍，随机性更强，提高了破译的难度[6]。本文则试图利用多组混沌序列组合设计出一种具备无色谱的混沌扩频序列，进而生成无高阶累积量特征的混沌扩频波形。仿真结果表明，该波形的一阶到四阶高阶累积量特性都与高斯白噪声保持一致，从而大大提高了波形信号的低检测低截获特性，更好地保障通信的安全。

1　数字混沌扩频序列

混沌扩频序列产生方法主要有两种。一种是难以在实际中实现的混沌系统。这种混沌系统由微分方程表示，产生的是在时间上连续的混沌扩频序列。另一种是可以用数字电路来实现的混沌系统。它将差分方程转换为迭代方程来表示，产生的混沌扩频序列在时间上是离散的[7]。本文的研究是基于混沌映射方程得到混沌序列，产生的是时间上离散的混沌序列，属于第二种方法。产生原理图如图1所示。本文采用改进型的Logistic混沌映射来产生扩频伪随机序列码。

图1　数字混沌序列产生原理

初始值经映射方程迭代后成为实值混沌序列，然后通过数值化将实值序列量化为二进制的时间离散混沌数字序列。

改进型的Logistic映射定义式为：

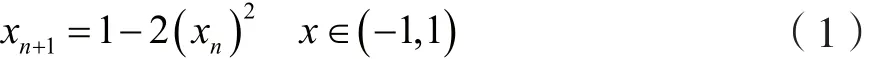
此时，改进型Logistic映射的概率密度函数为：

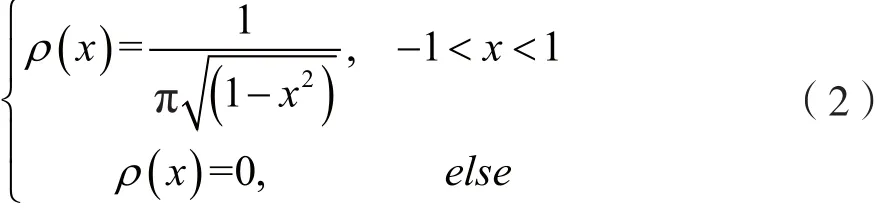
（1）均值

改进型Logistic映射序列的均值为：

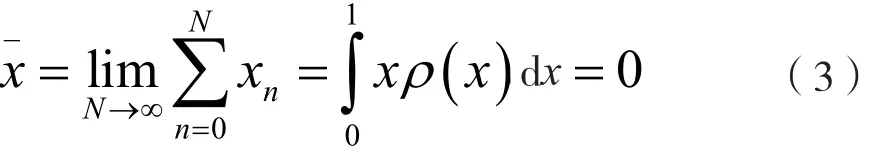
（2）自相关性

当时间间隔τ=0时，有：

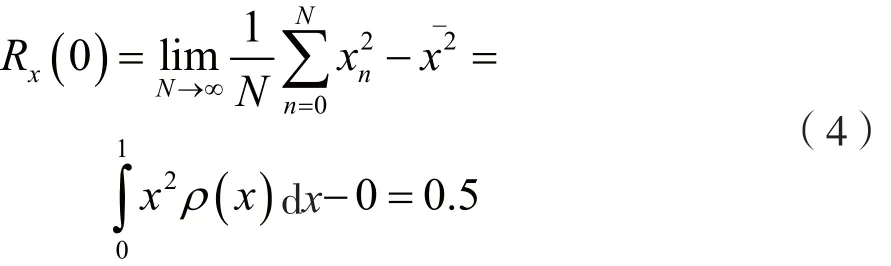
当时间间隔τ≠0时，有：

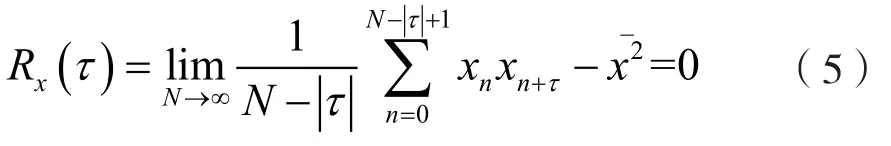
当混沌序列长度N=1 000时，混沌序列的自相关特性如图2所示。

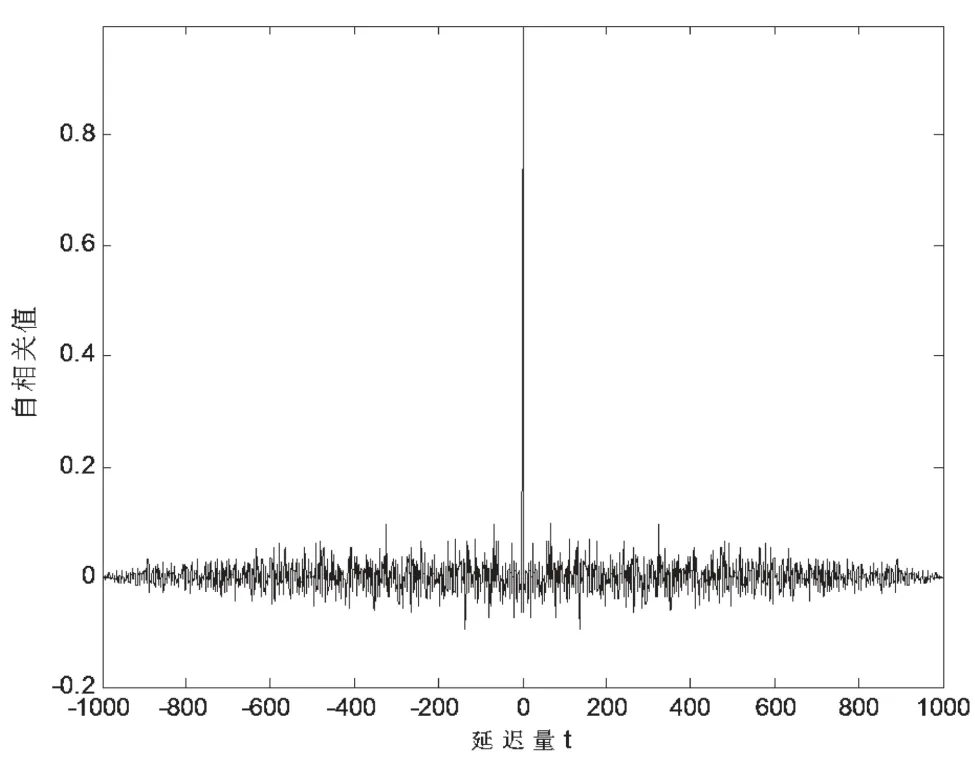
图2　改进型Logistic映射序列的自相关特性

（3）互相关性

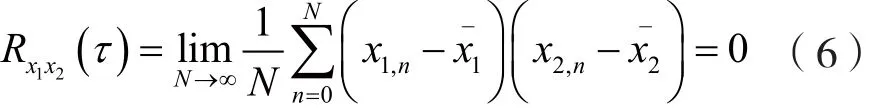
当混沌序列长度N=1 000时，混沌序列的互相关特性如图3所示。

图3　改进型Logistic映射序列的互相关特性

从上面的分析可以看出，改进型Logistic映射均值为零，自相关接近于δ函数，互相关几乎为零，其一阶和二阶累积量特性等同于零均值白噪声，具有良好的随机性、相关性、复杂性。这种序列难于重构和预测，从而使检测和截获分析者难以破译，因而非常适合于低检测低截获通信设计。

2　一种无特征混沌扩频序列

由于波形信号存在如PSK、QAM等调制方式，而这些调制方式都会存在一些特征。基于高阶累积量的检测手段能够利用这些特征实现对信号的检测和截获。因此，本文对具有随机性和高阶累积量与高斯白噪声无法区分的无特征序列展开研究。目前，采用的混沌扩频序列多是基于单一的混沌映射进行设计和分析。而随着对混沌理论的进一步深入研究和广泛应用发现，单一的混沌映射产生的序列生成简单，但随机性能和高阶累积量特性有限。本文给出了采用多个不同初值的Logistic映射来产生复合型混沌序列，使得混沌序列的随机性更强，在高阶累积量特性上无限接近高斯白噪声。同时，给出复合型Logistic映射组数与高斯累积量特性的关系图。复合型混沌序列原理如图4所示。

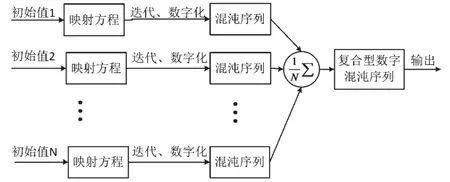
图4　复合型无特征混沌序列生成原理

原理图中，映射方程统一使用前文提出的改进型的Logistic映射。数字化量化时通常有两种方法，分别为“十进制转二进制法”和“门限值法”。其中门限法可以提高效率，降低计算量，但是采用这种方法通过二进制转十进制的方式反向得到原数字，存在很大的破译风险。所以，本文的所有仿真分析中，数字化时都选择传统的“门限值法”[8-9]。

改进型的Logistic映射序列在一阶和二阶累积量上具备了高斯特性，本文目的是设计一种能够抵抗高阶累积量的混沌序列。为了得到满足本文设计要求的复合型混沌序列，使得混沌序列在高阶累积量特性上与高斯白噪声保持一致，从而保持和加强抵抗高阶累积量检测的能力。因此，本文对映射组数N与累积量特性的关系进行了研究，并与高斯白噪声的性质进行对比。

为了更好地说明复合型混沌序列的映射复合组数与高阶累积量特性的关系，本文对一阶到四阶累积量（均值、方差、偏度、峭度）进行分析，结果依次如图5、图6、图7和图8所示。

图5　映射复合组数N与均值的关系

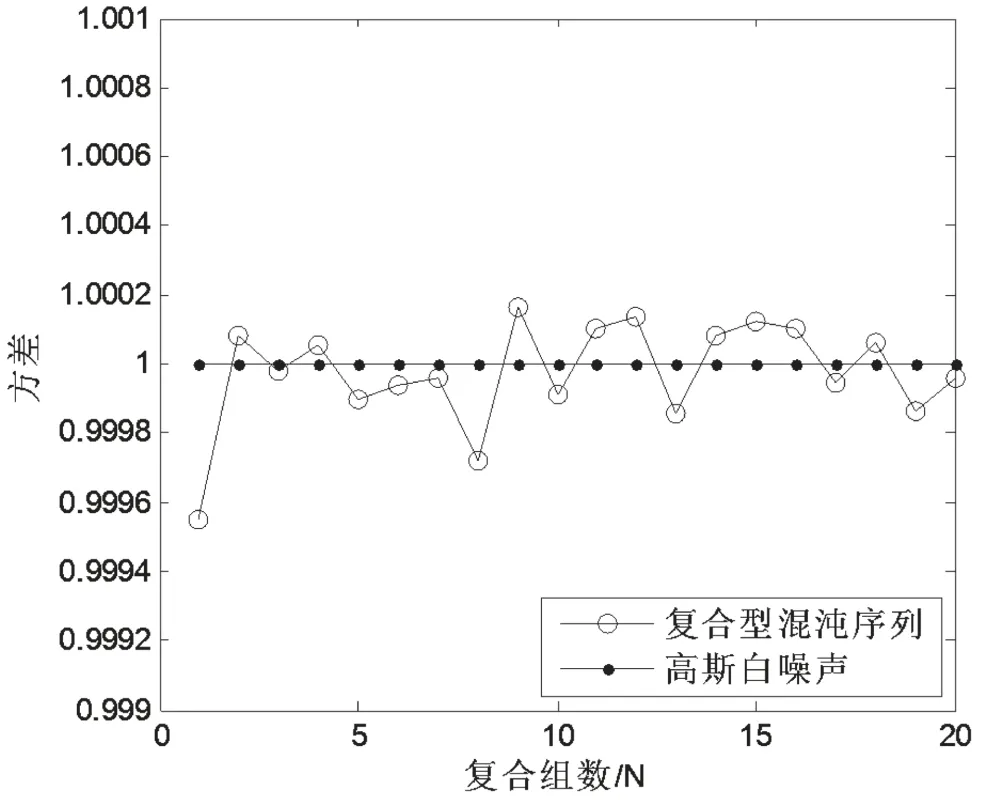
图6　映射复合组数N与方差的关系

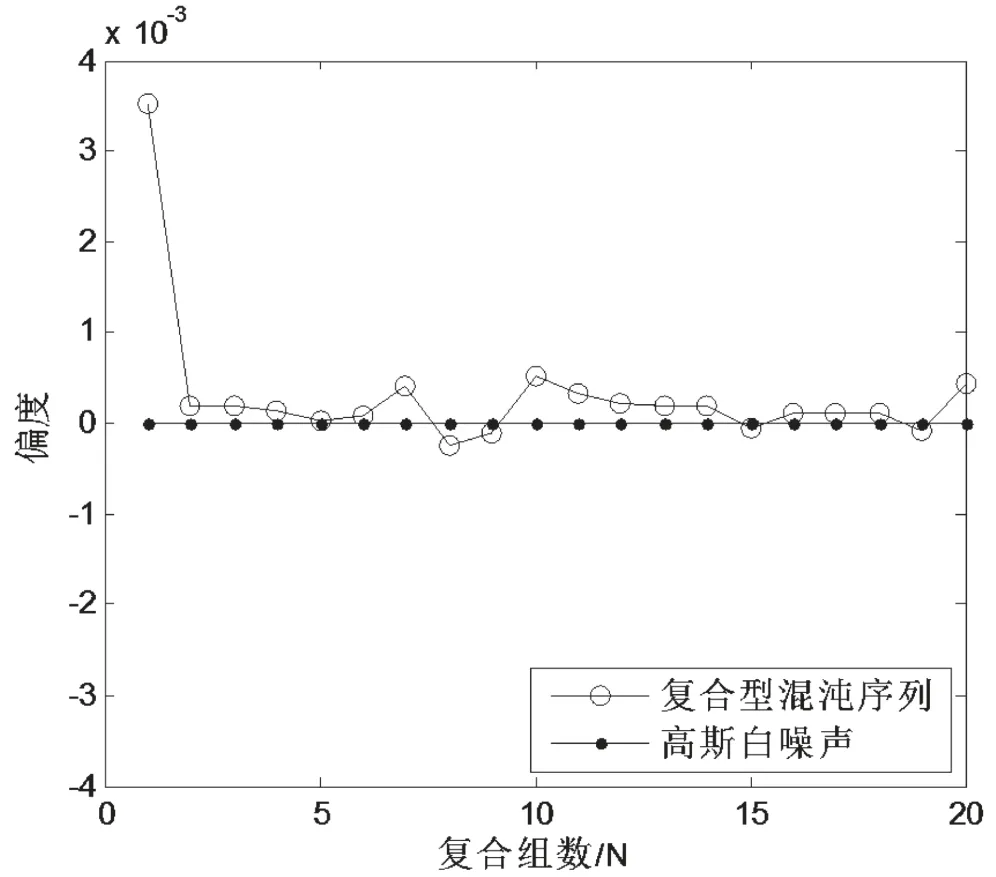
图7　映射复合组数N与偏度的关系

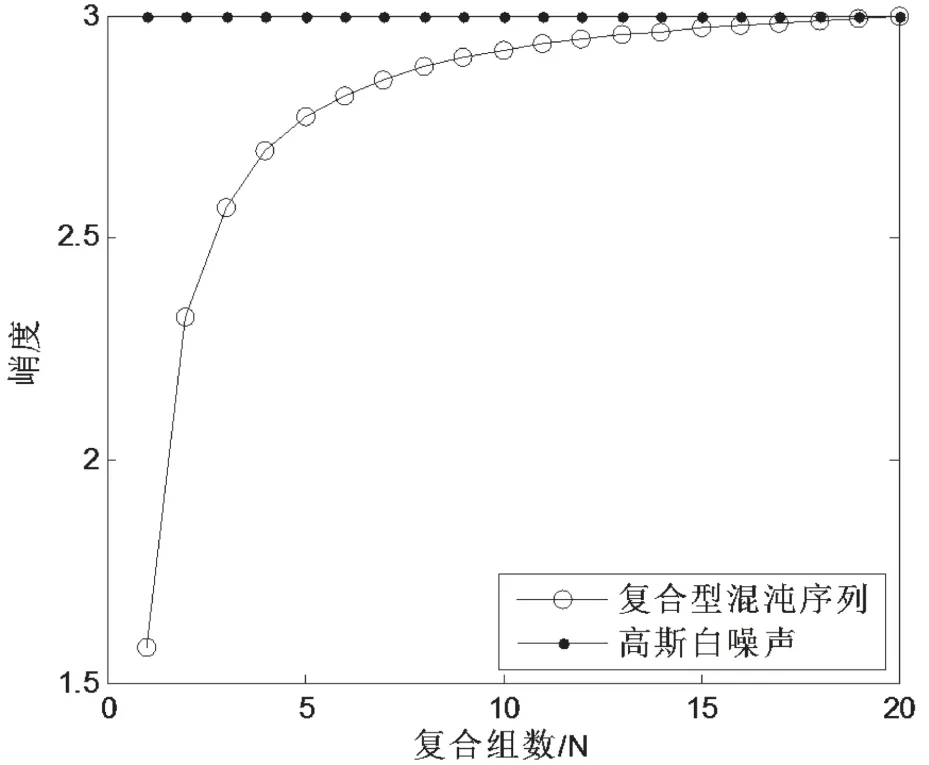
图8　映射复合组数N与峭度的关系

通过上面映射复合组数N与各阶累积量量的关系图可以看出，当复合组数N=20时，复合型混沌序列在一阶到四阶的累积量都与高斯白噪声的累积量特性非常接近，从而使得混沌序列与高斯白噪声无法被区分。

经过无特征设计后的混沌序列依然具有很好的均值、自相关特性和互相关特性。

（1）均值

（2）自相关性

当时间间隔τ=0时，有：

当时间间隔τ≠0时，有：

虽然到目前为止我国“人大” 已经颁布了许多有关经济犯罪方面的法律，但却没有一个专门针对会计故意性信息失真的法律，建议“人大”将会计故意性信息失真犯罪列入我国的《刑法》中。同时，我国应加紧制定《会计法》的处罚条例和实施细则，具体规定违法处罚的定性标准，提高会计违法成本，以改变目前《会计法》难以执行的情况。一方面广泛地吸收实业界、学术界和政府各方面意见，实现会计准则的公平、公正，适应经济发展的需要。另一方面要加快会计准则制定的速度，及时出台与国际接轨的准则和制度，使之适应会计实践的发展。

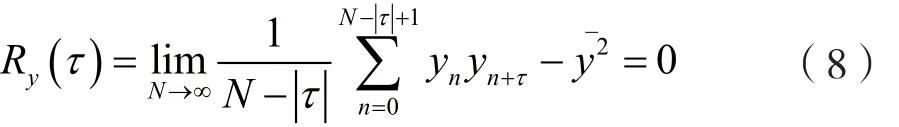
当混沌序列长度N=1 000时，混沌序列的自相关特性如图9所示。

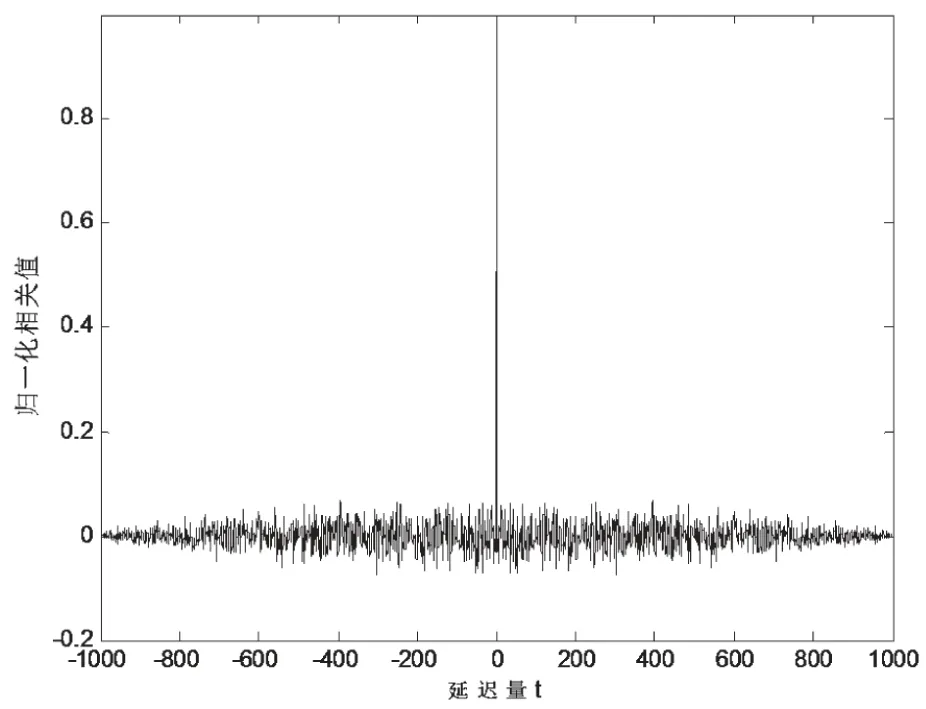
图9　复合型无特征混沌序列的自相关特性

（3）互相关性

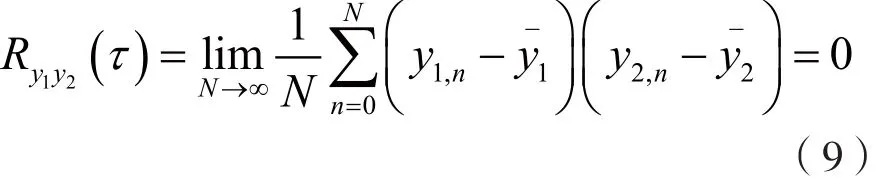
当混沌序列长度N=1 000时，混沌序列的互相关特性如图10所示。

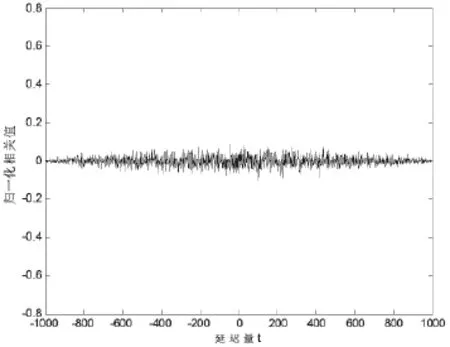
图10　无特征混沌序列的互相关特性

根据前面的分析，本文设计的复合型的无特征数字混沌序列在高阶累积量（一阶到四阶）特性上与高斯白噪声保持一致，因此使得基于高阶累积量的检测手段无法与高斯白噪声区分开来.同时，该无特征混沌序列保持着原本混沌序列良好的自相关性和互相关性，因此可以很好地适用于扩频通信中。

3　无特征混沌扩频波形的设计

针对前面方差不恒定这一问题，本文试图通过增加一组辅助信息流来使得信号大小恒定。本文给出一种利用辅助数据来实现无特征混沌扩频波形的设计方案，使得扩频后的信号完全无法通过高阶累积量进行区分，设计原理图如图11所示。

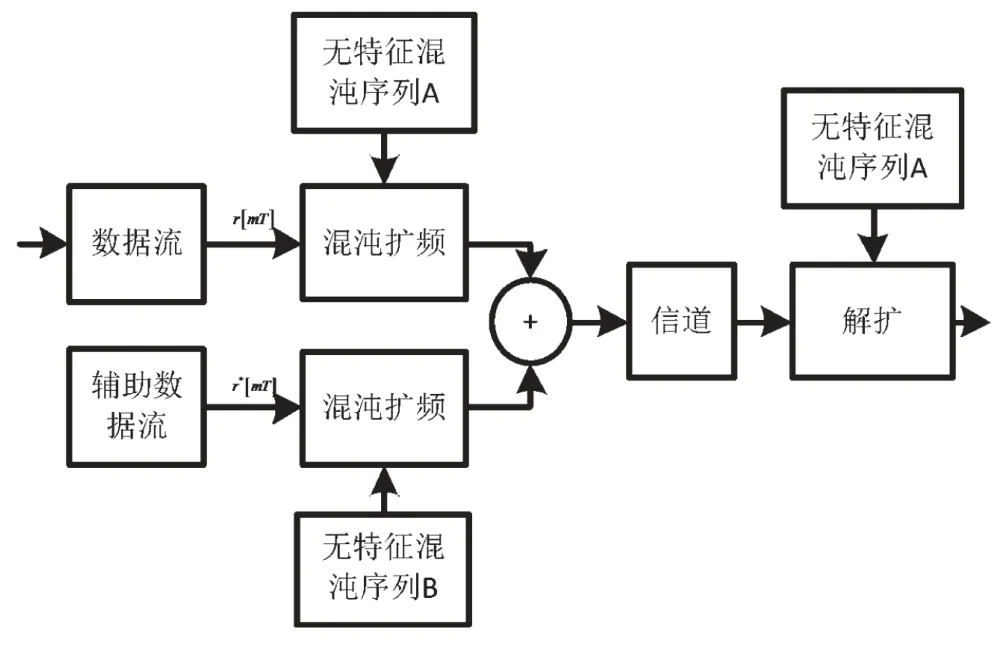
图11　无特征混沌扩频波形原理

与上面分析相似，可以将经过频域扩频处理后的信号表示为：

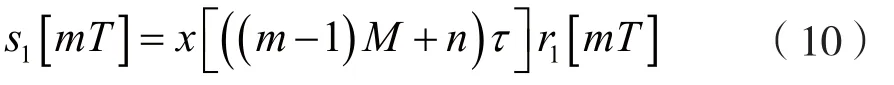
式中，T表示符号周期，τ表示码片间隔，x表示混沌扩频序列A，r1[mT]表示频域扩频处理后的符号。此外，这里的r1[mT]是经过归一化处理的，

而辅助数据流与频域扩频后的数据流具有相似形式，表示为：

因此，现在信号的表达为：

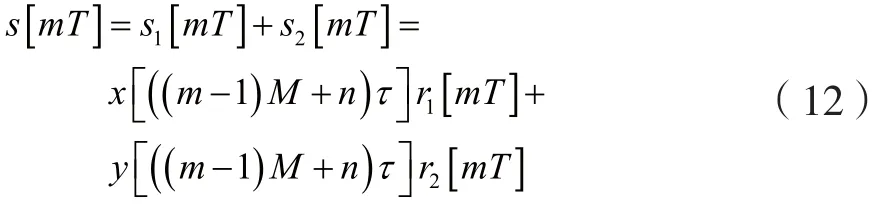
下面对现在信号的高阶累积量特征进行理论分析。

均值特性：

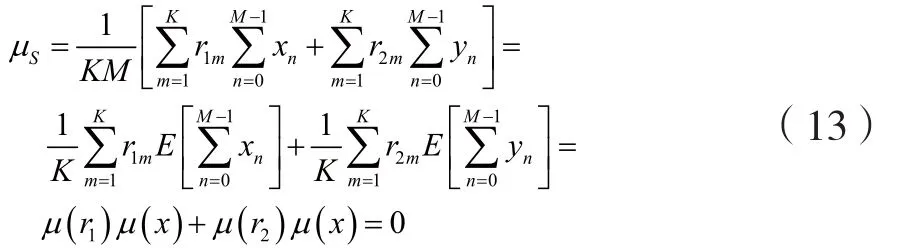
方差特性：

因为，混沌序列x和混沌序列y为不同的混沌序列，互相关值为零，因此有且故：

偏度特性：

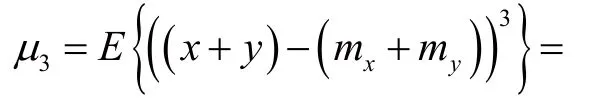
峭度特性：

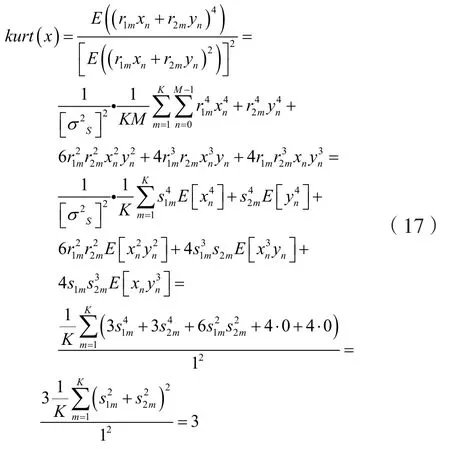
从上面的理论分析推导过程中可以看出，只要混沌序列长度满足一定条件，经过混沌扩频后的信号的一阶到四阶累积量特征就全部和高斯白噪声保持一致，并且不会随着信号大小的变化而变化。

4　实验结果分析

为了证明本文设计的混沌扩频波形，本文对所设计的混沌扩频波形的高斯累积量进行仿真实验。本文采用的是复合组数为20的混沌扩频序列，长度为1 000，仿真实验次数为1 000次。实验结果与标准正态分布的高斯信号进行对比，结果如表1所示。

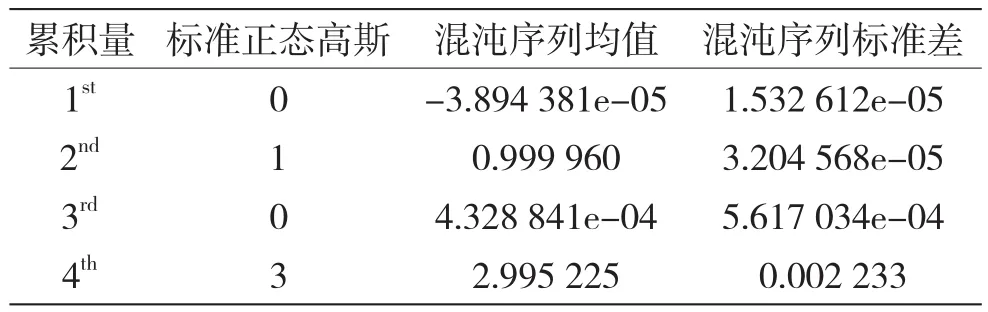
表1　无特征混沌波形与标准正态的高阶累积量对比

从上面的实验结果可以看出，经过混沌扩频后的信号的一阶到四阶累积量特征已经全部和高斯白噪声保持一致，并且不会随着信号大小的变化而变化。因此基于高阶累积量的检测手段将失去对我方波形的检测能力，从而使得无特征混沌扩频后的波形具备了完美的抗高阶累积量检测法的能力。

5　结 语

本文首先对常规的改进型Logistic映射的数字混沌序列进行研究，分析序列的自相关、互相关特性。其次，在此基础上，提出一种通过多组常规混沌序列复合产生的一种新型的无特征混沌序列，并对复合组数与混沌序列的累积量特性关系进行详细分析，从而构造出一种合适的无特征混沌序列。再次，本文在无特征混沌序列的基础上设计出一种无特征混沌扩频波形，并对该波形的高阶累积量特征进行了理论上的推导和分析，证明了该混沌波形与混沌序列的高阶累积量特征保持一致。最后，通过仿真实验证明，本文设计的无特征混沌扩频波形具备完美的高阶累积量特性，使得检测手段无法将之与高斯白噪声区分，从而大大提高了波形的低检测、低截获特性和安全性。

[1] 姚明海.混沌系统的控制与同步及其在保密通信中的应用[D].杭州:浙江工业大学,2005. YAO Ming-hai.Control and Synchronization of Chaotic System and Its Application in Secure Communication[D]. Hangzhou:Zhejiang University of Technology,2005.

[2] Chong F U.A Fast Chaotic Spread Spectrum Communication System and Its Performance Analysis[C].2005 Global Mobile Congress-Papers,2005:237-242.

[3] Amblard P O,Brassier J M.Adaptive Estimation of the Fourth-order Cumulant of a White Stochastic Process[J]. Signal Processing,1995,42(03):37-43.

[4] 张廷华,樊桂花.基于四阶累积量的微弱激光回波信号检测[J].科学技术与工程,2010,10(22):5381-5384. ZHANG Ting-hua,FAN Gui-hua.Faint Echo Signal Detection Based On Fourth-Order Cumulant[J].Science Technology and Engineer-ing,2010,10(22):5381-5384.

[5] Michaels A,Chester D.Featureless Chaotic Spread Spectrum Modulation of Arbitrary Data Constellations[J].2011 IEEE 12th International Workshop on Signal Processing Advances in Wireless Communications,2011:36-40.

[6] 宁国强,何小海,侯波等.一种新的混沌扩频序列的研究与应用[J].四川大学学报:自然科学版,2009,46(05):1341-1346. NING Guo-qiang,HE Xiao-hai,HOU Bo,et al.Research and Application of a New Chaotic Spread Spectrum Sequence [J].Journal of Sichuan University:Natural Science Edition,2009,46(05):1341-1346.

[7] Chester D B,Michaels A J.Digital Generation of a Chaotic Numerical Sequence[C]. U.S. Patent Pending, 2011.

[8] An C,Zhou T.A Method of Generating Chaotic Spread Spectrum Sequences based on Multilevel Quantification[C]. International Conference on Acoustics,2003(04):165-168.

[9] 俞斌.改进的混沌扩频序列的产生及其应用研究[D].长沙:湖南大学,2012. YU Bin.Study on the Generation and Application of the Improved Chaotic Spread Spectrum Sequence[D]. Changsha: Hunan University,2012.

姜 艳（1969—），女，硕士，高级工程师，主要研究方向为通信与通信对抗技术。

A Featureless Chaotic Spread Spectrum Waveform

JIANG Yan
（PLA Unit 91404,Qinhuangdao Hebei 066001,China）

The chaotic spread spectrum waveform ,as with high randomness and complexity, is widely applied in the fields of security and private communication. However the conventional chaotic waveform usually exhibits colored spectra, thus providing discernible features for the advisary to detect and acquire the transmitted data. The characteristic of chaotic sequence is discussed, and a featureless chaotic spread spectrum sequence designed. And based on the featureless chaotic sequence, a featureless chaotic spread spectrum waveform is generated. Simulation analysis indicates that, all cumulant from the first order up the fourth order of waveform is consistent with the White Gaussian noise, no difference with the White Gaussian noise, so the featureless chaotic spread spectrum waveform has fairly low detection probability and interception probability.

chaotic spreading spectrum; featureless; LPI/LPD；high order cumulant

TN914.42

A

1002-0802(2016)-08-0986-06

10.3969/j.issn.1002-0802.2016.08.006

2016-04-19;

2016-07-18

date:2016-04-19;Revised date:2016-07-18