需求和零售商费用同时变化且信息不对称下的供应链协调应对

姚泽有， 曹细玉

(1.电子科技大学 中山学院 管理学院， 广东 中山 528402;2.电子科技大学 中山学院 经贸学院， 广东 中山 528402)



需求和零售商费用同时变化且信息不对称下的供应链协调应对

姚泽有1， 曹细玉2*

(1.电子科技大学 中山学院 管理学院， 广东 中山 528402;2.电子科技大学 中山学院 经贸学院， 广东 中山 528402)

考虑一个二级供应链，它是由单个制造商和单个零售商组成，在随机市场需求下分析了供应链在数量折扣契约下的协调性；然后，探讨了随机市场需求和零售商费用在突发事件下同时发生变化且信息不对称时供应链在数量折扣契约下的协调性，研究结果表明：基准的数量折扣契约在突发事件下不能使供应链协调，由此给出了供应链应对突发事件的最优应对策略，并对原来的数量折扣契约进行了调整使其具有抗突发事件性.最后，通过数值计算得到了正常情况下供应链的最优订货量和供应链收益，并通过对新旧数量折扣契约在突发事件下订货量和供应链收益的比较分析，进而对结论的有效性进行了验证.

突发事件； 信息不对称； 数量折扣契约； 供应链协调

进入21世纪以来，突发事件(如911恐怖事件、SARS、地震、雪灾、全球金融危机等)的频繁发生，使人们突然意识到人类正处在一个突发事件频繁发生的社会时期.在经济全球化和企业国际化的背景下，突发事件发生所造成的破坏力和影响范围不但没有消弱，反而得到不同程度的扩张和强化，如何进行突发事件应急管理成为社会各界关注焦点[1-2].突发事件将对供应链系统运作的稳定与协调产生巨大影响，例如导致需求市场波动、供应中断或延迟、生产成本或销售成本突变、信息通道堵塞、运输系统中断等，使得供应链协调失效.由此可见，如何使供应链系统应对突发事件的研究显得十分重要[3].关于这方面的研究思想起源于Thengvall和Yu等人在航空应急管理方面的探索[4-5]；当突发事件引起市场需求波动时，关于供应链以数量折扣契约来应对的策略，Qi等进行了研究[6]；于辉等认为：突发事件引起随机市场需求波动时，可以分别利用回购契约和批发价格契约来应对并实现供应链的协调[7-8]；王艳和高修成研究了零售商竞争下生产费用扰动的供应链协调[9]；吴忠和等人运用期权契约研究了需求和生产成本同时变化的供应链协调应对[10]；曹二保和赖明勇研究了n个竞争零售商下生产成本和需求同时发生突变时借助收益共享契约来应对突发事件达到供应链协调的策略[11].这些学者所进行的研究并没有考虑突发事件下变动要素信息不对称的情况，而且有关这方面的研究文献也非常少.Zhuang和Zhao研究了突发事件下零售商成本变化且信息不对称时的供应链协调问题[12-13]；庞庆华等研究了需求依赖于价格的三阶段供应链在突发事件下需求发生变化时的供应链协调应对问题[14]；盛方正等对突发事件引起零售商订单拖欠的供应链协调问题，分别基于订单拖欠成本信息对称与否两种情况进行了研究[15]；吴忠和等研究了突发事件下零售商成本信息不对称下的供应链协调机制问题[16].但从现有的文献看，这些学者的研究主要针对突发事件下确定型市场需求的多因素变化，或者突发事件下随机市场需求的单因素变化，对随机市场需求及双因素变动而且信息不对称的复杂情形还需作进一步的深入探索.

因此，本文对此问题进行研究以期寻找零售商费用以及随机市场需求在突发事件下同时变化且信息不对称的供应链协调应对策略，将为突发事件下多因素同时变化且是信息不对称的供应链协调应对提供研究思路和方法.

1 数量折扣契约基准模型

设T(Q，w)=wQ为制造商给予零售商的转移支付，则零售商、制造商和供应链的期望收益分别为

πr=pS(Q)+sI(Q)-hL(Q)-λQ-T(Q，w)=

(p+h-s)S(Q)-(w+λ-s)Q-hμ，

(1)

πm=T(Q，w)-cQ=(w-c)Q，

(2)πc=πr+πm=(p+h-s)S(Q)-(c+λ-s)Q-hμ.

(3)

供应链系统在数量折扣契约下要实现协调，就要确定合理的转移支付使T(w，Q)能使供应链协调.

因为F(x)是严格递增的，从式(3)可得πc是严格凹的，因而最优订货量Q*是唯一的.对比式(1)和(3)，可知若供应链要实现协调，则在转移支付T(w，Q)中，批发价格w还要满足：对于任意β(0〈β〈1)，有

(1-β)(c+λ-s)+c，

这样零售商的期望收益为

πr=(p+h-s)S(Q)-(w-s)Q-hμ=

β(p+h-s)S(Q)-β(c+λ-s)Q-hμ=

βπc-(1-β)hμ.

显而易见，在数量折扣契约T(w，Q)下零售商的期望收益为供应链期望收益的放射函数，供应链能够实现协调.

2 突发事件对供应链的影响分析

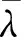
πrG=(p+h-s)SG(Q)-

(4)

πmG=(w-c)Q-k1(Q-Q*)+-k2(Q*-Q)+，

(5)

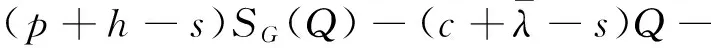
hμG-k1(Q-Q*)+-k2(Q*-Q)+.

(6)

hμG-k2(Q*-Q)，

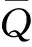
定理1当市场需求和零售商费用在突发事件下同时变化时，则供应链此时的最优订货量为

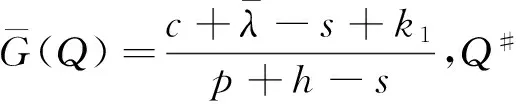
hμG-k1(Q-Q*)，

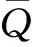
hμG-k2(Q*-Q)，

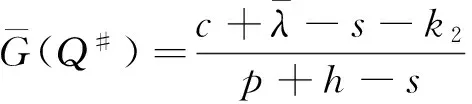
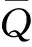
故可知当市场需求和零售商费用在突发事件下同时变化时，此时供应链最优订货量为：

定理2当市场需求和零售商费用在突发事件下同时变化且信息不对称时，如果需求和零售商费用有较大变化且仍采取原数量折扣契约T(w，Q)，则供应链的协调性将失效.

证明当市场需求和零售商费用在突发事件下同时变化且信息不对称时，如采用原数量折扣契约T(w，Q)，此时零售商的期望收益为：

πrG=(p+h-s)SG(Q)-

k2(Q*-Q)+]-(1-β)huG.

(7)

3 供应链在突发事件下的协调应对

定理3供应链可在新的数量折扣契约T(wanti，Q)下实现对突发事件的协调应对，这里

k1min[1，(Q-Q*)+]-k2min[1，(Q*-Q)+].

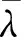
πrG=(p+h-s)SG(Q)-

(8)

制造商在获得需求信息后，就可确定能够实现收益最大化的最优数量折扣价格弹性系数θ.此时，其期望收益为

(9)

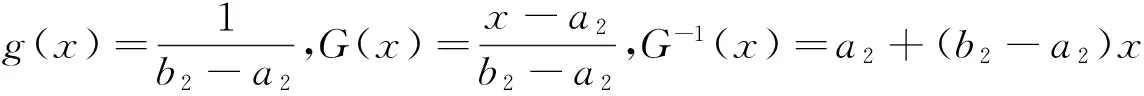
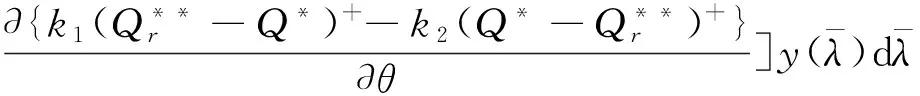
(10)

如果突发事件造成市场需求变大，则由引理1可得式(10)为

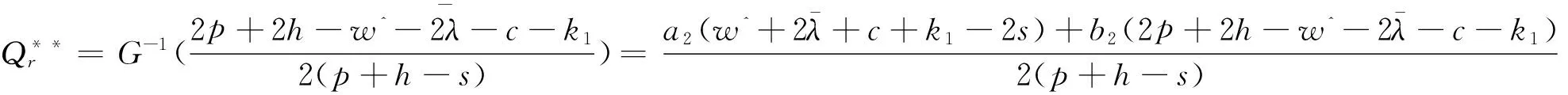
(11)

如果突发事件造成市场需求变小，则由引理1可得式(10)为

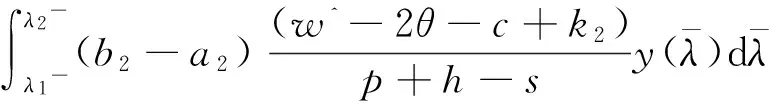
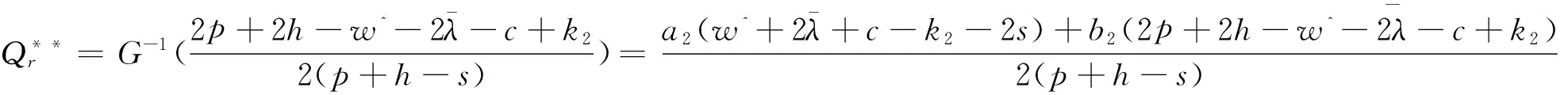
(12)

另一方面，突发事件发生后零售商费用也是零售商的隐匿信息，依据Myerson的显示原理[18]可设计一个最优机制让零售商对其费用说实话，此时制造商的优化问题可转化为

(13)

(14)

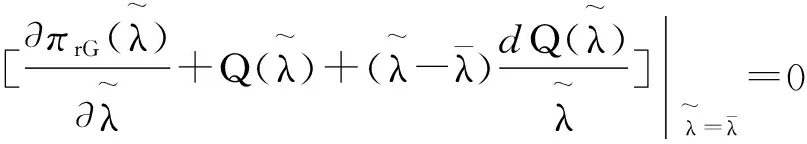
(16)

由式(16)得到

(17)

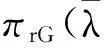
(18)

当突发事件导致市场需求增大时，式(18)变为

(19)

(20)

当市场需求在突发事件下减小时，式(18)变为

(21)

(22)

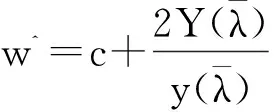
4 数值试验

设某区域对某种产品的市场需求，在正常情况下是区间[1000，1500]上的均匀分布，制造商制造单位产品的成本为c=10，产品的单位售价p=20，零售商每销售一个单位商品的费用λ=2.5，因缺货而造成的零售商单位商品机会损失h=2，因商品没有在销售季节结束时全部售出而形成商品剩余，其单位残值s=3，由制造商分担的处理费用k1=1.2，k2=2.2.则当β=0.4时，对整条供应链而言，最优订货量Q*=1250，转移支付w(Q*)=15.13，收益πc(Q*)=8187.5.

5 结语

通过市场需求和零售商费用在突发事件下同时发生变化且信息不对称时供应链的协调应对研究，可知当市场需求变化不大时，供应链协调仍可在原应对策略即原数量折扣契约下实现；而当市场需求变化较大时，供应链在原数量折扣契约并不能实现协调，但供应链在新的数量折扣契约可协调应对突发事件，而且具有抗突发事件性.但是，该研究仅仅只是二级供应链节点成员只有单个而且是单个周期下的协调应对问题，事实上在现实中，一是供应链会有更为复杂的网络结构，如供应链同一节点有多个竞争者或多级供应链等更为复杂网络结构；二是更多的因素可能因突发事件而发生变化，如生产成本、销售费用和市场需求3者在突发事件下同时变化且信息不对称；三是后续周期的生产和销售计划也可能受到突发事件的影响，由此可见，考虑多周期内更为复杂的供应链网络结构或更多因素变化且信息不对称下利用数量折扣契约来协调应对突发事件是下一步要研究的内容.

[1] DEBRA E， ROBERT B， HANDFIELD J B.Ways to guard against disruption[J].Supply Chain Management Review， 2005， 1(1):46-53.

[2] KLENDORFER P R，SAAD G H. Managing disruption risks in supply chain[J].Production and Operations Management， 2005， 14(1):53-688.

[3] 于 辉， 陈 剑， 于 刚. 协调供应链如何应对突发事件[J]. 系统工程理论与实践， 2005， 25(9):9-16．

[4] THENGVALL B， BARD J F， YU G. Balancing user preferences for aircraft recovery during airline irregular operations[J]. IIE Transactions， 2000， 32(3):181-193.

[5] YU G， YANG J. Optimization application in the airline industry[C]//Du D Z, PARDOLOS P M. Handbook of Combinational Optimization, kluwer Norwell, MA, 2003.

[6] QI X T，BARD J，Yu G. Supply chain coordination with demand disruptions [J]. Omega，2004， 32(4):301-312.

[7] 于 辉， 陈 剑， 于 刚. 回购契约下供应链对突发事件的协调应对[J].系统工程理论与实践， 2005， 25(8):38-43.

[8] 于 辉， 陈 剑， 于 刚. 批发价格契约下的供应链应对突发事件[J].系统工程理论与实践， 2006， 26(8):33-41．

[9] 王 艳， 高修成. 一种带有生产费用变化的供应链协调问题[J].数学杂志， 2005， 25(5):583-590.

[10] 吴忠和， 陈 宏， 赵 千. 需求和生产成本同时扰动下供应链期权契约应对突发事件[J].中国管理科学， 2013， 21(4):98-104.

[11] 曹二保， 赖明勇. 需求和成本同时变化时多零售商供应链协调[J].系统工程理论与实践， 2010， 30(10):1754-1761.

[12] ZHUANG P， ZHAO L D. Supply chain coordination mechanisms under asymmetric information with retailer cost disruptions[J]. Journal of Southeast University (English Edition)， 2007， 23(4):620-625.

[13] ZHUANG P， ZHAO L D. Coordinating pricing strategies in supply chain under asymmetric information and disruptions[J]. Journal of Southeast University (English Edition)， 2007， 23(12): 15-22.

[14] 盛方正， 季建华， 周 娜. 信息不对称时发生突发事件供应链的协调[J].工业工程与管理， 2008， 13(4):6-10.

[15] 庞庆华， 张 月， 胡玉露， 等. 突发事件下需求依赖价格的三级供应链收益共享契约[J].系统管理学报， 2015， 24(6):887-896.

[16] 吴忠和， 陈 宏， 吴晓志， 等. 突发事件下不对称信息供应链协调机制研究[J].运筹与管理， 2015， 24(1):48-56.

[17] Ross S M. Stochastic Processes[M].New York: John Wiley&Sons，1996．

[18] MYERSON R B.Optimal auction design[J].Mathematics Operations Research， 1981， 6(1): 58-73.

Supply chain coordination under demand and retailer costs disruptions along with asymmetric Information

YAO Zeyou1， CAO Xiyu2

(1.Management School， Zhongshan College， University of Electronic Science and Technology，Zhongshan，Guangdong 528402；2.School of Economics and Commerce， Zhongshan College，University of Electronic Science and Technology， Zhongshan，Guangdong 528402)

Taking a supply chain consisting of one manufacturer and one retailer as object， the coordination function with quantity discount contract was analyzed under the stochastic market demand. Then， the above coordination was studied on asymmetric information and simultaneously disruption of market demand and retailer’s cost under emergency. The results show that the disruption will broke this supply chain coordination. Thus， an optimal strategy for the supply chain to deal with the disruptions is proposed has and the formal quantity discount contract is adjusted for its anti-disruption ability. Additionally， the optimal order quantity and supply chain profit is generated by numerical calculation under normal circumstances. Furthermore， difference between the formal and the optimal order quantity and supply chain profit is analyzed to verify the effectiveness of the above conclusion．

emergency； asymmetric information； quantity discount contract； supply chain coordination

2015-09-20.

广东省自然科学基金项目(2014A030313644);电子科技大学中山学院科研团队培育基金项目(411YT01).

1000-1190(2016)02-0314-07

F406.2

A

*通讯联系人. E-mail: kejian200609@163.com.