基于地理加权主成分的经济发展综合评价研究——以江苏省为例

马志飞， 李在军， 张雅倩， 吴启焰

(南京师范大学 地理科学学院， 南京 210023)



基于地理加权主成分的经济发展综合评价研究
——以江苏省为例

马志飞， 李在军， 张雅倩， 吴启焰*

(南京师范大学 地理科学学院， 南京 210023)

地理加权主成分分析可判别各主成分的方差贡献的空间变动，并诊断出影响各主成分空间变化的变量.本文在结合传统主成分分析与地理加权主成分分析技术，选取经济发展水平综合评价指标，对江苏省63个县、市的经济特征进行主因子提取.得到以下主要结论：主成分分析提取得到3个主成分，分别表征经济增长方式、经济结构与经济动力；蒙特卡罗检验在0.05水平下，显著性拒绝主成分的特征值与因子载荷在空间变化上的平稳性假设；地理加权主成分的因子载荷主导着不同地区的经济结构特征，且呈集中连片分布特性，地理加权主成分的方差贡献率存在着明显的南北分异态势.可见，地理加权主成分分析可以有效识别各主成分的局域空间变化效应，诊断出影响地区经济特征空间变化的主要变量，有利于深化对社会经济要素空间的分异特征和内在机理的认知与理解.

经济发展综合评价； 主成分分析； 地理加权主成分分析； 江苏省

区域经济系统是多要素(变量)共同影响作用的结果，呈现出迥异的空间格局特征[1].主成分分析技术作为一种传统而古老的综合评价方法，被广泛应用于自然与社会科学多要素交互影响研究[2-3]，通过对多元评价指标进行降维处理，提取具有代表性的主成分，并进行合理解释与分析，从而可以有效的识别多维数据内部结构的基本特征，适合地区经济发展的综合评价研究.

而传统的主成分分析方法假设数据矩阵协方差结构在空间变化上是恒定的，尽管各样本的主成分得分在空间分布上具有显著的变动，但其内在的特征值与因子载荷在空间上并未变化，故其忽略了主因子载荷向量与方差贡献的空间变化，是一种建基于全局的统计分析方法[4-10].而世界并非一成不变的均质空间，而是交织着波动与变化，由于空间异质性、空间非平稳性及空间相关性的存在，使得地区单元并不孤立的存在，而是双向或多向的相互影响、相互作用[11-14]，因此，主成分分析对空间数据变化的解释呈现有偏的结构特征，不能反映出地理单元综合评价的空间变化特性，且忽略了地区特性的空间交互效应.

伴随着空间数据分析技术的成熟与完善，社会经济现象的空间异质性与空间相关性现象被广泛揭示，空间变化成因机制的解释也日趋完善，空间误差回归、空间自相关回归、地理加权回归与空间面板回归模型得以广泛应用[15-18].尤其是地理加权回归分析技术的应用与推广，使得社会经济现象空间异质性的解释得到极大提高，而地理加权回归分析不能处理多元变量的共线性.因此，将传统主成分分析技术推广到空间分析的层面，引起了学者的广泛关注，非空间的主成分分析技术逐渐被扩展到地理加权主成分分析[19-22].地理加权主成分分析技术可以帮助了解社会经济现象地理变化的结构特征，识别空间变化主成分的最大因子载荷变量，并可对主成分方差贡献率的局部空间分布特征进行可视化，优化地理加权回归变量选择，不仅可以弥补主成分分析的不足，而且增强了社会经济地理分异现象的分析与解释.

地理加权主成分分析对人口结构特征与土壤特性的解释具有明显的优势[10，23]，详细的解释了多元变量间的空间变化关系，可以清晰的识别各主成分因子载荷的空间变化特性.而现有综合社会经济特征评价的研究仅仅停留在传统主成分分析的层面，并未考虑到主成分的空间变化，这在一定程度上限制了对社会经济空间分异特征的认识与解释.基于此，本文探索性地采用了地理加权主成分分析对江苏省各县、市的综合经济特征进行评价研究，探索经济特性的空间变化特征，首先利用主成分分析技术对地区经济特性进行主成分提取，然后采用地理加权主成分分析诊断影响地区经济特征空间变化的主要变量，捕捉经济特性的地理分异特征.

1 数据来源与研究方法

1.1 数据来源

地区经济发展的综合评价涉及经济结构、经济实力、经济外向型、经济发展动力等多方面，本文以2010年江苏省63个县、市作为基本研究单元，在参照综合经济发展综合评价研究的基础上[24-26]，在数据可获得性的原则下，最终确定了人均社会消费品零售额(x1)、人均固定资产投资(x2)、人均土地面积(x3)、第二产业占GDP比重(x4)、第三产业占GDP比重(x5)、财政支出占GDP比重(x6)、非农从业人员比重(x7)、工业企业利税总额(x8)、人均进出口额(x9)、人均利用外资水平(x10)、外商投资占总投资比重(x11)共11个变量作为经济发展水平综合评价影响因素，相关的变量来源于《江苏省统计年鉴》(2011).

1.2 地理加权主成分分析

地理加权的统计概念由Fotheringham，Brunsdon及Charlton与Lloyd等人给出，地理加权主成分分析通过引入地理加权的一系列算式，将变量间地理位置的交互影响作用纳入计算，从而有效地解决了多元数据中的空间异质性问题.通过不同地点的地理加权均值、地理加权方差及协方差的计算，进而得到地理加权主成分分析的计算结果.

局域协方差矩阵计算公式为：

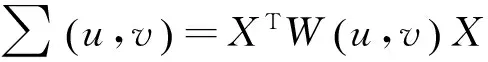
(1)

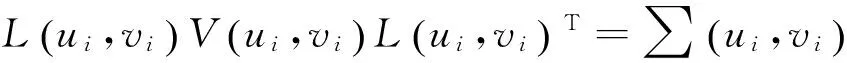
(2)

2 传统主成分分析

首先，采用标准差标准化方法对所选变量进行标准化处理，对标准化数据进行KMO与巴特利球形检验，可知KMO值为0.717，巴特利球形检验在0.01水平下显著，表明所选指标适合进行因子分析.采用方差协方差矩阵的形式进行主成分提取，得到特征值与因子载荷(表1、表2).前3个主成分的特征因子值均大于1，且其累积贡献率接近80%，说明前3个主成分可以解释经济综合发展水平的大部分特征.各主因子载荷矩阵表如表2所示.

表1 主成分分析结果

表2 因子载荷系数

注：最大因子载荷用粗体表示．

由表1知，前3个主成分的累积贡献率为80%左右，可用来反映经济综合发展水平的主要特征.其中，第1个主成分解释了数据结构的53%特性，与非农从业人员比重及人均利用外资水平有较大的正相关性，分别为0.371与0.363，故第1个主成分可以用来表示经济增长驱动力.第2个主成分的解释方差贡献率为14.5%，与第三产业占GDP比重呈较大的相关性，为0.513，而与第二产业所占GDP比重具有较大负相关性，为-0.465，故第2主成分可以用来表征经济产业状况.第三个主成分的方差贡献率仅为10.6%，而与人均土地面积具有最大的负相关性(-0.684)，与其他变量多呈负相关关系，故第3个主成分可代表生产要素构成.

通过对因子得分进行空间可视化(如图1)，可以详细了解地区主因子得分的空间分布状况.由图1.a可知，第1主成分负得分值最高地区多位于苏中与苏北大部分地区，这是由于第一主成分与非农从业人员比重密切相关，苏北、苏中大部分地区经济发展相对滞后，农业从业人员比重较多，而随着经济结构的调整，第一产业所占比重不断下降，农业从业人员多转向第二或第三产业；正得分值较大的地区集聚在苏南的西南地区，多为经济发达地区，具有有利的外商投资政策与环境，对外贸易交流频繁，外资利用规模大.由图1.b可知，第二主成分正的分值多位于苏北西北部地区，而负得分值基本分布于苏中与苏南地区，这与南北地区显著的经济结构差异密切相关.

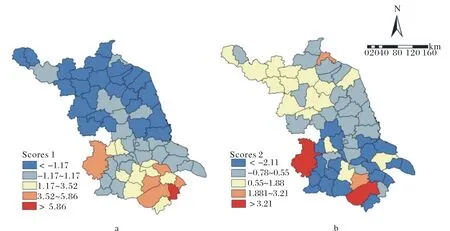
图1 主因子得分图Fig.1 The scores on PC1(a) and PC2(b)

3 地理加权主成分分析

主成分分析通过主要成分的选取，可总体评价识别经济结构的组合特征，而主因子得分呈现出显著的空间分异格局，通过Moran’s I计算进一步判断其局部空间结构，可知第1主成分因子得分的Moran’s I为0.724，在0.01水平下显著，表明第1主成分因子得分在空间分布上具有显著的空间相关性，而第2主成分因子得分的Moran’s I为0.043，且没有通过显著性检验，表明第2因子得分空间分布较随机，这与各主成分载荷变量的地区变化及其空间自相关性有关，而传统主成分分析作为一种非空间统计分析方法，假设地理区位对社会经济现象没有影响作用，故无法识别载荷变量间关系的局部变化.因此，通过地理加权主成分分析进行主成分空间变化的分解，以期找出主导各地区主成分空间格局的主要变量.

3.1 蒙特卡罗检验

在进行地理加权主成分分析，首先采用蒙特卡罗检验方法，检验主成分的特征值是否具有空间变化的非平稳性，原假设认为主成分的特征值在空间上没有变化，备则假设存在着显著的空间变化性.结果如图2所示，由图2知，局部特征值的标准差的p值为0.02，表明在0.05水平拒绝空间平稳性假设，说明主成分的因子载荷、方差贡献率与特征值均存在着显著的局部变化特性.因此，使用地理加权主成分分析技术可以清晰的识别这些特性的空间变化.

图2 地理加权主成分的蒙特卡罗检验Fig.2 Monte Carlo test for the first geographically weighted PC only

3.2 地理加权主成分分析结果

地理加权主成分分析可以得到各研究单元的一系列的特征值、因子载荷与成分得分.根据Fotheringham等人的做法，将地理加权主成分的最大因子载荷进行空间可视化(图3).由图3.a可知，地区的最大因子载荷在空间分布上较集中连续，第1个地理加权主成分的最大因子载荷在空间分布上具有明显的局域特征，其中非农从业人员比重所占地区数量最多，且连续分布于广大苏北地区，这与传统主成分分析的最大载荷变量(0.371)一致，其次人均利用外资水平主导多数地区的地理加权主成分，这与其传统主成分分析的载荷(0.363)有关，其它人均进出口变量位于少数苏南地区，更清晰的说明这些地区的经济活动对外交流联系较为密切，而工业企业利税总额对南京市与镇江市具有最大的影响作用.

图3b为第2个地理加权主成分因子载荷的空间变化，人均土地利用面积、第二产业占GDP比重与第三产业占GDP比重是影响地区主成分的空间变化的主要因素.其中，人均土地利用面积在27个地区具有最大的载荷值，这些区域多呈集中连片分布在广大苏北地区，第二产业占GDP比重在33个地区具有最大的载荷值，这些地区多位于苏南大部分地区，同传统主成分分析的最大负相关变量第二产业占GDP比重(-0.465)较为一致，表明苏南地区的第二产业所占比重较大，第三产业占GDP比重主导着3个地区的经济结构，这与传统主成分分析的最大相关性变量第三产业占GDP比重(0.513)结果存在较大差异.

由图4可知，主成分的方差贡献率呈现出明显的南北分异趋势，这种相似的分异趋势同样体现在其它主成分的局部方差贡献率，其中方差贡献率的高值区多集聚在苏南的东南部分地区，而方差贡献率的低值地区多位于苏北与苏中地区，这与经济变量的冷点区与热点区的南高北低分布相关，方差贡献率的空间格局进一步证实了区域经济变量综合作用的地理分异态势，地区间与变量间均存在明显的位置依赖关系.因此，地理加权主成分分析可以替代传统主成分分析在解释区域综合经济特征的空间变化上.

图3 地理加权主成分的最大因子载荷变量的空间分布Fig.3 Variables with the largest loading on the first and the second geographically weighted PC

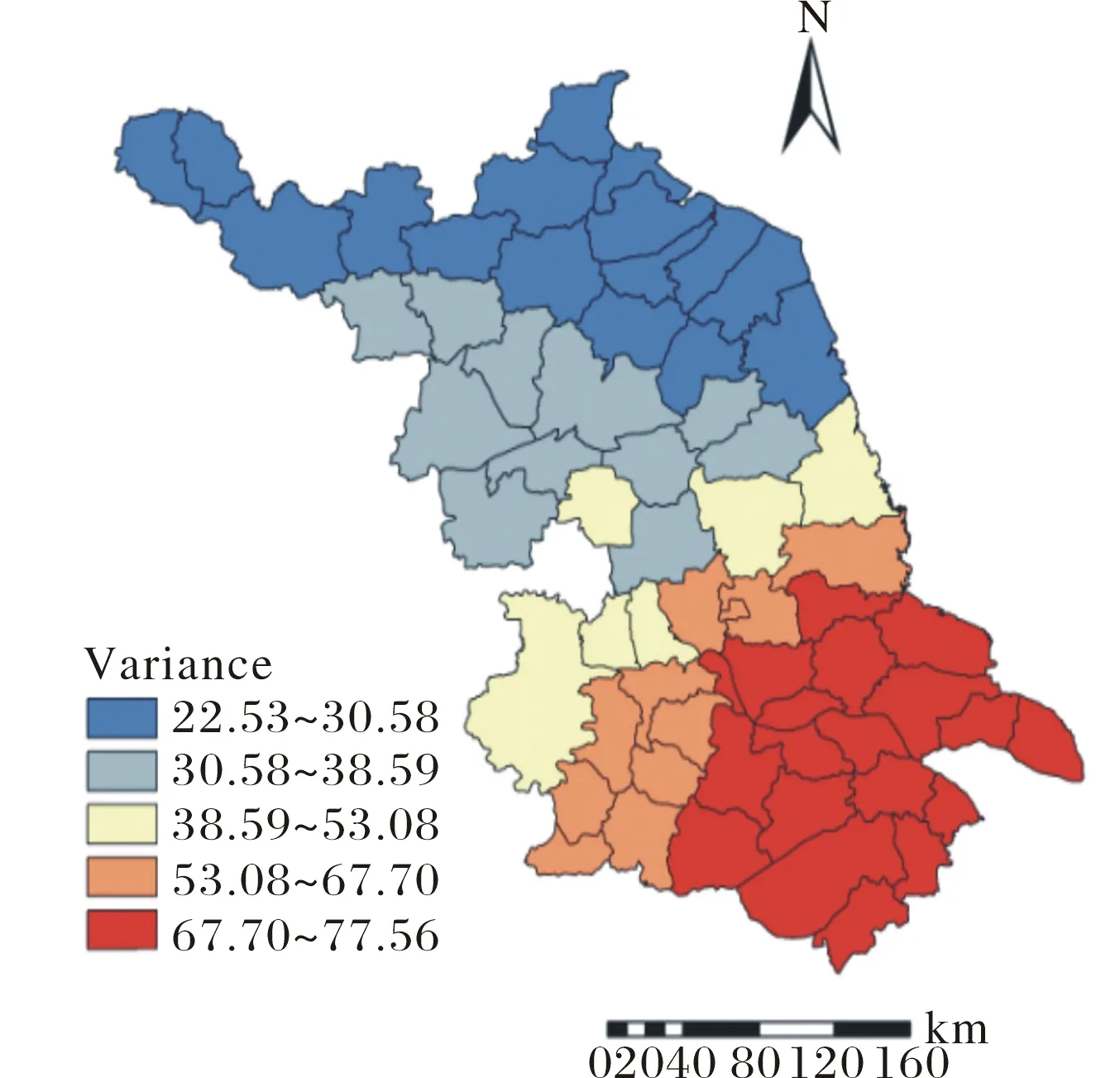
图4 地理加权主成分的方差贡献率Fig.4 Percentage of variance accounted for the first geographically weighted PC

4 结论与讨论

传统主成分分析是一种非空间统计分析方法，它所提取的主要成分并不依赖地理区位，没有考虑到多元数据结构中的空间异质性问题，这导致空间过程和机理往往被忽略.诚然，这种局限性，无益于对社会经济要素空间的分异特征和内在机理的认知.而地理加权主成分分析通过引进地理加权的算式，将传统主成分分析技术扩展到空间主成分层面，有效弥补了传统主成分分析的不足，解释了地区主成分的空间异质性变化趋势，清晰地诊断出导致各主成分空间变化的主要变量.本文结合传统主成分分析与地理加权主成分分析，选取经济发展综合评价的11个变量，探索性的分析了江苏省县域经济综合发展水平的空间变化，得出以下主要结论.

1) 主成分分析有助于辨识多元变量的综合特征，最终选取3个主成分，分别表征经济增长方式、经济结构与经济要素投入.主成分是基于全域的统计，忽略了地区变量空间变化的信息.

2) 空间异质性是普遍存在的，蒙特卡罗检验表明主成分特征值在空间变化上是非平稳的，即影响主成分变化的变量的载荷在空间分布上并不均衡.地理加权主成分的方差贡献率呈现显著的南北分异趋势.因此，地理加权主成分分析可以有效的诊断出地区变化的局部空间效应，地理加权主成分的因子载荷呈现出异质性的空间分布特征.

3) 由第1个地理加权主成分的最大因子载荷图可知，非农从业人员比重所占地区数量最多，这与主成分分析结果较为一致；人均土地利用面积与第二产业占GDP比重主导着大部分地区的第2个地理加权主成分，所有最大载荷变量在空间分布上均呈连续性，这与变量的空间自相关性有关.因此，通过地理加权主成分的因子载荷，可知不同的经济变量对各主成分的载荷影响并不相同，主导地区间各主成分变化的载荷变量存在着明显的空间分异性，地理加权主成分分析可以有效的探索局部地区的变化特性并找出对各主成分空间变化有显著性影响的经济变量.

随着空间数据分析技术的发展与广泛应用，考虑到空间效应的统计分析将是必然的趋势，本文将传统主成分分析扩展到地理加权主成分分析，有效地探索了经济综合特性的空间变化.但本文还存在以下不足：研究单元数量相对较少；且研究指标的选取需要进一步补充；对提取主成分的合理性解释较为主观，今后需进一步完善改进.此外，将这一方法推广到其他社会经济要素综合评价中，对于诊断主导各主成分空间变化的主要变量具有重要意义.

[1] 柯文前， 陆玉麒， 俞肇元， 等. 多变量驱动的江苏省域经济空间格局演化[J].地理学报， 2013， 68(6)：802-812．

[2] JEFFERS J N R. Two case studies in the application of principal component analysis[J].Journal of the Royal Statistical Society Series C(Applied Statistics)， 1967， 16(3):225-236．

[3] WU Q Y， CHENG J Q， CHEN G， et al. Socio-spatial differentiation and residential segregation in the Chinese city based on the 2000 community-level census data: A case study of the inner city of Nanjing[J].Cities， 2014， 39: 109-119．

[4] CHARLTON M， CHRIS B， URSKA D， et al. Principal Component Analysis: from Global to Local[C]. The 13th AGILE International Conference on Geographic Information Science， Guimarães， Portugal， 2010：1-10．

[5] 吴启焰， 吴小慧， CHEN Guo， 等. 基于小尺度五普数据的南京旧城区社会空间分异研究[J].地理科学， 2013， 33(10)：1196-1205．

[6] 潘竟虎， 石培基， 董晓峰. 中国地级以上城市腹地的测度分析[J].地理学报， 2008， 63(6)：635-645．

[7] 孙姗姗， 朱传耿， 李志江. 淮海经济区经济发展差异研究[J].地理学报， 2009， 64(8)：924-934．

[8] 刘传明， 曾菊新. 县域综合交通可达性测度及其与经济发展水平的关系——对湖北省79各县域的定量分析[J].地理研究， 2011， 30(12)：2209-2220．

[9] OPENSHAW S， CHARLTON M， WYMER C， et al. A mark 1 geographical analysis machine for the automated analysis of point data sets[J].International Journal of Geographical Information Systems， 1987， 1(4): 335-358．

[10] LLOYD C D. Analysing population characteristics using geographically weighted principal components analysis: a case study of Northern Ireland in 2001[J].Computers， Environment and Urban Systems， 2010， 34(5):389-399.

[11] BINBIN L， PAUL H， ISABELLA G， et al. GWmodel: an R package for exploring spatial heterogeneity.GISRUK2013，Liverpool，UK，2013．

[12] BINBIN L， PAUL H， MARTIN C， et al. The GWmodel R package: Further Topics for Exploring Spatial Heterogeneity using Geographically Weighted Models[EB/OL]. arXiv:1312.2753, 2013, 1:18.

[14] GOODCHILID M F. The Validity and Usefulness of Laws in Geographic Information Science and Geography[J].Annals of the Association of American Geographers， 2004， 94(2):300-303．

[15] 程叶青， 王哲野， 张守志， 等. 中国能源消费碳排放强度及影响因素的空间计量[J].地理学报， 2013， 68(10)：1418-1431．

[16] 洪国志， 胡华颖， 李 郇. 中国区域经济发展收敛的空间计量分析[J].地理学报， 2010， 65(12)：1548-1558．

[17] 梅志雄， 徐颂军， 欧阳军. 珠三角县域城市潜力的时空关联结构演变[J].地理学报， 2014， 69(4)：497-509．

[18] ANSELIN L. Thirty years of spatial econometrics[J]. Papers in Regional Science， 2010， 89(1): 3-25．

[19] FOTHERINGHAM A S， BRUNSDON C. Local forms of spatial analysis[J].Geographical Analysis， 1999， 31:340-358．

[20] FOTHERINGHAM A S， BRUNSDON C. Geographically weighted Regression: the analysis of spatially varying relationships[M].Chiceste:Wiley， 2002，196-202．

[21] PAUL H， CHRIS B， MARTIN C. Geographically weighted principal components analysis[J].International Journal of Geographical Information Science， 2011， 25(10):1717-1736．

[22] GOLLINI I， LU B ， CHARLTON M， et al. GWmodel: an R Package for Exploring Spatial Heterogeneity using Geographically Weighted Models[EB/OL]. arXiv:1306.0413，2013，1:19．

[23] SANDEEP K， RATTAN L， LLOYD C.D. Assessing spatial variability in soil characteristics with geographically weighted principal component analysis[J].Comput Geosci， 2012， 16(3):827-835．

[24] 桑 秋， 张平宇， 高晓娜， 等. 辽中城市群县域综合发展水平差异的时空特征分析[J].地理科学， 2008， 28(2)：150-155．

[25] 仇方道， 朱传耿， 单勇兵， 等. 中国县域综合实力评价与区域分异特征[J].地理科学， 2004， 24(4)：392-398．

[26] 赵玉芝， 董 平. 江西省县域经济差异特征及其成因分析[J].人文地理， 2012， 27(1)：87-91．Geographically weighted Principal Components Analysis of regional development——a case study of Jiangsu Province

MA Zhifei， LI Zaijun， ZHANG Yaqian， WU Qiyan

(School of Geography Science， Nanjing Normal University， Nanjing 210023)

Geographically weighted Principal Component Analysis identifies the spatial variation of variance contribution in each principal component and the main factors dominating them. In the present study， based on the comprehensive evaluation of economic development， the principle components were extracted from economic characteristics of sixty-six counties or cities in Jiangsu Province in combination of the traditional and geographically weighted Principal Component Analysis. Results reveal that three principal components are extracted， representing the growth pattern， structure and stimuli of economy， respectively. The Monte Carlo test shows it unreasonable to ignore the spatial effects of eigenvalues and components loadings. Geographically weighted components loadings dominant the characteristics of economic structures in different region， which appears to be concentrate and confluent. Besides the variance contribution of the indicated components significantly displays the north-south differentiation pattern. These suggest that the geographically weighted principal component analysis is conductive to further understanding the spatial characters and internal mechanism of economic components.

comprehensive evaluation of economic development； Principal Component Analysis； geographically weighted Principal Component Analysis； Jiangsu Province

2015-09-22.

国家自然科学基金项目(41271176)；教育部人文社科基金项目(12YJAZH159)；国家社会科学基金项目(12BSH027)．

1000-1190(2016)02-0276-06

F207

A

*通讯联系人. E-mail: chiyanwu@126.com.