分数阶Van der pol振子网络的混沌同步
2016-11-29毛北行王东晓
毛北行, 王东晓
(郑州航空工业管理学院 理学院, 郑州 450015)
分数阶Van der pol振子网络的混沌同步
毛北行*, 王东晓
(郑州航空工业管理学院 理学院, 郑州 450015)
研究了一类分数阶Van der pol复杂振子网络的混沌同步问题,基于Lyapunov稳定性理论和分数阶微积分的相关理论,给出了两种实现同步的控制方案,仿真结果表明了方法的可行性.
分数阶系统; 振子网络系统; 混沌同步
分数阶微积分理论已有300多年的历史,近年来分数阶系统逐步成为研究的热点.另一方面,混沌同步及其应用已成为研究的热点并取得了丰富的成果[1-7],文献[8]研究了一类分数阶非线性系统的混沌同步控制问题.文献[9]研究了基于投影法的不确定分数阶混沌系统自适应同步,讨论了一类具有未知参数,未知非线性函数及外部扰动的分数阶系统,文献[10]研究了一类不确定分数阶混沌系统的同步控制,结合状态观测器和自适应方法,提出了一种符合工程实际的控制方案,文献[11]基于反馈控制研究了一类分数阶时滞神经网络系统的混沌同步问题,文献[12]研究了一类Van der pol振子组成的动态复杂网络的混沌同步问题,但研究的不是分数阶系统,本文在上述研究的基础上研究了一类分数阶Van der pol复杂振子网络的混沌同步问题,给出了两种实现同步的控制方案,仿真算例表明了方法的有效性.
1 预备知识:
定义1[13]Caputo分数阶导数定义为:
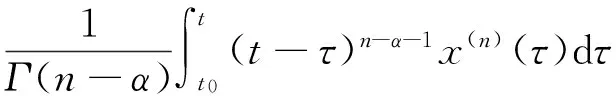
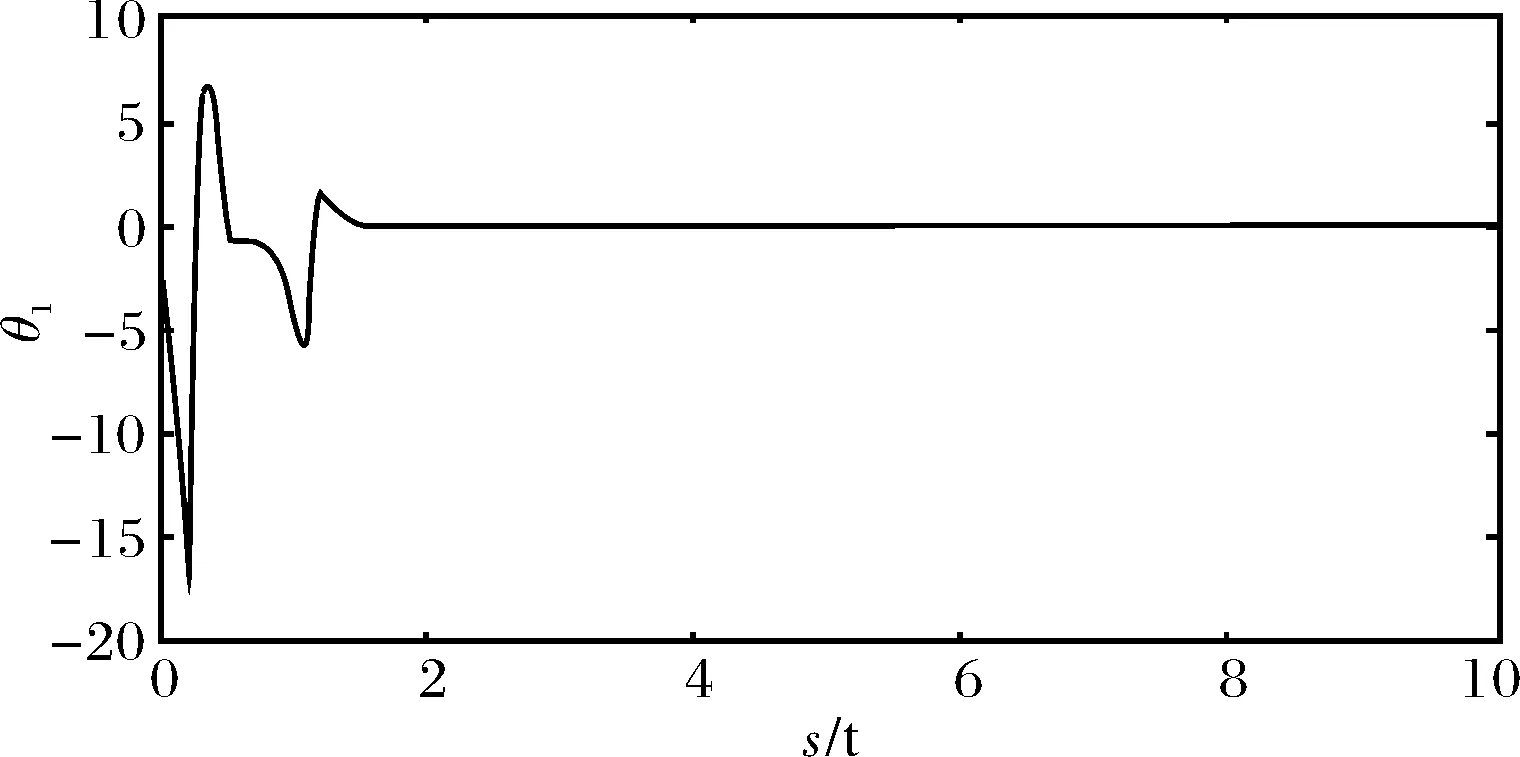
n-1<α 定义2[14]单参数Mittag-Leffler函数: 定义3[14]双参数Mittag-Leffler函数: 有 Eα(z)=Eα,1(z),E1,1(z)=ez. 引理1[14]若α<2,β∈∀R,πα/2<ρ 引理2[15]若V(t)是[0,∞)上的连续函数,满足DαV(t)≤-ηV(t),则有:V(t)≤V(t0)Eα(-η(t-t0)α),其中α∈(0,1),η>0为常数. Van der pol系统为: (1) 考虑上述N个具有相同结构的Van der pol振子耦合而成的分数阶动态复杂网络: 以上述系统(2)作为主系统,则其从系统为: (3) 定义系统误差为:ei(t)=yi(t)-xi(t),则有 bq2[(cTyi)3-(cTxi)3]+ui(t). (4) 2.1 同步方案一 根据引理2很容易得到 V(t)≤V(t0)Eα(-η(t-t0)α), 2.2 同步方案二 (5) (6) 考虑具有线性耦合的Van der pol动态电路模型[16]: 其中,i1,i2分别为通过电感L1,L2的电流,V1,V2分别为电容C1,C2两端的电压,R是电阻,NR是一个非线性电阻,其电压电流特性为: 上述分数阶系统可以描述为: i=1,2,3,4, L1=0.12 H,L2=0.1 H,R=0.001 Ω, R0=2.5 Ω ,q1=-0.01,q2=0.01, 系统初始值设置为:V11=0,V12=0,i11=0,i12=0,V21=0.25,V22=0.5,i21=i22=0.25,V31=-0.5,V32=i31=i32=-0.25,V41=0,V42=0.1,i41=0.5,i42=0, 定义系统误差为:ei(t)=yi(t)-xi(t),则其误差系统为: bq2[(cTyi)3-(cTxi)3]+ui(t). α=0.93,计算得定理1中k=122,η=2,系统误差曲线如图1~图4所示;定理2中k=122,ε=2,系统误差曲线如图5~图8所示. 图1 定理1中第1误差变量e1Fig.1 The first error varible e1 of Theorem 1 图2 定理1中第2误差变量e2Fig.2 The second error varible e2 of Theorem 1 图3 定理1中第3误差变量e3Fig.3 The third error varible e3 of Theorem 1 图4 定理1中第4误差变量e4Fig.4 The fourth error varible e4 of Theorem 1 图5 定理2中第1误差变量e1Fig.5 The first error varible e1 of Theorem 2 图6 定理2中第2误差变量e2Fig.6 The second error varible e2 of Theorem 2 图7 定理2中第3误差变量e3Fig.7 The third error varible e3 of Theorem 2 图8 定理2中第4误差变量e4Fig.8 The fourth error varible e4 of Theorem 2 其中图i(i=1,2,…,8)中横坐标为时间t,单位为s,纵坐标为ei(t),单位为m. 研究了一类分数阶多个Van der pol振子组成的复杂网络的混沌同步问题,基于稳定性理论给出了实现同步的两种方法,并给出了控制器的设计,研究表明满足一定的条件下,主从系统是混沌同步的,数值仿真表明了方法的正确性. [1] 方 洁, 陆 程. 非线性干扰观测器方法实现受扰混沌系统同步[J].河南科技大学学报自然版, 2012, 33(6):35-39. [2] 吕 翎, 李 纲, 张 檬, 等. 全局耦合网络的参数辨识与时空混沌同步[J].物理学报, 2011, 60(9):5051-5056. [3] 李德奎, 褚衍东, 张建刚. 带有时变时滞和线性耦合的复杂网络同步[J].昆明理工大学学报, 2013, 36(2):50-55. [4] 褚衍东, 李红敏, 张建刚, 等. 带有时变时滞和非线性耦合的复杂网络同步[J].安徽大学学报(自然科学版), 2012, 36(2):9-14. [5] YU L, LI G,GUO Y . Generalized chaos synchronization of a weighted complex network with different nodes[J].Cjin Phys B, 2010, 19(8):5071-5077. [6] 毛北行, 李巧利. 具有非线性耦合的Lurie动态网络的函数投影同步[J].华中师范大学学报(自然科学版), 2015, 49(1):47-52. [7] MEI J, JIANG M, WANG J. Finite-time structure identification and synchronization of drive-response systems with uncertain parameter[J].Commun Nonlinear Sci Numer Simulat, 2013, (18):999-1015. [8] 邵书仪, 陈 某. 一类分数阶非线性混沌系统的同步控制[J].计算机仿真, 2015, 32(4):394-398. [9] 张友安, 余名哲, 耿宝亮. 基于投影法的不确定分数阶混沌系统自适应同步[J].电子与信息学报, 2014, 37(2):454-460. [10] 严胜利, 张昭晗. 一类不确定分数阶混沌系统的同步控制[J].系统仿真技术, 2013, 9(4):366-370. [11] 张云雷, 吴超然. 基于反馈控制的分数阶时滞神经网络的同步[J].重庆工商大学学报(自然科学版), 2014, 31(12):49-53. [12] 李鑫滨, 王腊梅, 刘 仙. 基于动态复杂网络的Van der pol振子同步[C]//Proceeding of the 29th Chinese Control Conference ,2010,Beijing, China: 781-785. [13] Podlubny A. Fractional Differential Equation[M].San Diego: Academic Press,1999. [14] Hilfer R. Applications of Fractional Calculus in Physics[M].Singapore: World Scientific, 2000. [15] Srivastava H,OWA S. Univalent Functions, Fractional Ccalculus and Their Applications[M].New Jersey:Prentice Hall, 1989. [16] MIN X, CAO J. Synchronization in general complex dynamical networks with coupling delays[J].Physica A:Statistical Mechanics and its Applications,2004,343(15):263-278. Chaos synchronization of fractional order Van der pol oscillators network systems MAO Beixing, WANG Dongxiao (College of Science, Zhengzhou Institute of Aeronautical Industry Management, Zhengzhou 450015) In the present work, the chaos synchronization problem is studied on fractional order Van der pol oscillators complex network systems. A controller is proposed based on Lyapunov stability theory and fractional order systems theory. Two control project are presented and sufficient conditions are obtained for errors systems asymptotically stable. Numerical simulations example of chaotic system verify the effectiveness of the proposed method. fractional order systems; oscillators network systems; chaos synchronization 2015-08-22. 国家自然科学基金项目(11404291);河南省高等学校青年骨干教师资助计划项目(2013GGJS-142);河南省科技厅基础与前沿研究计划项目(142300410410);河南省高等学校重点科研项目(15B110011). 1000-1190(2016)02-0202-04 O193 A *E-mail: bxmao329@163.com.


2 主要结果
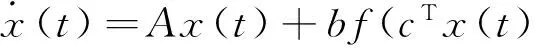

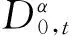
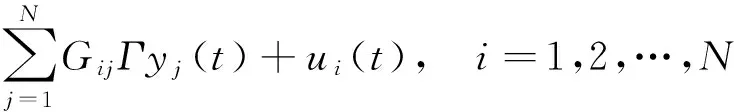

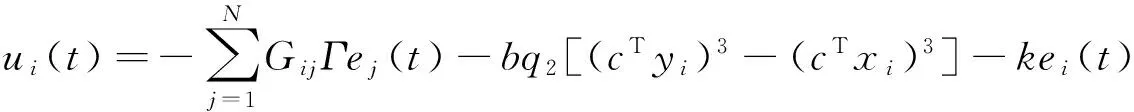
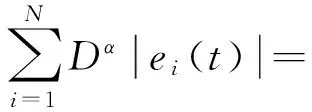

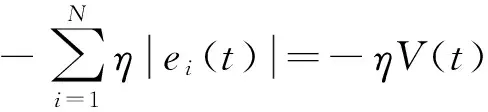
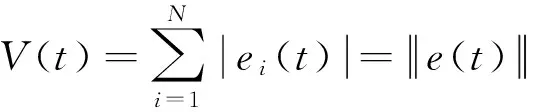




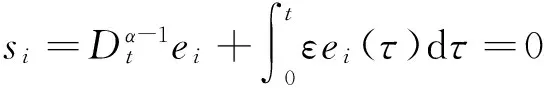
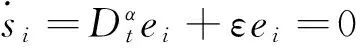
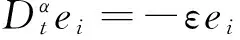
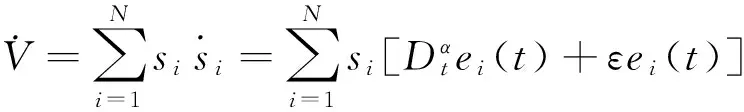
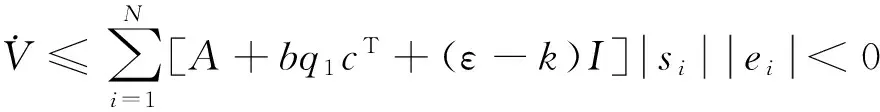
3 数值算例
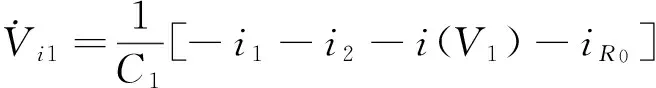
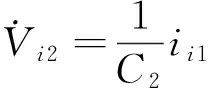
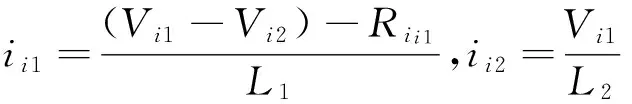
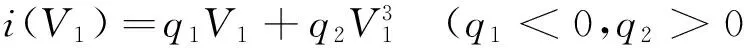
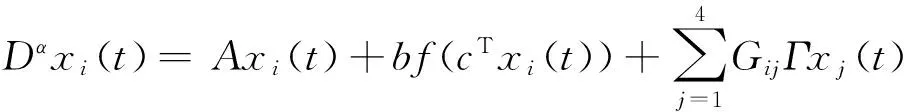

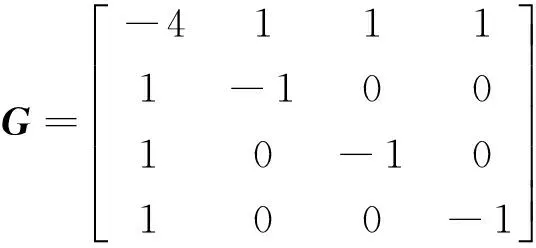






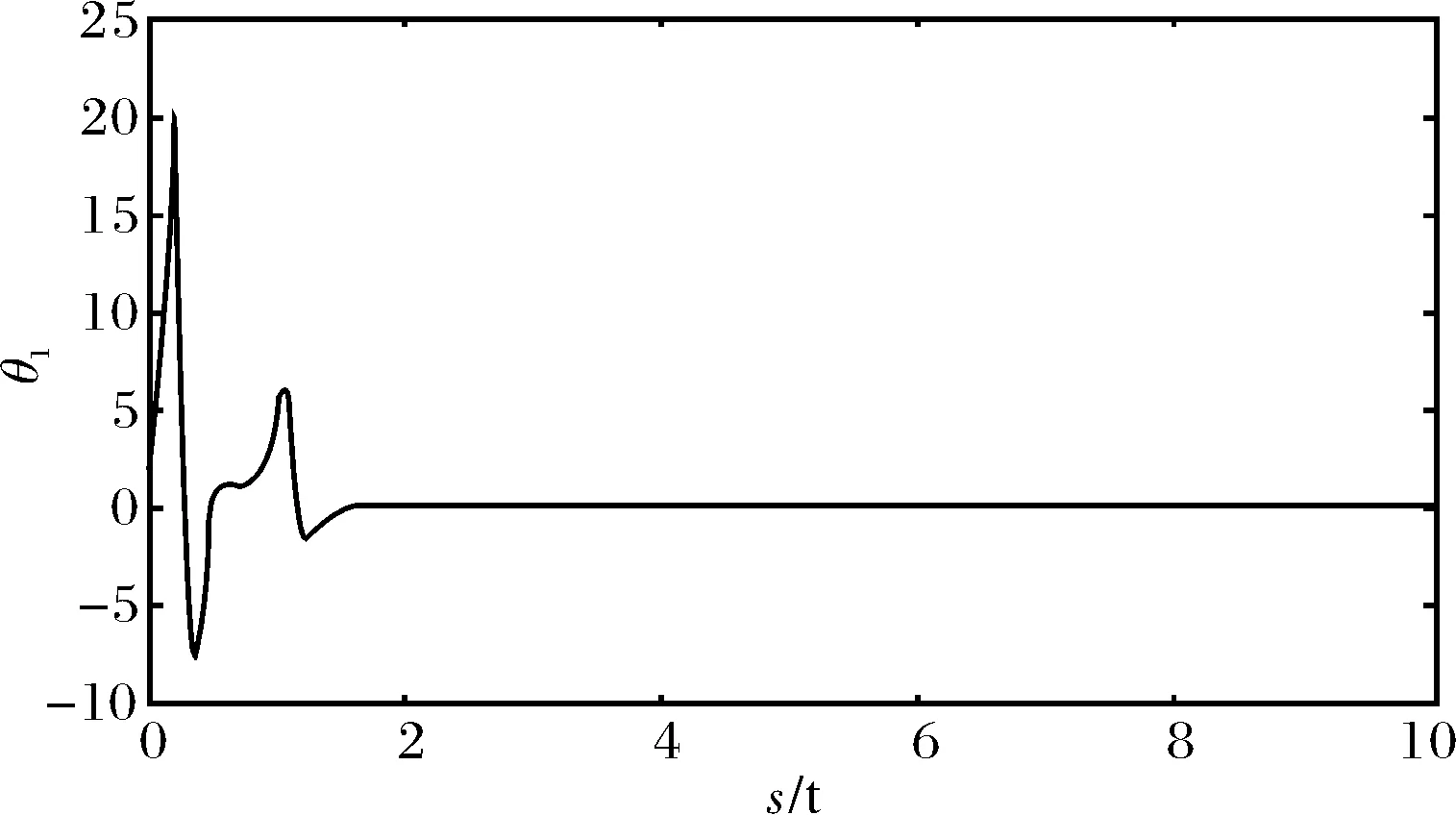

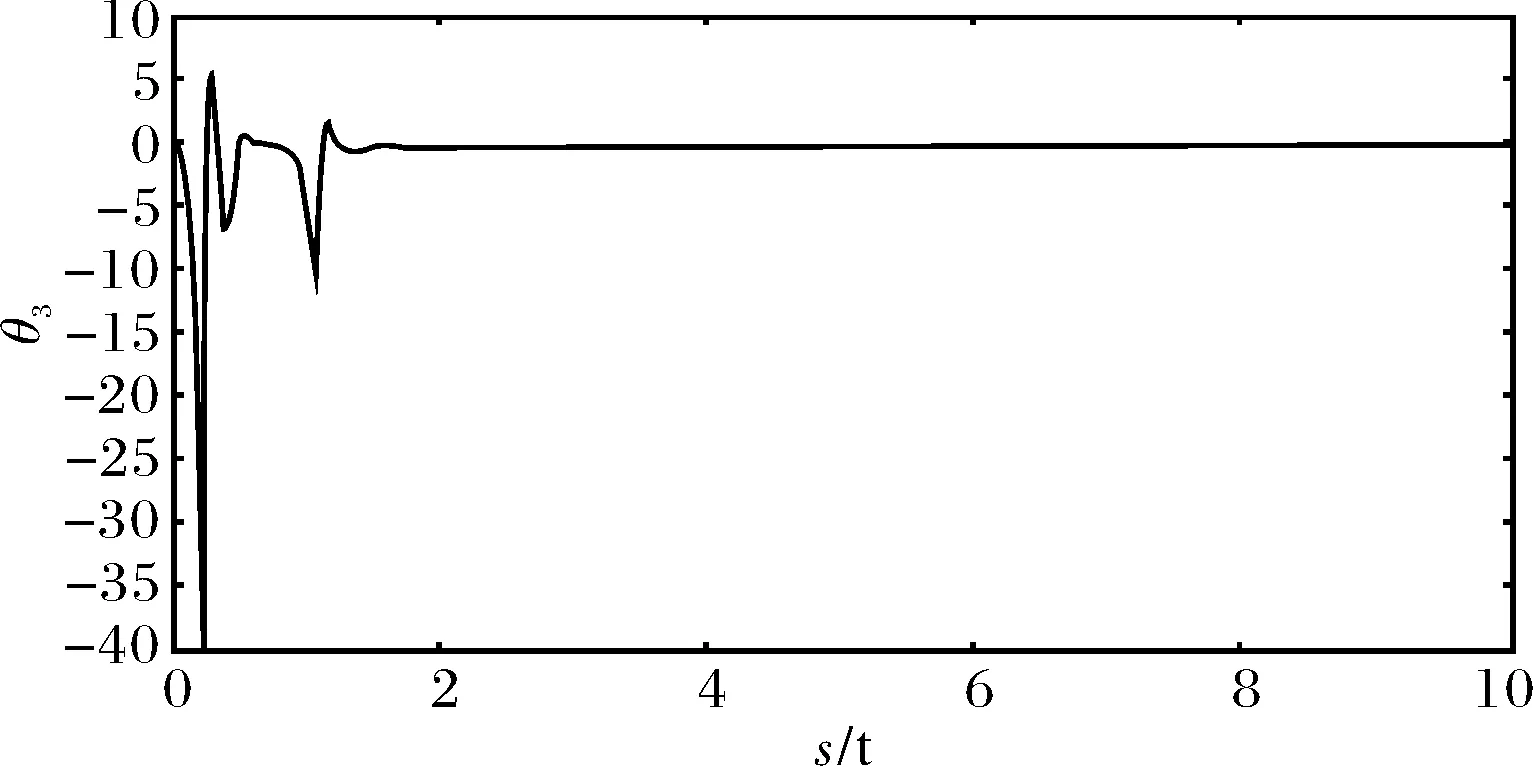
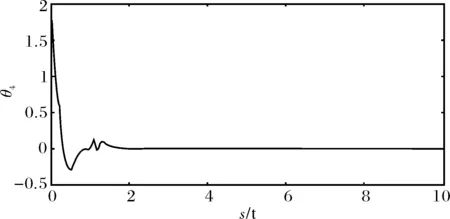
4 结束语
