基于随机跳违约强度的可转换债券的定价

潘 坚, 肖庆宪

(1.上海理工大学 管理学院, 上海 200093;2.赣南师范学院 数学与计算机科学学院, 江西 赣州 341000)



基于随机跳违约强度的可转换债券的定价

潘 坚1,2*, 肖庆宪1

(1.上海理工大学 管理学院, 上海 200093;2.赣南师范学院 数学与计算机科学学院, 江西 赣州 341000)

在约化模型框架下,研究具有随机跳违约强度的可转换债券定价问题.应用风险中性定价原理建立随机跳跃幅度服从双指数跳扩散过程,股票价格服从时变扩散模型,随机利率服从Hull-White模型且两两相关的定价模型.利用鞅方法得到了此定价模型的解析解,拓展了相关文献的结论.

跳违约强度; Hull-White利率模型; 约化模型; 鞅方法; 可转换债券定价

作为重要的金融工具之一,可转换债券是一种具有期权特性的公司债券,它赋予投资者可选择将债券持有至到期日,获得本金和利息,也可以在约定的时间将债券转换成公司股票的权利.鉴于此,可转换债券在金融市场受到投资者的追捧.但是,和所有投资工具一样,可转换债券也会使投资者遭到损失.如果发行公司倒闭,那么债券的持有人就会损失投资于债券的资金,可转换债券尤其可能发生这种情况,这是因为可转换债券的地位通常低于公司的其它债券.此外,可转换债券的期限较长,利率的影响变得较为突出,因此,除了违约支付的风险外,可转换债券还存在利率风险.基于违约风险和利率风险的可转换债券的定价,是近几年国内外学者关注的热点.

目前,具有违约风险和利率风险的可转债定价模型有两类:一类是基于期权定价理论的结构化模型[1],另一类是基于强度理论的约化模型[1].基于结构化模型研究可转换债券的定价始于Ingersoll[2],他把Black-Scholes的期权定价思想引入到可转换债券定价中,考虑了以公司价值为基础变量的单因素结构化模型; Brennan和Schwartz[3]对Ingersoll的单因素结构化模型进行了扩展,把利率的不确定性引入模型当中,建立了以利率和公司价值为基础变量的双因素模型.目前,以公司价值为基础变量研究可转换债券定价都是以这两个模型为基础.与结构化模型不一样的是,在约化模型中,违约被看成是一个完全不可预测的事件,违约过程用Poisson过程来描述,即第一次发生跳时公司违约.近年来,有不少学者基于约化模型研究可转换债券的定价.Takahashi等[4]在违约强度是股价反比例函数情形下研究了可转换债券的定价;Ayache等[5]在常数违约强度下,把可转换债券的价值作为一个整体研究对象,研究了带违约风险的可转换债券定价模型,此定价模型是一个耦合的偏微分方程组,没有解析解,用有限差分法考虑了数值解;Bielecki等[6]运用鞅测度方法研究了常数违约强度下博弈期权的定价和套期保值,并将其应用到可转换债券的定价和对冲中;Bielecki等[7]在文献[6]的基础上进一步研究了由标的资产股票、可转换债券和有关信用违约互换组成的基本金融市场框架下可转换债券的定价,在此框架下将可转换债券的价格转化为相应变分不等式的粘性解并给出了近似计算的收敛性证明.国内,Huang Jianbo,liu Jian和Rao Yulei[8]利用二叉树方法考虑了常数违约强度下具有利率风险和信用风险的可转换债券的定价;王伟和赵奇杰[9]考虑了常利率情形下带有违约风险的可转换债券的定价,假定市场中可转换债券的随机违约强度服从Vasicek模型,利用鞅方法得到了该模型的解析定价公式.

在上述模型中,为了简化计算,违约强度假定为常数或连续的扩散随机过程.实际上,发行公司在可转换债券续存期间可能会受到国家宏观经济调控等外部政策的影响,使公司利润大幅降低,财务风险加大,导致公司出现危机或破产.在约化模型中,这些不可预见的事件可能会导致违约强度发生剧烈的变化,苏小囡和王文胜[10]在随机跳违约强度下研究了欧式期权的定价,随机跳的幅度假定服从正态分布.本文的主要工作和创新点是:基于约化模型研究具有随机跳违约强度的可转换债券定价问题,假设违约强度服从更符合实际的双指数跳扩散过程[11],并假定市场中无风险利率服从一个与标的股票相关的Hull-White模型.利用鞅方法得到可转换债券的解析定价公式,推广了相关文献的结果.最后,借助Matlab软件讨论了跳违约强度对可转换债券价值的影响.结果表明:双指数跳扩散过程下可转换债券的价值走势是下凸的,这表明跳违约强度会影响可转换债券的价值,可转换债券在债券存续期间存在一个临界点,在临界点处公司可能发生违约.

1 模型的建立

下面给出建立模型所需的一些基本假设.

1.1 基本假设

1) 考虑一个随机的金融市场,不确定性由完备的概率空间(Ω,F,Q,(Ft)0≤t≤T)来表示,Q为风险中性鞅测度,{Ft}t≥0为公司信息流,满足自然假设,即右连续、单调递增.

2) 股票的价格St服从如下时变扩散模型:

dSt=St[(rt-qt)dt+σ1(t)dW1(t)],

(1)

其中,qt为红利率,σ1(t)为股票的波动率,W1(t)为标准的布朗运动.

3) 随机利率rt采用可以根据初始期限结构进行校准的Hull-White模型:

drt=a2[b2(t)-rt]dt+σ2dW2(t),

(2)

其中,a2为利率回归长期均值的速度,b2(t)为利率的长期均值,σ2为利率的波动率,W2(t)为标准的布朗运动.

4) 定义违约强度λt是具有跳违约强度的随机微分方程[10-11]:

dλt=a3[b3(t)-λt]dt+σ3dW3(t)+

(ey-1)dNt,

(3)

其中,a3为违约强度回归长期均值的速度,b3(t)为违约强度的长期均值,σ3为违约强度的波动率,W3(t)为标准的布朗运动,Nt是跳强度为η的泊松过程且跳跃幅度为y.本论文假定y服从双指数分布,即y的密度函数为:

f(y)=pη1e-η1y1{y≥0}+(1-p)η2eη2y1{y<0},

η1>1,η2>0,

其中,p表示强度向上跳的概率,1-p表示强度向下跳的概率,1{·}是一个示性函数.

5) cov[dWi(t),dWj(t)]=ρij(dt), |ρij|<1,i,j=1,2,3,且i≠j,常数ρij表示两个随机源的相关系数.此外,Nt,y与W1(t),W2(t),W3(t)相互独立.

6) 在实际的可转换债券市场中,可转换债券的种类繁多.根据林海和郑振龙的研究结果[12],可转换债券在国内债券市场上一般不会被提前执行.因此,假定可转换债券的转换只发生在到期日T,即在T时刻债券持有者有权利选择是持有股票还是持有债券.如果在到期日,用债券转换股票后的价值超过债券的价值,那么债券持有者可选择转换.相反,如果在到期日,用债券转换股票后的价值不超过债券的价值,债券持有者则不选择转换.令φ(T)表示可转换债券在到期日的收益,则有

(4)

其中,Pb=MeiT表示以票面利率i计算的单纯的债券价值(债券利息按连续复利计算),M表示可转换债券的面值,C表示约定的转换价格.

7) 市场不存在套利机会、无交易费和税收,但债券存在违约风险,即当可转换债券的发行方发生违约时,在T时刻可转换债券的持有者仅收到先前承诺支付的一部分,即hφ(T),0≤h≤1,其中,h是回收率且为常数;如果可转换债券的发行方不发生违约,则债券的持有者在T时刻接受先前承诺的支付φ(T).

1.2 建立模型

为建立随机利率模型下具有跳违约风险的可转换债券的定价模型,引入带滤流的概率空间(Ω,G,(Gt)0≤t≤T,Q),总的域流是Gt=Ft∨Ht,其中,Ft=σ(Su,0≤u≤t)∨σ(ru,0≤u≤t)∨σ(λu,0≤u≤t)反映市场上除了公司违约信息之外的信息,而Ht=σ(I{τ≤u},0≤u≤t)反映公司的违约信息.由Jarrow和Yu有关条件概率的知识[13],可以得到:

(5)

其中,GT=FT∨Ht.因此在模型假设下,由风险中性定价理论,具有跳违约风险的可转换债券在t时刻的值V(S,r,λ,t)可表示为:

V(S,r,λ,t)=

(6)

下面利用条件数学期望的平滑性[14-15]以及Bielecki和Rutkowski的结论[1]消去(6)中的违约时间τ,于是有

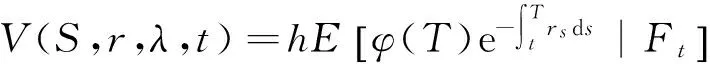
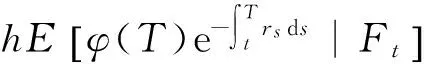
I1+I2.

(7)

其中,

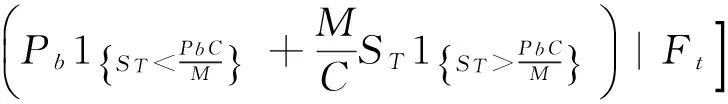
因此求解V(S,r,λ,t),只需计算I1和I2即可.

2 模型的求解

下面利用鞅方法的测度变换计算I1和I2.

其中,

m(t,T,a2)=1-e-a2(T-t),

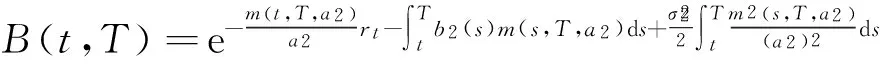
证明由于利率是随机的,引入远期鞅测度QT,即定义关于QT的Radon-Nikodym导数:

由Ito公式和方程(2),有

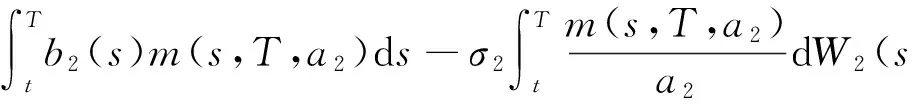
(8)

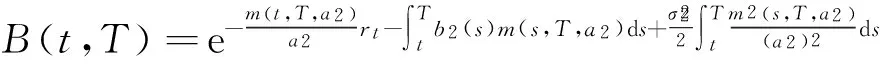
(9)

从而由(8)和(9),可以得到

根据Girsanov定理,

根据Bayes法则,I1在鞅测度QT下为:

I11+I12.

(10)

(11)

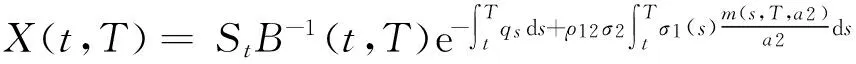
(12)

此外由标准正态分布的性质，在概率测度QT下,logST满足正态分布,其均值和方差分别为:

E[logST]=logSt-logB(t,T)-

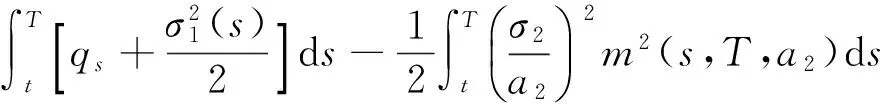
因此,由(11)可以得到

I11=hPbB(t,T)N(d1),

(13)

其中,

为了计算

引进新的Radon-Nikodym导数:

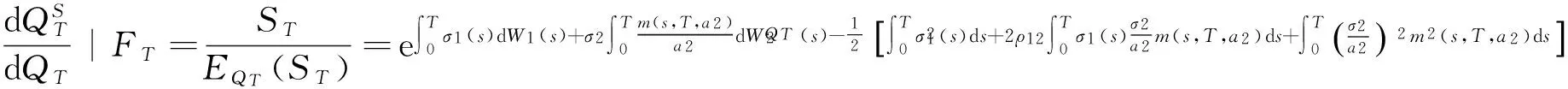
根据Girsanov定理,可以得到

(14)

(15)

E[logST]=logSt-logB(t,T)+

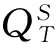
(16)

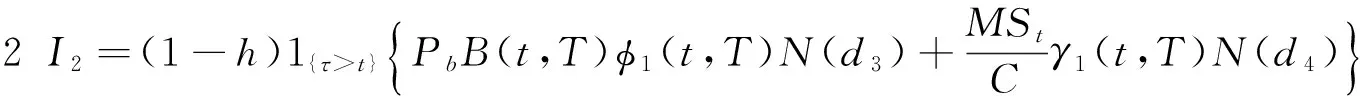
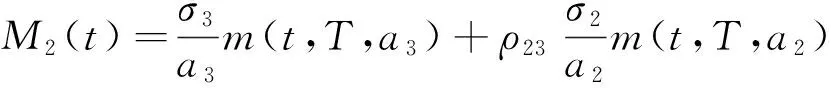
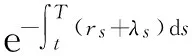
(17)

由Ito公式,(3)和(8),可以得到

(18)

(19)

由(18)和(19)可以得到

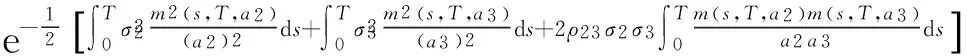
根据Girsanov定理,可以得到

(20)

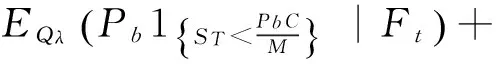
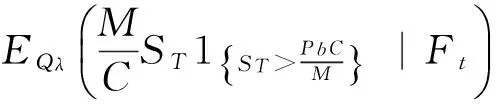
(1-h)1{τ>t}φ(t,T)(I21+I22).

(21)

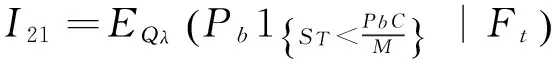
(22)

记γ(t,T)=EQλ(ST),对(22)取数学期望,可以得到

(23)

此外,由标准正态分布的性质:在概率测度Qλ下,logST满足正态分布,其均值和方差分别为:

E[logST]=logSt-logB(t,T)-

因此,由方程(22)可以得到

(24)

其中,

根据Girsanov定理,可以得到

(25)

(26)

由标准正态分布的性质:在概率测度QS下,logST满足正态分布,其均值和方差分别为:

E[logST]=logSt-logB(t,T)+

于是根据Bayes法则和(26),I22在鞅测度QS下为:

(27)

由引理1和引理2,可以得到如下定理1,

定理1Hull-White利率模型下具有随机跳违约风险的可转换债券在t时刻的值为:

(28) 其中,h是回收率,其它变量和参数见引理1和引理2.

由定理1,可以得到常利率下具有违约风险的可转换债券在t时刻的值,只需在定理中令a2=0,b2=0,σ2=0,ρ12=ρ23=0,于是有

推论1常利率下具有跳违约风险的可转换债券在t时刻的值为:

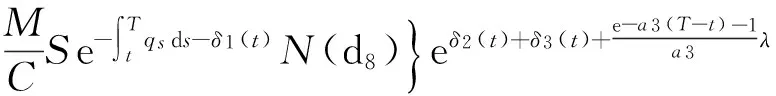
其中,

d5=

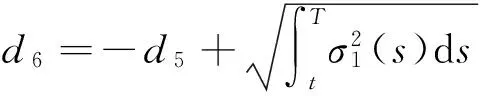
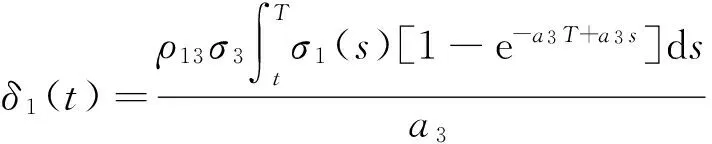
δ2(t)=

其它有关参数见引理1和引理2.

在推论1中如果令η=0,可以得到常利率下不具有跳违约风险的可转换债券在t时刻的值,即

推论2常利率下不具有跳违约风险的可转换债券在t时刻的值为:

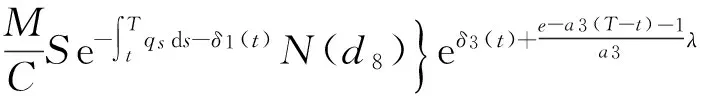
推论2中的参数见推论1.

注11)定理和推论1涉及到违约强度的参数估计问题,可从市场上的债券报价和股票价格中推得; 2)推论2与文献[9]中的结果完全一致; 3)定理、推论1和推论2表明:具有违约风险的可转换债券的价值可以独立地分解成两部分——无违约部分加违约部分.

3 数值算例

为了评价模型的性能,下面将利用数值化的方法来凸显跳违约强度(双指数跳扩散过程)和随机利率对可转换债券价值的影响.基本参数如下表1.

表1 基本参数

3.1 双指数跳扩散对具有违约风险可转换债券价值的影响

下面利用Matlab软件编程分别计算了不同跳强度,不同跳跃幅度(包括向上和向下)和不同跳跃概率下的可转换债券的价值,如表2～表4所示.

表2 不同跳强度η下的可转换债券的价值

下的可转换债券的价值

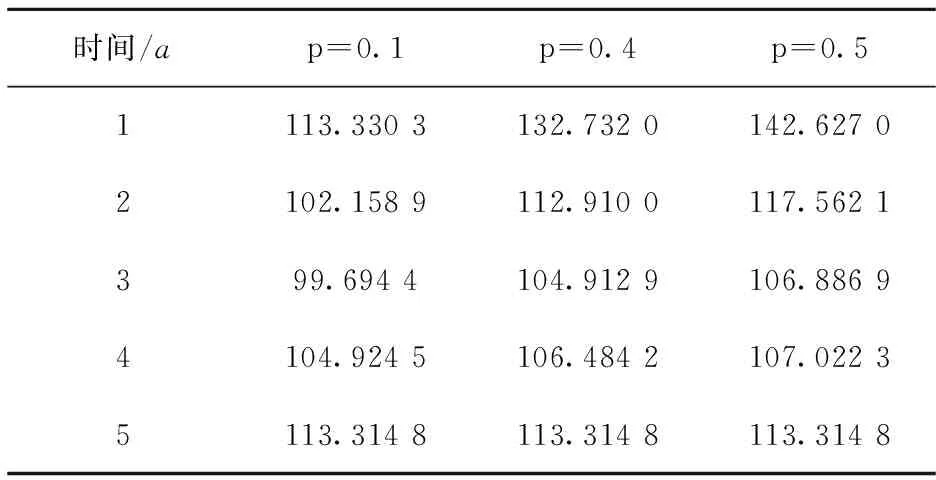
表4 不同跳跃概率p下的可转换债券的价值

从表2～表4可以看出: 1)双指数跳扩散过程下可转换债券的期限结构都是先减后增,这表明在可转换债券的续存期限内存在拐点,可转换债券在对应的拐点上可能违约; 2)跳强度η=0表示违约过程是连续过程,即违约风险没有跳风险,此时的定价公式(28)是Hull-White利率模型下不具有跳违约风险的可转换债券的定价公式.随着跳强度η的增大,基本参数下同期可转换债券的价值变的更高,其金融意义是跳强度的增大意味着可转换债券极有可能发生违约; 3)同期可转换债券的价值随着向上(或下)跳跃幅度(跳跃概率)的增大而增加(或减少),其金融意义也是显然的,即向上跳跃幅度(跳跃概率)的增大,表明可转换债券发行方发生违约的可能性在增加,是对投资者愿意承担风险的一种补偿,反之则相反.

3.2 利率和跳违约双重风险对可转换债券价值的影响

下面同时考虑随机利率和跳风险对可转换债券价值的影响,利用Matlab软件,得到了3种情形下可转换债券的期限结构关系图.

图1 3种情形下的可转换债券的期限结构Fig.1 The term structure of convertible bond in three different cases

从图1可以看到: 1)双指数跳扩散过程下可转换债券的价值走势是下凸的,这意味着随着时间的推移,可转换债券存在拐点,在拐点处可能发生违约; 2)常利率情形下不具有跳违约风险的可转换债券价值的期限结构随时间的临近到期而增大,这是因为随着可转换债券的到期,由于票面利率的原因,持有债券的投资者能得到更多的利息.此外,由于可转换债券兼具了期权的性质,可转换债券所隐含的期权的价值也在逐渐增加; 3)具有随机跳违约风险和利率风险下可转换债券的价值高于常数利率且不具有跳风险情形下可转换债券的价值,主要是跳风险提升了可转换债券的价值,也是对投资者承担跳风险和利率风险的一种补偿.

4 结束语

利率风险和违约风险是可转换债券定价中不可忽视的风险,但在现有的可转换债券定价模型中很少一起涉及,特别是涉及跳违约风险,大都是涉及转换条款.在宏观经济中,利率应该是随机的,利率的升高会导致公司融资成本的提高进而影响公司的经营,导致公司违约率的上升.本文在约化模型框架下考虑了具有随机跳违约风险和利率风险的可转换债券的定价,综合利用风险中性定价原理和测度变换方法得到了可转换债券的解析定价公式,推广了相关文献的结果.基于合理的可转换债券定价,公司可转换债券的发行,投资者投资组合的优化和风险规避才更为切实可行.因此,本文的研究结果对可转换债券的定价具有重要的参考价值.

[1] BIELECKI T R, RUTKOWSKI M. Credit risk:Modelling,Valuation and Hedging[M].Berlin:Springer, 2002.

[2] INGERSOLL J E. An examination of corporate call policies on convertible securities[J].Journal of Finance, 1977, 32(2):463-478.

[3] BRENNAN M J, SCHWARTZ E S. Convertible bonds:valuation and optimal strategies for call and conversion[J].Journal of Finance, 1977, 32(5):1699-1715.

[4] TAKAHASHI A, KOBAYASHI T, NAKAGAWA N. Pricing convertible bonds with default risk:a Duffie Singleton approach[J].Journal of Fixed Income, 2001, 11(3):20-29.

[5] AYACHE E, FORSYTH P A, VETZAL K R. Valuation of convertible bonds with credit risk[J].Journal of Derivatives, 2003, 11(1):9-29.

[6] BIELECKI T R, CREPEY S, JEANBLANC M. Arbitrage pricing of defaultable game options with applications to convertible bonds[J].Quantitative Finance, 2008, 8(8):795-810.

[7] BIELECKI T R, CREPEY S, JEANBLANC M. Convertible bonds in a defaultable diffusion model[J].Progress in Probability, 2011, 65(2):255-298.

[8] HUANG J B,LIU J, RAO Y L. Binary tree pricing to convertible bonds with credit risk under stochastic interest rates[EB/OL].Abstract and Applied Analysis,[2013-03-21].Article ID 270467,1-8.http://dx.doi.org/10.1155/2013/270467.

[9] 王 伟, 赵奇杰. 带有违约风险的可转换债券的简约型定价[J].应用概率统计, 2013, 29(3):287-296.

[10] SU X N, WANG W S. Pricing options with credit risk in a reduced form model[J].Journal of the Korean Statistical Society, 2012, 41(4):437-444.

[11] WANG J P, CHEN X. Double exponential jump diffusion model for pricing convertible bonds[J].Mathematica Applicata, 2007, 20(1):6-11.

[12] 林 海, 郑振龙. 中国可转债发行的股权价值效应[J].商业经济与管理, 2006, 180(10):49-52.

[13] JARROW R, YU F. Counterparty risk and the pricing of defaultable securities[J].Journal of Finance, 2001, 56(5):1765-1800.

[14] 严加安. 金融数学引论[M].北京:科学出版社,2012.

[15] 朱 丹. Vasicek利率模型下可转换债券的鞅定价[J].华中师范大学学报(自然科学版), 2010, 44(1):25-28.

Pricing of convertible bond with jump default intensity

PAN Jian1,2, XIAO Qingxian1

(1.Business School, University of Shanghai for Science and Technology, Shanghai 200093;2.College of Mathematics and Computer Science, Gannan Normal University, Ganzhou, Jiangxi 341000)

In this paper, an issue of pricing convertible bonds pricing problem with double jump diffusion default intensity is studied under the reduced-form model. The jump sizes obey the double exponential jump diffusion process, and the price of a stock byob the time-varying diffusion model. The interest rate is governed by the Hull-White model as well as the pairwise correlation model. A pricing model is set up by applying risk-free equilibrium principle. Afterwards, the exact analytical solution of the pricing model is derived by using the martingale method, which extends the conclusion of related literature.

jump default intensity; Hull-White interest rate model; reduced-forms model; martingale method; pricing of convertible bond

2015-09-03.

国家自然科学基金项目(11471175).

1000-1190(2016)02-0159-09

O211.63;F830.9

A

*E-mail: pan79610@163.com.