基于滚动策略的不确定干扰下场桥调度问题研究

梁承姬，王典雪，徐德洪

(上海海事大学 科学研究院 物流研究中心，上海 201306)



基于滚动策略的不确定干扰下场桥调度问题研究

梁承姬，王典雪*，徐德洪

(上海海事大学 科学研究院 物流研究中心，上海 201306)

目前影响集装箱港口装卸效率的“瓶颈”从岸边作业转移到堆场作业.合理的场桥调度方案不仅可以提高堆场作业效率也可以配合集卡、岸桥，提高整个港口的装卸效率.而在实施场桥调度方案时，总会出现各种不确定干扰因素使得原先的方案不能正常实行.针对这一问题 ，本文提出一种在滚动窗口策略下处理不确定干扰因素的场桥调度流程，即当出现干扰时，触发窗口再调度机制，以减少干扰的影响.并且建立了以任务完成最大延迟量最小化为目标的混合整数规划模型，采用改进遗传算法对模型进行求解.通过案例分析对比，验证了算法的有效性以及滚动窗口策略下场桥调度方案更优，更符合港口的实际运营.

滚动窗口策略； 不确定干扰因素； 场桥调度； 改进遗传算法

集装箱码头是陆地和海上运输的连接点，并且作为多式联运的转运站和枢纽来进行服务[1].因此，对于任何一个集装箱码头来说，堆存效率以及在码头区的大量集装箱运输都是至关重要的.目前影响集装箱港口装卸效率的“瓶颈”从岸边作业转移到堆场作业.合理的场桥调度方案可以提高堆场作业效率，因此场桥调度问题的研究对于集装箱港口的作业管理具有重要意义[2].对于场桥调度工作，目前主要是依据场桥就近原则，工作量平衡原则，场桥调度员凭借经验进行调度，缺乏系统性.场桥调度问题对于集装箱码头的作业管理有着重要意义.本文将研究基于不确定因素下的场桥调度，为了达到优化调度方案，使得堆场作业效率提高从而提高码头作业效率的目的.

目前已有不少学者对场桥调度问题进行了研究.文献[3]和文献[4]讨论了场桥的动态调度问题，在最小化剩余工作量的目标下，确定场桥在箱区间移动的次数和路线.文中建立了混合整数规划模型，并采用启发式算法进行求解.模型的基本假设中考虑了场桥之间的干涉约束，设定每个箱区中最多只能有两台场桥同时工作，有效避免了调度的不必要麻烦，通过算例分析，验证了方法的有效性.文献[5]研究多台场桥的调度问题时，考虑了场桥间的干涉因素以及具有不同服务时间的任务集，并建立了整数规划模型.由于场桥调度问题为NP-hard问题，文章最后采用基于动态规划的启发式算法求解模型.计算结果表明，启发式算法能够有效地解决调度问题.以上文献在考虑场桥调度问题的时候，只考虑了场桥作业时的干涉因素(由于场桥体积大，多台场桥同时作业会出现“干涉”情况)，并没有考虑到实际作业中会出现的不确定干扰因素(比如，由于某船舶需要紧急离港，该船上的箱子需要紧急处理，这样，原先的场桥任务分配情况会受到干扰)，而在实际港口码头作业中，不确定的干扰因素是大量存在的，因此，本文将把不确定干扰因素考虑到场桥调度中来，企图得到更符合实际的调度方案.

文献[6]考虑了一种动态滚动策略的场桥调度决策方案，建立了最小化箱区内所有任务的延迟量以及场桥转场距离的整数规划模型，提出了一种结合仿真模型的启发式算法，并建立仿真模型以推进计划周期，对任务组的延误进行评估.同时，采用遗传算法对启发式算法得到的初始解进行优化.通过算例验证，提出的动态滚动策略更贴近于码头实际作业情况，比静态滚动方法得出更精确的调度方案.文献[7]进行了基于时间窗的场桥调度研究，利用干涉管理思想，解决场桥实际调度中产生的操作困难，得出相应的模型函数求得最优调度策略；其次，引入时间窗概念，通过设置理性的时间窗，构造带有时间窗的场桥调度函数模型，使整个场桥调度中存取箱作业尽量满足集装箱计划到达时刻表，减少存取箱作业的提前或延迟，以达到集卡等待时间最小化，最大化场桥利用效率.以上两篇文献，从设计滚动时段的角度，针对场桥调度，进行周期性的滚动更新，这比以往的静态调度得到更优良的调度方案；文献[6]采用遗传算法对启发式算法的初始解进行优化，验证该方法的有效性，而戴开梅则加入时间窗，运用启发式算法求解，虽然都取得有效成果，但两篇文献仍然没有将不确定干扰因素考虑进来，此外，两篇文献提出的是离散时间下的场桥调度问题，而场桥调度是实时调度，并且实时调度问题会经常出现new arrival moves handling，因此，本文将从连续时间角度考虑场桥实时调度问题.

文献[8]考虑了基于遗传算法的车间动态调度研究，考虑了车间作业在不确定因素影响下，进行滚动优化机制，利用改进遗传算法求解.实例证明，采用该方法可以使得车间作业效率大大提高.文献[9]对动态泊位调度引入滚动窗口技术，并采用Memetic算法进行计算求解得出较优的泊位调度方案，文中的Memetic算法结合了禁忌搜索和遗传算法求解，禁忌搜索用于局部搜索，遗传算法用于全局优化，算例证明了该算法在解决此问题时的有效性.文献[10]针对连续泊位与桥吊集成调度求解的困难，引入一种基于滚动策略的优化方法，将动态抵泊的船舶按照顺序分成若干连续的调度窗口，设计滚动窗口的滚动机制，采用启发式算法求解，通过算例分析说明利用滚动调度方法能有效解决大规模的调度问题.以上3篇文献都将滚动窗口策略引用到动态调度问题里面来，并得到较优的调度方案.滚动调度方法的主要思想在于，通过反复求解小规模优化问题来取代求解大规模调度问题，这样，将问题简化，同时得到更优解决方案.但是，这些思想目前还没有在场桥调度中得到运用；因此，本文将从连续时间角度考虑场桥实时调度问题，根据集装箱动态到达的顺序，将调度过程分为连续的调度窗口，将大规模的调度分解，引用滚动窗口策略方法，通过此方法解决场桥作业中的不确定干扰因素.基于前面有学者采用遗传算法求解验证了该算法在求解此类问题的有效性，因此，本文将继续用遗传算法求解.

1 问题描述

在场桥调度中，存在场桥来不及处理任务，集卡等待的情况，这造成了集卡资源的浪费，作业分配不合理也影响了集装箱码头的作业效率，从而降低了货物吞吐量.在实际集装箱码头作业中，存在许多不确定因素，比如：船舶到港时间的不确定会影响集装箱是否能按时被处理；场桥可能出现机械故障，不能及时对集装箱服务；集装箱延迟到达，但又急需处理等等因素.为了更好达到客户需求，本文引用“滚动窗口策略”来解决动态调度问题，当发生不确定干扰因素时立即重调度，如果未发生干扰因素，则进行之前设定的周期滚动调度.这样做目的是实现场桥实时调度，从而节省时间，使服务水平得到提高.场桥调度的流程如图1.

图1 场桥调度流程图Fig.1 The process of YC schedule

滚动窗口策略的工作原理为：在初始时刻，从所有待处理任务中选取一定数目的任务，加入任务窗口进行调度并产生初始调度方案，这是静态调度问题；但在初始方案的执行过程中，由于作业环境情况的变化，需要进行再调度，也就是动态调度；这时将已完工的任务从任务窗口中移去，再加入一批待处理任务到任务窗口中，重新对任务窗口内的任务进行静态调度.这样的过程重复进行，直到所有任务都完成，这就是滚动窗口调度策略.

滚动调度方法的主要思想是滚动优化，把不确定性调度问题分解成一系列动态但确定的调度问题，通过将动态调度过程分解成连续静态调度窗口，然后在线优化每个滚动窗口，使系统在此窗口内达到最优，再平移窗口并更新窗口中优化问题的参数，以此循环，直到所有任务完成.首先建立一个动态调度装卸任务窗口，窗口任务数量的选取根据集装箱码头实际的作业情况来确定，一般按照先到先服务的原则选取一定数量的任务加入到场桥调度窗口，对当前窗口下的任务建立数学优化模型，求解得出当前的场桥调度方案，并设定周期的滚动时间；当触发再调度机制的突发事件出现时，实施再调度.将已完成的任务从滚动窗口移除，并把需要紧急处理的任务移入滚动窗口，使当前窗口中的装卸任务数量保持一定的平衡，场桥进行任务再分配，不断的重复上述过程，直到所有的装卸任务全部完成.

假设设定周期性的再调度每间隔30 min调度一次，从0时刻开始，根据已到达场区任务以及任务处理优先权等原则，进行初始调度计划，各场桥进行任务安排，开始作业；随着任务的进行，到达的任务会发生变化，任务处理顺序也会发生相应变化，假设在时刻20 min时出现某紧急任务需要处理，时刻50 min该任务处理完成，那么，该系统调度时刻为20 min、30 min、50 min、60 min，以此类推，直到所有任务完成.图2即为任务受到干扰时的处理情况.

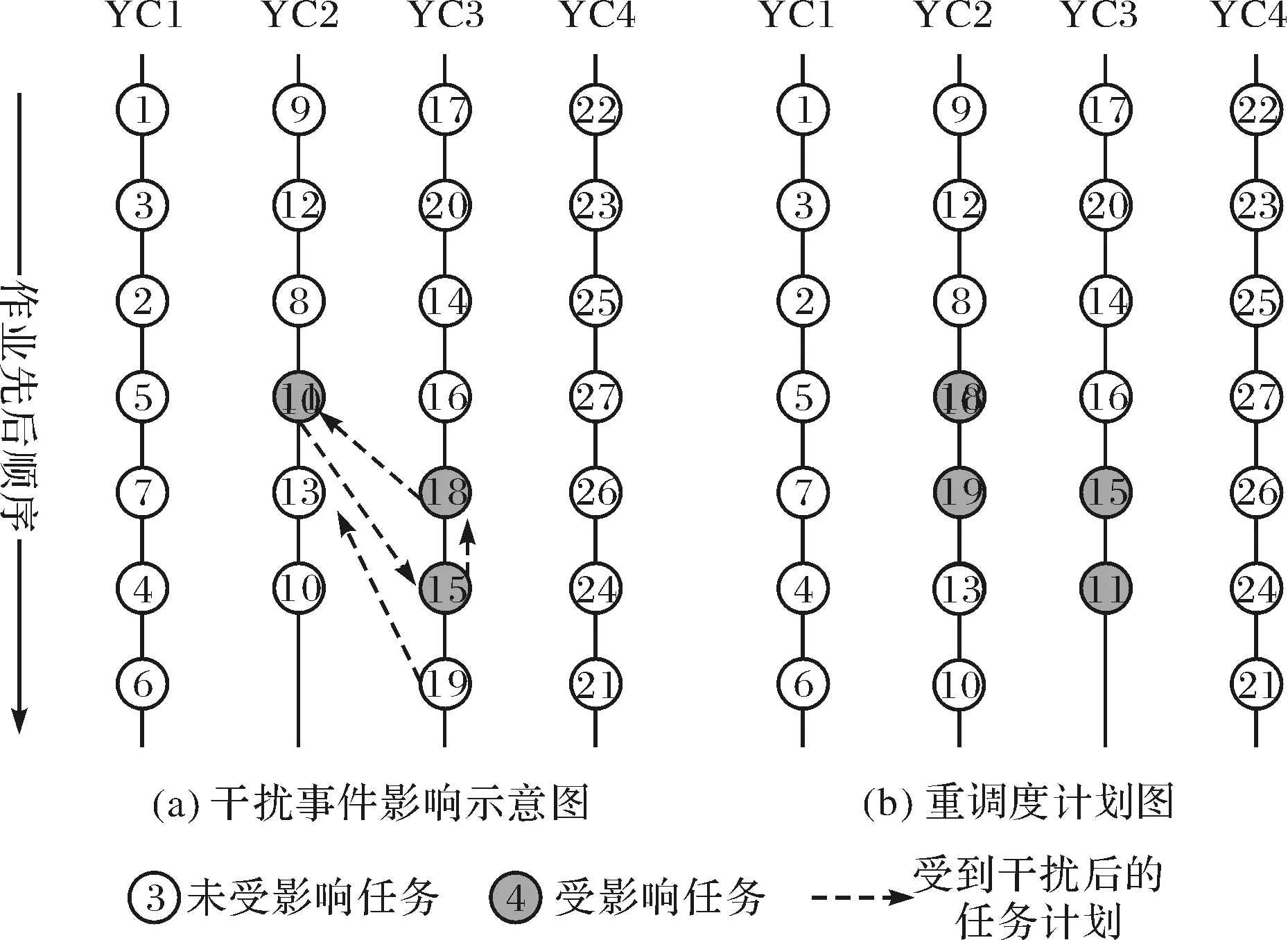
图2 处理干扰的调度示意图Fig.2 The dealing of the interference

当突发因素出现时，场桥应该优先处理干扰因素，此时应该暂时“封存”原先任务，进行重调度，当干扰因素处理结束，进行场桥重调度，直到任务完成.以需要紧急处理的集装箱为例.

由于船舶需要紧急离港，该船上的箱子需要及时处理.定义p1为正在作业的任务，p2为待入场任务，其具体步骤如下：

Step1：将需要紧急处理的任务安插到p1之后，同时暂时“封存”p2中的所有待处理的任务；

Step2：计算p1中所有任务的完工时间以及场桥的释放时间；

Step3：运用遗传算法进行调度，得到对于紧急处理任务的优化结果；

Step4：当紧急处理的任务被处理完毕后，p2中待处理任务的预期处理顺序和服务场桥已经不同.计算紧急处理的任务被安排之后所有场桥的可释放时刻；

Step5：运用遗传算法进行再调度，生成新的调度方案.

例如，图2中从上到下是场桥处理任务的顺序，每个圈代表一个任务，圈中的数字代表任务编号，其中，灰色为发生扰动计划的任务，图中虚线指任务的扰动计划.任务初始安排如图2(a)所示，由于任务进行到100 min时，任务15，16，18，19需要紧急处理，因此，应优先安排，此时，调用GA进行场桥重调度，以在规定时间完成紧急任务的前提下最小化任务延迟量为目标.原来任务11由YC2服务，重调度后置于任务15之后，由YC3处理；任务18，19则安插在YC2处理的任务8和任务13之间，任务13和10也相继往后移动.即重调度后YC2发生变化的任务处理顺序依次为18、19、13、10，而YC3处理完任务16后的任务处理顺序由原来的18、 15 、19变为15、11.得到的新调度方案，如图2中图(b)所示.其作业流程图如图3所示：

图3 滚动策略调用GA作业流程图Fig.3 The progress of rolling-horizon decision strategy using GA

2 模型建立

在每个时间窗内建立以任务完成最大延迟量最小化为目标的混合整数规划模型.本文研究的案例来自一个有4个箱区的堆场，集装箱均为20英尺，考虑4小时作业时段，数据来自于某港口码头实际业务数据.为避免场桥作业中出现干涉，假设单个箱区内同时作业的场桥数不超过两台；滚动策略为每小时滚动一次，突发干扰因素只考虑紧急任务情况；每个时段场桥的任务数量不应该超过场桥从当前时间到计划完成时间的工作能力.前期未完成的任务仍然被视为一个新的任务，该任务的到达时间即为当前滚动周期的开始时间.假设场桥在平行场区间的移动距离按箱区长度计算，在垂直区间的移动设定所有转弯以及垂直行驶时间固定为3*3.5 min；假设场桥完成一次move(一次存箱或取箱任务)的时间是3 min；无突发干扰因素发生时，每台场桥在一个时段内只能在某一箱区服务，且场桥必须处理完当前任务才能处理下一个任务.

2.1 基本假设

1) 堆场内用于卸装作业的场桥型号、司机水平等相同，确保场桥作业效率一致；

2) 集卡运行速度，场桥作业效率均一致；

3) 一个任务组的集装箱放到同一箱区，来自于同一船舶；

4) 场桥在完成集装箱任务过程中，集卡的配置数目是充足的；

5) 所有场桥在同一计划时间段，同时开始和结束该时段的作业.

2.2 参数设计

NP：计划时间域内计划时间段总数；

NTt：t计划时段内集装箱任务组数量；

NTit：t计划时间段内集装箱任务组中包含的集装箱任务数量i；

Bit：t计划时间段内集装箱任务组所在的箱区；

Nc：当前计划时间段内的新任务组数量；

j： 新的集装箱任务组；

S： 箱区s的可用容量；

M：需要作业的集装箱集M={1，2，…，m}；

NC：场区中可用的场桥总数；

k： 场桥k编号；

NTj：当前计划时间段内新任务组j里的任务数量；

TPit：t计划时间段内集装箱任务组i的计划完成时间；

TRit：t计划时间段内集装箱任务组i的实际完成时间；

TPj：当前时段新任务组j的计划完成时间；

TRj：当前时段新任务组j的实际完成时间；

v： 场桥作业效率；

2.3 决策变量

如果场桥k在t时段内分配给集装箱任务i，xikt=1；否则，xikt=0.

如果集装箱任务i放到箱区s，yis=1；否则，yis=0.

2.4 约束条件

j=(1，2，…，NC)，

(1)

i=(1，2，…，NTt)，

(2)

Tli-Tai>0，

(3)

(4)

(5)

i∈(1，2，…，NTt)， t=(1，2，…，NP)，

(6)

(7)

(8)

xikt=0 or 1， t=(1，2，…，NP)，

i=(1，2，…，NTt);k=(1，2，…，NC)，

(9)

TBiot=0 or 1， t=(1，2，…，NP)，

i=(1，2，…，NTt); o=(1，2，…，NTt)，i≠0.

(10)

约束条件(1)表示任意时段内，一台场桥只能同时服务一个集装箱任务组；(2)表示任意时段内，一个集装箱任务组有且只有一台场桥服务；(3)表示每个集装箱任务组必须在集卡到达箱区后才开始被服务；(4)表示需要存放的集装箱总数不大于堆场容量；(5)表示当前时段内总的任务数量等于每个时段内任务数量和；(6)表示任意时段，同一场区同时作业的场桥数不超过两台 ；(7)表示任何时段内被分配作业的场桥数量不大于总的场桥数量；(8)表示场桥工作能力不超过集装箱任务数量；(9)、(10)均是二进制表示.

2.5 目标函数

(NTi(t-1)-NTit)v，

(11)

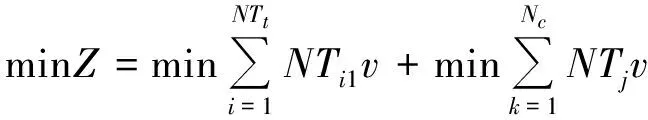
(12)

(13)

(11)是目标函数，旨在求滚动计划时段内的任务完成时间的延迟量最小.(12)指当前滚动时段内总的计划任务量；(13)指当前滚动时段总的任务完成量.

3 算例分析

3.1 遗传算法

场桥调度问题是一个NP难的问题，计算复杂度很高，很难用现有的研究技术在合理时间内获得满意的解.在解决场桥调度问题时，以往的研究中有采用模拟退火算法，禁忌搜索算法以及启发式算法等方法求解的，而对于滚动策略来说，使用启发式算法计算量太大，根据参考文献有学者采用遗传算法求解并得到较好结果，因此，本文考虑使用改进的遗传算法来解决该问题.下面是对遗传算法的具体解决方案解释.

3.1.1 染色体编码 本文采用的是二维编码，分别表示场桥作业顺序，以及场桥的任务组作业量.染色体采用整数形式编码.具体形式如下.

图4 染色体编码Fig.4 The chromosome encoding

染色体编码可理解为：若场桥j在任务i的作业顺序是0，表示场桥j不服务任务组i；此时，该基因处的作业量即为0.每条场桥染色体的长度为NT1+Nc.该染色体表示：场桥1给任务组3服务，作业量为20个move(move为场桥作业量的单位，表示场桥经过一次起重和落重，完成一次装卸任务)，场桥2先为任务组1完成24个move，再给任务组2完成35个move.

3.1.2 种群初始化 种群初始化方法如下流程图所示，假设种群规模为n，也就是说，要形成完整的种群，需要将该方法重复n次.

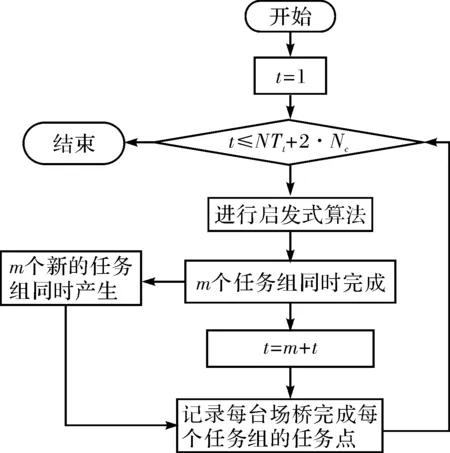
图5 种群初始化Fig.5 The population initialization

3.1.3 适应度函数 适应度函数的公式如下：

(14)

目标函数值越小，适应度函数值越小，个体适应度越高.

3.1.4 父代选择 父代选择的步骤为

Step3：计算个体的累计概率.

Step4：产生n个0到1之间的随机数.

Step5：如果随机数落在两个个体的累积概率之间，则选择累积概率较高的那个个体.

3.1.5 遗传算子设计 遗传算子设计步骤如下.

1) 选择

为了减少整个程序运行时间，本文考虑选择算子采用较简单的随机遍历选择策略.具体操作像轮盘赌一样计算选择概率ps，只是随机遍历选择法中等距离的选择体，如图6所示，设newpoint 为需要选择的个体数目，进行等距离的选择个体，选择指针的距离是1/newpoint ，第一个指针的位置由[0，1/newpoint ]的均匀随机数决定.

图6 随机遍历选择法Fig.6 The method of random traversal selection

本文采用整数编码，一般整数编码采用普通的单点交叉或者多点交叉方式.为了更好地控制修正发生的概率和修正幅度，本文设计一种基于滑动窗口的两点交叉算子，其具体思想如下.

Step1： 选取两个个体作为父代，在选取的父代中按设定的滑动窗口大小内随机确定两个交叉点，形成一个交叉的基因片段窗口，基因片段为不超过设定的滑动窗口大小的连续基因组成，如图7所示.

交换后发现有重复基因(图中阴影部分标出)；

图7 根据设定窗口大小选择基因片段Fig.7 According to the setted window size selecting gene

图8 交换基因后的染色体Fig.8 The chromosome after exchanging gene

图9 重复基因修正流程图Fig.9 The progress of gene repair

图10 修正过后的子染色体Fig.10 The repaired chromosome

2) 变异

为了避免算法陷入局部最优，设计合理的变异算子使得增加后代多样性.本文设计了一种非线性变异算子进行染色体变异，表达式为

Offspring=

上式中，A和B分别是变异的上限和下限，r是0到1之间的一个随机数，N为种群当前的迭代次数，M为种群的最大迭代次数，c为变异的调节参数.场桥作业顺序的变异范围是[0，NT1+Nc].计划周期开始时已有任务组的作业量变异范围为[0，NTi1]而周期内新出现任务组的作业量变异范围为[0，NTk].此外，若染色体某基因的作业顺序维为0，则其任务组作业量维也必须为0.

3.1.6 基因修复 在交叉与变异完成后，有可能产生不可行后代，此时需要进行用基因修复.本文设计的基因修复具体规则如下：

规则1 如果场桥j被分配给任务组i，但此时另外一台场桥正在对任务组i服务，那么场桥j应该被分配给其他没有场桥作业的任务组.

规则2 如果场桥j被分配给任务组i，但此时已经有两台场桥在任务组i所在的箱区作业，那么场桥j应该被分配到另一个任务组，且该任务组所在箱区正在工作的场桥数不大于1.

3.1.7 子代接收策略 在交叉、变异和基因修复完成后，将所有的后代按照适应值排列，并将序号大于种群规模数的后代舍弃.

3.1.8 终止条件设定 当算法的迭代次数达到最大迭代次数时，算法终止.算法的最大迭代次数由实验决定.

3.2 算例分析—以突发紧急任务为例

本文算例基于一个在4个箱区具有4台场桥对27个任务组的作业的情景，算例在可作业时间为240 min的时段内进行，在MATLAB上用遗传算法进行求解.算例输入数据见表1所示.

表1 算例初始数据

表1中，TN指任务组编号，Slot指任务目标堆存位置，PT指任务组准备时间，V指每个任务组包含任务量.首先，进行无干扰情况下的周期驱动的滚动窗口策略的算例，在MALAB上用遗传算法求解得到的任务分配方案如图11所示.

图11 无干扰情况下场桥调度方案Fig.11 YC schedule without interference

由上图，可直观看到，在无干扰情况下，实施周期驱动的滚动策略调度方案，对任务进行合理安排，使得每个滚动窗口内的目标函数最优，使每个窗口内延迟量最小，该方案下，所有任务完成时间为228 min，图中M指任务组，M右边第一个数字指所在箱区，后两位数字代表箱子存放位置，图中从左向右即为场桥服务的顺序.

本文考虑一种基于急件插入情况的突发干扰因素，某时刻由于船舶急需离港，该船上的集装箱急需处理，此时，应该将属于该船上的任务作为紧急任务插入，调整场桥分配，重新安排任务.算例设定滚动计划为60 min进行一次周期滚动，同时，突发任务出现时进行重新调度，定义同一个箱区内的可以集中装卸的多个任务为一个任务组，任务组作为场桥作业的最小化单位，场桥一次作业叫做一个move.下面进行有干扰情况的算例分析.

由于在任务进行到第100 min时，来自箱区3的任务组15，16，18，19需要在一个小时后处理完，因此进行紧急处理，此时发生重调度计划，因此，第二次滚动的调度方案受到干扰，进行重调度后的调度方案和无干扰情况进行对比可知，场桥2和场桥3发生重调度，场桥2和场桥3作业路径分别为：

M207⟹M217⟹M201⟹M314⟹

M316⟹M220⟹M210；

M311⟹M318⟹M303⟹M309⟹

M305⟹M212.

而在无干扰情况下，场桥2和场桥3的作业路径分别为：

M209⟹M212⟹M208⟹M211⟹

M213⟹M210；

M317⟹M320⟹M314⟹M316⟹

M318⟹M315⟹M319.

在满足紧急任务按时完成并使得所有任务完成时间最短，任务延迟量最小的情况下，得到如图12所示的场桥调度方案，该方案下所有任务完成最短时间为213 min.

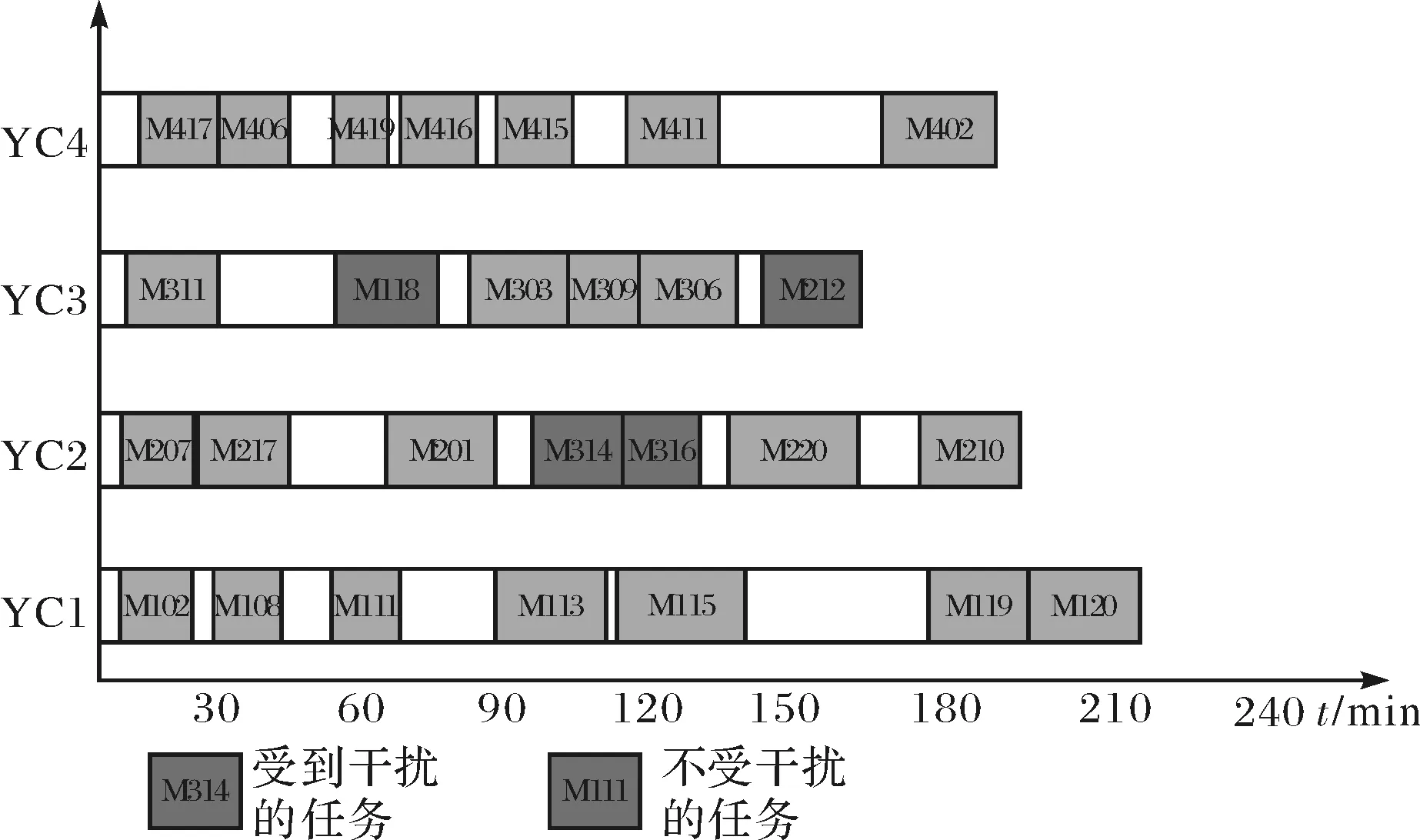
图12 有干扰情况下场桥调度方案Fig.12 YC schedule with interference

4 结论

本文针对场桥动态调度中，由于不确定干扰因素的影响，导致原先的调度方案发生变化这一问题进行研究，提出滚动窗口策略来解决该问题，当突发因素发生时，及时调整调度方案，算例证明，滚动策略能有效解决该问题，由于滚动策略进行的是每个滚动窗口中的优化，从而来实现全局的优化，这种方案能够节约计算时间，适用于大规模的问题.本文采用改进的遗传算法，利用MATLAB来求解场桥调度模型.

[1] LI W，WU Y，PETERING M E H，et al. Discrete time model and algorithms for container yard crane scheduling [J]. European Journal of Operational Research，2009，198(1): 165-172.

[2] STAHLBOCK R，VOΒ S. Operations research at container terminals: a literature update[J]. OR Spectrum，2008，30(1):1-52.

[3] ZHANG C Q，WAN Y W，LIU J Y, et al. Dynamic crane deploymention container storage yards[J]. Transportation Research Part B，2002，36(6):537-555

[4] RICHARD J, LIN N, ZHANG C Q. A heuristic for dynamic yard crane deployment in a container terminal[J]. IIE Transactions，2003，35: 161-174

[5] HG W C. Crane scheduling in container yards with inter-crane interference[J]. European Journal of Operational Research，2005，164: 64-78

[6] CHANG D F，WEI Y ，JIANG Z H ，et al. Developing a dynamic rolling-horizon decision strategy for yard crane scheduling[J]. Advanced Engineering Informatics，2011，25: 485-494．

[7] 梁承姬，戴开梅. 基于集装箱任务组时间窗的堆场场桥调度模型建立与求解[J].河南科学，2013，31(4): 477-483．

[8] 张富生，刘长安. 基于遗传算法的车间动态调度研究[D].山东：山东大学，2013．

[9] 林志国，王 诺. 基于滚动窗口的集装箱码头泊位动态调度研究[D].辽宁：大连海事大学，2010．

[10] 肖 玲，胡志华. 基于滚动策略的集装箱码头连续泊位与桥吊集成调度[J].计算机应用，2013，33(10)：2969-2973．

[11] HE J L，CHANG D F，WEI J, et al. A hybrid parallel genetic algorithm for yard crane scheduling[J]. Transportation Research Part E，2010，46: 136-155．

[12] 严 伟，宓为建，苌道方，等. 一种基于最佳优先搜素算法的集装箱堆场场桥调度策略[J].中国工程机械学报，2008，6(1):95-100．

[13] KIM H K，LEE M，WANG H H.Sequencing delivery and receiving operations for yard cranes in port container terminals[J]. International Journal of Production Economics，2003，84(3):283-292．

[14] LI W K，WU Y，PETERING M, et al.A continuous time model for multiple yard crane scheduling with last minute job arrivals[J]. Int J Production Economics，2012，136: 332-343．

[15] 刘文君. Memetic算法研究与工程应用[D]. 武汉：华中科技大学，2007．

Research of the yard crane schedule with uncertain interference that based on the rolling-horizon decision strategy

LIANG Chengji，WANG Dianxue，XU Dehong

(Logistics Research Center，Scientific Research Academy，Shanghai Maritime University，Shanghai 201306)

Currently，the “bottleneck” affecting the efficiency of container port handling was transferred from the berth to the yard. A reasonable yard crane schedule can improve the efficiency of yard work，so the research of yard crane schedule has an important effect on the management of container ports. Based on the uncertain interference factors in the yard crane operation，a dynamic rolling-horizon decision strategy was proposed to deal with the problem that how to reduce the uncertain interference factors and thus improve efficiency of yard crane. A mixed integer programming model was established to minimize the maximum delaying time at blocks and the improved Genetic algorithm was used to solve the model. According to the analysis of examples，this algorithm is useful and the dynamic rolling-horizon decision strategy is effective in scheduling the yard crane under uncertain interference factors．

rolling-horizon decision strategy; uncertain disturb factors; yard crane schedule; improved genetic algorithm

2016-04-22.

国家自然科学基金项目(71471110,71301101);上海市科委项目(14170501500).

1000-1190(2016)05-0695-09

F512.5

A

*通讯联系人. E-mail: wangdianxue519@519.com.