“互联网+”背景下电子废弃物双渠道回收策略研究
2016-11-29许晓彬朱小林
许晓彬,杨 斌,朱小林
(上海海事大学 物流研究中心,上海 201306)
“互联网+”背景下电子废弃物双渠道回收策略研究
许晓彬*,杨 斌,朱小林
(上海海事大学 物流研究中心,上海 201306)
在“互联网+”背景下,基于生产商委托互联网回收商和专业拆解公司回收的双渠道回收模式,构建了生产商、互联网回收商及专业拆解公司组成的闭环供应链博弈模型.分别分析了在集中决策和分散决策下闭环供应链各成员的定价策略.同时进一步分析了在分散决策情况下,互联网回收商的转让定价策略.最后通过数值算例,比较了这两种决策下的最优定价及供应链系统收益情况,并且分析了转让价格系数对供应链系统收益的影响.
“互联网+”回收模式; 逆向物流; 博弈论; 双渠道回收
统计数据显示,2014年全球共产生4 180万t电子垃圾,中国以603万t稳居世界第二.随着工业化浪潮席卷全球,电子垃圾已成为世界上增长最快的垃圾.据工信部的数据显示,目前,中国手机、计算机、彩电等主要电子产品年产量超过20亿台,每年主要电器电子产品报废量超过2亿台,重量超过500万t,中国已成为世界第一大电器电子产品生产和废弃大国.根据《中国国家标准·物流术语》(GB/T 18354—2001),将逆向物流分为回收物流和废弃物物流两大类.本文研究主要是针对电子废弃物的回收,属于废弃物物流.
“十一五”时期以来,国家采取一系列措施,大力推动循环经济发展,再生资源回收的理念渐入人心.为贯彻落实党的十八大和十八届三中、四中全会精神,大力推进生态文明建设,发展循环经济,国家制定了《再生资源回收体系建设中长期规划(2015——2020年)》.规划中强调大力发展的重点工程之一为回收模式创新工程.提出重点品种回收模式创新,以及企业回收模式创新.实现面向全社会的第三方回收模式,积极探索、创新各种行之有效回收模式.本文研究中提到的互联网回收商回收模式正是当前社会一种创新回收模式.
国内外学者对逆向物流及闭环供应链以进行了一系列的研究.SAURABH等[1]研究发现目前对逆向物流的研究在不断变化,主要研究有关预测产品退货、外包等问题,处理决策没有被广泛研究.KANNAN等[2]通过对现有文献的分类、分析,提出了逆向物流及闭环供应链未来研究方向.PIETRO和GEORGE[3]构建了两阶段闭环供应链博弈模型,讨论了制造商回收外包策略对制造商和零售商或者第三方回收商的影响.TIAN Yihui等[4]构建了系统动力学模型并采用演化博弈论方法研究了政府补贴政策对中国绿色供应链管理的影响.MA Junhai和WANG Hongwu[5]构建了产品回收的闭环供应链动态非合作博弈模型,并分析了系统回收的复杂性.MAHESHWAR等[6]以印度作为案例,使用经济模型以确定不同的EPR召回方案的盈利能力并评估其是否符合印度的条件.
国内外也有一些学者对电子废弃物回收,特别是回收渠道方面进行了研究.BERK等[7]研究考虑不确定性的逆向物流网络设计的第三方电子废弃物回收企业利润最大化问题.于春海和李想[8]运用博弈论方法研究了双渠道回收模式下,基于分散决策和集中决策的闭环供应链的定价机制与协调策略,并研究了系统回收效率.谢磊和马军海[9]构建了基于消费者效用最大化的复杂动力学模型,分析了“网络回收认可程度”对回收渠道利润和系统稳定性的影响.HUANG Min等[10]研究了制造商负责生产,零售商负责销售,同时零售商和第三方回收双方商竞争回收的双渠道闭环供应链定价策略.MA Wei-min等[11]研究了政府补贴政策对双渠道回收闭环供应链成员的决策影响.LI Bo等[12]运用博弈模型研究了集中决策、分散决策情况下,单渠道回收和双渠道回收模式下供应链各成员的定价及环保策略.
随着互联网技术的发展,电子商务模式和网络支付技术的逐渐成熟,以及电子废弃物回收在“互联网+”的探索,回收市场上逐渐兴起了互联网回收模式.本文研究了生产商委托互联网回收商和专业拆解公司回收的双渠道回收模式下,这三方利益主体在集中决策及分散决策下的定价决策问题;同时研究了在分散决策情况下互联网回收商的转让定价决策问题.
1 模型描述
1.1 问题描述
互联网回收商通过互联网回收平台,整合线上及线下资源.对所有回收来的产品进行质检、评级,依据评级结果执行不同的处理方式:一部分产品交由合作的正规专业拆解公司进行环保降解;另一部分产品经过专业的维修、翻新后,通过网上二手交易平台销售,同时提供售后保修服务.正规专业拆解企业通过自己在城市以社区和办公楼宇建立的线下回收渠道进行回收.这样就形成了生产商委托互联网回收商和专业拆解公司回收的双渠道回收模式.同时,专业拆解企业自身回收渠道与互联网回收商回收转让渠道一起也组成了专业拆解企业的双渠道回收模式.闭环供应链系统流程图见图1.

图1 闭环供应链系统流程图Fig.1 The flow chart of closed-loop supply chain system
1.2 基本假设与符号说明
根据问题分析需要作如下假设.
假设1:电器电子产品生产者、进口电器电子产品的收货人或者其代理人依法按照《废弃电器电子产品处理基金征收使用管理办法》的规定履行基金缴纳义务,单位产品处理基金为Te.国家对于纳入废弃电器电子产品处理基金的正规专业拆解企业进行财政补贴,单位处理产品财政补贴为f.
假设2:假设生产商完全采购新的原材料和零部件生产新产品的单位成本为Mc,部分原材料和零部件使用回收拆解企业的可再利用原材料及零部件的生产单位成本为Mr,显然Mc>Mr>0.假设节约的单位生产成本为Ms,生产商回收拆解企业的可再利用原材料及零部件的单位成本为Pm,显然Ms=Mc-Mr,0 假设3:当前市场消费者对新产品和再制造品的需求为售价Pc的非线性减函数[11]: (1) 其中,D0为市场容量,α为新产品、再制造品的市场需求对其销售价格的敏感系数. 假设4:本文为简化模型,假设理想化的情况,假设生产商完全采购新的原材料和零部件生产新产品与采用从拆解企业回收的可再利用原材料及零部件生产的再制造产品在质量、功能和效用上是一致的,销售价格都为Pc,消费者对这两种产品的消费态度也是一致的. 假设5:Pi与Pp分别为互联网回收商与专业拆解企业的回收价格,互联网回收商与专业拆解企业在废旧品回收市场上竞争回收,一方的回收价格会影响到另一方的回收量,设互联网回收商与专业拆解企业的回收量分别为: Rir=R0+γPi-μPp, (2) Rpd=R0+γPp-μPi, (3) 其中,γ为消费者回收价格的敏感系数,μ为回收竞争系数,γ>μ>0,且R0表示消费者愿意无偿返还废旧产品的数量,代表了消费者的环保意识水平. 假设6:供应链系统上各成员之间产生的运输及管理成本不予考虑.同时,只考虑单周期闭环供应链的情况,忽略前期对后期的影响. 除了上述基本假设提到的相关参数,特此补充以下参数符号的说明. Rt:互联网回收商和专业拆解企业回收量总额; Rd:互联网回收商及专业拆解公司回收产品中最终进行拆解的数量; 2.1 利润函数 首先,生产商的收入为销售电子电器产品的销售额,使用再利用的原材料、零部件进行再制造产品而节约的成本;生产商的成本为销售成本、对没有进行回收处理的退出市场的产品所缴纳的环境税、向拆解公司回收再利用原材料及零部件的费用.因此生产商的利润可以表示为: (4) 其次,互联网回收商的收入为将回收的电子电器产品转入二手市场的销售额以及将回收的电子电器产品转让给专业拆解公司所得;互联网回收商的成本为其回收成本以及在二手市场销售产品给消费者后提供的售后保修服务的成本.因此互联网回收商的利润可以表示为: πIR= KsRirPs+KcRirλPi-KsRirCis- (5) 最后,正规专业拆解公司的收入为把拆解后得到的可再利用的原材料、零部件卖给生产商所得以及国家对进入国家补贴目录的正规专业拆解公司的拆解补贴;正规专业拆解公司的成本为回收成本、从互联网回收商转让回收产品的转让成本、拆解回收产品的拆解成本以及对拆解后不能再利用的废弃物的处置成本.因此正规专业拆解公司的利润可以表示为: KcRirλPi-RdCdc-KdRdPd. (6) 2.2 系统集中决策下策略分析 在集中情形下,生产商回收拆解企业再利用零部件及原材料的价格和互联网回收商转让回收产品的价格是系统内部参数,不影响系统整体决策.生产商通过市场需求预测确定产品的零售价以及联合互联网回收商和专业拆解企业联合确定回收价格以期整个闭环供应链系统利润最大化.在生产商、互联网回收商和专业拆解企业联合定价下,该闭环供应链的定价决策问题可以用如下优化问题来描述: (7) (8) 运用LINGO求解,得到供应链各方最优决策及供应链整体利润的最大值: (9) (10) (KrMs-Cdc-KdPd+f-Cpd- ((KrMs-Cdc-KdPd+f)Kc+KsPs- (11) 2.3 系统分散决策下策略分析 在分散决策情况下,生产商、互联网回收商和专业拆解企业均为理性独立的决策者,都会以自身利润最大化为目标进行决策.三者关系为一主多从的Stackelberg博弈关系,且生产商是领导者,互联网回收商和专业拆解企业是跟随者.首先,生产商在掌握消费者需求情况后确定产品(新产品与再造品)的销售价格及对拆解企业的再利用材料和零部件的回收价格.在完全信息对称条件下,互联网回收商和专业拆解企业掌握消费者供给情况后确定废旧品的回收价格.紧接着,互联网回收商以既定的价格从消费者手中回收废弃产品,并以一定的价格将回收产品转让给专业拆解企业. 互联网回收商可采取以下4种转让定价策略: 由于该博弈为完全信息动态博弈,其均衡是子博弈精炼纳什均衡,因此可以采用逆向归纳法来求解由此建立的定价决策模型(以平衡定价策略为例): (12) (13) KcRirλPi-RdCdc-KdRdPd, (14) (15) 解得分散决策情况下互联网回收商采取平衡定价策略时的最优转让价格系数及供应链各方最优定价策略: (16) (17) (18) (19) 同理可求分散决策情况下互联网回收商分别采取单渠道回收定价策略、最小化定价策略以及最大化定价策略时的最优转让价格系数和供应链各方的最优定价策略. 根据上述模型及求解结果,通过以下算例分析比较不同策略情形下闭环供应链各方的最优定价、回收量及收益情况,以及转让价格系数对系统运作的影响.对国内某微型计算机生产商,某回收网站以及纳入回收补贴目录的某专业拆解企业进行调研及分析其历年统计数据,相关参数取值如下: Mr=800,Mc=1500,Ps=600, Ks=0.6,Kc=0.4,Cir=35, Cis=22,Pd=26,Kr=0.7, Kd=0.3,Cpd=48,Cdc=27. 参考《废旧电器电子产品回收处理管理条例》对于回收补贴及处理基金的相关规定,以微型计算机回收为例,Te=10,f=85.其他相关参数取值如下: α=0.7,γ=0.8,μ=0.3, D0=10000,R0=100. 由上述模型求解结果及参数设置可以得到集中决策、分散决策下互联网回收商采取平衡定价策略时供应链各方最优定价和收益情况,见表1. 表1 不同决策情况下供应链各方最优定价及收益情况表 通过表1计算结果可以得出以下结论:生产商在集中决策下的销售价格低于分散决策下互联网回收商采取平衡定价策略时的销售价格,销售量正好相反;集中决策下供应链的整体利润总是大于分散决策下互联网回收商采取平衡定价策略时的整体利润;互联网回收商和专业拆解企业集中决策下的回收价格高于分散决策下互联网回收商采取平衡定价策略时的回收价格. 同时,运用MATLAB分析分散决策下转让价格系数对系统收益的影响,见图2. 图2 分散决策下转让价格系数对系统收益的影响Fig.2 The coefficient of transfer price influence on the supply chain system profit 图2中,阴影区域为单渠道定价策略,点a处为最小化定价策略,点c处为最大化定价策略,点b处为平衡定价策略的最优转让价格系数.通过图2可以看出:互联网回收商采取单渠道定价策略时供应链整体利润最低.分散决策情况下互联网回收商采取平衡定价转让策略时,供应链整体利润随着转让价格系数的增加而增加,并且在最优转让价格系数处达到最大,随后则随着转让价格系数的增加而减少. 研究发现,生产商在集中决策下的销售价格低于分散决策下互联网回收商采取平衡定价策略时的销售价格,销售量正好相反;集中决策下供应链的整体利润总是大于分散决策下互联网回收商采取平衡定价策略时的整体利润;互联网回收商和专业拆解企业集中决策下的回收价格高于分散决策下互联网回收商采取平衡定价策略时的回收价格.分散决策情况下,互联网回收商采取单渠道定价策略时供应链整体利润最低.互联网回收商采取平衡定价转让策略时,供应链整体利润随着转让价格系数的增加而增加,并且在最优转让价格系数处达到最大,随后则随着转让价格系数的增加而减少.研究成果对于企业创新回收模式及本文涉及的闭环供应链各成员的管理决策具有实际指导意义.本文研究中供应链为单个生产商、单个互联网回收商、单个专业拆解企业,新产品与再造品是同质的,具有一定局限性.未来可以进一步考虑多个供应链主体,需求的不确定性,新产品与再造品异质,信息不对称性等情况. [1] SAURABH A,RAJESH K S,QASIM M. A literature review and perspectives in reverse logistics[J]. Resources,Conservation and Recycling,2015,97:76-92. [2] KANNAN G,HAMED S,DEVIKA K. Reverse logistics and closed-loop supply chain: A comprehensive review to explore the future[J]. European Journal of Operational Research,2015,240(3):603-626. [3] PIETRO D G,GEORGES Z. A two-period game of a closed-loop supply chain[J]. European Journal of Operational Research,2014,232(1):22-40. [4] TIAN Y H,KANNAN G,ZHU Q H. A system dynamics model based on evolutionary game theory for green supply chain management diffusion among Chinese manufacturers[J]. Journal of Cleaner Production,2014,80(1):96-105. [5] MA J H,WANG H W. Complexity analysis of dynamic noncooperative game models for closed-loop supply chain with product recovery[J]. Applied Mathematical Modelling,2014,38(23):5562-5572. [6] MAHESHWAR D,PRATIK S. Modeling and assessment of e-waste take-back strategies in India[J]. Resources,Conservation and Recycling,2015,96:11-18. [7] BERK A,BERSAM B,NEZIR A. Stochastic reverse logistics network design for waste of electrical and electronic equipment[J]. Resources,Conservation and Recycling,2015,104(Part B):391-404. [8] 于春海,李 想. 闭环供应链双渠道回收系统定价机制与协调策略[J].东北大学学报(自然科学版),2014(9):1360-1363+1368. [9] 谢 磊,马军海. 中国废旧家电回收市场稳定性及其应用研究[J].复杂系统与复杂性科学,2015(3):96-109. [10] HUANG M,SONG M,LOO H L,et al. Analysis for strategy of closed-loop supply chain with dual recycling channel[J]. International Journal of Production Economics,2013,144(2):510-520. [11] MA W M,ZHAO Z,KE H. Dual-channel closed-loop supply chain with government consumption-subsidy[J]. European Journal of Operational Research,2013,226(2):221-227. [12] LI B,ZHU M Y,JIANG Y S,et al. Pricing policies of a competitive dual-channel green supply chain[J]. Journal of Cleaner Production,2016,112(3):2029-2042. Research on dual-channel recovery strategy of E-waste under “Internet+” background XU Xiaobin,YANG Bin,ZHU Xiaolin (Logistics Research Center,Shanghai Maritime University,Shanghai 201306) With the development of the “Internet+”,a dual-channel recycling model that product recycling was determined by the Internet recycler and professional dismantling enterprise have formed. A closed-loop supply chain game model consisting of the manufacturer,Internet recycler and professional dismantling enterprise was investigated. In centralized decision-making and decentralized decision-making are analyzed respectively under the pricing strategy of closed-loop supply chain members. Further analysis about the transfer pricing strategy of Internet recycler in the case of decentralized decision-making have done. Finally,a numerical example compares the two decision-making under the optimal pricing and supply chain system profit situation,and analyzes the coefficient of transfer price influence on the supply chain system profit. “Internet+” recovery mode; reverse logistic; game theory; dual-channel recovery 2016-01-17. 国家自然科学基金项目(71171129); 交通运输部科技项目(2015328810160); 上海市科委科研计划项目(14DZ2280200,14511107402). 1000-1190(2016)05-0683-06 F274; F224.32 A *E-mail: zsxxbdyx@163.com.

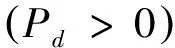

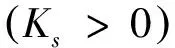
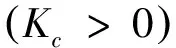







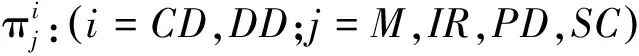
2 模型建立及求解







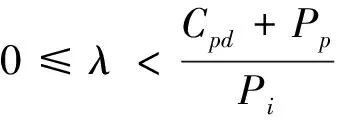







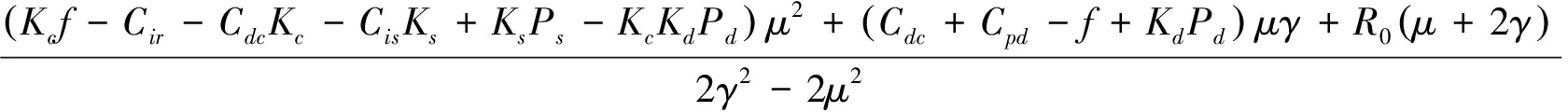


3 数值分析


4 结论
