双机器人协调的运动学分析

于广东，陈 琦

（中国科学院 长春光学精密机械与物理研究所，长春 130000）

设计与应用

双机器人协调的运动学分析

于广东，陈 琦

（中国科学院 长春光学精密机械与物理研究所，长春 130000）

根据双机器人协调运动学关系，将双机器人协调分为两类，并以双机器人协调焊接任务为例，根据任务要求分析双机器人系统相对运动协调的运动学关系，并进行了仿真验证，仿真结果表明文章所提出的双机器人协调运动关系的正确性。

双机器人；协调；运动学分析

0　引言

工业机器人已经广泛应用到工业生产的各行各业，随着工业生产对生产工具要求的提高，单个机器人越来越不能满足生产的需求了，因此双机器人系统逐渐成为机器人领域的研究热点，各国学者纷纷展开对双机器人系统的研究，研究的内容涉及到各个领域。分析确定两台机器人在特定任务下的运动学约束关系是双机器人系统进行控制的核心。

1　双机器人系统运动分类

根据双机器人系统中两台机器人末端位姿之间的关系，可以将双机器人运动协调分为以下两类，如图1所示。

图1　双机器人协调的分类

1）双机器人同步运动协调：如图1(a)所示，两台机器人之间存在一定的协调关系，在运动期间，两机器人末端的相对位姿关系保持不变，两机器人之间同步性很强。双机器人协调搬运便是典型的同步运动协调。

2）双机器人相对运动协调：如图1(b)所示，双机器人系统中的两台机器人末端不但存在位姿约束，而且两台机器人的末端之间还存在着相对运动约束。双机器人协调焊接是典型的双机器人相对运动协调。

2　双机器人相对运动协调运动学分析

双机器人相对运动协调是指在任务过程中，两机器人相互协调完成任务，并且两机器人末端存在相对运动。

2.1相对运动协调坐标系的建立

在双机器人相对运动协调系统中的两台机器人中，一台为搬运机器人，负责搬运工件；另一台为工作机器人，携带工具，负责对工件进行焊接，写字等操作。通常定义搬运机器人为主机器人，设其为1号机器人，并且假定双机器人系统的世界坐标系就是1号机器人的基坐标系；工作机器人为从机器人，设其为2号机器人。用i表示机器人代号，则i=1,2。[R]表示双机器人系统的基坐标系（世界坐标系），[Ri]表示第i号机器人的基坐标系。[Ei]表示i号机器人的末端坐标系，[Ti]表示i号机器人的工具坐标系，[u]为工件坐标系。各坐标系关系如图2所示。

2.2双机器人相对运动协调任务运动学分析

根据上述分析和坐标系关系图可知：

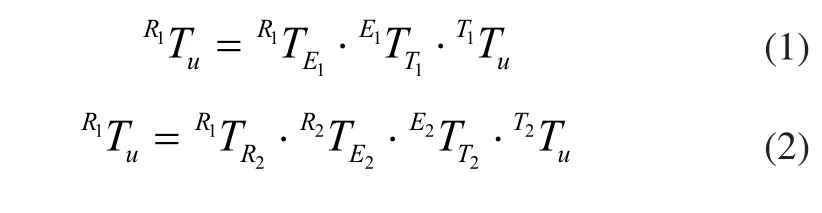
图2　双机器人相对运动协调任务中各坐标系的关系

对上述式(1)和式(2)进行变形，可以得到：

图3　双机器人系统仿真原理图

3　协调焊接任务运动学仿真

焊接领域是工业机器人应用最广的领域之一，但是对于复杂工件的焊接很多情况下还是依靠人工进行焊接，这是因为现有的焊接工作站所带有的变位机至多包含3个自由度，对于某些复杂的焊件，变位机与机器人组成的焊接工作站是无法完成焊接的。而由双机器人系统组成的焊接工作站则可以利用其强大的工作能力来完成复杂焊件的焊接。下面以双机器人协调焊接为例，对双机器人相对运动协调的运动学分析进行仿真验证。

待焊接的焊缝为如图4所示的相贯线，图中竖直放置的圆柱半径为r，水平放置的圆柱半径为R，在上图的中心点（蓝色的点）处建立工件坐标系，如图5所示。

图4　待焊接的工件

图5　工件坐标系

那么焊缝的参数方程表示为：

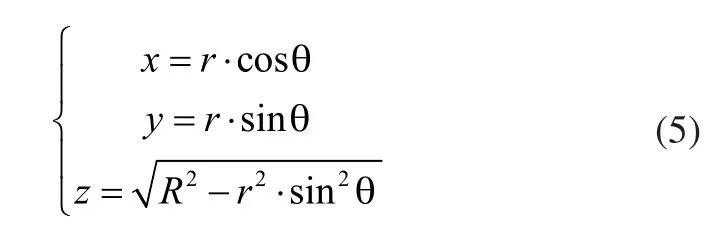
对于工件上的焊点来说，位置已经确定。为确定姿态，需建立焊点坐标系。以在该点处的切向量为x轴方向，方向向量为以两个曲面的法线所形成的角度的角平分线为z轴方向，方向向量为y轴方向向量由得到，这样便可以建立焊接点坐标系，并得到焊点坐标系在工件坐标系下的变换矩阵为：

为了获得较好的焊接效果，在此处选择船型焊进行焊接。船型焊要求焊缝的法线方向竖直向上，这样可以形成良好的焊接效果。那么要求焊点坐标系的z轴必须竖直向上，因此焊点坐标系与1号机器人基坐标系的z轴方向一致。根据现有条件是无法确定的，因此考虑加入一些人为的要求，所加的要求如下：

1）工件坐标系在机器人基坐标系下的位置保持不变，但是姿态可变，也就是说的位置向量保持不变。

2）被焊接点的焊接点坐标系与机器人基坐标系除了z轴方向一致之外，在这里要求其x方向与机器人基坐标系的y轴方向一致，据此来确定焊接点在世界坐标系下的姿态。

根据式(6)可知：

在式(7)中，Pp和P分别表示焊接点在世界坐标系下，在工件坐标系下的位置向量；Pu表示工件在世界坐标系下的位置向量，由于要求1）的存在，该向量为一个人为指定的常向量。利用式(7)便可获得焊接点在世界坐标系下的位置向量，那么焊接点在世界坐标系下的位姿矩阵为：

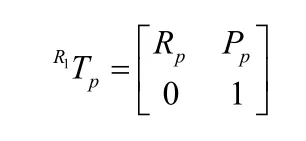
对于2号机器人来说，有如下关系式：

在仿真中我们指定工件坐标系在世界坐标系下的位置向量为：

1）对于1号机器人来说：

图6　焊接任务1号机器人仿真结果

从仿真结果来看，1号机器人对于路径上的各个点均可达，而且运动过程中各个关节变换平稳，未出现尖点，在任务过程中，机器人的灵活性较高，最小值为0.2252。

2）对于2号机器人来说：

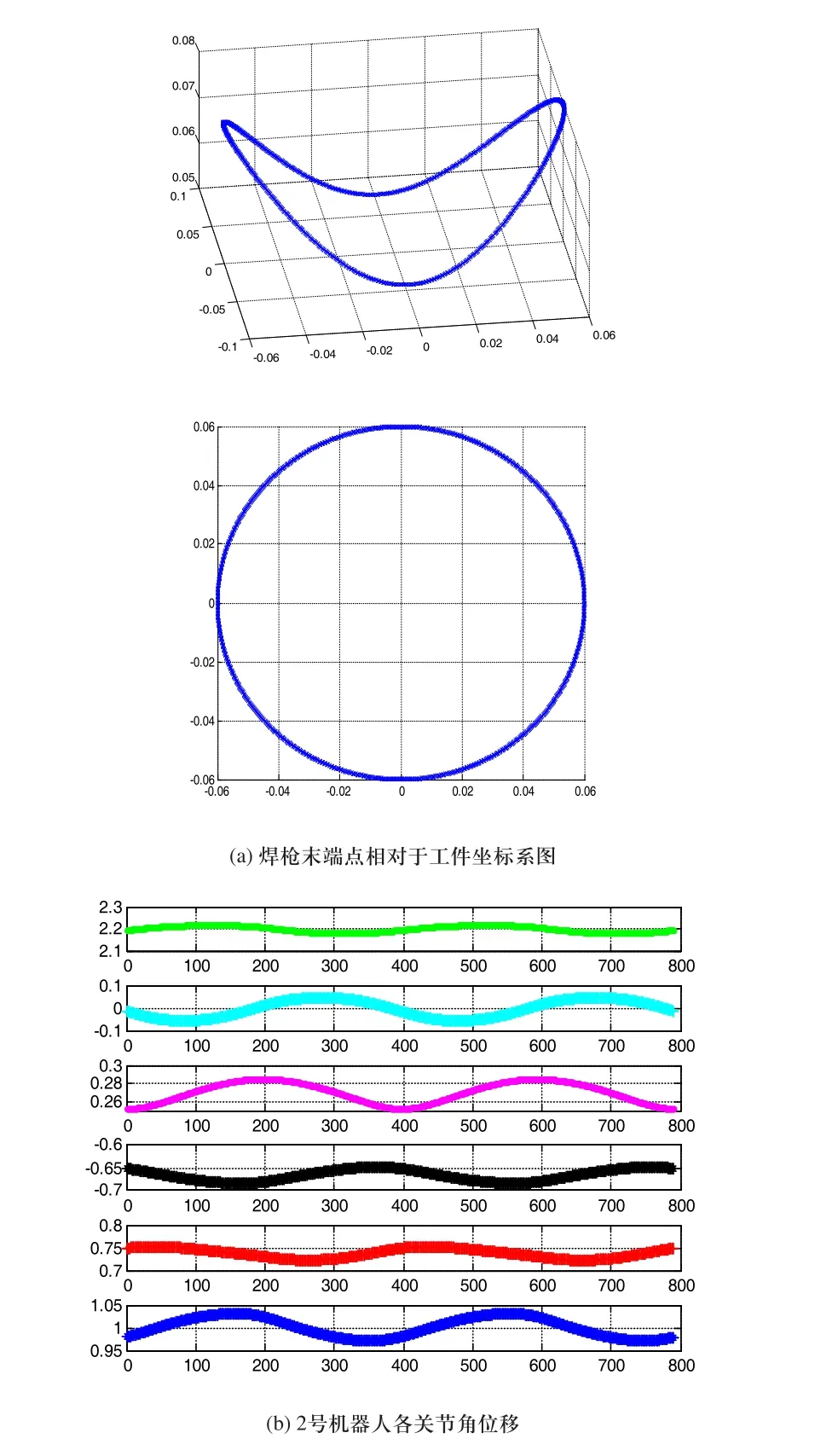
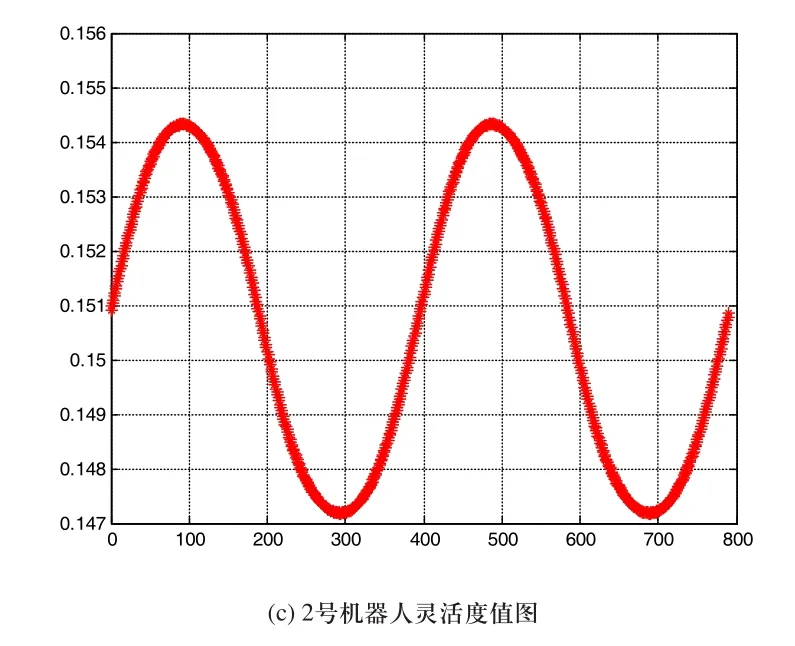
图7　焊接任务2号机器人仿真结果

从仿真结果来看，2号机器人对于路径上的各个点均可达，而且运动过程中各个关节变换平稳，未出现尖点，在任务过程中，机器人的灵活性较高，最小值为0.1472。从上述仿真中可以发现，两机器人可以完成协调焊接任务，而且在焊接过程中两机器人的关节角度变化平滑，灵活度值较高，证明了前述运动学分析的正确性。

4　结论

本文将双机器人协调分为双机器人同步运动协调和双机器人相对运动协调，并针对焊接任务对双机器人相对运动协调进行了运动学分析，并进行了仿真验证，仿真结果表明所分析的双机器人相对运动协调运动学关系的正确性。

[1] 宋韬.双工业机器人协调作业的研究[J].现代制造工程,2011,06:25-28.

[2] 石磊,史承权.双机器人协调操作的建模与仿真[J].煤矿机械,2012,04:82-83.

[3] 刘成良,张凯,Jay Lee.双机器人协调作业下碰撞算法及仿真研究[J].机器人,2003,02:167-171.

[4] 李平,张贤明,陈彬.双机器人系统的协调轨迹规划问题研究[J].现代制造工程,2013,11:25-29.

[5] Balletti L, Rocchi A,Belo F, et al. Towards variable impedance assembly: the VSA peg-in-hole[A].Humanoid Robots(Humanoids),2012 12th IEEE-RAS International Conference. IEEE[C].2012:402-408.

[6] 陈国良,黄心汉,王敏.平面复杂边缘的双机器人协调跟踪运动规划研究[J].控制与决策,2005,12:1374-1378.

[7] Hemmerlet J S, Prinz F B. Optimal path placement for kinematically redundant manipulators[A].Robotics and Automation,1991.Proceedings.,1991 IEEE International Conference. IEEE[C].1991:1234-1244.

[8] 孟庆鑫,李平,郭黎滨,王立权.多机器人协作技术分析及其实验系统设计[J].制造业自动化,2004,11:43-47.

[9] 欧阳帆.双机器人协调运动方法的研究[D].华南理工大学,2013.

[10] 张铁,欧阳帆.双机器人协调跟随运动的运动学分析与路径规划[J].上海交通大学学报,2013,08:1251-1256.

[11] 张华军.大厚板高强钢双面双弧焊新工艺及机器人自动化焊接技术[D].哈尔滨工业大学,2009.

[12] 杨光远.多层多道焊路径自动规划及双机器人协调研究[D].哈尔滨工业大学,2008.

The kinematics analysis of the dual-robot's coordination

YU Gang-dong, CHEN Qi

TP241.2

A

1009-0134(2016)02-0063-04

2015-11-24

于广东（1988 -），男，山东青岛人，硕士，研究方向为精密机械及机器人。